@Dmaxiya 2018-08-17T10:15:53.000000Z 字数 10607 阅读 979

Codeforces Round #502 (Div. 1 + Div. 2)

Codeforces

Contests 链接：Codeforces Round #502 (Div. 1 + Div. 2)
过题数：4
排名：765/7399

A. The Rank

题意

一个班上有 $n$ 个学生，每个学生都有一个 $id$ 和四门课的成绩，每个学生的 $id$ 为 $1$ 到 $n$ 之间的整数，每个学生的 $id$ 都不相同，将所有学生按总分从高到低排序，若总分相同则按 $id$ 从小到大排序，问 $id$ 为 $1$ 的学生最终排在第几名。

输入

第一行为一个整数 $n~(1\leq n\leq1000)$ ，接下去 $n$ 行每行 $4$ 个整数 $a_i,b_i,c_i,d_i~(0\leq a_i,b_i,c_i,d_i\leq100)$ ，第 $i$ 行的 $4$ 个整数表示 $id$ 号为 $i$ 的学生四门课的成绩。

输出

输出最终 $id$ 为 $1$ 的学生的排名。

样例

输入
5 100 98 100 100 100 100 100 100 100 100 99 99 90 99 90 100 100 98 60 99
输出
2
提示
$5$ 个学生的总分分别为 $398,400,398,379,357$ ， $id$ 为 $1$ 的学生的分数和 $id$ 为 $3$ 的分数相等，但是他的 $id$ 值更小，所以他排在第 $2$ 名。

输入
6 100 80 90 99 60 60 60 60 90 60 100 60 60 100 60 80 100 100 0 100 0 0 0 0
输出
1
提示
$6$ 个学生的总分分别为 $369,240,310,300,300,0$ ， $id$ 为 $1$ 的学生分数最高，所以他是第 $1$ 名。

题解

按照总分为主关键字， $id$ 为次关键字排序，然后 $O(n)$ 扫一遍找到 $id$ 为 $1$ 的学生的排名。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 1000 + 100;
struct Node {
    int sum, id;
};
bool operator<(const Node &a, const Node &b) {
    return a.sum == b.sum? a.id < b.id: a.sum > b.sum;
}
int n, num;
Node node[maxn];
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d", &n) != EOF) {
        for(int i = 1; i <= n; ++i) {
            node[i].sum = 0;
            node[i].id = i;
            for(int j = 0; j < 4; ++j) {
                scanf("%d", &num);
                node[i].sum += num;
            }
        }
        sort(node + 1, node + 1 + n);
        int ans = 0;
        for(int i = 1; i <= n; ++i) {
            if(node[i].id == 1) {
                ans = i;
                break;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

B. The Bits

题意

给定由 $n$ 个 $01$ 位组成的二进制数 $a$ 和 $b$ ，问对 $a$ 的所有 $01$ 位有多少种交换不同位的方式，使得 $a~or~b$ （按位或）的值发生改变。

输入

第一行为一个整数 $n~(2\leq n\leq10^5)$ ，第 $2$ 行为 $n$ 个 $01$ 字符，表示 $a$ 的所有二进制位，第 $3$ 行为 $n$ 个 $01$ 字符，表示 $b$ 的二进制位。

输出

输出方案数。

样例

输入
5 01011 11001
输出
4
提示
$a$ 中可以交换的 $01$ 位为： $(1,4),(2,3),(3,4),(3,5)$ 。

输入
6 011000 010011
输出
6
提示
$a$ 中可以交换的 $01$ 位为： $(1,2),(1,3),(2,4),(3,4),(3,5),(3,6)$ 。

题解

枚举所有 $a$ 和 $b$ 中 $01$ 位的对应情况：

$a$ 为 $0$ 的位对应的是 $b$ 为 $0$ 的位，与另一个 $a$ 为 $1$ 的位交换，当前位置上的或值将会从 $0$ 变为 $1$ ；

$a$ 为 $0$ 的位对应的是 $b$ 为 $1$ 的位，与另一个 $a$ 为 $1$ 而 $b$ 为 $0$ 的位交换，那么被交换的位置上的或值将会从 $1$ 变为 $0$ ；

$a$ 为 $1$ 的位对应的是 $b$ 为 $0$ 的位，与另一 $a$ 为 $0$ 的位交换，当前位置上的或值将会从 $1$ 变为 $0$ ；

$a$ 为 $1$ 的位对应的是 $b$ 为 $1$ 的位，与另一个 $a$ 为 $0$ 而 $b$ 为 $0$ 的位交换，被交换的位置上的或值将会从 $0$ 变为 $1$ 。

因此按照所有对应位置上 $ab$ 的 $01$ 状态求前缀和或者后缀和，最后 $O(n)$ 扫一遍就能得到答案。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100000 + 100;
int n;
int sum[maxn][4];
char a[maxn], b[maxn];
int id(int i) {
    return (a[i] - '0') * 2 +  b[i] - '0';
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d", &n) != EOF) {
        memset(sum, 0, sizeof(sum));
        scanf("%s%s", a + 1, b + 1);
        for(int i = n; i > 0; --i) {
            for(int j = 0; j < 4; ++j) {
                sum[i][j] = sum[i + 1][j];
            }
            ++sum[i][id(i)];
        }
        LL ans = 0;
        for(int i = 1; i < n; ++i) {
            switch(id(i)) {
                case 0: ans += sum[i + 1][2] + sum[i + 1][3]; break;
                case 1: ans += sum[i + 1][2]; break;
                case 2: ans += sum[i + 1][0] + sum[i + 1][1]; break;
                case 3: ans += sum[i + 1][0]; break;
                default: break;
            }
        }
        printf("%I64d\n", ans);
    }
    return 0;
}

C. The Phone Number

题意

构造一个 $1$ 到 $n$ 的排列，使得这个排列中最长上升子序列的长度加上最长下降子序列的长度最小。

输入

输入为一个整数 $n~(1\leq 10^5)$ 。

输出

输出 $n$ 个整数，为 $1$ 到 $n$ 的排列，如果有多解输出任意一组。

样例

输入
4
输出
3 4 1 2
提示
最长上升子序列的长度为 $2$ ，最长下降子序列的长度为 $2$ ，总和为 $4$ ，是所有排列中最小的，但不是唯一的答案。

输入
2
输出
2 1
提示
最长上升子序列的长度为 $1$ ，最长下降子序列的长度为 $2$ ，总和为 $3$ ，是所有排列中最小的，但不是唯一的答案，序列 $1~2$ 也是合法的答案。

题解

将 $n$ 分成 $m$ 块3，其中每一块中的数字是递增的，各个块之间是递减的，则最长上升子序列的长度和最长下降子序列的长度和最小，为 $m+\lceil\frac{n}{m}\rceil$ ，由基本不等式可知，当 $m$ 为 $\sqrt n$ 时 $m+\lceil\frac{n}{m}\rceil$ 的值最小。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100000 + 100;
int n;
int num[maxn];
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d", &n) != EOF) {
        int Index = sqrt(n);
        int tmp = 1;
        int Min = n;
        for(int i = n - Index; i >= 0; i -= Index) {
            Min = i;
            for(int j = 0; j < Index; ++j) {
                num[i + j] = tmp++;
            }
        }
        for(int i = 0; i < Min; ++i) {
            num[i] = tmp++;
        }
        for(int i = 0; i < n; ++i) {
            if(i != 0) {
                printf(" ");
            }
            printf("%d", num[i]);
        }
        printf("\n");
    }
    return 0;
}

D. The Wu

题意

有一个元素个数为 $m$ 的 $01$ 串集合，集合内的 $01$ 串可以重复出现，且每一个串的长度都为 $n$ ，对于两个 $01$ 串 $s$ 和 $t$ ，它们产生的价值为 $v_{s,t}=\sum_{i=1}^n(s_i==t_i?w_i:0)$ ，现在有 $q$ 次询问，每次询问由一个长度为 $n$ 的 $01$ 串 $s$ 和一个数 $k$ 组成，询问集合中满足条件 $v_{s,t}\leq k$ 的字符串个数。

输入

第一行为 $3$ 个整数 $n,m,q~(1\leq n\leq12,1\leq q,m\leq5\times10^5)$ 。第二行为 $n$ 个整数 $w_1,w_2,\cdots,w_n~(0\leq w_i\leq100)$ ，接下去 $m$ 行每行一个长度为 $n$ 的 $01$ 字符串，接下去 $q$ 行每行由一个长度为 $n$ 的 $01$ 字符串和 $k~(0\leq k\leq100)$ 组成。

输出

对于每次询问，输出答案。

样例

输入
2 4 5 40 20 01 01 10 11 00 20 00 40 11 20 11 40 11 60
输出
2 4 2 3 4

输入
1 2 4 100 0 1 0 0 0 100 1 0 1 100
输出
1 2 1 2

题解

先将字符串转化为对应数字（ $0$ 到 $2^n-1$ ），对于集合中的所有数字 $t$ ，统计每个数字出现的次数 $cnt_t$ ，接着对所有可能的询问 $s$ （ $0$ 到 $2^n-1$ ）都预处理出对应的价值 $v_{s,t}$ ，将价值为 $v_{s,t}$ 的集合中的数字 $t$ 的个数记录在 $sum[s][v_{s,t}]$ 中，即 $sum[s][v_{s,t}]=cnt_t$ ，由于询问中的 $k$ 最大值为 $100$ ，所以 $sum$ 数组的第 $2$ 维只需要开到 $100$ ，大于 $100$ 的可以不用处理，最后对 $sum$ 的每一次询问 $s$ 都做一遍前缀和，就能得到询问为 $s$ 时，价值小于等于 $k$ 的所有满足条件的 $t$ 的个数。预处理和查询的时间复杂度为 $O(m+2^n\times2^nn+100\times2^n+qn)$ 。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
int n, m, k, q;
char str[20];
int num[20], cnt[4096];
int sum[4096 + 100][100 + 20];
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d%d%d", &n, &m, &q) != EOF) {
        memset(cnt, 0, sizeof(cnt));
        memset(sum, 0, sizeof(sum));
        for(int i = 0; i < n; ++i) {
            scanf("%d", &num[i]);
        }
        for(int i = 0; i < m; ++i) {
            scanf("%s", str);
            int tmp = 0;
            for(int j = 0; j < n; ++j) {
                tmp |= (str[j] - '0') << j;
            }
            ++cnt[tmp];
        }
        for(int i = 0; i < (1 << n); ++i) {
            for(int j = 0; j < (1 << n); ++j) {
                int tmp = 0;
                for(int k = 0; k < n; ++k) {
                    if(((i >> k) & 1) == ((j >> k) & 1)) {
                        tmp += num[k];
                    }
                }
                if(tmp > 100) {
                    continue;
                }
                sum[i][tmp] += cnt[j];
            }
        }
        for(int i = 0; i < (1 << n); ++i) {
            for(int j = 1; j <= 100; ++j) {
                sum[i][j] += sum[i][j - 1];
            }
        }
        for(int i = 0; i < q; ++i) {
            scanf("%s%d", str, &k);
            int tmp = 0;
            for(int j = 0; j < n; ++j) {
                tmp |= (str[j] - '0') << j;
            }
            printf("%d\n", sum[tmp][k]);
        }
    }
    return 0;
}

E. The Supersonic Rocket

题意

有两个点集，点的个数分别为 $n$ 和 $m$ ，问两个点集分别构成的凸包是否可以通过旋转、平移使得两个凸包完全重合。

输入

第一行包含两个整数 $n,m~(3\leq n,m\leq10^5)$ ，接下去 $n$ 行每行两个整数 $x_i,y_i$ ，表示第一个点集中每个点的坐标，最后 $m$ 行每行两个整数 $x_i,y_i$ ，表示第二个点集中每个点的坐标，其中 $0\leq x_i,y_i\leq10^8$ 。

输出

如果可以通过旋转与平移使两个凸包完全重合，输出 $YES$ ，否则输出 $NO$ ，大小写任意。

样例

输入
3 4 0 0 0 2 2 0 0 2 2 2 2 0 1 1
输出
YES
提示
点集在平面直角坐标系上的位置为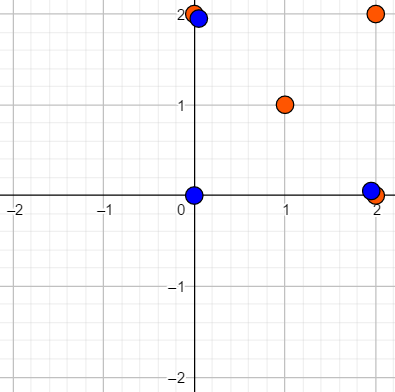：将第一个点集旋转 $1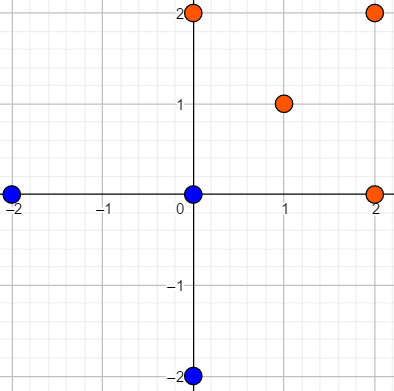80°$ 后：再将第二个点集平移 $(-2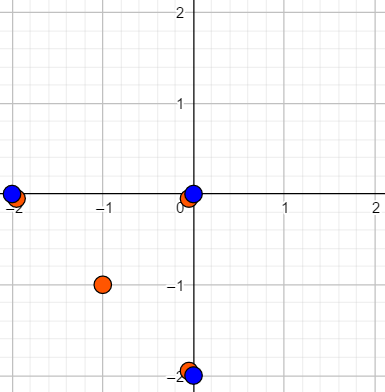,-2)$ 后：

输入
3 4 0 0 0 2 2 0 0 2 2 2 2 0 0 0
输出
NO
提示
不论如何平移旋转，两个凸包都不会重合。

题解

先分别跑出两个点集的凸包，判定两个凸包可以旋转平移重合的条件是：每条对应边的长度相等且对应角的大小相等，对应边直接求边长平方，对应角可以用叉积。将其中一个点集在凸包上所有点都复制到最后，让另一个凸包的所有点在这上面跑一遍 $kmp$ ， $kmp$ 能够往后跑的条件就是对应边与对应角都相等。

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
const int maxn = 100000 + 100;
struct Point {
    LL x, y;
    Point() {}
    Point(LL xx, LL yy) {
        x = xx;
        y = yy;
    }
};
LL operator*(const Point &a, const Point &b) {
    return a.x * b.x + a.y * b.y;
}
bool operator<(const Point &a, const Point &b) {
    return a.x == b.x? a.y < b.y: a.x < b.x;
}
LL operator^(const Point &a, const Point &b) {
    return a.x * b.y - a.y * b.x;
}
Point operator-(const Point &a, const Point &b) {
    return Point(a.x - b.x, a.y - b.y);
}
struct Cross_len {
    LL cross, len;
};
bool operator==(const Cross_len &a, const Cross_len &b) {
    return a.cross == b.cross && a.len == b.len;
}
bool operator!=(const Cross_len &a, const Cross_len &b) {
    return !(a == b);
}
int n[2], top[2];
Point point[2][maxn], sta[2][maxn << 1];
int Next[maxn];
Cross_len cross_len[2][maxn << 1];
void ConvexHull(Point *p, int n, int &top, Point *sta) {
    top = 0;
    sort(p + 1, p + 1 + n);
    for(int i = 1; i <= n; ++i) {
        while(top > 1 && ((sta[top - 1] - sta[top - 2]) ^ (p[i] - sta[top - 2])) <= 0) {
            --top;
        }
        sta[top++] = p[i];
    }
    int ttop = top;
    for(int i = n; i > 0; --i) {
        while(top > ttop && ((sta[top - 1] - sta[top - 2]) ^ (p[i] - sta[top - 2])) <= 0) {
            --top;
        }
        sta[top++] = p[i];
    }
    --top;
}
void Change_to_Cross_len(Point *p, int n, Cross_len *c) {
    Point p0 = p[0];
    for(int i = 0; i < n - 1; ++i) {
        p[i] = p[i + 1] - p[i];
        c[i].len = p[i] * p[i];
    }
    p[n - 1] = p0 - p[n - 1];
    c[n - 1].len = p[n - 1] * p[n - 1];
    for(int i = 0; i < n; ++i) {
        c[i].cross = p[i] ^ p[(i + 1) % n];
    }
}
void get_next(Cross_len *str, int n) {
    int j = -1;
    Next[0] = -1;
    for(int i = 1; i < n; ++i) {
        while(j != -1 && str[j + 1] != str[i]) {
            j = Next[j];
        }
        if(str[i] == str[j + 1]) {
            ++j;
        }
        Next[i] = j;
    }
}
bool kmp(Cross_len *str1, int n, Cross_len *str2, int m) {
    int j = -1;
    for(int i = 0; i < n; ++i) {
        while(j != -1 && str1[i] != str2[j + 1]) {
            j = Next[j];
        }
        if(str1[i] == str2[j + 1]) {
            ++j;
        }
        if(j == m - 1) {
            return true;
        }
    }
    return false;
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(scanf("%d%d", &n[0], &n[1]) != EOF) {
        memset(point, 0, sizeof(point));
        for(int i = 0; i < 2; ++i) {
            for(int j = 1; j <= n[i]; ++j) {
                scanf("%I64d%I64d", &point[i][j].x, &point[i][j].y);
            }
            ConvexHull(point[i], n[i], top[i], sta[i]);
            if(i == 0) {
                for(int j = 0; j < top[i]; ++j) {
                    sta[i][j + top[i]] = sta[i][j];
                }
                top[i] *= 2;
            }
            Change_to_Cross_len(sta[i], top[i], cross_len[i]);
        }
        get_next(cross_len[1], top[1]);
        if(kmp(cross_len[0], top[0], cross_len[1], top[1])) {
            printf("Yes\n");
        } else {
            printf("No\n");
        }
    }
    return 0;
}

F. The Neutral Zone

题意

注意本题内存限制为 $16MB$ 。
定义函数：

$f(x)=Ax^3+Bx^2+Cx+D\\ exlog_f(1)=0\\ exlog_f(p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k})=a_1f(p_1)+a_2f(p_2)+\cdots a_kf(p_k)$ 设 $n=p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}$ ，其中的每个 $p$ 是 $n$ 的质因数， $a$ 值是质因数对应的指数。
给定整数 $n$ 和参数 $A,B,C,D$ 的值，计算以下公式：

$\sum_{i=1}^nexlog_f(i)$

输入

输入包含 $4$ 个整数 $n,A,B,C,D~(1\leq n\leq3\times10^8,0\leq A,B,C,D\leq10^6)$ 。

输出

将计算结果对 $2^{32}$ 取模后输出。

样例

输入
12 0 0 1 0
输出
63

输入
4 1 2 3 4
输出
136

题解

从 $1$ 到 $n$ 内每个质数 $p$ 对答案的贡献为 $\lfloor\frac{n}{p}\rfloor+\lfloor\frac{n}{p^2}\rfloor+\cdots\lfloor\frac{n}{p^k}\rfloor$ ，其中 $k$ 为满足 $p^k\leq n$ 的最大值，因此最后的答案就是：

$\sum_{i=1}^nf(p_i)(\lfloor\frac{n}{p_i}\rfloor+\lfloor\frac{n}{p_i^2}\rfloor+\cdots\lfloor\frac{n}{p_i^k}\rfloor)$ 对 $2^{32}$ 取模，就是用 unsigned int 进行计算并让它们自然溢出。
最后是内存限制，如果我们用一个线性筛，就需要存每个数字是否是质数，如果用 bool 数组， $3\times10^8$ 的 bool 数组需要 $286MB$ ，用 bitset 压位需要 $\frac{286}{8}\approx35.75MB$ ，如果用埃氏筛，就可以在筛的过程中跳过 $2$ 和 $3$ 的倍数，我们将删去 $2$ 和 $3$ 的倍数后连续的数字用对应的 $1,2,...,n$ 表示：

$5$ $7$ $11$ $13$ $17$ $19$ $23$ $25$ $29$ $31$ $35$ $\cdots$

$1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$ $9$ $10$ $11$ $\cdots$

可以发现数字与下标之间是 $Index=\lfloor\frac{n}{3}\rfloor$ 的关系，因此如果跳过 $2$ 和 $3$ 的倍数，可以减少 $\frac{2}{3}$ 的空间，最后只需要 $\frac{35.75}{3}\approx11.9MB$ 。

$5$	$7$	$11$	$13$	$17$	$19$	$23$	$25$	$29$	$31$	$35$	$\cdots$
$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$	$\cdots$

过题代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <cstring>
#include <string>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <functional>
#include <iomanip>
using namespace std;
#define LL long long
unsigned n, a, b, c, d;
unsigned ans;
bitset<100000001> bit;
unsigned f(unsigned x) {
    return a * x * x * x + b * x * x + c * x + d;
}
unsigned Get(unsigned x) {
    unsigned ret = f(x);
    unsigned tmp = 0;
    for(unsigned i = 1; i <= n / x; i *= x) {
        tmp += n / (i * x);
    }
    return ret * tmp;
}
int main() {
    #ifdef LOCAL
    freopen("test.txt", "r", stdin);
//    freopen("test1.out", "w", stdout);
    #endif // LOCAL
    ios::sync_with_stdio(false);
    while(cin >> n >> a >> b >> c >> d) {
        ans = Get(2) + Get(3);
        bit.reset();
        for(unsigned i = 5; i <= n; ++i) {
            if(i % 2 == 0 || i % 3 == 0) {
                continue;
            }
            if(bit[i / 3] == 0) {
                ans += Get(i);
                for(unsigned j = i; j <= n / i; ++j) {
                    if(i * j % 2 == 0 || i * j % 3 == 0) {
                        continue;
                    }
                    bit[i * j / 3] = 1;
                }
            }
        }
        cout << ans << endl;
    }
    return 0;
}

Codeforces Round #502 (Div. 1 + Div. 2)

A. The Rank

题意

输入

输出

样例

题解

过题代码

B. The Bits

题意

输入

输出

样例

题解

过题代码

C. The Phone Number

题意

输入

输出

样例

题解

过题代码

D. The Wu

题意

输入

输出

样例

题解

过题代码

E. The Supersonic Rocket

题意

输入

输出

样例

题解

过题代码

F. The Neutral Zone

题意

输入

输出

样例

题解

过题代码

内容目录