@Dmaxiya
2018-08-17T02:24:56.000000Z
字数 6466
阅读 1629
Codeforces Round #492 (Div. 1)
Codeforces
Contests 链接:Codeforces Round #492 (Div. 1)
过题数:1
排名:409/663
A. Tesla
题意
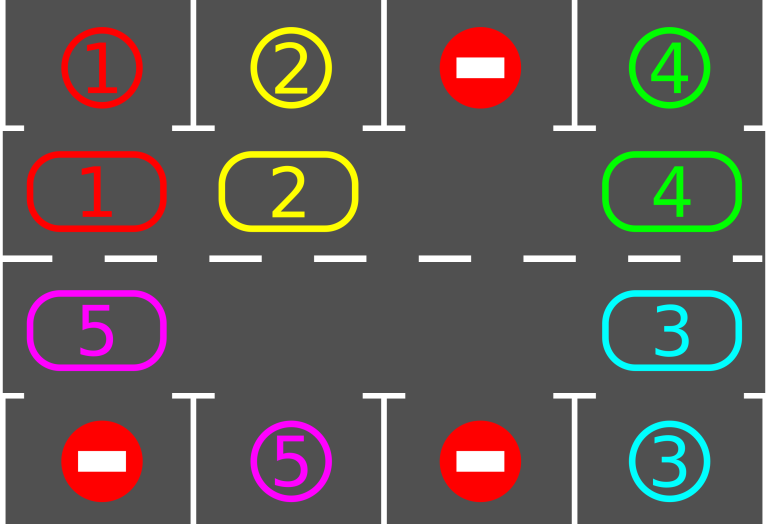
在一个 停车场上,第 行和第 行是停车位,第 行和第 行是车行道,如下图:
总共有 辆车,分别编号为 到 ,每辆车都要停到与车辆编号相同的停车位上。每辆车每次只能移动到相邻的坐标上,且编号为 的车辆只允许在车行道上行驶或者进入编号为 的停车位内,不允许进入其他编号的停车位与没有编号的停车位上。问是否能找到一种移动次数在 次内的车辆行驶方案,使得所有车都进入到对应的停车位,如果可以,则输出车辆行驶路线,否则输出 。
输入
第一行包括两个整数 和 ,接下去四行每行 个整数,第 行和第 行的非零数字表示对应编号的停车位, 表示禁止进入的停车位,第 行和第 行非零数字表示对应编号的车的位置, 表示空地,其他车辆可以移动到该处。
输出
如果无法在 步内将所有车辆移动到对应的停车位,则输出 ,否则第一行输出一个整数 表示需要的移动次数,接下去 行每行三个整数 ,表示第 辆车移动到第 行第 列的位置上,移动的位置必须保证合法。如果有多解则输出任意一组。
样例
| 输入 | 输出 | 提示 |
|---|---|---|
| 4 5 1 2 0 4 1 2 0 4 5 0 0 3 0 5 0 3 |
6 1 1 1 2 1 2 4 1 4 3 4 4 5 3 2 5 4 2 |
除了车辆 ,其他车辆都在相应的停车位旁,样例输出给出的是到达相应停车位的最快的方式, 其他任何一种移动次数小于 次的方案都是允许的。 |
| 1 2 1 2 1 2 |
-1 | 所有车辆都在一列内,且他们的相对位置导致它们无法回到自己的停车位内,所以只能输出 。 |
| 1 2 1 1 2 2 |
2 1 1 1 2 4 1 |
题解
可以将所有车辆按顺时针或者逆时针的顺序在第 、 行内移动,每次移动,检查车辆位置是否在对应停车位旁,如果是,则直接进入停车位,否则继续跟着所有车辆移动。可以计算得出,最坏情况下 所有车辆需要的移动次数为 ,如果无法顺/逆时针移动,车辆也无法进入停车位,则输出 。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <sstream>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <algorithm>using namespace std;#define LL long longconst int maxn = 500;const int maxcnt = 20000 + 100;struct Node {int x, y;Node() {}Node(int xx, int yy) {x = xx;y = yy;}};bool operator!=(const Node &a, const Node &b) {return a.x != b.x || a.y != b.y;}int n, k, anscnt, cnt;int num[4][maxn];Node pre[4][maxn];bool vis[4][maxn];int ans[maxcnt][3];const int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};bool in(int x, int y) {return x >= 1 && x <= 2 && y >= 0 && y < n;}void dfs(int x, int y) {for(int i = 0; i < 4; ++i) {int xx = x + dir[i][0];int yy = y + dir[i][1];if(in(xx, yy) && !vis[xx][yy]) {vis[xx][yy] = true;pre[xx][yy] = Node(x, y);dfs(xx, yy);}}}void get_in() {for(int i = 1; i <= 2; ++i) {for(int j = 0; j < n; ++j) {if(num[i][j] != 0 && num[i][j] == num[i ^ 1][j]) {ans[anscnt][0] = num[i][j];ans[anscnt][1] = (i ^ 1) + 1;ans[anscnt][2] = j + 1;anscnt++;num[i][j] = 0;--cnt;}}}}bool Go() {for(int i = 1; i <= 2; ++i) {for(int j = 0; j < n; ++j) {if(num[i][j] == 0) {Node Begin = Node(i, j);Node first = pre[Begin.x][Begin.y];Node second = Begin;while(first != Begin) {if(num[first.x][first.y] != 0) {ans[anscnt][0] = num[first.x][first.y];ans[anscnt][1] = second.x + 1;ans[anscnt][2] = second.y + 1;++anscnt;}swap(num[first.x][first.y], num[second.x][second.y]);second = first;first = pre[second.x][second.y];}return true;}}}return false;}int main() {#ifdef Dmaxiyafreopen("test.txt", "r", stdin);#endif // Dmaxiyaios::sync_with_stdio(false);while(scanf("%d%d", &n, &k) != EOF) {anscnt = 0;cnt = k;memset(vis, 0, sizeof(vis));for(int i = 0; i < 4; ++i) {for(int j = 0; j < n; ++j) {scanf("%d", &num[i][j]);}}dfs(1, 0);bool flag;do {get_in();flag = Go();} while(flag && cnt != 0);if(cnt != 0) {printf("-1\n");continue;}printf("%d\n", anscnt);for(int i = 0; i < anscnt; ++i) {for(int j = 0; j < 3; ++j) {if(j != 0) {printf(" ");}printf("%d", ans[i][j]);}printf("\n");}}return 0;}
B. Suit and Tie
题意
有 对夫妻,他们坐在一排,每对夫妻之间的位置不一定是相邻的,如果每次只能将相邻位置的两个人交换位置,问最少要交换多少次才能让所有夫妻坐在相邻的位置上。
输入
第一行为一个整数 ,第二行为 个整数 ,数据保证 到 的每个数字只出现 次。
输出
输出最少的交换次数。
样例
| 输入 | 输出 | 提示 |
|---|---|---|
| 4 1 1 2 3 3 2 4 4 |
2 | 可以通过下面的交换达到结果: ; 也可以通过下面的交换达到结果: 。 |
| 3 1 1 2 2 3 3 |
0 | 已经使得所有夫妻座位相邻,因此不需要进行任何交换。 |
| 3 3 1 2 3 1 2 |
3 |
题解
对于每个数字中在左边的那个,去找另一个数字,将另一个数字移动到左边的数字旁边, 依次贪心下去,就能得到最短的移动步数。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <sstream>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <algorithm>using namespace std;#define LL long longconst int maxn = 300;int n;int num[maxn];int Find(int Index, int x) {for(int i = Index; i <= n; ++i) {if(num[i] == x) {return i;}}return -1;}int main() {#ifdef Dmaxiyafreopen("test.txt", "r", stdin);#endif // Dmaxiyaios::sync_with_stdio(false);while(scanf("%d", &n) != EOF) {int ans = 0;n *= 2;for(int i = 1; i <= n; ++i) {scanf("%d", &num[i]);}for(int i = 1; i <= n; ++i) {int End = Find(i + 1, num[i]);if(End != -1) {for(int j = End - 1; j > i; --j) {swap(num[j], num[j + 1]);++ans;}}}printf("%d\n", ans);}return 0;}
C. Leaving the Bar
题意
给定 个向量,要求对每个向量分配一个系数 或 ,使得所有向量乘上对应的系数后相加得到的最终的向量模长不超过
输入
第一行包含一个整数 ,接下去 行每行两个整数 ,表示第 个向量的值 ,数据保证每一个向量的模长 。
输出
输出一行,包含 个整数 ,每个整数必须为 或 ,表示每个向量对应的系数,输出必须保证 。如果有多解输出任意一组即可。
样例
| 输入 | 输出 |
|---|---|
| 3 999999 0 0 999999 999999 0 |
1 1 -1 |
| 1 -824590 246031 |
1 |
| 8 -67761 603277 640586 -396671 46147 -122580 569609 -2112 400 914208 131792 309779 -850150 -486293 5272 721899 |
1 1 1 1 1 1 1 -1 |
题解
由如下断言:
对于任意三个模长小于 的向量 , 个向量中,两两之间夹角最小的角度最大为 ,将这两个夹角小于 的向量做差,则得到的新向量的长度一定不大于 。
可知,可以将 个向量每 个之间选择两个求和或做差,最终得到的向量模长一定不大于 ,合并到只剩下两个向量时,这两个向量所在的直线夹角最大为 ,将这两个向量求和或做差,得到的向量长度最大为 。
过题代码
#include <iostream>#include <cstdio>#include <cstdlib>#include <cmath>#include <sstream>#include <cstring>#include <string>#include <vector>#include <list>#include <queue>#include <stack>#include <map>#include <set>#include <algorithm>using namespace std;#define LL long longconst int maxn = 200000 + 100;struct Node {LL x, y;int l, r;Node() {}Node(LL xx, LL yy) {x = xx;y = yy;}double length() {return sqrt(x * x + y * y);}LL mult(const Node &n) {return x * n.x + y * n.y;}Node operator-() {return Node(-x, -y);}};LL operator*(const Node &a, const Node &b) {return a.x * b.y - a.y * b.x;}Node operator-(const Node &a, const Node &b) {return Node(a.x - b.x, a.y - b.y);}int n, cnt;int ans[maxn], the_Index[3];Node node[maxn];bool Close(Node &a, Node &b) {if(a.mult(b) < 0) {return false;}LL tmp = abs(a * b);return tmp <= a.length() * b.length() / 2 * sqrt(3.0);}int Creat_Node(const Node &n, int l, int r) {++cnt;node[cnt] = n;node[cnt].l = l;node[cnt].r = r;return cnt;}void Solve() {sort(the_Index, the_Index + 3);do {int l = the_Index[0];int r = the_Index[1];Node tmp = node[l];Node ntmp = node[r];if(Close(tmp, ntmp)) {ans[l] = 1;ans[r] = -1;int Index = Creat_Node(tmp - ntmp, l, r);ans[Index] = 1;the_Index[0] = Index;the_Index[1] = the_Index[2];return ;}ntmp = -node[r];if(Close(tmp, ntmp)) {ans[l] = ans[r] = 1;int Index = Creat_Node(tmp - ntmp, l, r);ans[Index] = 1;the_Index[0] = Index;the_Index[1] = the_Index[2];return ;}} while(next_permutation(the_Index, the_Index + 3));}int main() {#ifdef Dmaxiyafreopen("test.txt", "r", stdin);#endif // Dmaxiyaios::sync_with_stdio(false);while(scanf("%d", &n) != EOF) {cnt = 0;for(int i = 1; i <= n; ++i) {scanf("%I64d%I64d", &node[i].x, &node[i].y);node[i].l = node[i].r = 0;++cnt;}if(n == 1) {printf("1\n");continue;}ans[1] = 1;the_Index[0] = 1;the_Index[1] = 2;for(int i = 3; i <= n; ++i) {the_Index[2] = i;Solve();}int l = the_Index[0];int r = the_Index[1];if(node[l].mult(node[r]) >= 0) {ans[r] = -1;} else {ans[r] = 1;}for(int i = cnt; i >= 1; --i) {ans[node[i].l] *= ans[i];ans[node[i].r] *= ans[i];}for(int i = 1; i <= n; ++i) {if(i != 1) {printf(" ");}printf("%d", ans[i]);}printf("\n");}return 0;}