第十四讲 智能算法——模拟退火算法

数学建模 讲义 NUDT 2023SP

---

---

14.1 模拟退火算法的基本原理

• 模拟退火（Simulated Annealing, SA）算法是一种 模拟固体退火过程 的随机优化算法
• 最初的思想由 Nicholas Metropolis 于 1953 年提出，1983 年 Scott Kirkpatrick 借鉴了 Metropolis 的思想，将其应用于求解优化问题，发展出模拟退火算法
• Metropolis 和 Von Neumann、Ulam 是 Los Alamos 实验室的同事，对 Monte Carlo 做出了很多贡献

---

物理退火过程

• 固体加热到熔点后再冷却，冷却后固体的结构性质取决于冷却的速度
• 退火：即慢速冷却，能够使得固体内部的能量达到最低点，从而形成比较大的结构稳定的晶体
• 淬火：即快速冷却，难以达到内部能量的最低点，产生的结晶容易出现瑕疵

---

Metropolis 准则

粒子在温度 $T$ 时趋于平衡的概率为

$$\exp\left(-\dfrac{\Delta E}{kT}\right)$$

• $E$ 为温度 $T$ 时的内能
• $\Delta E$ 为内能的改变量
• $k$ 为 Boltzmann 常数

---

重要性采样法

• Metropolis 准则也称为 重要性采样法，即在寻找物理系统的热平衡状态时，以一定的概率接受新的状态
  
  • 在同一温度下，系统在可能的状态之间的转换，是以一定的概率发生的
  • 转换的概率取决于两个状态之间的能量差 $\Delta E$
• 转移概率：$P=\begin{cases} 1,& \Delta E<0 \\ \exp\left(-\dfrac{\Delta E}{T}\right), & \Delta E>0\end{cases}$
  
  • 相差一个 Boltzmann 常数，不影响下面的讨论.

---

状态的转移概率

$$P=\begin{cases} 1,& \Delta E<0 \\ \exp\left(-\dfrac{\Delta E}{T}\right), & \Delta E>0\end{cases}$$

• 当 $\Delta E<0$ 时，新状态的能量比原来状态的能量更低，应无条件接受新的状态
• 而如果新的状态比当前状态能量要高，也不是一概拒绝，而是以一定的概率来接受它
  
  • 能量差越大，接受新状态的概率越小
  • 当前温度越高，接受新状态的概率越大

---

转移的实现

$$\exp\left(-\frac{\Delta E}{T}\right)>r$$

• 其中 $r$ 是 $0\sim 1$ 之间的随机数
• 根据两个状态能量的差值，以及当前温度，计算出 $\exp\left(-\frac{\Delta E}{T}\right)$ 的值，然后与随机生成的数字进行比较
• 如果大于这个随机数，就接受新状态，如果小于这个随机数，则拒绝

---

14.2 模拟退火算法的步骤与要素

$$\boxed{\begin{array}{l|l} \text{物理退火} & \text{模拟退火} \\ \hline \text{状态} & \text{经过编码的可行解} \\ \text{能量} & \text{评价函数} \\ \text{温度} & \text{控制参数} \\ \text{状态转换} & \text{寻找邻近的可行解} \\ \text{Metropolis 准则} & \text{等温过程：在同一控制参数下，随机寻找最优解} \\ \text{温度降低/冷却} & \text{控制参数下降} \\ \end{array}}$$

---

名词解释

• 模拟退火算法中的解就是实际物理过程中粒子的状态，一般是以向量的形式对解进行编码，但是对于简单的问题，问题的解也可能就是一个实数，这是由问题本身决定的
• 最优解对应稳定的状态，或者说能量最低的状态
• 评价函数对应能量，是用于评价解的优劣的函数，与问题优化目标有关，但是不完全等价
• 为了与物理现象中的表述习惯一致，我们通常将评价函数设置成函数值越低的解越好
• 初始温度对应退火初始的状态
• 邻近解指的是转换的状态，是在一个什么样的邻域范围内进行转化，从而产生一个新解
• 新解产生的方式一般是在当前解的邻域内，对当前解增加一些扰动，随机寻找一个新的解
  
  • 参考遗传算法中产生解的那些方式，类似于变异、交叉这些操作，因为变异和交叉在某种意义下，都可以理解为某种随机的扰动
• Metropolis 采样过程是一个等温的过程，是在同一温度下，随机寻找更优解的过程
• 控制参数下降，即温度下降，对应物理上的冷却过程

---

算法框架

• 设定初始状态、运行参数与初始解
• 循环（退火）：直到系统冷却到指定的状态
  
  • 循环（等温）：直到满足一定的终止条件
    
    • 生成新的邻近解
    • 对新生成的解进行评价
    • 接受或舍弃新生成的解
  • 降温

---

影响模拟退火算法效果的因素

• 初始温度与初始解
• 三个函数
  
  • 状态生成函数，即生成新解的方式
  • 状态选择函数，一般用 Metropolis 准则进行选择，也可以设计其他选择方式
  • 温度控制函数，或者说降温策略
• 两个条件：内外循环的终止条件
• 各因素往往有一定的关联，需要在设计算法的时候综合考虑

---

1. 初始温度的设置

• 初始温度必须足够高，以保证可能搜索到整个可行域，否则算法会退化成爬山法
  
  • 初始温度越高，搜索到全局最优解的可能性越大，但是计算时间也会越长
    
    • 初始温度如果太高，在算法运行的初期将等效于随机搜索，严重影响算法的效率
  • 初始温度较低，能够节约时间，但是全局搜索性能会下降
• 初温的设置没有通用的方法，一般需要根据实际问题和实验结果进行调整

---

设置初温的常用方法

1. 随机产生一组状态，确定两两状态之间评价函数值差的最大值 $|\Delta_{\max}|$，再利用一定的函数确定初温
   
   • 例如，$T_0=|\Delta_{\max}|/p_r$，其中 $p_r$ 为初始接受概率
2. 开始设置一个非常高的温度，然后快速降温，一直到效果较差的解的接受概率接近 60% 时停止，然后将该温度作为正式的初温，开始缓慢的退火过程
3. 均匀抽取一组状态，以各状态评价函数值的方差作为初温

---

2. 退火方式（温度管理）

• 退火方式的选择是设计一个模拟退火算法的难点之一
• 理论上，在每一个温度都要迭代足够多次，才能达到该温度下的稳态，但是随着迭代次数的增加，求解的速度会变得非常慢，因此必须折衷
  
  • 可以取比较少的温度值，每一温度值下面的迭代次数多一点（即外层循环少，内层循环多）
  • 或者是温度值取的比较多，每一温度值下的迭代次数少一些（即外层循环多，内层循环少）
• 没有固定的方法用于选择退火方式，而是需要根据实验结果和具体的问题来确定

---

常用退火方式

• 线性退火方式 $T(t+1)=T(t)-\Delta T$
• 指数退火方式 $T(t+1)=\alpha T(t),\quad\alpha\in(0,1)$
  
  • $\alpha$ 一般介于 0.8 至 0.99 之间，$\alpha$ 越大，退火速度越慢，达到外循环停止条件的时间越长
• 经典退火方式 $T(t)=\frac{T_0}{\ln(t+1)}$
  
  • 温度下降较慢，因此算法收敛速度也很慢
• 快速退火方式 $T(t)=\frac{T_0}{1+\alpha t}$
  
  • 高温区退火速度较快，在低温区退火速度逐渐变慢，因此算法在低温区迭代的次数相对较多，更有可能搜索到最优解

---

3. 内循环的停止条件

内循环的停止条件决定了在每一温度下的迭代次数

• 方法一：将每一温度下的循环次数设置为常数
• 方法二：在每一个温度下只计算一次，但是温度的下降（外循环）速度非常慢
  
  • 例如：$T(t+1)=\frac{T(t)}{1+\beta T(t)}$，其中 $\beta$ 是一个非常小的常数
• 方法三：动态调整内循环次数，高温时循环次数少一些，低温时循环次数多一些

---

4. 外循环停止条件（终温的设置）

• 通常可以使最终温度降到 0，也就是一直要降到 $T=0$ 时才停止
  
  • 有利于保证收敛性，但运行时间往往过长，计算代价很高
• 根据 Metropolis 准则，当温度非常接近 0 时，差解的接受概率已经非常接近 0，不需要等 $T$ 降到 0 时才停止
• 常见的停止条件：
  
  1. 一个合适的较低的温度
  2. 系统进入稳态，即既没有好解也没有坏解被接受
  3. 确定的迭代次数

---

5. 评价函数

• 与遗传算法中适应度函数类似，评价函数在模拟退火算法中也很重要
• 由于每次迭代都要计算一次评价函数，而且对于实际问题，评价函数往往很复杂，计算费时，所以要尽可能设计高效的评价函数
  
  • 考虑到算法只关心能量的差值，所以可以直接计算评价函数的差值，前提是计算差值比较简便
  • 或者对评价函数进行简化，只要能说明优劣即可
• 评价函数的区分度要尽可能好

---

示例

$$\boxed{\begin{array}{c|cc} \Delta E & T=100 & T=10 \\ \hline 10 & 0.90483742 & 0.36786744 \\ 20 & 0.81873075 & 0.13533528 \\ 30 & 0.74081822 & 0.04978707 \\ 40 & 0.67032005 & 0.01831564 \\ 50 & 0.60653066 & 0.00673795 \\ \cdots & \cdots & \cdots \\ 200 & 0.13533528 & 2.0612\times 10^{-19} \end{array}}$$

---

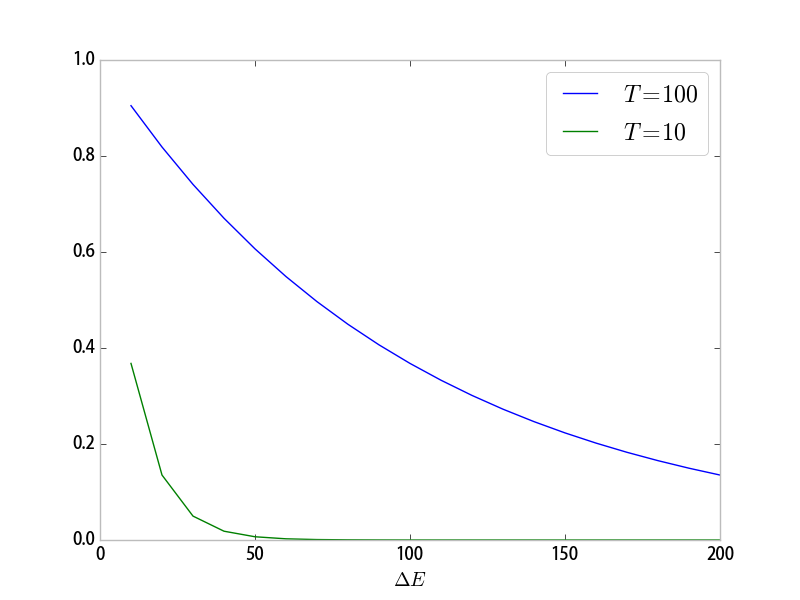
性能分析

• 新状态接受概率是由系统的温度和评价函数值的差决定
• 对于同样的温度，能量差越大接受的概率越小
• 对于相同的能量差，温度越高，接受的概率越大，温度越低，接受的概率越小
• 极端的情况，若 $T=0$，则表示不接受任何比当前情况更差的结果，算法就会退化成爬山法

---

6. 初始解的选取

• 一般可以随机选取初始解，算法的收敛性不依赖于初始解的选取
• 但是从一个好的近似解出发，求解效果会更好
• 比如 TSP 问题，先用贪心法得到一个近似解作为初始解，可以提高求解效率

---

7. 接受概率

• 一般使用 Metropolis 准则，但是指数运算比较费时间，针对特定问题，使用其他形式可能效率更高
• 例如：$P=1-\dfrac{\Delta E}{T}$
  
  • 在基本保持解的质量的前提下，提高算法计算效率

---

14.3 模拟退火算法的应用

1. 求函数的最值
2. 十滴水游戏
3. 求解 TSP 问题

---

1. 求函数的最值

求函数

$$f(x)=x\sin(10\pi x)+2$$

在区间 $[-1,2]$ 上的最大值

---

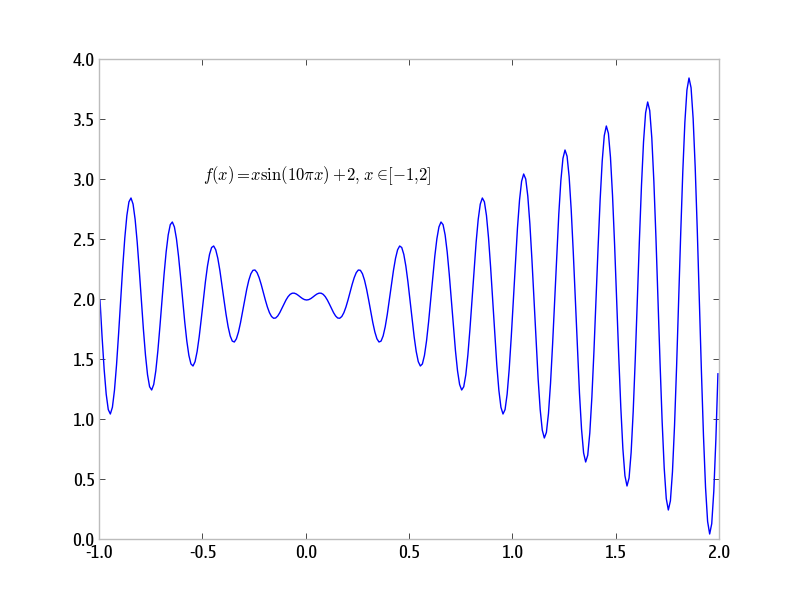
分析

• 与模拟退火算法常用的表述习惯一致，我们考虑 $-f(x)$ 在区间 $[-1,2]$上的最小值问题
• 问题的解是区间 $[-1,2]$ 上的实数，用浮点数对解进行编码
• 使用目标函数 $-f(x)$ 作为评价函数
• 产生新解时，可以设定一个最大扰动量 $\delta$，在当前解的 $\delta$ 邻域内随机寻找一个点作为新解

---

参数选取

• 初温取 70，终温取 0.1
• 采用指数退火方式，退火系数 0.99
• 使用 Metropolis 准则进行选择
• 在每个温度下，内循环只执行一次

---

计算结果

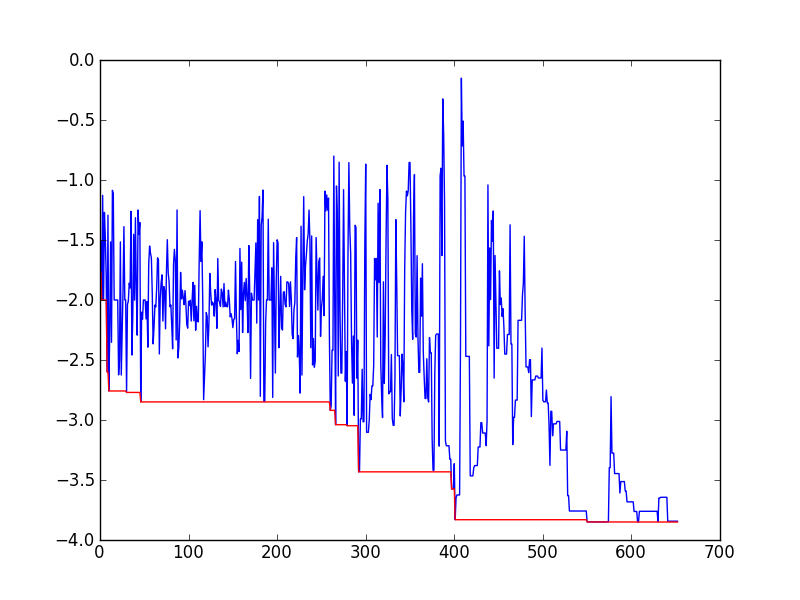
• 最优解：$x^*=1.850736$，函数最大值 $f(x^*)=3.850241$，解的精度比较高
• 与遗传算法相比，模拟退火不涉及种群的演化，算法上更容易实现，但是需要调整和设计的参数更多

---

2. 十滴水游戏

• 与上一节中类似，只考虑游戏的基本规则，即，对于给定的游戏开局，求解过关策略，使得过关所用的水滴最小（点击次数最少），不考虑奖励的水滴和积分
• 仍然可以用一个点击序列表示一个解，给定一个点击序列，通过模拟点击，容易判断它的优劣

---

解的编码

• 使用一个 $6\times 6$ 的矩阵 $\boldsymbol{A}$ 记录当前的盘面信息，每个元素 $a_{ij}$ 是取值为0--4的整数，表示在第 $i$ 行，第 $j$ 列的位置，有一个包含 $a_{ij}$ 滴水的水滴
• 向第 $i$ 行，第 $j$ 列的格子增加一滴水（点击一次）的单次点击可以记为 $(i,j)$，其中 $1\leqslant i,j \leqslant 6$，或者记为两位十进制数 $ij$
• $l$ 次点击序列可以记为长度为$l$的一个向量：$\boldsymbol{c}=[(i_1, j_1),(i_2, j_2),\ldots,(i_l, j_l)]$ 或 $\boldsymbol{c}=[i_1 j_1, i_2 j_2, \ldots, i_l j_l]$

---

评价函数

• 对于给定的一个点击序列，即长度为 $l$ 的向量 $\boldsymbol{c}$，按照点击序列的顺序，依次模拟每次点击后盘面的变化情况，最终可能出现的情况只有以下两种：
  
  • 依次点击 $k$ 次（$k\leqslant l$）后，盘面被清空；
  • 依次点击 $l$ 次后，盘面上仍然剩余 $r$ 个水珠
• 对于第一种情况，显然 $k$ 越小越好，对于第二种情况，一般来说，可以近似认为 $r$ 越小越好

---

构造评价函数

$$f(\boldsymbol{c})=\left\{ \begin{array}{ll} k, & \mbox{情况1} \\ l+r, & \mbox{情况2} \end{array} \right.$$

• $f$ 的取值为 1 到 $l+36$ 之间所有的整数
• $f$ 的值越少，对应的解越好
• 当出现情况 2 时，$f$ 的取值有缺陷，可以通过增大 $l$ 来解决
• 形式上，与遗传算法中所用的适应度函数有区别，如果直接取$-f(x)$也可以

---

新解的产生

• 产生新解的方法类似遗传算法中的变异算子
• 随机选定当前解中的某一次点击，随机用盘面上其他位置代替，可以只选择还有水珠的那些格子
• 对于评价函数值 $k$ 已经小于 $l$ 的解，以上操作可以只在前$k$个位置进行
• 如果找到评价函数值为 1 的解，算法可以停止

---

参数与结果

• 初温取 60，终温取 0.1，指数退火方式，退火系数 0.99
• 使用 Metropolis 准则确定接受概率
• 内循环次数取 10
• 针对这一开局，求得最优解需要两次点击 (3, 3), (3,3)
  （0--5编码）

---

算法性能

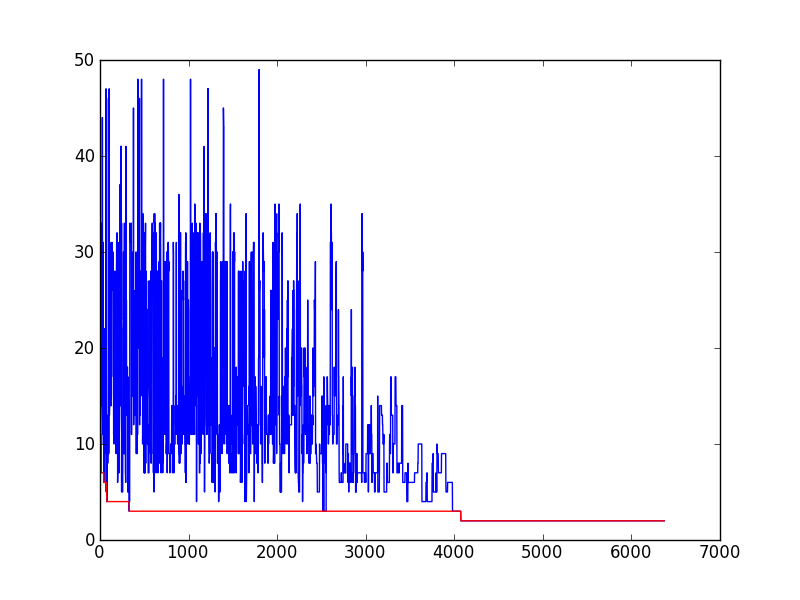
• 可以看出，收敛速度比较快
• 可能的改进：
  
  • 尝试使用其他方法生成新的解
  • 调整模拟退火算法中的其他参数

---

3. 旅行商问题

• Travelling Salesman Problem (TSP)，中文称为货郎担问题或旅行商问题
• 设有 $n$ 个城市，用 $1,2,\ldots,n$ 表示，城市 $i$ 和城市 $j$ 之间的距离为 $d(i,j)$，$(i,j=1,2,\ldots,n)$
• TSP 问题是要找到访问每个城市恰好一次的一条回路，且其路径总长度为最短

---

解空间与初始解

• 解空间 $S$ 是遍访每个城市恰好一次的所有回路，是 ${1,2,\ldots,n}$ 的所有循环排列的集合，
  
  • $S=\{(\pi_1,\pi_2,\ldots,\pi_n)|(\pi_1,\pi_2,\ldots,\pi_n)\mbox{为}(1,2,\ldots,n)\mbox{的排列}\}$
  • $\pi_i=j$ 表示在第 $i$ 次访问第 $j$ 个城市
  • 记 $\pi_{n+1}=\pi_1$
• 初始解：$(1,2,\ldots,n)$

---

评价函数

• 评价函数定义为路径的总长度
• $f(\pi_1,\pi_2,\ldots,\pi_n)=\sum_{i=1}^n d(\pi_i,\pi_{i+1})$
  
  • $(\pi_1,\pi_2,\ldots,\pi_n)\in S$
  • $\pi_{n+1}=\pi_1$

---

新解的产生

可以单独或混合使用以下的方法：

1. 2 变换法：随机生成下标 $i, j \;(i < j)$，交换两个下标所对应城市的位置
2. 3 变换法：随机生成下标 $i, j , k \; (i < j < k )$，将 $\pi_i$, $\pi_j$ 之间的路径插入到 $\pi_k$ 之后
3. 逆转中间/两端变换法 随机生成下标 $i$, $j$，
   
   • 若 $i < j$，则逆转 $\pi_i$ 到 $\pi_j$ 之间的路径
   • 若 $i > j$，则逆转 $\pi_i$ 之后与 $\pi_j$ 之前的路径

---

接受概率

$$P=\left\{\begin{array}{ll} 1, & \Delta f<0, \\ \exp\left(-\dfrac{\Delta f}{bT}\right), & \Delta f\geqslant 0. \end{array}\right.$$

• 为简单计，讨论二维平面上的 TSP 问题，其距离矩阵满足对称性以及三角不等式：$d (i, j) = d ( j, i),\quad d (i, k ) + d ( k, j) \geqslant d ( i, j )$
• 当退火过程完成以后，最终的路径即为近似最短路径，而评价函数值为对应的路径长度

---

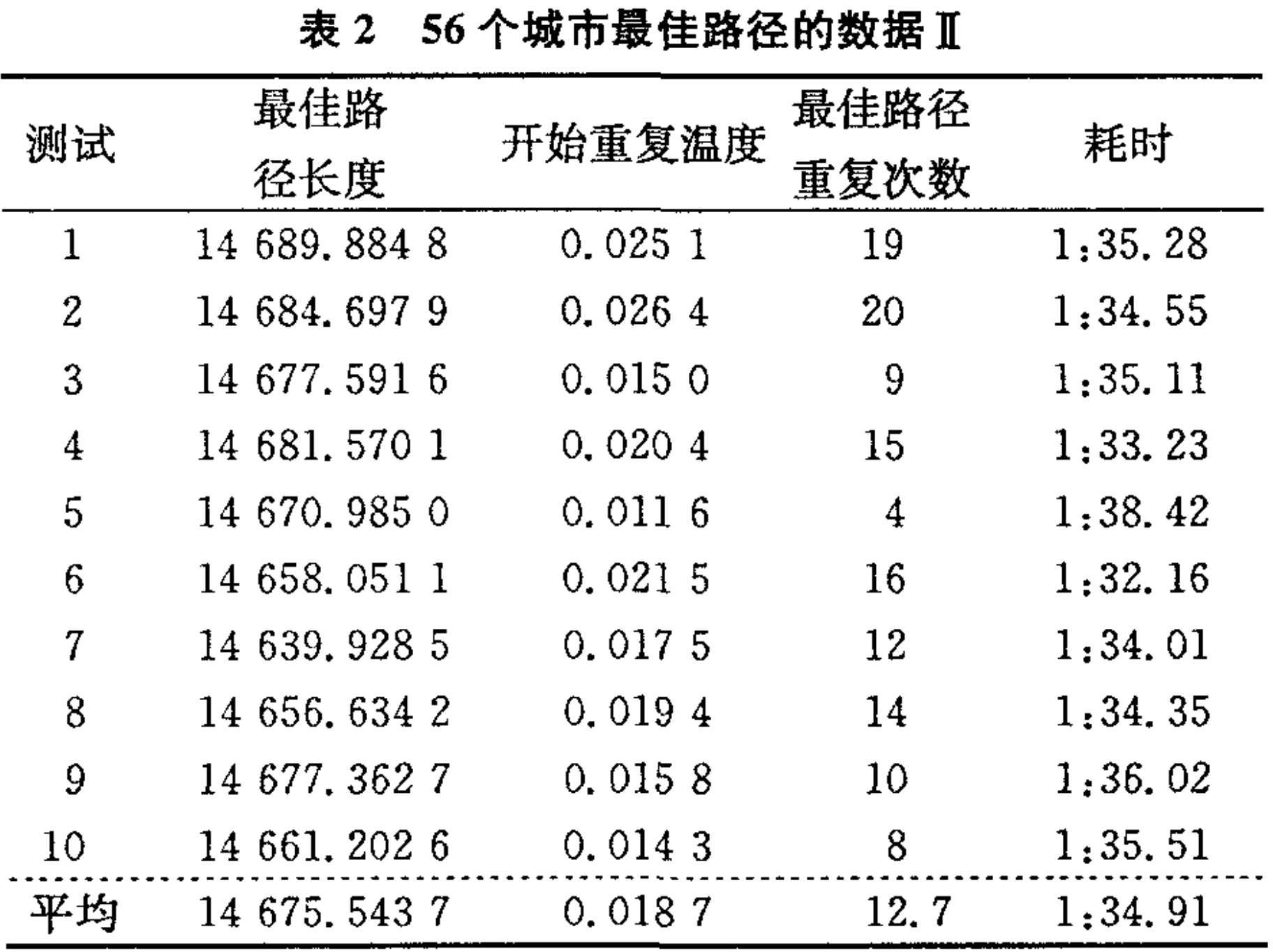
参数设置

• 模拟退火算法中关键参数的研究. 刘洪普, 侯向丹. 计算机工程与科学. Vol. 30, No. 10, 2008, 55-57
• 优化参数
  
  • $\alpha=0.95$
  • 内层循环 $56^3$ 左右
  • 外层循环 399 次
  • 终止温度 0.1

---

14.4 模拟退火算法的优缺点

• 优点：
  
  • 高效：可以在相对较短的时间内得到较好的近似解，允许任何初始解，前期准备工作较少
  • 健壮：算法受初值、解空间规模、问题实例等因素的影响较小，算法依概率收敛到全局最优解
  • 通用、灵活：是一种通用算法，受问题背景影响较小，容易与其他方法结合
• 不足：
  
  • 评价函数，初始温度，退火方式等因素的设置没有确定的方法，需要经验和技巧
  • 实际效果受参数的影响较大

---

课后思考

（$\star\star\star\star$）结合实例（自编或查阅文献）对遗传算法与模拟退火算法进行比较。要求：给出背景问题的描述、说明算法实现的关键点和实验结果的对比.