第二十一讲 点估计的评价准则

概率论与数理统计 讲义 NUDT 2023SP

---

---

21.1 点估计的概念

在已知总体分布类型的情况下，对其中的未知参数 $\theta$ 的 点估计(point estimation) 就是要给出某个与 $\theta$ 对应的统计量（估计量，estimator），进而利用所获得的样本数据，给出一个相对合理的 $\theta$ 的 估计值（estimate）.

• $\theta$ 的点估计量/值一般均记为 $\bbox[yellow]{\hat{\theta}.}$
• 如果只需要给出 $\theta$ 的某个取值范围，则相应的估计称为 区间估计(confident interval).

---

例： 已知关于某项数量指标的 20 个直接观测值

$$\begin{array}{c} 24.46\;25.61\;24.46\;25.61\;26.66\;27.15\;27.31\;27.54\;27.74\;27.94\\ 27.98\;28.04\;28.28\;28.49\;28.50\;28.87\;29.11\;29.13\;29.50\;30.88 \end{array}$$

假设总体服从以 $\mu$ 为均值的正态分布. 如何估计 $\mu$ 的值?

• 因为测量误差的存在，$\mu$ 的精确值是不可能直接得到的.
• 即使用到了再多的数据，都不可能反映总体的全部信息，而只能说是对总体的一个抽样.

---

分析：

1. 使用 $\overline{X}$ 作为估计量, 则估计值为 $\displaystyle \overline{x}=\frac{1}{n}\sum_{i=1}^{20}x_i=27.793$.
2. 使用 $\frac{1}{2}\left(\min\limits_{1\leq i\leq 20}X_i+\max\limits_{1\leq i\leq 20}X_i\right)$ 作为估计量,
   
   • 估计值为 $(24.46+30.88)/2=27.670$.

3. 使用 $\overline{X}_{\mathrm{tr}(10)}$ 作为估计量, 估计值 $\overline{x}_{\mathrm{tr}(10)}=27.838$.

   • $\overline{X}_{\mathrm{tr}(10)}$ 表示去掉最大和最小的各 $10\%$ 的样本后取平均.

   • 可能的估计量很多，如何评价哪一个更好呢？

---

21.2 无偏性

设 $\hat{\theta}$ 是参数 $\theta$ 的点估计，称 $\bbox[yellow]{b(\hat{\theta})=E(\hat{\theta})-\theta}$ 为该点估计的偏差 (bias).

• 若对任意的 $\theta$ 均有 $b(\hat{\theta})=0$，则称 $\hat{\theta}$ 是参数 $\theta$ 的无偏估计量 (unbiased estimator)
• 例： 若 $X_1,X_2,...,X_{n}$ 是来自 $b(1,p)$ 的样本，则 $\hat{p}=\frac{1}{n}\sum\limits_{i=1}^nX_i$ 是参数 $p$ 的无偏估计.

---

例：无偏性的判定

设 $X_1,X_2,...,X_n$ 是来自 $U(0,\theta)$ 的样本, 试判断

$$X_{(n)}=\max\limits_{1\leq i\leq n}X_i$$

是否为 $\theta$ 的无偏估计?

---

分析：

• 利用随机变量最小值的密度函数公式，可得 $X_{(n)}$ 的密度函数
  
  • $\displaystyle f_{n}(x)=\left\{\begin{array}{cc}\displaystyle \frac{nx^{n-1}}{\theta^n} & 0<x<\theta\\ 0 &\text{其他}\end{array}\right.$,
• 于是 $\displaystyle E\left(X_{(n)}\right)=\int_{0}^{\theta}xf_{n}(x)\mathrm{d}x=\frac{n}{n+1}\theta$.
• 由此可知 $X_{(n)}$ 不是 $\theta$ 的无偏估计.

---

渐进无偏估计

• 上例中，因为 $E\left(X_{(n)}\right)=\frac{n}{n+1}\theta\ne\theta$，故 $X_{(n)}$ 不是 $\theta$ 的无偏估计.
• 不难发现，若令 $\displaystyle \hat{\theta}=\frac{n+1}{n}X_{(n)}$, 则 $\hat{\theta}$ 是 $\theta$ 的一个无偏估计.
  
  • 通过对有偏估计的修正，可以得到无偏估计.
• 此外，因为 $\bbox[yellow]{\lim\limits_{n\to\infty}E\left(X_{(n)}\right)=\theta}$, $X_{(n)}$ 可被称为 $\theta$ 一个渐进无偏估计 (asymptotical unbiased estimator).

---

总体均值与方差的无偏估计

定理： 设 $X_1,X_2,...,X_n$ 为来自某总体的样本，该总体具有有限的均值 $\mu$ 和方差 $\sigma^2$. 则

$$\bbox[yellow]{E(\overline{X})=\mu,\quad E(S^2)=\sigma^2.}$$

也即 $\hat{\mu}=\overline{X},\hat{\sigma}^2=S^2$ 分别为 $\mu$ 和 $\sigma^2$ 的无偏估计.

• 推论： $\tilde{S}^2$ 是 $\sigma^2$ 的渐进无偏估计，即 $\lim\limits_{n\to\infty}\tilde{S}^2=\sigma^2$.

---

证明： 对任意 $i=1,2,...,n$，

• $\displaystyle E(X_i\overline{X})=\frac{1}{n}\left[ E(X_i^2)+\sum\limits_{j\ne i}E(X_iX_j) \right]\displaystyle =\frac{1}{n}\left[ \sigma^2+\mu^2+\sum\limits_{j\ne i}E(X_i)E(X_j) \right]=\frac{1}{n}\left( \sigma^2+n\mu^2\right)$
• $\displaystyle E(S^2)=\frac{1}{n-1}\sum\limits_{i=1}^{n} E[(X_i-\overline{X})^2]$
  
  • $\displaystyle =\frac{1}{n-1}\sum\limits_{i=1}^{n}\left[ E(X_i^2)-2E(X_i\overline{X})+E(\overline{X}^2) \right]$
  • $\displaystyle =\frac{1}{n-1}\sum\limits_{i=1}^{n}\left[\sigma^2+\mu^2-\frac{2}{n}(\sigma^2+n\mu^2)+\frac{\sigma^2}{n}+\mu^2\right]=\sigma^2$

---

例：进一步的讨论

设 $X_1,X_2,...,X_n$ 为来自总体 $U(0,\theta)$ 的样本, 可以证明

$$\hat{\theta}_1=\frac{n+1}{n}X_{(n)}, \quad\quad \hat{\theta}_2=2\overline{X}$$

均为 $\theta$ 的无偏估计.

• 问：以上哪一个估计“更好”？

---

分析：

• 相对而言，可能得到的估计值分布越集中，则单次估计的结果就越倾向于接近参数的真值.
  
  • 好的估计量应该具有较小的方差！
• $\displaystyle D\left(\hat{\theta}_1\right)=\frac{\theta^2}{n(n+2)},\quad D\left(\hat{\theta}_2\right)=\frac{\theta^2}{3n}.$
• $n>1$ 时, 总有 $D\left(\hat{\theta}_1\right)<D\left(\hat{\theta}_2\right).$
• 因此，虽然同为无偏估计，但使用 $\hat{\theta}_1$ 作为估计量应该效果会更好.

---

例：德军坦克数量的估计

• “二战”中, 盟军在多次战斗中缴获共计 50 辆德军虎式坦克.
• 假设所有的德军坦克是按顺序编号的.
• 试估计其坦克的数量.

---

仿真对比（真值：1355）

---

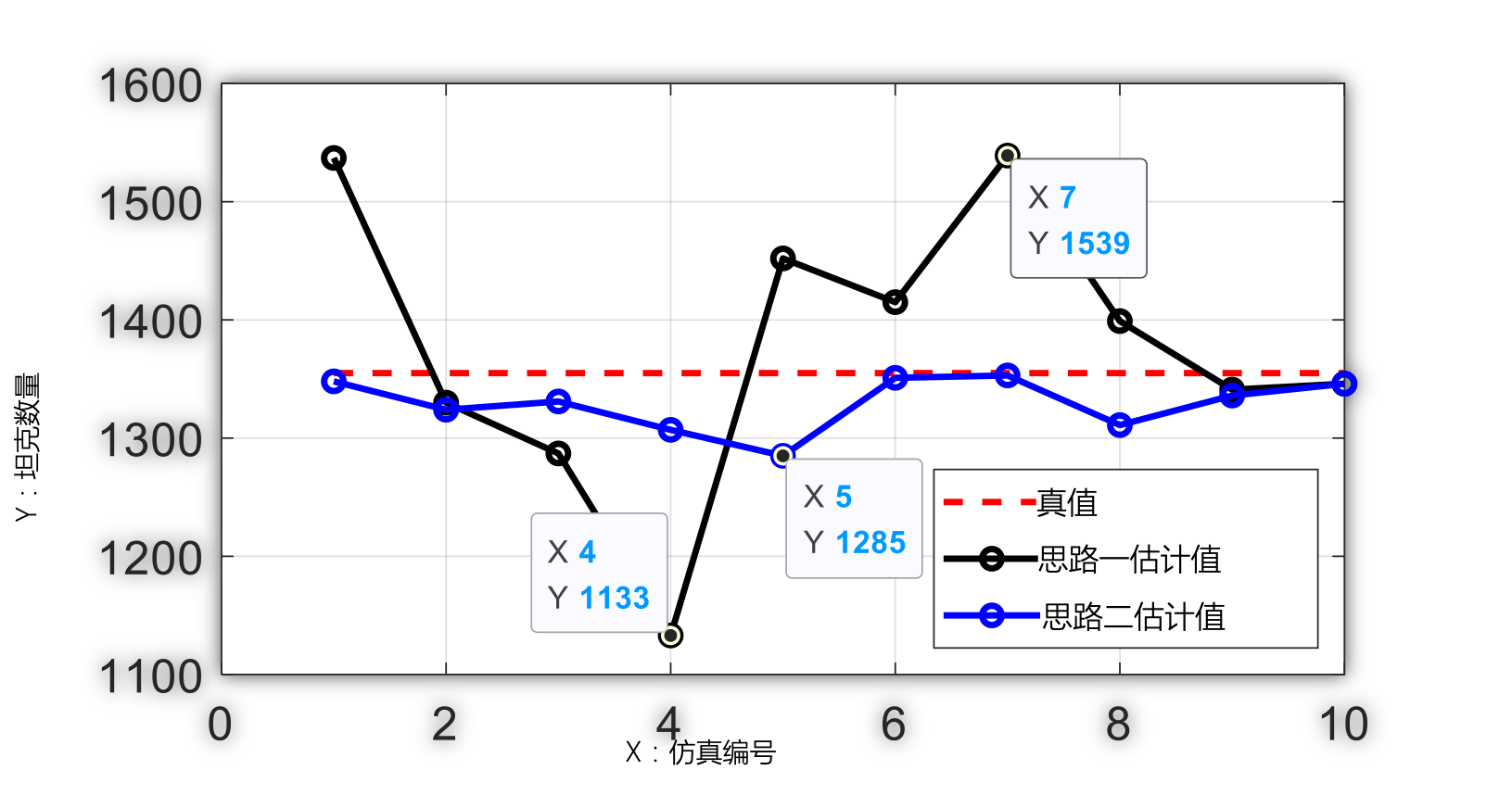
分析：

• 假设坦克从 $1$ 到 $N$ 连续编号，随机被缴获.
• 思路一：$\overline{X}=\frac{1}{50}\sum\limits_{i=1}^nX_i\approx\frac{1+N}{2}.$
  
  • $N$ 的无偏估计 $\overline{N}_1=2\overline{X}-1.$
• 思路二： 缴获的最大编号 $X_{\max}\approx N$
  
  • $N$ 的无偏估计 $\overline{N}_2=X_{\max}.$

---

最小方差无偏估计

在 $\theta$ 的所有无偏估计量中，方差最小的称为 $\theta$ 的 最小方差无偏估计 (minimum variance unbiased estimator，MVUE).

• 定理：设 $X_1,X_2,...,X_n$ 是来自 $N(\mu,\sigma^2)$ 的样本，则 $\overline{X}$ 是 $\mu$ 的 MVUE.

---

21.3 有效性

若估计量 $\hat{{\theta}}=\hat{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 的方差存在，则称

$$\bbox[yellow]{r(\hat{\theta})=E\left[(\hat{\theta}-\theta)^2\right]}$$

为该估计量的 均方误差(mean square error, MSE).

• 若 $\theta$ 的两个估计量 $\hat{\theta}_1,\hat{\theta}_2$ 满足 $r(\hat{\theta}_1)< r(\hat{\theta}_2)$, 则称 $\hat{\theta}_1$ 较 $\hat{\theta}_2$ 更为有效 (more effecient).

---

最小均方误差估计量

若 $\theta$ 的估计量 $\hat{\theta}^*$ 满足：对 $\theta$ 的任意估计量 $\hat{\theta}$，均有

$$r(\hat{\theta}^*)\leq r(\hat{\theta}),$$

则 $\hat{\theta}^*$ 称为 $\theta$ 的最小均方误差估计( minimum mean square error estimator，MMSEE)

• 注：最小均方误差估计不一定是无偏估计！

---

误差(Error)与波动(Fluctuation)

• 绝对误差 (Absolute Error): $\bbox[yellow]{r(\hat{\theta})=E\left[(\hat{\theta}-\theta)^{2}\right]}$
  
  • 估计量与真值的均方误差
• 系统误差 (Systematic Error): $\bbox[yellow]{b(\hat{\theta})=E(\hat{\theta})-\theta}$
  
  • 期望（波动中心）与真值的差
• 随机误差 (Random Error): $\bbox[yellow]{D(\hat{\theta})=E\left[(\hat{\theta}-E(\hat{\theta}))^{2}\right]}$
  
  • 估计量自身的发散程度（波动幅度）

---

绝对误差 = 系统误差 + 随机误差

定理: $\bbox[yellow]{r(\hat{\theta})=D(\hat{\theta})+[b(\hat{\theta})]^{2}.}$

• 推论: 以均方误差作为综合评判标准的前提下，在参数的无偏估计量中，方差越小的越有效.

---

证明：

• $E[\hat{\theta}-E(\hat{\theta})]=E(\hat{\theta})-E(\hat{\theta})=0$.
• $r(\hat{\theta})=E\left[(\hat{\theta}-\theta)^{2}\right]=E\left\{[(\hat{\theta}-E(\hat{\theta}))-(\theta-E(\hat{\theta}))]^{2}\right\}$
  
  • $=E\left[(\hat{\theta}-E(\hat{\theta}))^{2}\right]+E\left[(\theta-E(\hat{\theta}))^{2}\right]-2 E[(\hat{\theta}-E(\widehat{\theta}))(\theta-E(\widehat{\theta}))]$
  • $=D(\widehat{\theta})+(\theta-E(\widehat{\theta}))^{2}=D(\widehat{\theta})+[b(\widehat{\theta})]^{2}$.

---

21.4 相合性 (一致性)

如果参数 $\theta$ 的估计量 $\hat{\theta}_{n}=\hat{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 满足：

$$\bbox[yellow]{\hat{\theta}_n\xrightarrow{\;P\;}\theta,}$$

则称 $\hat{\theta}_{n}$ 是 $\theta$ 的一个 相合估计 (consistent estimator).

• 相合：随着样本容量的增加，估计值几乎一定会等于真值.
• 无偏：只要估计的次数足够多，估计值的均值将收敛到真值.

---

Khinchin 大数定理

设 $X_1,X_2,...,X_n$ 为来自某个总体的样本，该总体的均值 $\mu$ 和方差 $\sigma^2$ 都存在, 则 $\overline{X}$ 和 $S^2$ 分别为 $\mu$ 和 $\sigma^2$ 的相合估计.

---

综合例题

例： 设 $X_1,X_2,...,X_n$ 为来自某个总体的样本，该总体的均值 $\mu$ 和方差 $\sigma^2$ 都存在, 以下 $\mu$ 的估计量中最有效的是（$\qquad$）

(A) $\displaystyle \hat{\mu}_1=\frac14X_1+\frac12X_2+\frac14X_3$
(B) $\displaystyle \hat{\mu}_2=\frac13X_1+X_2-\frac13X_3$
(C) $\displaystyle \hat{\mu}_3=\frac35X_1+\frac45X_2-\frac25X_3$
(D) $\displaystyle \hat{\mu}_4=\frac16X_1+\frac13X_2+\frac12X_3$

---

例： 设 $X_1, X_2, ..., X_n$ 为来自某总体的样本，该总体的密度函数为

$$f(x ; \theta)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\theta} e^{-\frac{x}{\theta}},} & {x>0} \\ {0,} & {x \leq 0}\end{array},\quad(\theta>0)\right.$$

1. 证明 $\overline{X}, n X_{(1)}$ 均为 $\theta$ 的无偏估计.
2. 判断 $\overline{X}, n X_{(1)}$ 中哪一个更有效.

---

提示：

• $E(\overline{X})=E(X)=\theta$, 因此 $\overline{X}$ 是 $\theta$ 的无偏估计.
• 由最小值的密度函数公式，可得 $\displaystyle X_{(1)}\sim\mathrm{Exp}\left(\frac{n}{\theta}\right)$,
  
  • 其密度函数为 $f_{1}(x)=\left\{\begin{array}{cc}\displaystyle \frac{n}{\theta}\mathrm{e}^{-\frac{n}{\theta}x} & x\geq 0\\ 0 & \text{其他}\end{array}\right.$
• 进而 $\displaystyle E(nX_{(1)})=n\cdot\frac{\theta}n=\theta$.
• 由此可知 $nX_{(1)}$ 也是 $\theta$ 的无偏估计.

---

• $D(X)=\theta^2$.
• $\displaystyle D(\overline{X})=D\left(\frac{1}{n} \sum_{i=1}^{n} X_{i}\right)=\frac{D(X)}{n}=\frac{\theta^{2}}{n}$.
• $\displaystyle D(X_{(1)})=\frac{\theta^2}{n^2}$.
• $D(nX_{(1)})=n^2D(X_{(1)})=\theta^2$.
• 综上可知, 作为 $\theta$ 的估计量, $\overline{X}$ 较 $nX_{(1)}$ 更为有效.

---

小结

• 理解点估计评价的三个准则
• 熟练掌握无偏性的判定和有效性的比较