第二十讲 统计量及其分布

概率论与数理统计 讲义 NUDT 2023SP

---

---

数理统计

数理统计学的任务，统而言之，是如何获得样本（观察或试验结果）和利用样本，以对事物的某些未知方面进行分析、推断以至作出一定的决策. [1]

• 试验设计(Experimental Design)、抽样调查(Sampling Survey) 研究如何收集样本
• 统计推断(Statistical Inference) 在已有样本的情况下进行统计分析

---

数理统计部分的主要内容

1. 抽样分布
2. 参数估计
   
   • 矩估计，最大似然估计
   • 区间估计
3. 参数假设检验
   
   • 均值和方差的检验
   • 单正态和双正态总体的检验

---

20.1 数理统计的基本概念

• 总体 (Population)：研究对象的全体
  
  • 数理统计中的总体通常是指：满足某个分布的随机变量的全体
  • 例如[2]：总体 $X\sim N(\mu,\sigma^2)$ 或 总体 $N(\mu,\sigma^2)$ 或 总体 $X$
• 个体 (Individual)： 组成总体的每一个考察对象，例如：某个服从 $N(\mu,\sigma^2)$ 的随机变量 $X_1$
  
  • 随机变量 (Random Variable，简写 r.v.)：被研究对象的数量指标
• 样本 (Sample)：所有被抽取的个体（随机变量）所组成的集合

---

简单随机样本

设随机变量 $X\sim F(x)$，若 $X_1,X_2,\ldots,X_n$ 相互独立，且与 $X$ 同分布[3]，则称

$$X_1,X_2,\ldots,X_n$$

为来自总体 $X$ 的 简单随机样本(Simple Random Sample，简称 随机样本 或 样本)，称 $n$ 为 样本容量 (Sample Size).

---

样本的二重性

• 试验前，样本是独立同分布的随机变量，记为 $\bbox[yellow,3pt]{X_1,X_2,\ldots,X_n.}$
• 试验后，样本是一组确定的数据（样本观测值，Sample Observation），记为 $\bbox[lightgreen,3pt]{x_1,x_2,\ldots,x_n.}$

---

例 为了考察某种器件的寿命，从一批产品中随机抽取 $8$ 件产品进行了寿命试验，得到试验结果如下：

$$8.3,\; 7.7,\; 8.6,\; 8.0,\;8.6,\;7.7,\;8.6,\;8.0.$$

• 样本容量 $n=8$.
• 二重性
  
  • 样本 $X_1,X_2,\ldots,X_8$ 是独立同分布的随机变量.
  • 样本观测值：$8.3, 7.7, 8.6, 8.0,8.6,7.7,8.6,8.0$.
• 统计推断问题的基本要素：总体及其分布、样本容量、样本观测值.

---

20.2 统计量及其分布

设 $X_1, X_2, ..., X_n$ 是来自总体 $F(x)$ 的简单随机样本，若 $g(x_1, x_2, ..., x_n)$ 是 $n$ 元连续函数，且不含任何未知参数，则称随机变量

$$g(X_1,X_2,\ldots,X_n)$$

为 统计量 (Statistics).

• 统计量是且仅是样本的函数.
• 统计量的分布称为 抽样分布 (Sample Distribution).

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $N(\mu,\sigma^2)$ 的简单随机样本，其中 $\mu,\sigma^2$ 均未知，下列随机变量中哪些是统计量？

$$X_i,\qquad\frac1n\sum_{i=1}^nX_i,\qquad\frac1n\sum_{i=1}^n(X_i-\mu)^2,\qquad\frac1n\sum_{i=1}^n\left(\frac{X_i}{\sigma}\right)^2,\qquad\max_{1\leq i\leq n}\left\{X_i\right\}$$

• 统计量的取值不依赖于未知参数，但其分布一般还是和未知参数相关的.

---

常用的统计量

• 样本均值(Sample Mean) $\displaystyle \bbox[yellow]{\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_{i}}$
• 样本方差(Sample Variance) $\displaystyle \bbox[yellow]{S^{2} = \frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}$
• 样本标准差(Sample Standard Deviation) $S=\sqrt{S^{2}}$
• 修正的样本方差 $\displaystyle \bbox[yellow]{\tilde{S}^{2} = \frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}=\frac{1}{n}\sum\limits_{i=1}^nX_i^2-\overline{X}^2$

---

• 第 k 个次序统计量 (k-th Order Statistics) $X_{(k)}$ 表示从小到大的第 $k$ 个值对应的随机变量
  
  • 样本极小值 (Minima of the Sample) $\bbox[yellow]{X_{(1)}=\min\limits_{1\leq i\leq n}X_i.}$
  • 样本极大值 (Maxima of the Sample) $\bbox[yellow]{X_{(n)}=\max\limits_{1\leq i\leq n}X_i.}$
• 样本极差 (Sample Limit Error) $R_n\triangleq X_{(n)}-X_{(1)}$
• 样本中值 (Sample Median) $M_{0.5}=\left\{\begin{array}{ll}\displaystyle X_{\left(\frac{n+1}{2}\right)} & n\text{为奇数}\\ \displaystyle \frac{1}{2}\left(X_{\left(\frac{n}{2}\right)}+X_{\left(\frac{n}{2}+1\right)}\right) & n\text{为偶数}\end{array}\right.$

---

• 样本 k 阶(原点)矩 (k-th Moment of the Sample) $\displaystyle \bbox[yellow]{A_k\triangleq\frac{1}{n}\sum\limits_{i=1}^nX_i^k,\;\;k=1,2,...}$
• 样本 k 阶中心矩 (k-th Central Moment of the Sample) $\displaystyle \bbox[yellow]{B_k\triangleq\frac{1}{n}\sum\limits_{i=1}^n(X_i-\overline{X})^k,\;\;k=1,2,...}$
• 样本偏度(Sample Skewness) $\displaystyle \hat{\beta}_s\triangleq\frac{B_3}{B_2^{3/2}}$
  
  • 反映样本数据相对于对称状态的偏离程度和偏离方向
• 样本峰度(Sample Kurtosis) $\displaystyle \hat{\beta}_k\triangleq\frac{B_4}{B_2^2}-3$
  
  • 反映总体分布密度曲线在其峰值附近的陡峭程度和尾部粗细

---

样本均值

$$\bbox[yellow]{\overline{X} \triangleq \frac{1}{n} \sum_{i=1}^{n} X_{i}.}$$

• 偏差：样本中的数据与样本均值之差，即：$X_i-\overline{X}$.
• 定理：样本的总偏差之和为零，即 $\displaystyle \bbox[yellow]{\sum\limits_{i=1}^n(X_i-\overline{X})=0.}$
• 定理：数据观测值整体与均值的均方误差（偏差平方和）最小.
  
  • 即：$\displaystyle \bbox[yellow]{\sum\limits_{i=1}^n(X_i-\overline{X})^2=\min\limits_{c\in\mathbb{R}}\sum\limits_{i=1}^n(X_i-c)^2.}$

---

20.3 抽样分布

1. 正态分布
2. $\chi^2$-分布
3. t-分布
4. F-分布

---

Chi 方分布

设 $X_1, X_2, ..., X_n$ 是来自总体 $N(0,1)$ 的简单随机样本，称随机变量

$$\bbox[lightgreen]{\chi^{2} \triangleq \sum_{i=1}^{n} X_{i}^{2}.}$$

的分布为 自由度 (Degree of Freedom) 为 $n$ 的 $\chi^2$-分布 (Chi-Square Distribution). 记为 $\bbox[lightgreen]{\chi^2\sim\chi^2(n).}$

---

Chi 方分布的密度函数

$$f(x)=\left\{\begin{array}{ll}{\displaystyle \frac{1}{2^{n / 2} \Gamma(n / 2)} x^{\frac{n}{2}-1} \mathrm{e}^{-\frac{x}{2}},} & {x>0} \\ {0,} & {x \leq 0}\end{array}\right.$$

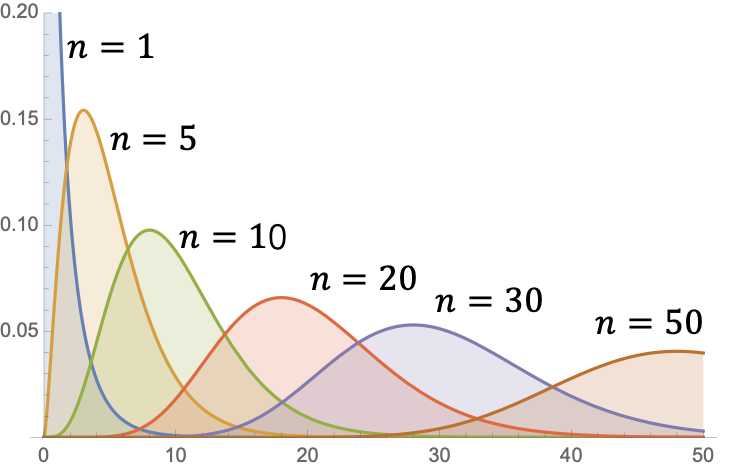
• $\chi^2$ 分布是 Gamma 分布的一个特例.
• $\displaystyle \chi^2(n)=\Gamma\left(\frac{n}{2},2\right)$.

---

Chi 方分布的性质

1. 若 $\chi^{2} \sim \chi^{2}(n)$，则
   
   • $\bbox[lightgreen]{E\left(\chi^{2}\right)=n.}$
   • $\bbox[lightgreen]{D\left(\chi^{2}\right)=2 n.}$
2. 若 $\chi_{1}^{2} \sim \chi^{2}(n), \chi_{2}^{2} \sim \chi^{2}(m)$，且 $\chi_1^2$ 与 $\chi_2^2$ 相互独立，则 $\bbox[lightgreen]{\chi_{1}^{2}+\chi_{2}^{2} \sim \chi^{2}(m+n).}$

---

例 设 $X_i\sim N(0,1)\;(i=1,2,3,4)$ 相互独立，问

$$\frac12 \left(X_1-X_2\right)^2+\frac12 \left(X_3+X_4\right)^2$$

服从什么分布？

• $\displaystyle \frac{X_1-X_2}{\sqrt2}\sim N(0,1)$，$\displaystyle \frac{X_3+X_4}{\sqrt2}\sim N(0,1)$，且相互独立.
• 由 $\chi^2$-分布的定义，
  
  • $\displaystyle \frac12 \left(X_1-X_2\right)^2+\frac12 \left(X_3+X_4\right)^2=\left(\frac{X_1-X_2}{\sqrt2}\right)^2+\left(\frac{X_3+X_4}{\sqrt2}\right)^2\sim\chi^2(2).$

---

t-分布

设 $X\sim N(0,1)$，$Y\sim\chi^2(n)$ 相互独立，则称随机变量

$$\bbox[lightgreen]{t \triangleq \frac{X}{\sqrt{Y / n}}}$$

的分布称为自由度为 $n$ 的 t-分布，记为 $\bbox[lightgreen]{t\sim t(n).}$

• 思考： 设 $X_1,X_2\sim N(0,1)$ 且相互独立，$\displaystyle \frac{X_1}{X_2}\sim t(1)$ 吗？
  
  • 错！应该是 $\displaystyle \frac{X_1}{|X_2|}\sim t(1)$.

---

t-分布的密度函数

$\displaystyle f(x)=\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n \pi} \Gamma(n / 2)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}},$

$$(x\in\mathbb{R})$$

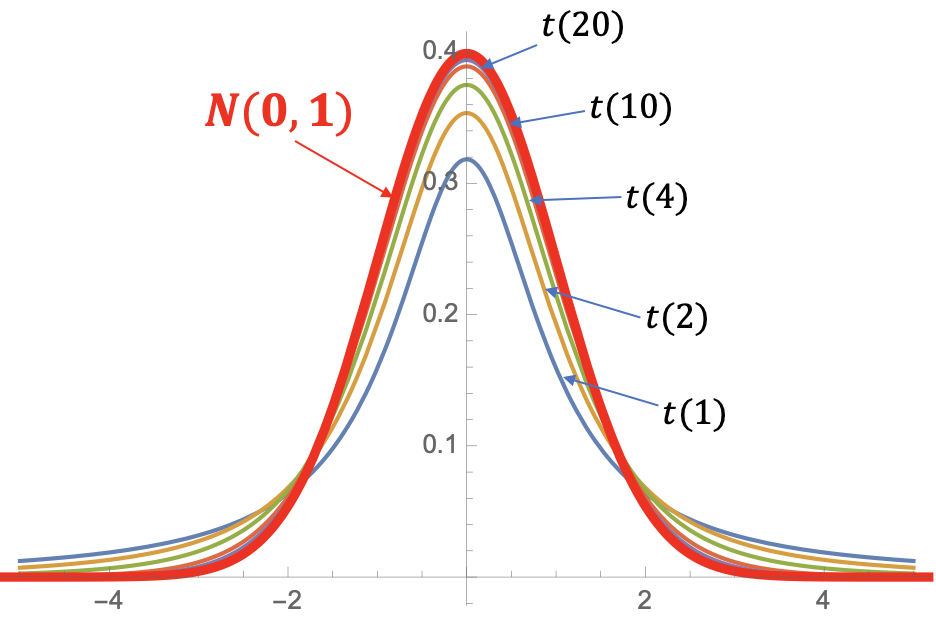
• 随着 $n$ 的增大，$t(n)$ 的概率密度越来越接近于 $N(0,1)$

---

F-分布

设 $X\sim\chi^2(m)$，$Y\sim\chi^2(n)$ 相互独立，则随机变量

$$\bbox[lightgreen]{F \triangleq \frac{X / m}{Y / n}}$$

的分布称为自由度为 $(m,n)$ 的 F-分布.记为 $\bbox[lightgreen]{F\sim F(m,n).}$

• 显然，若 $F\sim F(m,n)$，则 $\frac{1}{F}\sim F(n,m)$.

---

F-分布的密度函数

$$f(x)=\left\{\begin{array}{cc}{\displaystyle \frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma(m / 2) \Gamma(n / 2)} m^{\frac{n}{2}} \frac{n}{(m x+n)^{\frac{m+n}{2}}},} & {x>0} \\ {0,} & {x \leq 0}\end{array}\right.$$

---

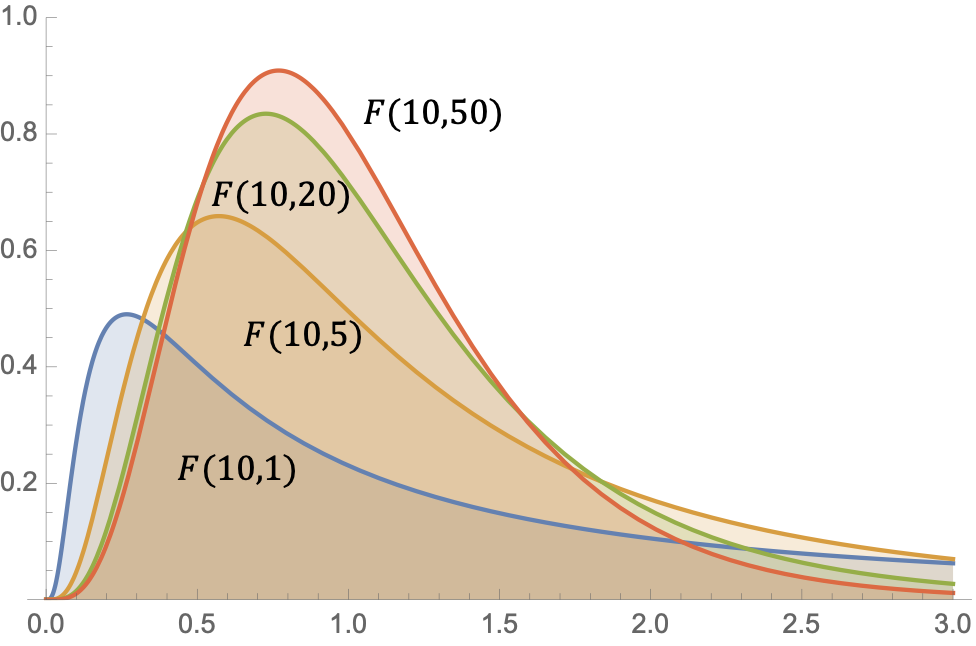
抽样分布的分位点

1. 标准正态分布 $N(0,1)$ 的 $\alpha$ 分位点记为 $\bbox[lightblue,3pt]{u_{\alpha}.}$
   
   • $\bbox[lightblue,3pt]{u_{\alpha}=-u_{1-\alpha}}$
2. $t(n)$ 的 $\alpha$ 分位点记为 $\bbox[lightgreen,3pt]{t_{\alpha}(n).}$
   
   • $\bbox[lightgreen,3pt]{t_{\alpha}(n)=-t_{1-\alpha}(n)}$
3. $\chi^2(n)$ 的 $\alpha$ 分位点记为 $\bbox[yellow]{\chi^2_{\alpha}(n).}$
4. $F(m,n)$ 的 $\alpha$ 分位点记为 $\bbox[pink]{F_{\alpha}(m,n).}$
   
   • $\displaystyle \bbox[pink]{F_{\alpha}(m, n)=\frac{1}{F_{1-\alpha}(n, m)}}$

---

证明：$\bbox[pink]{F_{\alpha}(m, n)=\frac{1}{F_{1-\alpha}(n, m)}}$

• 设 $F\sim F(m,n)$，则 $\frac{1}{F}\sim F(n,m)$.
• $\alpha=P\left\{F\leq F_{\alpha}(m,n)\right\}=P\left\{\frac{1}{F}\geq \frac{1}{F_{\alpha}(m,n)}\right\}.$
• 故 $P\left\{\frac{1}{F}\leq \frac{1}{F_{\alpha}(m,n)}\right\}=1-\alpha$，
• 由此可知 $F_{1-\alpha}(n,m)=\frac{1}{F_{\alpha}(m,n)}.$

---

例 设 $X_1, X_2, ..., X_{10}$ 是来自正态总体 $N(0,4)$ 的简单随机样本，试确定常数 $C$，使得

$$P\left\{\sum_{i=1}^{10} X_{i}^{2}>C\right\}=0.05.$$

---

解：

• $X_{i}\sim N(0,4)$，故 $\displaystyle Y_i=\frac{X_i}2\sim N(0,1)$，$(i=1,2,\ldots,10)$，故 $\displaystyle \sum_{i=1}^{10} X_{i}^{2}=4\sum_{i=1}^{10} Y_{i}^{2}$.
• $\displaystyle 0.05=P\left\{\sum_{i=1}^{10} X_{i}^{2}>C\right\}=P\left\{\sum_{i=1}^{10} Y_{i}^{2}>C/4\right\}=1-P\left\{\sum_{i=1}^{10} Y_{i}^{2}\leq C/4\right\}.$
• 进而 $\displaystyle P\left\{\sum_{i=1}^{10} Y_{i}^{2}\leq C/4\right\}=0.95$.
• 注意到 $\displaystyle \sum_{i=1}^{10} Y_{i}^{2}\sim\chi^2(10)$，故 $C/4=\chi^2_{0.95}(10)$.

---

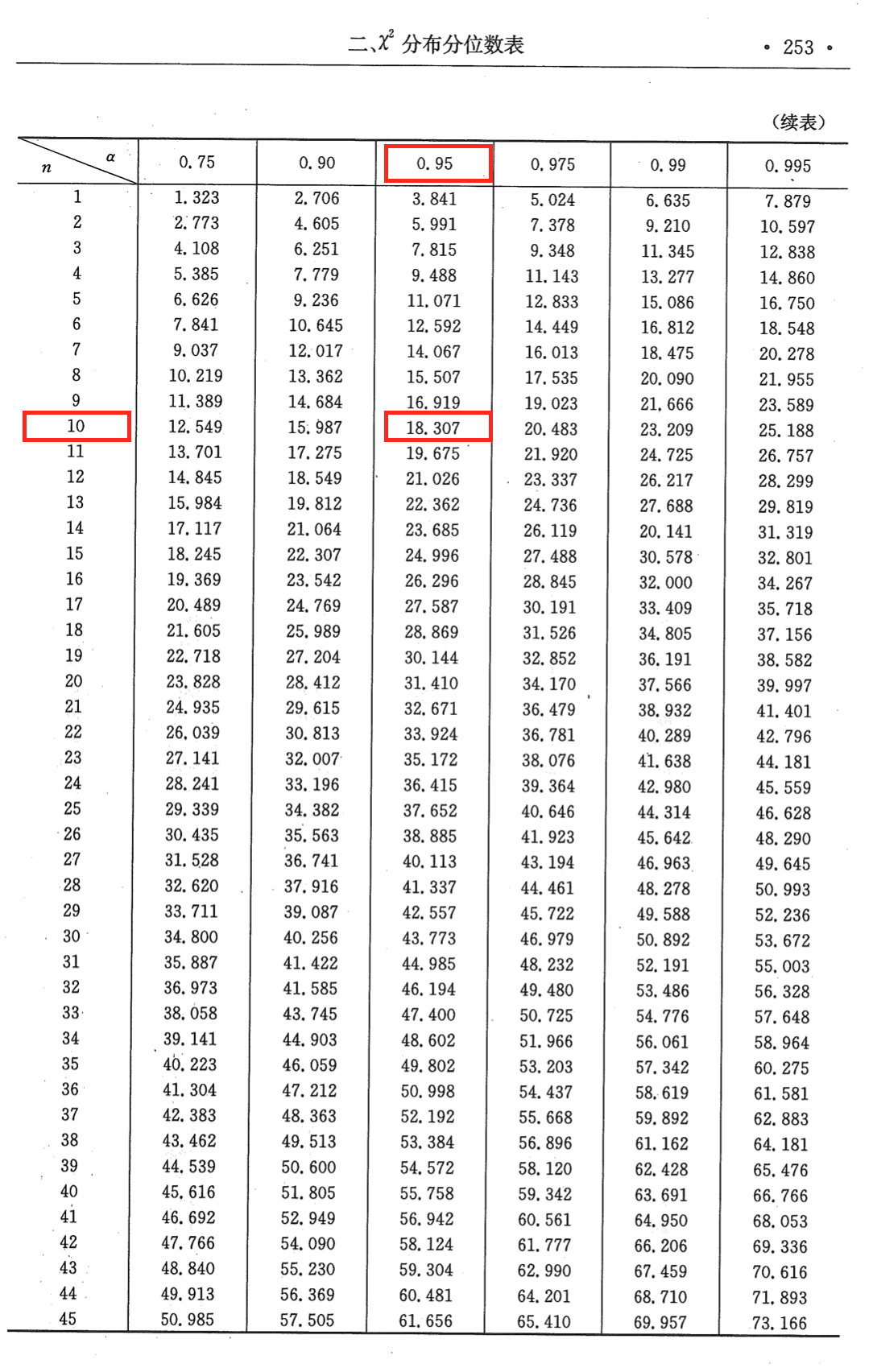
查表求分位点

• 查表可得
  
  • $C/4=\chi^2_{0.95}(10)\approx 18.307$.
• 故 $C\approx 73.228.$

---

20.4 抽样分布定理

---

定理 设 $X_1, X_2, ..., X_n$ 是来自总体 $N(\mu,\sigma^2)$ 的简单随机样本，则

1. $\displaystyle \overline{X} \sim N\left(\mu, \frac{\sigma^{2}}{n}\right).$
   
   • 大量重复试验有助于提高均值的估计精度.
2. $\displaystyle \bbox[yellow]{\frac{(n-1) S^{2}}{\sigma^{2}} \sim \chi^{2}(n-1).}$
3. $\overline{X}$ 与 $S^2$ 相互独立.
   
   • 总体的均值和方差可以分别进行估计.

---

定理 设 $X_1, X_2, ..., X_n$ 是来自 $X\sim N(\mu,\sigma^2)$ 的简单随机样本，则

$$\bbox[yellow]{\frac{\overline{X}-\mu}{{S} / \sqrt{n}} \sim t(n-1).}$$

---

定理 设 $X_1, X_2, ..., X_n$ 和 $Y_1, Y_2, ..., Y_m$ 分别为来自总体 $N(\mu_1,\sigma^2)$ 和 $N(\mu_2,\sigma^2)$ 的简单随机样本，且两者相互独立，则

$$\bbox[yellow]{\frac{(\overline{X}-\overline{Y})-\left(\mu_{1}-\mu_{2}\right)}{S_{\omega} \sqrt{\frac{1}{n}+\frac{1}{m}}} \sim t(m+n-2).}$$

其中 $\displaystyle \bbox[yellow]{S_{\omega}^{2}=\frac{(n-1) S_{1}^{2}+(m-1) S_{2}^{2}}{m+n-2}}$，$S_1^2,S_2^2$ 分别为两个样本对应的样本方差.

---

定理 设 $X_1, X_2, ..., X_n$ 和 $Y_1, Y_2, ..., Y_m$ 分别为来自总体 $N(\mu_1,\sigma_1^2)$ 和 $N(\mu_2,\sigma_2^2)$ 的简单随机样本，且两者相互独立，${S}_{1}^{2},{S}_{2}^{2}$ 分别为其样本方差，则

$$\bbox[yellow]{\frac{{S}_{1}^{2} / \sigma_{1}^{2}}{{S}_{2}^{2} / \sigma_{2}^{2}} \sim F(n-1, m-1).}$$

---

例 设 $X_1, X_2, X_3, X_4$ 是来自总体 $X\sim N(\mu,\sigma^2)$ 的简单随机样本，问 $c$ 取何值时，统计量

$$c \frac{X_{1}-X_{2}}{\left|X_{3}-X_{4}\right|}$$

服从 t-分布，该分布的自由度是多少？

---

分析：

• $X_1-X_2\sim N(0,2\sigma^2),X_3-X_4\sim N(0,2\sigma^2)$.
• 于是 $\displaystyle \frac{X_1-X_2}{\sqrt2\sigma}\sim N(0,1)$，$\displaystyle \frac{X_3-X_4}{\sqrt2\sigma}\sim N(0,1)$.
• 进而 $\displaystyle \frac{|X_3-X_4|^2}{2\sigma^2}\sim\chi^2(1)$.
• 从而 $\displaystyle \frac{\frac{X_1-X_2}{\sqrt2\sigma}}{\sqrt{\frac{|X_3-X_4|^2}{2\sigma^2}}}=\frac{X_1-X_2}{|X_3-X_4|}\sim t(1)$.
• $c=\pm 1$.

---

例 试验 A, B 两种型号的导弹，分别试射了 8 次和 10 次，落点距离靶点的距离分别如下：

A: $14.2,12.6,11.8,12.0,10.4,11.4,12.4,11.8$

B: $11.0,11.4,16.0,15.0,14.0,13.0,11.6,12.2,12.3,12.0$

假定数据均服从正态分布，问：

1. 若判断两种型号的导弹命中精度是否存在差异，应采用何种抽样分布？
2. 若判断两种型号的导弹的精度稳定性是否存在差异，应采用何种抽样分布？

---

例 设 $X_1,X_2,...,X_6$ 是来自总体 $N(0,\sigma^2)$ 的样本，则当 $c=\underline{\hspace{2cm}}$ 时，$\dfrac{c(X_1-X_2)}{\sqrt{(X_3+X_4)^2+(X_5-X_6)^2}}\sim\underline{\hspace{2cm}}$.

---

例 设 $X_1,X_2,...,X_6$ 是来自总体 $N(0,3^2)$ 的简单随机样本，令 $Y=\dfrac{1}{4}\sum\limits_{i=3}^6X_i$，若统计量 $a(X_1+X_2)^2+b\sum\limits_{i=3}^6(X_i-Y)^2$ 服从自由度为 4 的 $\chi^2$-分布，求常数 $a,b$ 的值.

---

小结

• 统计量
  
  • 理解统计量的概念
  • 熟练掌握样本均值和样本方差的各种性质
• 抽样分布
  
  • 熟练掌握四个基本抽样分布的性质和构造特点
  • 熟练掌握和运用四个抽样分布定理

---

• 重点掌握绿色背景的部分

---

The scientist only imposes two things, namely truth and sincerity, imposes them upon himself and upon other scientists.
--Erwin Schrödinger

---

附录：一些相关的计算公式

• 记 $\displaystyle \overline{X}_n=\frac{1}{n}\sum\limits_{i=1}^nX_i$，则
  
  • $\displaystyle \overline{X}_{n+1}=\overline{X}_n+\frac{1}{n+1}(X_{n+1}-\overline{X}_n)$
  • $\displaystyle S_{n+1}^2=\frac{n-1}{n}S_n^2+\frac{1}{n+1}(X_{n+1}-\overline{X}_n)^2$
• 记 $\displaystyle \overline{Y}_n=\frac{1}{n}\sum\limits_{i=1}^nY_i$，则
  
  • $\displaystyle \sum\limits_{i=1}^n(X_i-c)(Y_i-d)=\sum\limits_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})+n(\overline{X}-c)(\overline{Y}-d)$

---

• 抽取两个容量分别为 $n,m$ 的样本，样本均值分别为 $\overline{X^{(1)}},\overline{X^{(2)}}$，修正的样本方差分别为 $S_1^2,S_2^2$
  
  • $\displaystyle S^2=\frac{1}{n^2}\sum\limits_{i<j} (X_i-X_j)^2$
  • $\displaystyle \overline{X}=\frac{n\overline{X^{(1)}}+m\overline{X^{(2)}}}{n+m}$
  • $\displaystyle S^2=\frac{nS_1^2+mS_2^2}{n+m-1}+\frac{nm\left(\overline{X^{(1)}}-\overline{X^{(2)}}\right)^2}{(n+m)(n+m+1)}$
• 设总体的四阶中心矩 $\nu_4=E[X-E(X)]^4$ 存在，$\sigma^2$ 为总体方差，则
  
  • $\displaystyle D(S^2)=\frac{n(\nu_4-\sigma^3)}{(n-1)^2}-\frac{2(\nu_4-2\sigma^4)}{(n-1)^2}+\frac{\nu_4-3\sigma^4}{n(n-1)^2}.$