第六讲 离散型随机变量及其概率分布

概率论与数理统计 讲义 NUDT 2023SP

---

---

回顾：经典的概率模型

• 特点
  
  • 模型简单，易于理解；
  • 样本数不多，便于讨论和研究.
• 不足
  
  • 样本的表达形式多种多样，缺乏统一的数学描述，不便于现代数学工具的应用；
  • 对于如何处理非等可能的概率问题，缺少统一高效的解决思路和处理手段.

---

概率论的现代方法

• 将随机试验的结果完全数字化.
  
  • 引入样本的函数，将样本映射为实数或向量；
  • 开启微积分理论在概率研究中的应用；
  • 给出研究概率问题的更为统一的数学形式.

---

6.1 随机变量的概念

• 随机变量 (Random variable，缩写：rv) 是
  
  • 由样本空间到实数集的映射.
  • $X:\Omega\to\mathbb{R}$ 或 $X(\omega)\in\mathbb{R},\;\omega\in\Omega$
  • 与之相关的概率表示为 $P\{X\in I\}=P\{\omega\in\Omega|X(\omega)\in I\}$，
    
    • 其中 $I\subset\mathbb{R}$ 且 $X^{-1}(I)\in\mathscr{F}$.

---

例： 掷两个骰子(🎲🎲), 观察点数的组合.

• 样本空间: $\Omega=\{(a,b)|a,b=1,2,3,4,5,6\}$
• 问题 I: 求点数之和为 $5$ 的概率.
  
  • 定义 rv: $X(\omega)=a+b$
  • $X\in\{2,3,4,\ldots,12\}$，所求概率为 $P\{X= 5\}$
• 问题 II: 求点数之差的绝对值不超过 $2$ 的概率.
  
  • 定义 rv: $Y(\omega)=|a-b|$
  • $Y\in\{0,1,2,3,4,5\}$，所求概率为 $P\{Y\leq 2\}$

---

例：随机拨打电话号码

进行一项随机试验，随机拨打一个 $8$ 位数的电话号码，尝试该号码是否为有效的.

• 样本：$\omega=8\text{个数字的排列}$.
• 定义随机随机变量 $Y(\omega)=\left\{\begin{array}{ll}1, & \omega\text{是一个有效的电话号码}\\ 0, & \text{其他}\end{array}\right.$.
• 显然，$Y\in\{0,1\}$.
• 使用随机变量使表达形式更为简洁，但也更为抽象.

---

随机变量的分类

• 离散型随机变量 (Discrete Random Variable)
  
  • 值域为可数集 (有限或至多可列个不同取值).
• 连续型随机变量 (Continuous Random Variable)
  
  • 值域可以表示为 $\mathbb{R}$ 上的某个连续区间,
  • 且对任意 $a\in\mathbb{R}$，总有 $P\{X=a\}=0$.
• 不属于以上两类的随机变量，例如：混合型随机变量.

---

6.2 随机变量的概率分布

例： 抛两个骰子(🎲🎲), 观察其点数的组合. 定义 $X$ 为二者点数之和，求概率 $P\{X=3\}$ 和 $P\{X>9\}$.

---

解：假设所有组合出现的概率相同. 样本空间 $\Omega=\{(a,b)|a,b=1,2,\ldots,6\}$, 总点数 $n(\Omega)=36$.

事件 $\{X=3\}=\{a+b=3\}=\{(1,2),(2,1)\}$, 包含 $2$ 个样本，故 $n(\{X=3\})=2$. 从而

$$P\{X=3\}=\frac{2}{36}=\frac{1}{18}.$$

同理，事件 $\{X>9\}=\{(5,5),(5,6),(6,5),(6,6)\}$, $n(\{X>9\})=4$，故

$$P\{X>9\}=\frac{4}{36}=\frac{1}{9}.$$

---

离散型随机变量的分布律

对于离散型随机变量 $X$，定义函数

$$p(x)=P\{X=x\}=P(\{\omega|X(\omega)=x,\omega\in\Omega\})$$

• 称为 $X$ 的分布律, 也称为 概率质量函数 (probability mass function，缩写 pmf)
• 设 $X$ 取值于 $\{x_1,x_2,\ldots\}$，$X$ 的 pmf 常写为
  
  • $p_k=P\{X=x_k\},\;k=1,2,\ldots$

---

例：某品牌电脑的销售中 $80\%$ 为笔记本电脑，剩余的为台式机. 定义随机变量

• $X=\left\{\begin{array}{ll}1& \text{售出的为台式机}\\ 0&\text{售出的为笔记本电脑}\end{array}\right.$
• $X$ 的 pmf $p(x)=\left\{\begin{array}{ll}0.8& x=0\\ 0.2 & x=1 \\ 0 & \text{其他}\end{array}\right.$
• 或 $p_0=P\{X=0\}=0.8,\;p_1=P\{X=1\}=0.2$.

---

pmf 的其他表示方法

表格

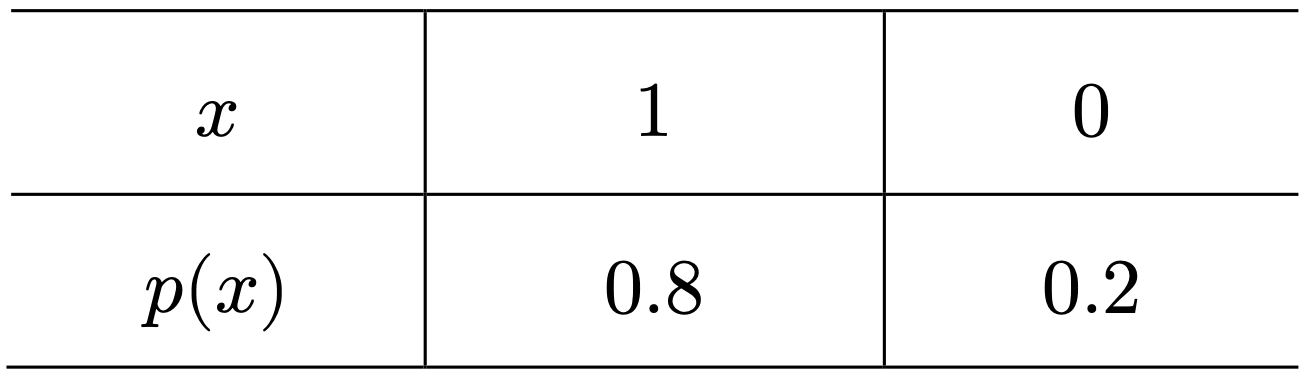
矩阵

$$\begin{pmatrix} 1 & 0 \\ 0.8 & 0.2 \end{pmatrix}$$

图像

---

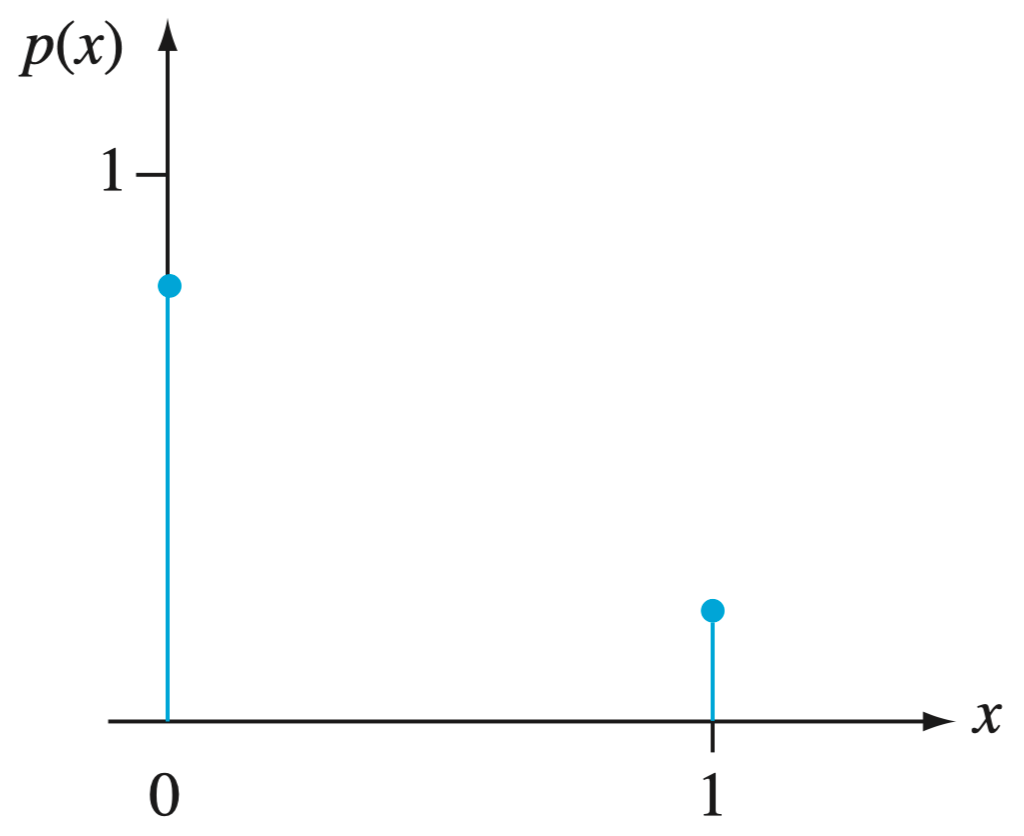
例：抛硬币

抛两个硬币，定义 rv $X$ 等于有字的一面朝上的个数. 求 $X$ 的 pmf.

---

解：$X$ 的取值范围 $\{0,1,2\}$. 样本空间 $\Omega=\{HH,HT,TH,TT\}$，总点数 $n(\Omega)=4$. 不妨假设所有样本点是等可能出现的.

$$\begin{aligned} p(0)&=P\{X=0\}=P(\{TT\})=\frac14\\ p(1)&=P\{X=1\}=P(\{HT,TH\})=\frac24\\ p(2)&=P\{X=2\}=P(\{HH\})=\frac14 \end{aligned}$$

故 $X$ 的 pmf $p(x)=\left\{\begin{array}{ll}0.25& x=0\\ 0.5 & x=1 \\ 0.25 & x=2\\ 0 & \text{其他}\end{array}\right.$

---

pmf 的性质

设 rv $X$ 的 pmf 为 $p(x)$，值域 $\{x_k|k=1,2,\ldots\}$，记 $p_k=p(x_k)$. 则

• 对任意 $k=1,2,3,\ldots$, $p_k\geq0$
• $\sum\limits_kp_k=1$
• 以上两条性质称为 pmf 的本征特性，也即：任意满足以上两条性质的序列 $\{p_k\}$ 都可以视为某个离散型 rv 的 pmf.

---

离散型随机变量的分布函数

设离散型 rv $X$ 的 pmf 为 $p(x)$，$X$ 的概率分布函数 (简称分布函数，缩写 cdf ) 定义为：对任意 $x\in\mathbb{R}$

$$F(x)=P\{X\leq x\}=\sum_{y\leq x}p(y).$$

• 另一种形式：$F(x)=\sum\limits_{x_k\leq x}p_k$

---

cdf 的不同表示形式

函数

$$F(y)=\left\{\begin{array}{ll}0& y<1\\ 0.05 & 1\leq y<2 \\ 0.15 & 2\leq y<4 \\ 0.50 & 4\leq y<8 \\ 0.90 & 8\leq y<16\\ 1 & 16\leq y\end{array}\right.$$

图像

---

cdf 的性质

离散型 rv $X$ 的 cdf $F(x)$ 具有如下的本征特性：

1. $F(x)$ 在 $(-\infty,+\infty)$ 上 单调递增 (不减).
2. $F(x)$ 在任意点处 右连续.
   
   • $F(x)$ 在除 $p(x)>0$ 的点外处处连续.
3. $F(-\infty)=0$, $F(+\infty)=1$

---

6.3 Bernoulli rv

设 rv $X$ 的 pmf 为

$$p(x;\alpha)=\left\{\begin{array}{cl}1-\alpha & x=0\\ \alpha & x=1 \\ 0 & \text{其他}\end{array}\right.$$

则称 $X$ 服从参数为 $\alpha$ 的"0-1"分布 ( Bernoulli 分布，Bernoulli distribution)

• 记为: $X\sim b(1,\alpha)$ 或 $X\sim\mathrm{Bin}(1,\alpha)$

---

Bernoulli 随机变量与 Bernoulli 试验

只有两个不同取值（例如：$0$ 和 $1$）的随机变量称为 Bernoulli 随机变量.

• 结果可以映射为 Bernoulli rv 的试验称为 Bernoulli 试验 (Bernoulli Trial)
  
  • 检查某个产品是否合格.
  • 抛一枚硬币看哪一面朝上.
  • 判断某个新生儿的性别.
  • 某场足球比赛的结果.

---

二项试验

例： 设某条生产线的次品率为 $\alpha\in(0,1)$，且每件产品是否合格相互独立. 随机抽检 $n$ 个产品，定义 rv $X$ 等于其中的次品个数，求 $X$ 的 pmf.

---

解： rv $X$ 的取值范围为 $\{0,1,2,\ldots,n\}$. 样本可表示为一个长度为 $n$ 的序列. 对任意 $k=0,1,\ldots,n$, 事件 $\{X=k\}$，与之对应的样本有 $C_n^k$ 个，每个样本出现的概率为 $\alpha^k(1−\alpha)^{n-k}$. 因此

$$P\{X=k\}=C_n^k\alpha^k(1−\alpha)^{n−k}.$$

rv $X$ 的 pmf

$$p(x)=\left\{\begin{array}{cl}C_n^x\alpha^x(1−\alpha)^{n−x} & x=0,1,\ldots,n\\ 0 & \text{其他}\end{array}\right.$$

---

二项试验与 Bernoulli 试验

由多个独立同分布的 Bernoulli 试验构成的试验，观测其中特定结果的出现次数.

• 检验一批产品，统计其中的次品数量.
• 抛一个硬币多次，记录有字的一面朝上的次数.
• 一批新生儿中男孩的数量.
• 反复尝试同一个挑战性任务，记录成功的次数.
• ...

---

二项随机变量

二项试验对应的随机变量 $X$ 称为二项随机变量 (Binomial rv)，其 pmf 形如：

$$p(x)=\left\{\begin{array}{cl}C_n^x\alpha^x(1−\alpha)^{n−x} & x=0,1,\ldots,n\\ 0 & \text{其他}\end{array}\right.$$

• $X$ 的分布称为 二项分布
  
  • 记为: $X\sim b(n,\alpha)$ 或 $X\sim\mathrm{Bin}(n,\alpha)$
  • “0-1” 分布 $b(1,\alpha)$ 是二项分布的特例

---

综合示例

从 $1,2,3,4,5,6$ 中任选一个数字 $x$，然后从 $1,2,\ldots,x$ 中任选一个数字 $y$，定义 rv $Y=y$. 求 $Y$ 的 pmf 和 cdf.

---

解: 定义 rv $X=x$. 记 $p_Y(y)$ 和 $F_Y(y)$ 分别为 $Y$ 的 pmf 和 cdf.

$$\begin{aligned} p_Y(1)&=P\{Y=1\}\\ &=P\{Y=1|X=1\}P\{X=1\}+P\{Y=1|X=2\}P\{X=2\}\\ &\quad +\ldots+P\{Y=1|X=6\}P\{X=6\}\\ &=1\times\frac16+\frac12\times\frac16+\frac13\times\frac16+\ldots+\frac16\times\frac16=\frac{49}{120} \end{aligned}$$

$$\begin{aligned} p_Y(2)&=P\{Y=2\}\\ &=P\{Y=2|X=2\}P\{X=2\}+P\{Y=2|X=3\}P\{X=3\}\\ &\quad +\ldots+P\{Y=2|X=6\}P\{X=6\}\\ &=\frac12\times\frac16+\frac13\times\frac16+\ldots+\frac16\times\frac16=\frac{29}{120} \end{aligned}$$

---

如此继续，可得 $Y$ 的 pmf

$$p_Y(y)=\left\{\begin{array}{ll}\frac{49}{120}& y=1\\ \frac{29}{120}& y=2\\ \frac{19}{120}& y=3\\ \frac{37}{360}& y=4\\ \frac{11}{180}& y=5\\ \frac{1}{36}& y=6\\ 0&\text{其他}\end{array}\right.$$

---

相应地 $Y$ 的 cdf

$$F_Y(y)=\left\{\begin{array}{cc}0 & y<1\\ \frac{49}{120}& 1\leq y<2\\ \frac{78}{120}& 2\leq y<3\\ \frac{97}{120}& 3\leq y<4\\ \frac{41}{45}& 4\leq y<5\\ \frac{35}{36}& 5\leq y<6\\ 1& 6\leq y\end{array}\right.$$

---

小结

• 求离散型 rv $X$ 的 pmf 的一般步骤
  
  • 给出 $X$ 的取值范围 $\{x_1,x_2,...\}$
  • 对每个 $k=1,2,...$，计算 $P\{X=k\}$
  • 选择合适的形式表达 pmf
    
    • 函数 $p(x)$、分布列 $p_k$、表格、图形
• 利用 pmf 推导 cdf
• 掌握 pmf 和 cdf 的本征特性

---

The essence of mathematics is not to make simple things complicated, but to make complicated things simple.
-- S. Gudder

---

例：女同学的最靠前位次

• 将 $5$ 名男同学和 $5$ 名女同学随机排成一列.
• 定义随机变量 $X$ 为女同学从左到右数的最靠前位次.
• 求 $X$ 的分布律.

---

分析： $X$ 的取值范围为 $\{1,2,3,4,5,6\}$.

$$\begin{array}{ll} P\{X=1\}=\frac{C_5^1\times 9!}{10!}=\frac{1}{2}, & P\{X=2\}=\frac{C_5^1\times C_5^1\times 8!}{10!}=\frac{5}{18},\\ P\{X=3\}=\frac{A_5^2\times C_5^1\times 7!}{10!}=\frac{5}{36}, & P\{X=4\}=\frac{A_5^3\times C_5^1\times 6!}{10!}=\frac{5}{84},\\ P\{X=5\}=\frac{A_5^4\times C_5^1\times 5!}{10!}=\frac{5}{252}, & P\{X=6\}=\frac{5!\times 5!}{10!}=\frac{1}{252}. \end{array}$$

综上，$X$ 的分布律为

$$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ \frac{1}{2} & \frac{5}{18} & \frac{5}{36} & \frac{5}{84} & \frac{5}{252}& \frac{1}{252} \end{pmatrix}.$$

---

例：最大与最小点数

一个均匀的骰子抛掷 $n$ 次. 将所得点数的最小值记为 $X$，最大值记为 $Y$. 求 $X$ 和 $Y$ 的分布律.

---

分析： $X,Y$ 的取值范围分别为 $\{1,2,3,4,5,6\}$.

$$\begin{aligned} P\{X=k\}&=P(\text{所有点数取自}[k,6])-P(\text{所有点数取自}[k+1,6])\\ &=\frac{(6-k+1)^n}{6^n}-\frac{(6-k)^n}{6^n},\quad k=1,2,3,4,5,6.\\ P\{Y=k\}&=P(\text{所有点数取自}[1,k])-P(\text{所有点数取自}[1,k-1])\\ &=\frac{k^n}{6^n}-\frac{(k-1)^n}{6^n},\quad k=1,2,3,4,5,6. \end{aligned}$$

---

例：杯中的最大球数

将 $3$ 个球随机放入 $4$ 个杯子中. 令 $X$ 表示杯子中球的最大数量, 求 $X$ 的分布律.

---

分析： $X$ 的取值范围为 $\{1,2,3\}$.

$$\begin{aligned} P\{X=1\}&=\frac{A_4^3}{4^3}=\frac{3}{8},\quad P\{X=3\}=\frac{C_4^1}{4^3}=\frac{1}{16},\\ P\{X=2\}&=1-P\{X=1\}-P\{X=3\}=\frac{9}{16}. \end{aligned}$$

故 $X$ 的分布律为

$$\begin{pmatrix} 1 & 2 & 3\\ \frac{3}{8} & \frac{9}{16} & \frac{1}{16} \end{pmatrix}.$$