@blueband21c
2023-04-24T12:54:49.000000Z
字数 7044
阅读 7948
第十四讲 联合分布与边缘分布
概率论与数理统计 讲义 NUDT 2023SP
14.1 离散型随机向量
14.1.1 联合分布律
设 均为离散型 rv,则 可称为一个离散型随机向量(Random vector,缩写:rv),其联合分布律 (joint probability mass function,缩写:pmf):
其中 为 的取值范围.
- 本征特性
- 对任意 , .
联合分布律的图像表示
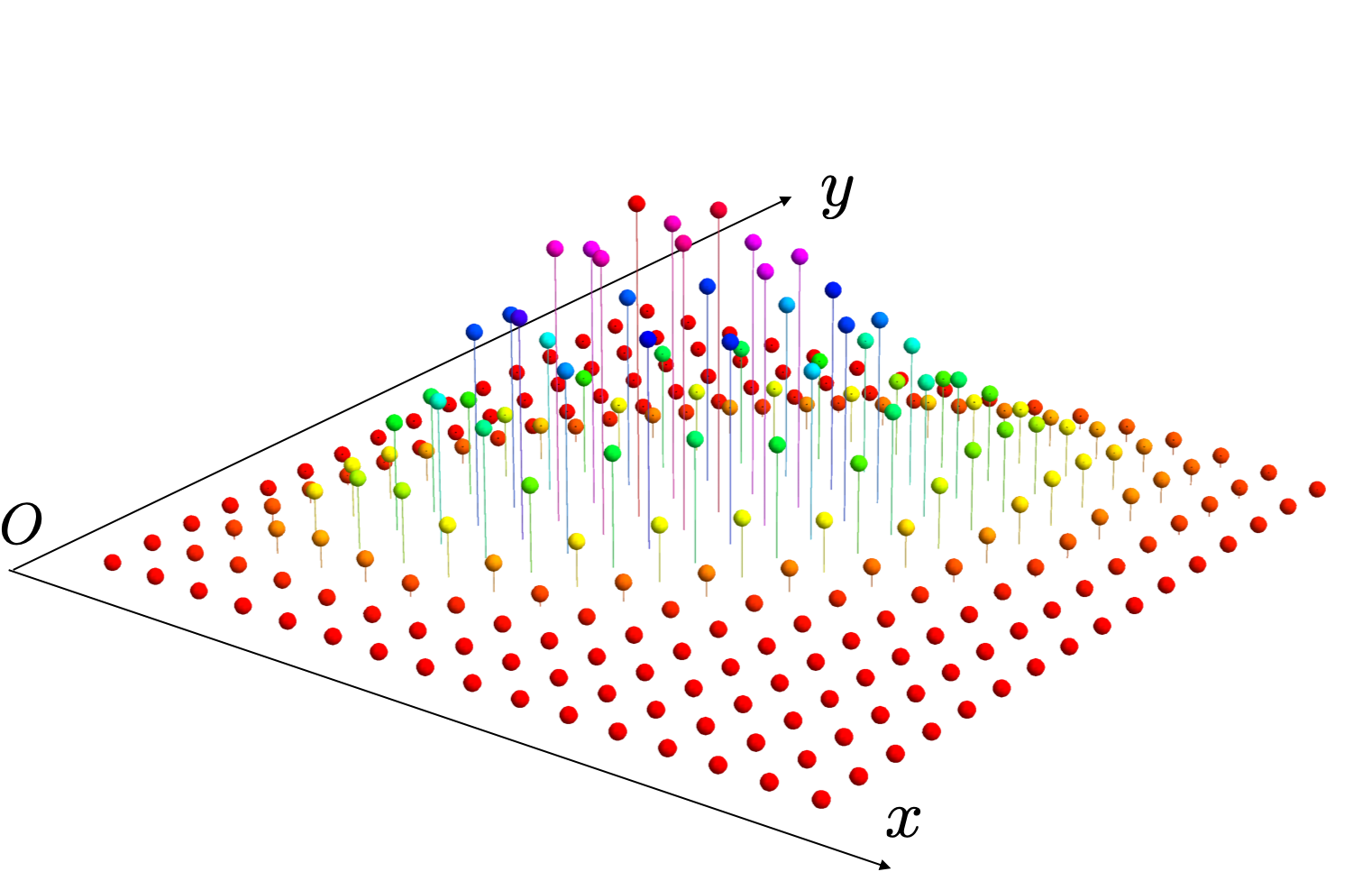
例:前两次命中的联合分布
设某个战士的射击命中率为 . 现让其连续射击,直到命中两次时停止. 记 rv 分别为其第一次和第二次命中时已经射击的次数,求 的联合分布律.
解: 的取值范围 .
当 时, .
若 ,
于是可得 的联合分布律为
例:在一个射击游戏中,参赛选手首先要抛一次骰子,将得到的点数记为 ,然后射击 次,记录命中的次数(记为 ). 已知其单次命中的概率为 . 求 的 pmf.
- 对 ,
-
联合分布律的表格形式
14.1.2 联合分布函数
给定 rv 的 pmf , 其联合分布函数(缩写:cdf)
- 设 的取值范围为 ,且记
- 定义
- 则
联合分布函数的图像
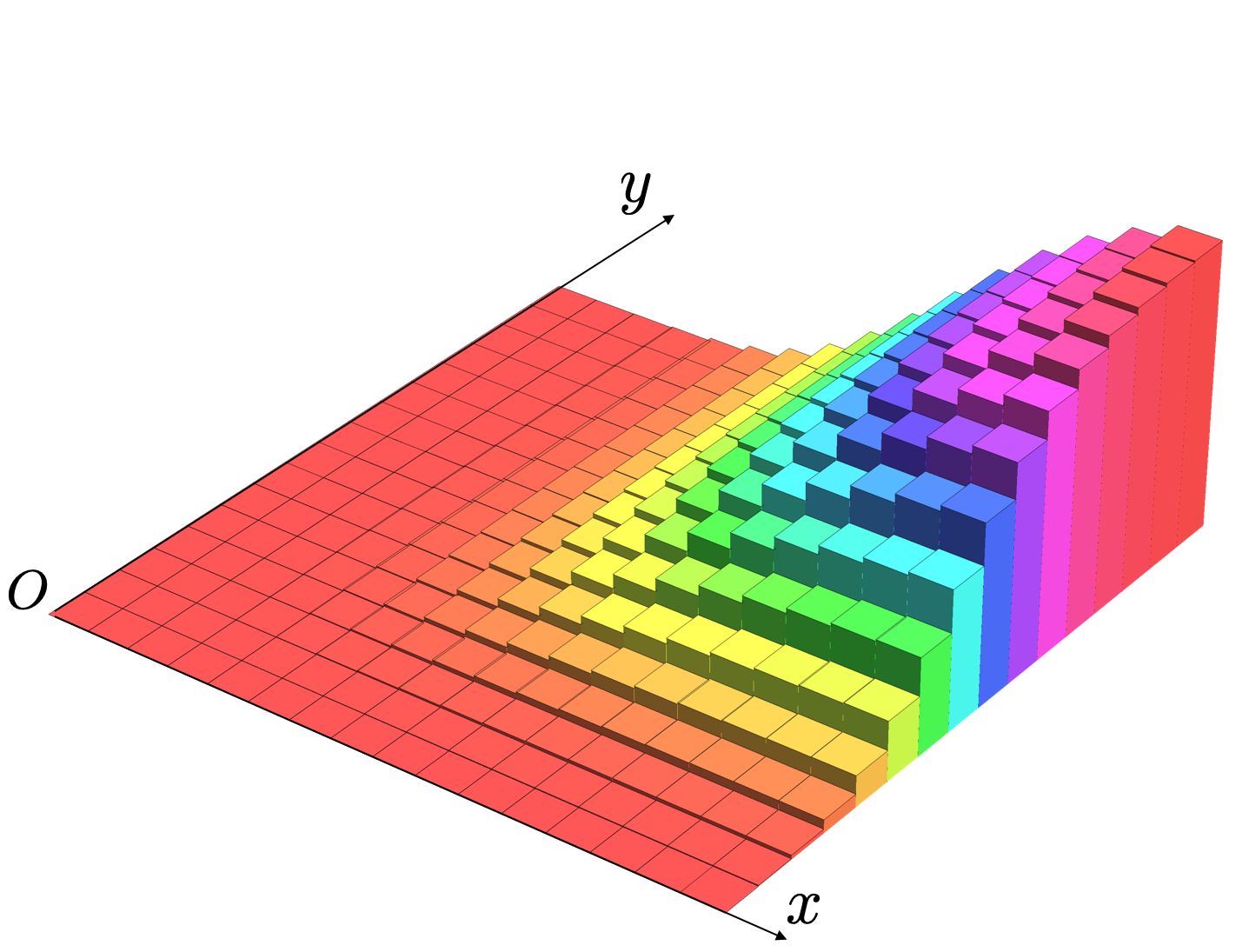
联合分布函数的本征特性[1]
- 分别关于 单调递增
- 对任意
- 关于 均右连续
- 对任意 ,
联合分布函数和一元分布函数的差异
例:验证函数 不可能是一个分布函数.
- 可以验证 满足分布函数的前三条本征特性
- 令 ,
-
14.1.3 边缘分布律
已知 的联合分布律, 的边缘分布律(Marginal pmf,缩写:pmf)
- 边缘分布律就是 自身的分布律!
- 的边缘分布律:
例: 设 rv 是从 中随机抽取的一个数, rv 是从 到 中随机抽取的一个整数. 求 的联合分布律和 的边缘分布律.
- 的取值范围是 .
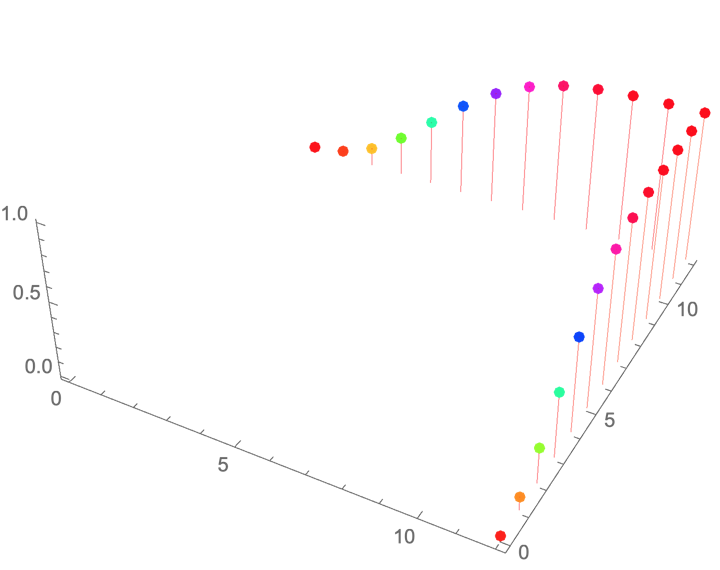
从联合分布律到边缘分布律
13.1.4 边缘分布函数
若 rv 的联合分布函数为 , rv 的(边缘)分布函数分别为 cdf ,则
- 类似地,
14.2 连续型随机向量
14.2.1 联合密度函数
设 均为连续型随机变量,其联合密度函数 ( joint pdf,缩写:pdf ) 满足:对任意
- 的本征特性
- 对任意 ,
联合密度的图像
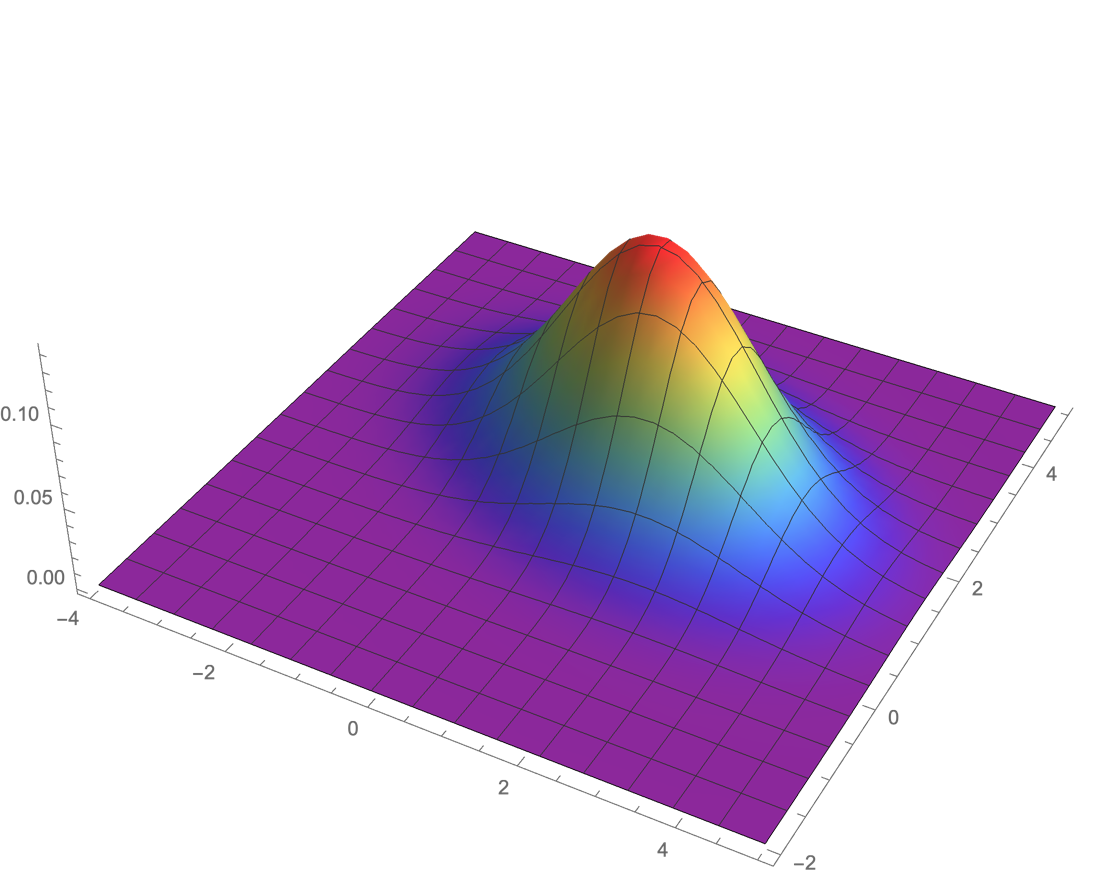
例:利用联合密度计算概率
设 的 pdf 为
求 和 .
解: 由联合密度的本征特性,
故 .
记 , 则
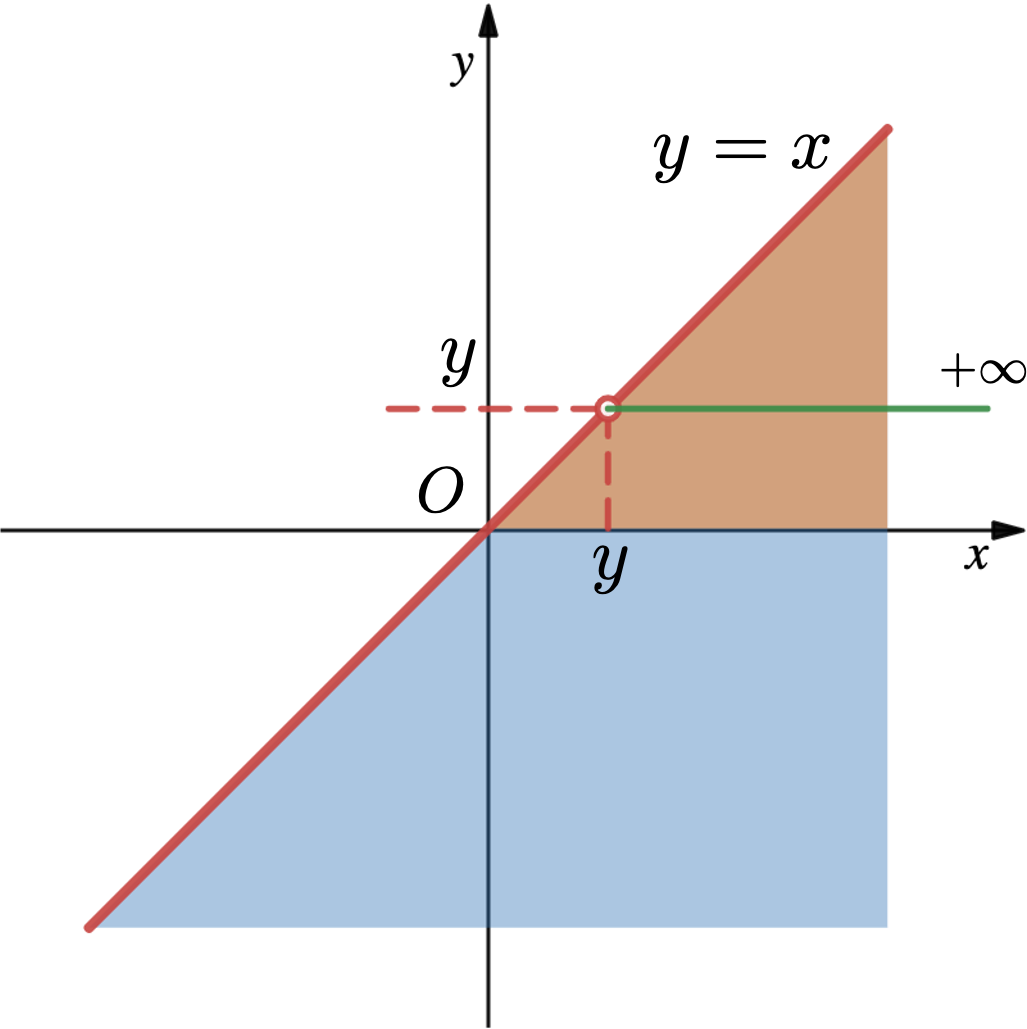
类似地,
14.2.2 联合分布函数
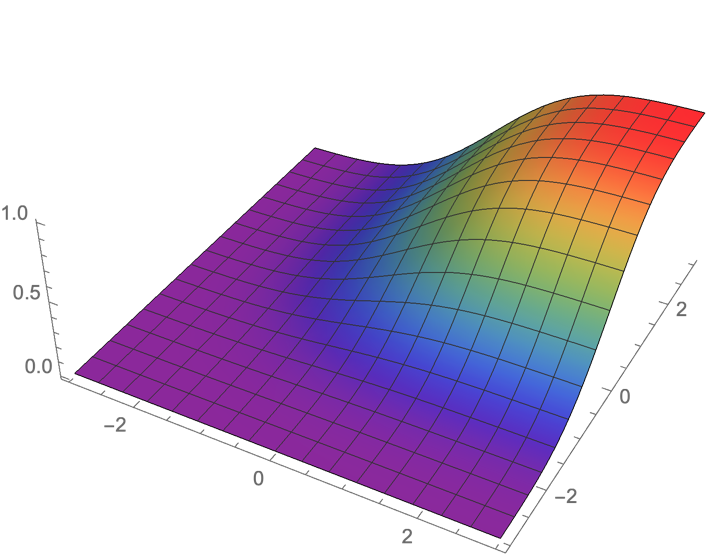
给定 rv 的联合密度,其联合分布函数
联合分布函数的图像
14.2.3 边缘分布函数
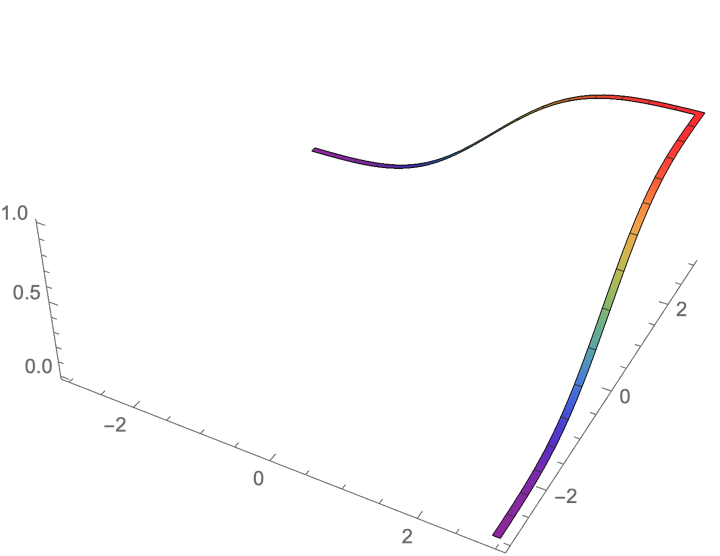
若 rv 的联合分布函数为 , 则 rv 的 (边缘) 分布函数分别为
边缘分布函数的示意图
14.3.4 边缘密度函数
已知 rv 的联合密度 , 的边缘密度函数(marginal pdf,缩写:pdf)分别为
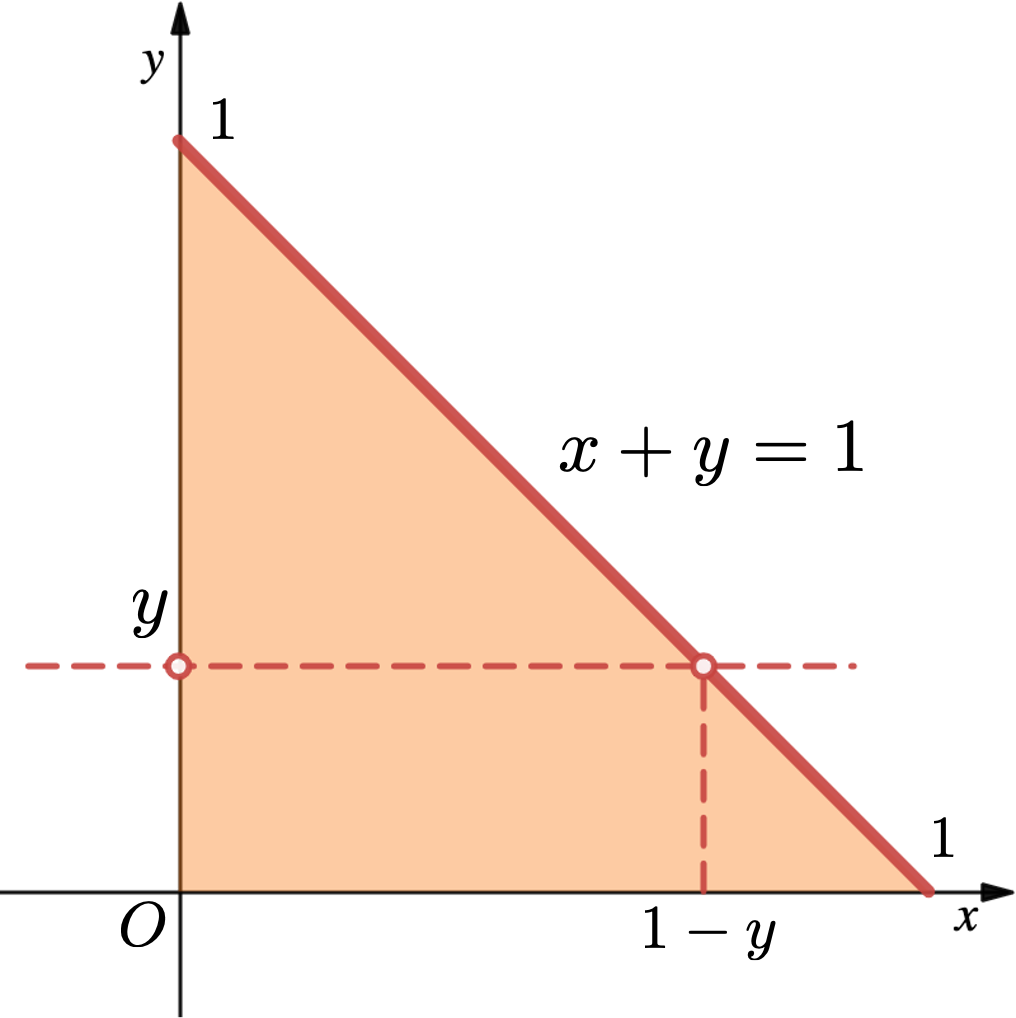
例:已知 rv 的 pdf 为
求 的边缘密度.
解: 由密度函数的本征特性
故 .
小结
- 二维随机向量 的概率分布
- pmf、pdf、cdf
- 联合分布与边缘分布
- 难点:由联合 pdf 求边缘 pdf
联合分布与边缘分布
The definition of a good mathematical problem is the mathematics it generates rather than the problem itself.
-- Sir Andrew John Wiles
