第二十四讲 假设检验的基本概念

概率论与数理统计 讲义 NUDT 2023SP

---

---

24.1 什么是假设检验？

• 提出某种假设，然后利用统计数据判断其真伪.
• 需要回答的问题：
  
  1. 如何（定量地）表达假设？
  2. 真伪的标准是什么？
  3. 用什么样的方法进行判定？
  4. 如何表达/理解检验的结果？

---

两类假设检验问题

1. 参数假设检验
   
   • 总体分布形式 $F(x; \theta)$ 已知，对总体分布中的参数 $\theta$ 进行检验
   • 例如：次品率(均值检验)、质量的对比(方差检验)
2. 非参数假设检验
   
   • 总体的分布未知，对总体的分布或总体间的关系进行检验
   • 例如：判断总体的分布(拟合优度检验)、判断两随机变量是否独立(独立性检验)

---

24.2 参数假设检验

例（产品质量检验） 某车间用一台自动包装机装化肥，每袋的标称重量规定为 $50$ kg. 某日开工后随机抽检 $9$ 袋产品，测得净重如下(单位:kg)

$$49.6, 48.4, 50, 48.6, 50.6, 49.8, 50.2, 49.2, 49.$$

设化肥的实际重量服从正态分布，标准差为 $0.75$ kg，试判断该包装机是否工作正常？

• 数据的平均值：$\overline{x}=49.489$.
• 从以上的数据来看，均值(平均重量)没有达标.
• 考虑到设备和测量可能存在的误差，这样的结果是否一定是不可接受的？

---

问题的背景

• 理论上讲，只有完整地了解了整个总体之后，才能做出正确无误的判断.
• 但这在实际中常常是不可能的.
  
  • 很多情况下，只能根据样本进行 推断.
  • 由于样本未必能够严格反映总体的完整特征，最终推理得到的结论也可能是错误的！
  • 因此，统计推断的结果，只能说是在一定的概率下是正确的.

---

提出假设检验问题

• 已知条件：每袋化肥重量的分布 $N(\mu,(0.75)^2)$，理论上，包装机工作正常，当且仅当 $\mu=50$.
• 待检验的假设
  
  • 原假设（零假设，Null Hypothesis）：$H_0$：$\mu=50$，即：包装机工作正常
  • 备择假设（Alternative Hypothesis）：$H_1$：$\mu\ne 50$，即：包装机工作不正常
• 可能的结论
  
  • 拒绝 $H_0$，认为包装机工作不正常.
  • 接受 $H_0$，认为包装机工作正常.

---

假设检验的思想出发点

• 小概率事件在一次试验中是不会发生的.
  
  • 如果发生了小概率的事件，则意味着原来的判断（原假设）可能是错误的.
• 在假设检验中，如果事实（样本）支持原来判断的反面（备择假设），则拒绝原假设.
  
  • 统计推断的目的是证伪，也就是要尝试验证备择假设是否成立.
  • 如果不能证伪，则接受原假设.

---

错误与风险

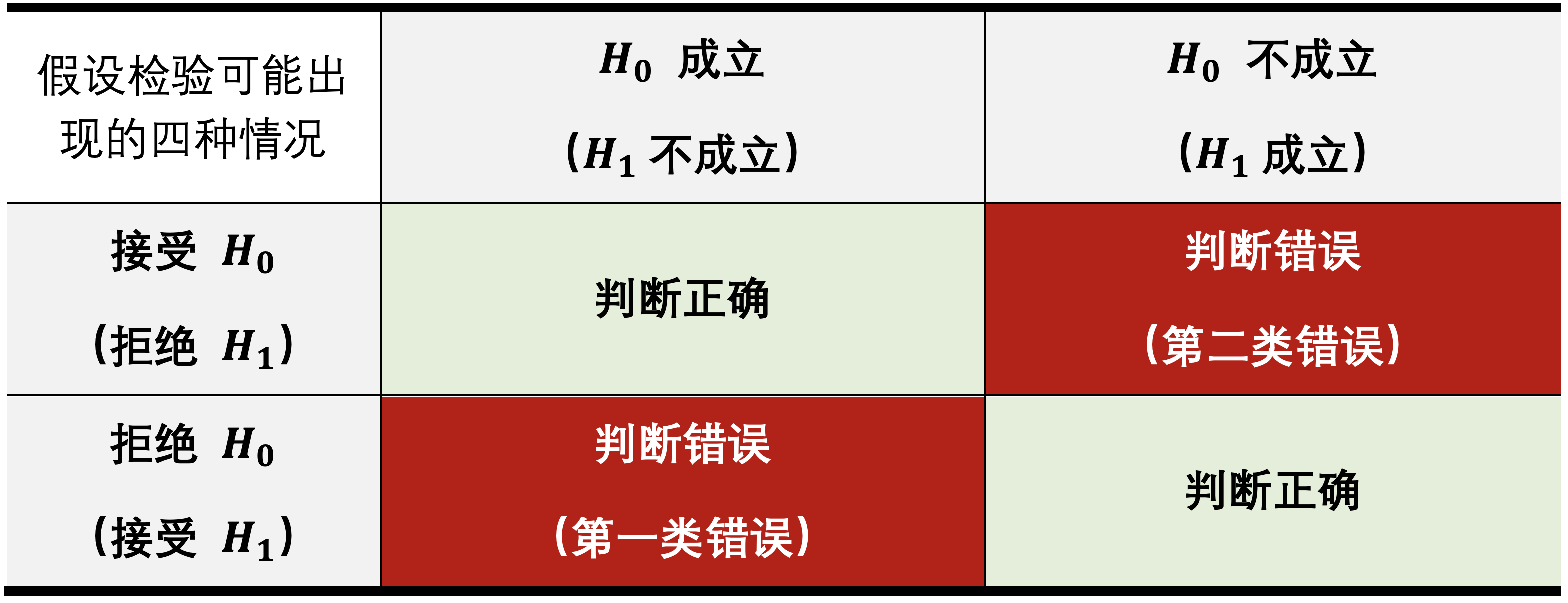
• I 类错误 (False Negative) $H_0$ 为真，却拒绝 $H_0$，

• I 类风险： $P\{\text{拒绝}H_0| H_0\text{为真}\}$

• II 类错误 (False Positive) $H_0$ 为假，却接受 $H_0$

• II 类风险： $P\{\text{接受}H_0| H_1\text{为真}\}$

---

产品质量检验问题的分析

• 待检验的假设：$H_0:\;\mu=\mu_0=50;\quad H_1:\; \mu\ne\mu_0=50$.
  
  • 任务：判断所获得的样本是否支持了 $H_1$，从而决定是否接受 $H_0$.
• 因为 $\overline{X}$ 是 $\mu$ 的无偏估计是 ，因此 $\mu\approx\overline{x}$.
  
  • 若 $H_0$ 成立，$\left|\overline{x}-\mu_{0}\right|$ 应该较小.
  • 反之，若 $\left|\overline{x}-\mu_{0}\right|$ 较大，则有理由认为 $H_0$ 不成立.
• 检验的规则：确定某个阈值 $C$
  
  • 当 $\left|\overline{x}-\mu_{0}\right|>C$ 时，拒绝 $H_0$，否则接受 $H_0$.
  • 满足 $\left|\overline{x}-\mu_{0}\right|>C$ 的样本取值范围称为检验的拒绝域，一般记为 $W_1$.
• 问题：如何确定 $C$？

---

假设检验原则

• 检验原则一：犯 I 类错误的概率要足够小.
  
  • 对给定的 $\alpha\in(0,1)$ (显著性水平, Level of Significance), 满足: $\bbox[yellow]{P\{\text{拒绝}H_0| H_0\text{为真}\}\leq\alpha.}$
  • 除非有足够的证据能够支持备择假设，否则不轻易拒绝原假设.
• 检验原则二：在满足检验原则一的条件下，使 II 类风险尽可能小.
• 通常先利用检验原则一构造检验的拒绝域，再利用检验原则二对其进行优化.

---

产品质量检验的拒绝域

• 根据假设检验原则一
  
  • $\bbox[yellow]{P\{\text{拒绝}H_0| H_0\text{为真}\}\leq\alpha}=P\left\{\left|\overline{X}-\mu_{0}\right| \geq C \bigg| \mu=\mu_{0}\right\}=P\left\{\left|\displaystyle \frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geq \frac{C}{\sigma / \sqrt{n}} \bigg| \mu=\mu_{0}\right\} \leq \alpha$
• $H_0$ 成立时，$X\sim N(\mu_0,\sigma^2)$，故 $\displaystyle \frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}}\sim N(0,1)$
• 任取 $C\geq\displaystyle \frac{\sigma}{\sqrt n}u_{1-\alpha/2}$，即可满足假设检验原则一.
• 例如，可以取一个拒绝域为 $W_1=\left\{(x_1,...,x_n)\bigg||\overline{x}-\mu_0|\geq \frac{\sigma}{\sqrt n}u_{1-\alpha/2}\right\}$.
• 显然，若只考虑检验原则一，拒绝域的取法并不唯一
  
  • 选取的 $C$ 越大， I 类风险越小

---

产品质量检验的解答

解： 检验假设

$$H_0:\;\mu=\mu_0=50;\quad H_1:\; \mu\ne\mu_0=50.$$

拒绝域为

$$W_1=\left\{(x_1,...,x_n)\bigg||\overline{x}-\mu_0|\geq C=\frac{\sigma}{\sqrt n}u_{1-\alpha/2}\right\}.$$

取 $\alpha=0.05$，计算得到: $\overline{x}=49.489$, $C=0.49$.

因为 $|\overline{x}-\mu_0|=0.511>0.49$，故应拒绝 $H_0$，也即认为今天的设备运转不正常.

---

设备真的不正常吗？

• 准确的说法：认为设备运行不正常而实际设备运行正常的可能性不超过 5%.
• 不拒绝原假设可能有两种含义:
  
  1. 原假设的确是正确的，应当接受.
  2. 样本提供的信息不足以拒绝原假设（支持备择假设），只好接受原假设.
• 从这个意义上说，假设检验的原则一可以理解为：保护（不随意否定）原假设.

---

无罪推定原则

• 《刑事诉讼法》第十二条：“未经人民法院依法判决，对任何人都不得确定有罪.”
• 控方需要列举证据证明嫌疑人有罪.
• 如果证据确凿，则推翻无罪假设，嫌疑人被判有罪.
• 如果证据不足，则维持无罪判定，宣布嫌疑人无罪.
  
  • 关在监狱中的人基本上都是有罪的.
  • 监狱外面的人并不全是好人.

---

假设检验的一般步骤

1. 提出待检验的假设：原假设 vs 备择假设.
2. 给出拒绝域的形式.
3. 选择检验统计量，根据显著性水平确定拒绝域.
4. 根据样本数据进行计算，作出判断.

---

1. 提出待检验的假设

$$\bbox[yellow]{H_0:\theta\in\Theta_0,\quad H_1:\theta\in\Theta_1.}$$

• 其中 $\Theta_0\cap\Theta_1=\varnothing$，但不要求一定有 $\Theta_0\cup\Theta_1=\Theta$.
• 如果 $\Theta_0$(或 $\Theta_1$) 只含有一个点，则该假设称为 简单假设，否则称为 复合假设.
• 注意：
  
  1. 原假设中应该包含等号.
  2. 通常情况下，应该将不应该/不希望轻易加以否定的假设作为原假设.

---

单边假设与双边假设

• 设原假设为 $H_0:\theta=\theta_0$，可能的备择假设通常有三种
  
  1. $H_1':\theta\ne\theta_0.$
  2. $H_1'':\theta<\theta_0.$
  3. $H_1''':\theta>\theta_0.$
• $H_0$ vs $H_1'$ 称为 双侧(边)假设.
• $H_0$ vs $H_1''$ 或 $H_0$ vs $H_1'''$ 称为 单侧(边)假设.

---

2. 给出拒绝域的形式

• 假设检验等价于把样本空间划分为两个不相交的部分 $W_1$ 和 $\overline{W}_1$，其中 $W_1$ 称为 拒绝域 (Rejection Region).
  
  • 当样本 $(x_1,...,x_n)\in W_1$ 时，则拒绝 $H_0$，否则接受 $H_0$.
  • 拒绝域确定了，检验的判断准则也就确定了.
• 假设检验就是要证伪（尝试证明备择假设），因此拒绝域的形式完全由备择假设决定.

---

3. 选择检验统计量，根据显著性水平确定拒绝域

• 根据对 I 类风险的要求，由检验统计量的分布确定分位点.
• 检验统计量不具有唯一性，拒绝域也不具有唯一性.

4. 根据数据进行计算，作出判断.

• 不同的显著性水平可能意味着不同的检验结论.
• 交换原假设和备择假设可能导致判断的结论相反.

---

例：交换原假设和备择假设（1）

某工厂规定特定产品的质量不能低于 $50$ kg，否则视为不合格. 已知该产品的质量服从 $N(\mu,0.25)$. 现抽检 100 件样品，测得样本均值 $\overline{x}=50.05$，试判断该批产品是否达到质量标准. $(\alpha=0.05)$

• $\bbox[lightgreen]{H_0:\mu\geq 50,\quad H_1:\mu<50}$
• 拒绝域 $W_1=\left\{(x_1,x_2,...,x_n)\big|\overline{x}<\mu_0+u_{\alpha}\displaystyle \frac{\sigma}{\sqrt{n}}=49.91\right\}$.
• 结论：接受 $H_0$，认为该批产品合格.

---

例：交换原假设和备择假设（2）

某工厂规定特定产品的质量不能低于 $50$ kg，否则视为不合格. 已知该产品的质量服从 $N(\mu,0.25)$. 现抽检 100 件样品，测得样本均值 $\overline{x}=50.05$，试判断该批产品是否达到质量标准. $(\alpha=0.05)$

• $\bbox[lightblue]{H_0:\mu\leq 50,\quad H_1:\mu>50}$
• 拒绝域 $W'_1=\left\{(x_1,x_2,...,x_n)\big|\overline{x}>\mu_0+u_{1-\alpha}\displaystyle \frac{\sigma}{\sqrt{n}}=50.08\right\}$
• 结论：接受 $H_0$，认为该批产品不合格.

---

检验的 p 值

例 某厂生产的合金强度服从正态分布 $N(\mu,16)$，其中的设计值为不低于 $110$ (Pa). 为保证质量，该厂每天都要对生产情况做例行检查，以判断生产是否正常进行. 某天从生产的产品中随机抽取 $25$ 块合金，测得其强度值均值为 $\overline{x}=108.2$ (Pa)，问当日生产是否正常？

• $H_0:\mu\geq 110,\quad H_1:\mu<110$
• $W_1=\left\{(x_1,x_2,...,x_n)\big|u=\displaystyle \frac{\overline{x}-110}{\sqrt{16}/\sqrt{5}} < u_{\alpha}\right\}$
• 观测结果 $u=-2.25$.

---

不同显著性水平之下的检验结论

$$\begin{array}{c|c|c} \hline \quad \quad \text{显著性水平} \quad \quad & \quad \quad \text{拒绝域} \quad \quad & \quad \quad \text{对应的结论}(u=-2.25)\quad \quad \\ \hline \alpha=0.1 & u< -1.282 & \text{拒绝}H_0\\ \alpha=0.05 & u< -1.645 & \text{拒绝}H_0\\ \alpha=0.025 & u< -1.96 & \text{拒绝}H_0\\ \hline \alpha=0.01 & u> -2.326 & \text{接受}H_0\\ \alpha=0.005 & u>q -2.576 & \text{接受}H_0\\ \hline \end{array}$$

• 检验的 p 值 是指在一个假设检验问题中，利用样本观测值能够做出拒绝原假设的最小的显著性水平. 以上例子中，$p=P\{u\leq -2.25\}=\Phi(-2.25)=0.0122$.

---

置信区间与假设检验的关系

• 设 $X_1,...,X_n$ 是来自总体 $X$ 的样本，$\Theta$ 是总体参数 $\theta$ 的取值范围.
• 设 $\bbox[lightgreen]{(\underline{\theta}(X_1,...,X_n),\overline{\theta}(X_1,...,X_n))}$ 是参数 $\theta$ 的一个置信水平为 $1-\alpha$ 的置信区间. 也即：对任意 $\theta\in\Theta$，有 $P_{\theta}\left\{ \underline{\theta}(X_1,...,X_n)<\theta<\overline{\theta}(X_1,...,X_n) \right\}\geq 1-\alpha$
• 考虑显著性为 $\alpha$ 的双边检验：$\bbox[yellow]{H_0:\theta=\theta_0,\;H_1:\theta\ne\theta_0.}$
• 注意到 $P_{\theta_0}\left\{ \underline{\theta}(X_1,...,X_n)<\theta_0<\overline{\theta}(X_1,...,X_n) \right\}\geq 1-\alpha.$
• 故拒绝域可以取为 $W_1:\theta_0\notin\bbox[lightgreen]{(\underline{\theta}(x_1,...,x_n),\overline{\theta}(x_1,...,x_n))}.$

---

利用置信区间进行假设检验

对于显著性为 $\alpha$ 的双边检验：

$$H_0:\theta=\theta_0,\quad H_1:\theta\ne\theta_0.$$

1. 先求出 $\theta$ 的置信水平为 $1-\alpha$ 的置信区间 $(\underline{\theta},\overline{\theta})$.

2. 判断 $\theta_0$ 是否落在 $(\underline{\theta},\overline{\theta})$ 中.若 $\theta_0\in(\underline{\theta},\overline{\theta})$，则接受 $H_0$. 反之，拒绝 $H_0$.

   • 类似地，可以通过求以上假设检验问题的拒绝域来求得 $\theta$ 的 $1-\alpha$ 置信区间.

---

小结

• 理解两类错误和两类风险
  
  • 假设检验原则：$P\left\{\text{拒绝}H_0\bigg|H_0\text{为真}\right\}\leq\alpha$
• 假设检验的一般步骤
  
  • 提出假设、选择统计量、给出拒绝域、作出判断

---

The scientist only imposes two things, namely truth and sincerity, imposes them upon himself and upon other scientists.
--Erwin Schrödinger