第八讲 二项分布与 Poisson 分布

概率论与数理统计 讲义 NUDT 2023SP

---

---

8.1 二项随机变量与二项分布

满足以下条件的随机试验称为 二项试验 (binomial experiment)

1. 由 $n$ 个小的试验构成，其中 $n$ 给定;
2. 每个小的试验均为 Bernoulli 试验，且概率分布相同;

3. 每个小的试验相互独立.

   • 二项试验：有限多个独立同分布的 Bernoulli 试验构成的随机试验.

---

例：二项试验

以下哪些试验可以视为二项试验？

1. 一个战士向同一目标进行多次射击，记录每次射击命中的环数.
2. 一群战士向同一目标进行射击，每次射击只记录是否命中.
3. 袋中装有一定数量的红球和黑球，每次摸出一球，记录球的颜色.
4. 从生产线上随机抽取产品进行检验，记录检验结果是否合格.

---

参考解答：

1. 不是. 二项试验只关注是否命中.
2. 不是，除非每个战士的命中率和射击状态完全一致.
3. 如果是无放回，不是；如果有放回，则是的.
4. 在同一批次中抽检，通常认为是的. 普通批次，或者如果持续不断地抽检（抽检总数不断增加），则不是.

---

二项分布

设 rv $X$ 表示二项试验中某个结果出现的次数，则 $X$ 称为一个二项随机变量

• 假设在每次 Bernoulli 试验中所关心的结果出现的概率为 $p$.
• 记号: $X\sim b(n,p)$ 或 $X\sim \text{Bin}(n,p)$.
• $X$ 的 pmf：$b(x;n,p)=\left\{\begin{array}{cl}C_n^xp^x(1-p)^{n-x}& x=0,1,\ldots,n\\ 0& \text{其他}\end{array}\right.$

---

二项 rv 的期望和方差

定理 若 $X\sim b(n,p)$, 则

• $E(X)=np$
• $D(X)=np(1-p)$

---

证：

• $E(X)=\sum\limits_{x=0}^{n}xb(x;n,p)=\sum\limits_{x=0}^{n}xC_n^xp^x(1-p)^{n-x}$
  
  • $=n\sum\limits_{x=1}^{n}C_{n-1}^{x-1}p^x(1-p)^{n-x}$
  • $=np\sum\limits_{x=1}^{n}C_{n-1}^{x-1}p^{x-1}(1-p)^{(n-1)-(x-1)}$
  • $=np\sum\limits_{i=0}^{n-1}C_{n-1}^ip^{i}(1-p)^{(n-1)-i}=np$

---

• $E(X^2)=\sum\limits_{x=0}^{n}x^2b(x;n,p)=\sum\limits_{x=0}^{n}[x(x-1)+x]C_n^xp^x(1-p)^{n-x}$
  
  • $=\sum\limits_{x=0}^{n}x(x-1)C_n^xp^x(1-p)^{n-x}+\sum\limits_{x=0}^{n}xC_n^xp^x(1-p)^{n-x}$
  • $=n(n-1)\sum\limits_{x=2}^{n}C_{n-2}^{x-2}p^x(1-p)^{n-x}+np$
  • $=n(n-1)p^2\sum\limits_{x=2}^{n}C_{n-2}^{x-2}p^{x-2}(1-p)^{(n-2)-(x-2)}+np$
  • $=n(n-1)p^2\sum\limits_{i=1}^{n-2}C_{n-2}^{i}p^{i}(1-p)^{(n-2)-i}+np$
  • $=n(n-1)p^2+np$
• $D(X)=E(X^2)-[E(X)]^2=n(n-1)p^2+np-n^2p^2=np(1-p)$

---

8.2 Poisson 分布

如果 rv $X$ 具有如下的 pmf，则称之为一个 Poisson 随机变量

$$p(x;\mu)=\mathrm{e}^{-\mu}\frac{\mu^x}{x!},\;x=0,1,2,\ldots$$

• $X$ 的分布称为参数为 $\mu (\mu>0)$ 的 Poisson 分布
  
  • 记为：$X\sim P(\mu)$

---

二项分布的 Poisson 近似

定理 如果 $n\to\infty$ 且 $p\to 0$ 的过程中，$np$ 趋近于常数 $\mu$，则

$$b(x; n, p)\to p(x; \mu).$$

• 记 $n p_{n}=\mu_{n}, p_{n}=\mu_{n} / n$
• $C_{n}^{k} p_{n}^{k}\left(1-p_{n}\right)^{n-k}=C_{n}^{k}\left(\frac{\mu_{n}}{n}\right)^{k}\left(1-\frac{\mu_{n}}{n}\right)^{n-k}$
  
  • $=\frac{\mu_{n}^{k}}{k !}\underbrace{1 \cdot\left(1-\frac{1}{n}\right) \cdot\left(1-\frac{2}{n}\right) \cdots\left(1-\frac{k-1}{n}\right)}_{k\text{项，每项均趋于}1}\underbrace{\left(1-\frac{\mu_{n}}{n}\right)^{n}}_{\text{趋于}\mathrm{e}^{-\mu}}\underbrace{\left(1-\frac{\mu_{n}}{n}\right)^{-k}}_{k\text{项，每项均趋于}1}$

---

---

---

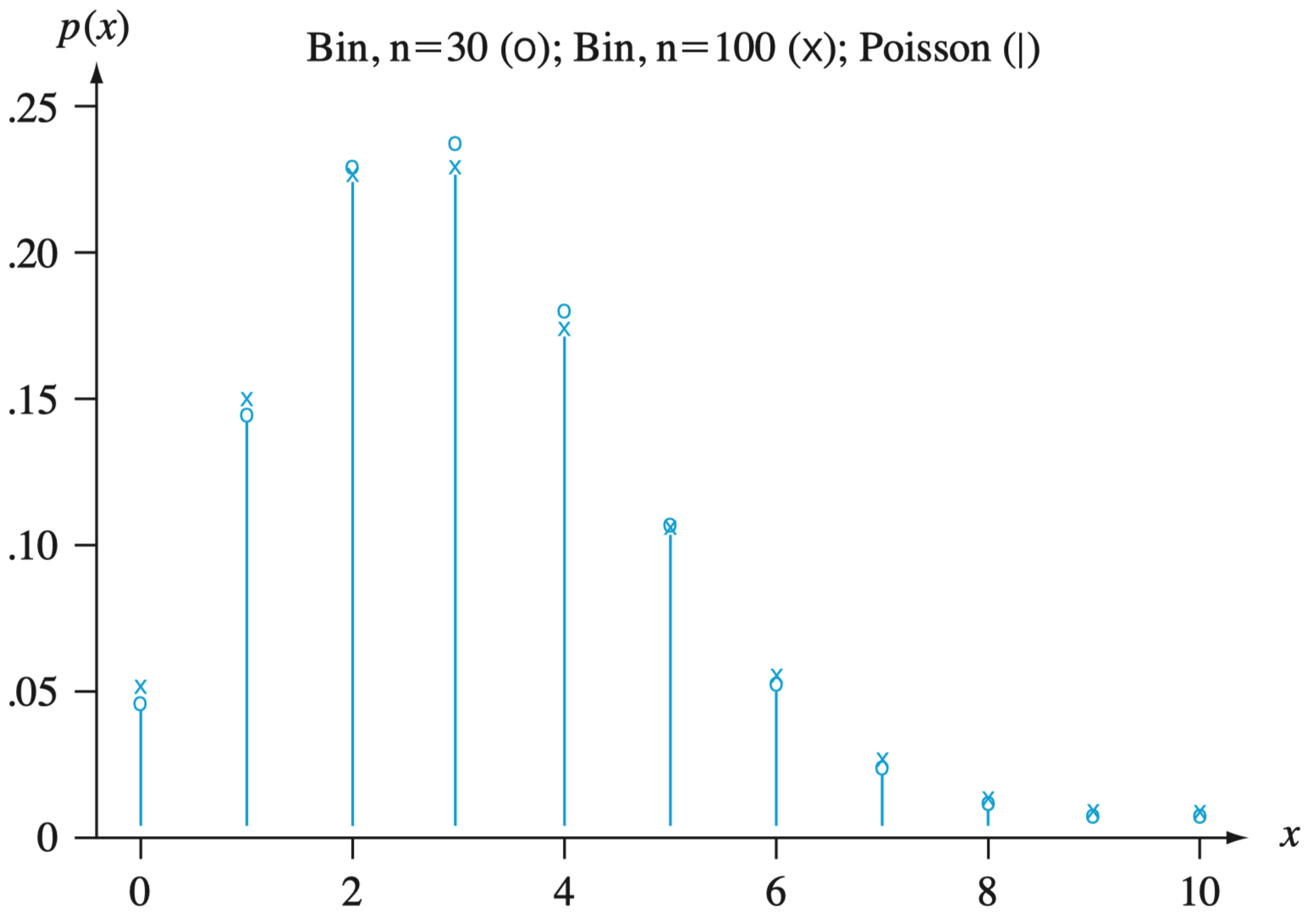
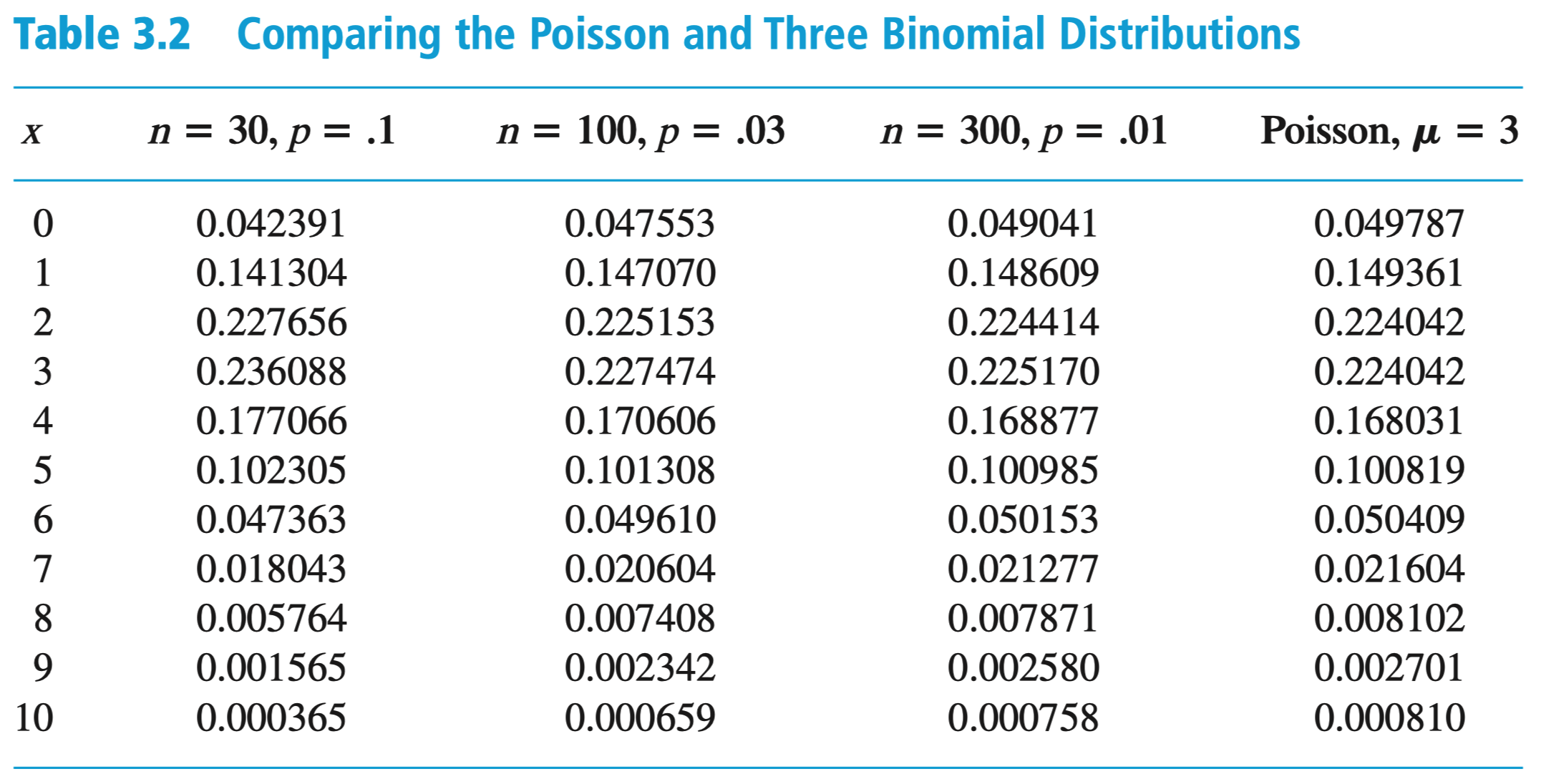
例：参保者死亡人数的估计

假设某项保险的投保者年死亡率为 $0.005$, 且当前有 $1,000$ 人参保. 试估计下一年度有关的如下概率：

（1）有 $10$ 位参保者死亡的概率;

（2）参保者死亡人数不超过 $5$ 的概率.

---

解：

• 记 rv $X=$ 下一年度参保者的死亡人数.
• 不妨设 $X\sim b(1000,0.005)$
• $P\{X=10\}=C_{1000}^{10} \times 0.005^{10} \times 0.995^{980}$
  
  • $\approx p(10;5)=\mathrm{e}^{-5}\frac{5^{10}}{10!} \approx 0.0181$
• $P\{X \leq 5\}=\sum_{k=0}^{5} C_{1000}^{k} \times 0.005^{k} \times 0.995^{1000-k}$
  
  • $\approx\sum_{k=0}^{5}p(k;5)\approx 0.616$

---

Poisson rv 的期望与方差

定理 设 rv $X\sim P(\mu)$, 则

$$E(X)=D(X)=\mu.$$

---

证：

• $E(X)=\sum\limits_{x=0}^{\infty}x\mathrm{e}^{-\mu}\frac{\mu^x}{x!}$
  
  • $=\sum\limits_{x=1}^{\infty}\mathrm{e}^{-\mu}\frac{\mu^x}{(x-1)!}=\mathrm{e}^{-\mu}\mu \sum\limits_{x=1}^{\infty}\frac{\mu^{x-1}}{(x-1)!}$
  • $=\mathrm{e}^{-\mu}\mu \sum\limits_{i=0}^{\infty}\frac{\mu^{i}}{i!}=\mathrm{e}^{-\mu}\mu \mathrm{e}^{\mu}=\mu$

---

• $E(X^2)=\sum\limits_{x=0}^{\infty}x^2\mathrm{e}^{-\mu}\frac{\mu^x}{x!}=\sum\limits_{x=0}^{\infty}[x(x-1)+x]\mathrm{e}^{-\mu}\frac{\mu^x}{x!}$
  
  • $=\sum\limits_{x=0}^{\infty}x(x-1)\mathrm{e}^{-\mu}\frac{\mu^x}{x!}+\sum\limits_{x=0}^{\infty}x\mathrm{e}^{-\mu}\frac{\mu^x}{x!}$
  • $=\mathrm{e}^{-\mu}\mu^2\sum\limits_{x=2}^{\infty}\frac{\mu^{x-2}}{(x-2)!}+\mu$
  • $=\mathrm{e}^{-\mu}\mu^2\sum\limits_{i=0}^{\infty}\frac{\mu^{i}}{i!}+\mu=\mathrm{e}^{-\mu}\mu^2 \mathrm{e}^{\mu}+\mu=\mu^2+\mu$
• $D(X)=E(X^2)-[E(X)]^2=\mu$

---

Poisson 过程

随时间出现的特定事件形成的随机现象，观察该事件在一段时间内出现的次数，例如：[1]

1. 一个小时内某个网站接到的访问请求数；
2. 每个月内某个银行服务台接待的客户数；
3. 一天之内某个邮箱收到的邮件数；
4. 半年时间内某个工业设施中随机出现的故障数；
5. 30 天时间内某天文台探测到的宇宙高能粒子数.

---

Poisson 过程的概率描述

定理 在给定的时间间隔 $t$ 内，某个 Poisson 过程中事件出现的次数是一个参数为 $\mu=\alpha t$ 的 Poisson rv.

• 注： 单位时间内事件出现次数的期望值为 $\alpha$ (Poisson 强度)，则时间间隔 $t$ 内事件出现次数的期望值为 $\alpha t$.
• 记 $P_k(t)$ 为时间间隔 $t$ 内事件出现 $k$ 次的概率，则
  
  • ${P_k(t)=\mathrm{e}^{-\alpha t}\frac{(\alpha t)^k}{k!}.}$

---

Poisson 过程的性质

• 任意有限区间内的出现次数均服从 Poisson 分布（但参数可能不同）.
• 任意两个不相交的区间内的出现次数彼此相互独立.
• 任意形如 $(t+a,t+b]$ 的区间内的出现次数只与 $b-a$ 有关.

---

Poisson 过程的性质

• 任意有限区间内的出现（到达）数量均服从 Poisson 分布（但参数可能不同）.
• 任意两个不相交的区间内的出现（到达）数量彼此相互独立.
• 任意形如 $(t+a,t+b]$ 的区间内的到达数量只与 $b-a$ 有关.

---

例：随机到达的脉冲信号

已知某个计数器记录下的脉冲信号数量约为每分钟 $6$ 次，求长度为半分钟的时间内最少有一次脉冲达到的概率.

• 假设脉冲信号的到达是一个 Poisson 过程. 由已知 $\alpha=6$.
• 长度为 $t=0.5$ 分钟的区间内的到达数量服从参数为 $\alpha t=3$ 的 Poisson 分布.
• 记 $X$ 为半分钟内到达的脉冲数量，则 $X\sim P(3)$.
• 所求概率为 $P\{X\geq 1\}=1-P\{X=0\}=1-\mathrm{e}^{-3}\frac{3^0}{0!}\approx 0.95$

---

平面上的 Poisson 分布

走入一片森林所在的区域 $R$ ，统计其中的树（🌲）的数量.

• 每棵树可以视为在平面区域的某个位置上发生的一个事件.
• 与按时间分布的 Poisson 过程类似，可以假设在区域 $R$ 内树木的出现呈现某种 Poisson 分布，其参数为 $\alpha\cdot a(R)$
  
  • 其中 $a(R)$ 为区域 $R$ 的面积.
  • $\alpha$ 表示单位面积内树木数量的期望.

---

8.3 超几何分布

从包含 $M$ 个红球和 $N-M$ 个黑球的袋中无放回地取出 $n$ 个球，记 $X$ 为 $n$ 个球中红球的个数.

• $X$ 的分布称为超几何分布 (hypergeometric distribution)，记为 $X\sim H(n,M,N)$
• $P\{X=k\}=\frac{C_M^kC_{N-M}^{n-k}}{C_N^n}$
  
  • 其中 $\max\{0,n-N+M\}\leq k\leq\min\{n,M\}$
• $E(X)=n\cdot\frac{M}{N}$，$D(X)=\frac{N-n}{N-1}\cdot n\cdot\frac{M}{N}\cdot\left(1-\frac{M}{N}\right)$

---

8.4 负二项分布

不断重复参数为 $p$ 的 Bernoulli 试验，记 $N$ 为直到第 $r$ 次成功所需要的试验次数.

• $N$ 的分布称为负二项分布(negative binomial distribution)，记为：$N\sim NB(r,p)$.
• $P\{N=k\}=C_{k-1}^{r-1}p^r(1-p)^{k-r},\;k=r,r+1,r+2,...$
• $E(N)=\frac{r}{p}$，$D(N)=\frac{r(1-p)}{p^2}$.
• $r=1$ 时，负二项分布退化为几何分布 $GE(p)$.

---

小结

• 需要重点掌握的三类离散型分布：0-1，二项，Poisson
• 二项分布
  
  • $b(x;n,p)=\left\{\begin{array}{cl}C_n^xp^x(1-p)^{n-x}& x=0,1,2,\ldots,n\\ 0& \text{其他}\end{array}\right.$
  • $E(X)=np$，$D(X)=np(1-p).$
• Poisson 分布
  
  • $p(x;\mu)=\mathrm{e}^{-\mu}\frac{\mu^x}{x!},\;x=0,1,2,3,\ldots$
  • $E(X)=D(X)=\mu.$

---

We are servants rather than masters in mathematics.
-- Charles Hermite

---

利用线性性计算期望值

定理 对随机变量 $X_1,X_2,...,X_n$ 和任意 $a_i\in\mathbb{R},i=1,2,...,n$,

$$E\left(\sum_{i=1}^na_iX_i\right)=\sum_{i=1}^na_iE(X_i).$$

进一步地，若 $X_1,X_2,...,X_n$ 相互独立，则

$$D\left(\sum_{i=1}^na_iX_i\right)=\sum_{i=1}^na_i^2D(X_i).$$

---

超几何分布的期望

从包含 $M$ 个红球和 $N-M$ 个黑球的袋中无放回地取 $n$ 个球，$X$ 为其中红球的个数.

• 记 $X=\sum\limits_{i=1}^nR_i$，其中 $R_i=\left\{\begin{array}{cl} 1,& \text{第}i\text{个摸到的是红球}\\ 0,& \text{第}i\text{个摸到的是黑球} \end{array}\right.,\;i=1,2,...,n.$
• $R_i\sim\begin{pmatrix} 1 & 0 \\ M/N & 1-M/N \end{pmatrix}$, 于是 $E(R_i)=\frac{M}{N}$.
• $E(X)=E\left(\sum\limits_{i=1}^nR_i\right)=\sum\limits_{i=1}^nE(R_i)=n\frac{M}{N}$.

---

例：匹配问题

共 $n$ 个人各取一顶帽子，求戴上了自己帽子的人数的期望.

• 记 $X=\sum\limits_{i=1}^nH_i$，其中 $H_i=\left\{\begin{array}{cl} 1,& \text{第}i\text{个人戴着自己的帽子}\\ 0,& \text{第}i\text{个人戴着别人的帽子} \end{array}\right.,\;i=1,2,...,n.$
• $H_i\sim\begin{pmatrix} 1 & 0 \\ 1/n & 1-1/n \end{pmatrix}$, 于是 $E(H_i)=\frac{1}{n}$.
• $E(X)=E\left(\sum\limits_{i=1}^nH_i\right)=\sum\limits_{i=1}^nE(H_i)=n\cdot\frac{1}{n}=1$.

---

负二项分布的期望

重复参数为 $p$ 的 Bernoulli 试验，记 $N$ 为直到第 $r$ 次成功所需要试验次数.

• 记 $N=\sum\limits_{i=1}^rN_i$，其中 $N_i$ 表示前一成功后直到下一次成功所需要再进行的试验次数, $i=1,2,...,r$.
• $N_i\sim GE(p)$，于是 $E(N_i)=\frac{1}{p}$.
• $E(N)=E\left(\sum\limits_{i=1}^rN_i\right)=\sum\limits_{i=1}^rE(N_i)=\frac{r}{p}$.

---

例：购物券的收集

• 某商场发行 $n$ 种购物券，每一次在该商场购物，即可获得一张种类随机选取的购物券.
• 该商场规定，如果能够收集齐所有的购物券，那么就可以得到该商场的大奖.
• 试问，平均需要进行多少次购物，才能获得大奖呢？

---

分析：

• 记 $N_i$ 为从获得第 $i-1$ 张购物券后到获得第 $i$ 张购物券需要的购物次数.
• 显然 $N_1=1$，$N_i\sim GE\left(\frac{n-i+1}{n}\right),\;i=2,3,...,n$.
• 获得所有购物券所需的总次数 $N=\sum_{i=1}^nN_i$.
• $E(N)=E\left(\sum_{i=1}^nN_i\right)=\sum_{i=1}^nE(N_i)=\sum_{i=1}^n\frac{n}{n-i+1}=n\sum_{i=1}^n\frac{1}{i}\approx n\ln n$.
• 聪明的商家： 当 $n$ 较大时，如果想收集到所有的购物券，则需要付出数倍于购物券数量的购物次数. (例如：$n=30$ 时 $\ln n\approx 3.4$ )