第十三讲 随机变量函数的分布

概率论与数理统计 讲义 NUDT 2023SP

---

---

复习回顾

• 概念
• 公式与方法
• 常用的概率分布
• 例题

---

概念

• 样本空间, 样本, 样本点数
• 事件, 互斥, 独立
• 概率的公理与性质
• 条件概率
• 随机变量
  
  • Bernoulli, 二项, Poisson
  • 均匀, 正态, 指数
• 概率分布: PMF, PDF, CDF, 分位点
• 期望, 方差

---

公式与方法

• 古典概型 $P(A)=\frac{n(A)}{n(\Omega)}$
  
  • 加法原理，乘法原理
  • 排列与组合
• 几何概型：$P(A)=\frac{\mu(A)}{\mu(\Omega)}$
• 乘法公式: $P(AB)=P(A|B)P(B)=P(B|A)P(A)$
• 全概率公式: $P(A)=\sum\limits_{k}P(A|B_k)P(B_k)$
• Bayes 公式: $P(A|B)=\frac{P(B|A)P(A)}{P(B)}$

---

• 期望与方差
  
  • 离散型 rv $X$, $E(X)=\sum_{x\in D}x\cdot p(x)$, $D(X)=\sum_{x\in D}(x-E(X))^2\cdot p(x)$
  • 连续型 rv $X$, $E(X)=\int_{-\infty}^{\infty}x\cdot f(x)\mathrm{d}x$, $D(X)=\int_{-\infty}^{\infty}(x-E(X))^2\cdot f(x)\mathrm{d}x$
• $D(X)=E(X^2)-\left[E(X)\right]^2$
• $E(aX+b)=aE(X)+b$
• $D(aX+b)=a^2D(X)$

---

• 当 $\lim\limits_{n\to\infty}np_n=\mu>0$ 是, $b(x;n,p_n)\to p(x;\mu)$
• 对离散型 rv $X$
  
  • $P(X=a)=F(a)-F(a-0)$
  • $E(h(X))=\sum_{x\in D}h(x)\cdot p(x)$
• 对连续性 rv $X$:
  
  • $P(X=a)=0$
  • $E(h(X))=\int_{-\infty}^{\infty}h(x)\cdot f(x)\mathrm{d}x$
• $p$ 分位点：$p=F(\eta(p))$

---

常用的随机变量

---

随机变量的函数

给定随机变量 $X$ 和函数 $g(\cdot)$, $Y=g(X)$ 也具有随机性，因此也是一个随机变量.

• 问题1： 求 $Y$ 的概率分布.
  
  • pmf/pdf
  • cdf
• 问题2： 求 $Y$ 的期望和方差.
  
  • $E(Y)$
  • $D(Y)$

---

13.1 离散型随机变量的函数

例：已知 rv $X$ 的 pmf 为

$$\begin{array}{ll} P\{X=-1\}=0.2, & \quad P\{X=0\}=0.3,\\ P\{X=1\}=0.1, & \quad P\{X=2\}=0.4 \end{array}$$

设 $Y=(X-1)^2$, 求 $Y$ 的 pmf.

---

解： 由已知

$$\begin{array}{c|cccc}\hline x & -1 & 0 & 1 & 2\\ \hline p_X(x) & 0.2 & 0.3 & 0.1 & 0.4 \\ \hline g(x) & 4 & 1 & 0 & 1\\ \hline \end{array}$$

故 $Y$ 的分布律为

$$\begin{array}{c|ccc}\hline y & 4 & 1 & 0\\ \hline p_Y(y) & 0.2 & 0.7 & 0.1\\ \hline \end{array}$$

---

求 g(X) 的 pmf

$$\begin{array}{c|ccccc} \hline x & x_1 & x_2 & \cdots & x_k & \cdots\\ \hline p_X(x) & p_1 & p_2 & \cdots & p_k & \cdots \\ \hline g(x) & g(x_1) & g(x_2) & \cdots & g(x_k) & \cdots\\ \hline \end{array}$$

• 列表给出 $Y$ 的所有取值
• 合并 $Y$ 的相同取值对应的表项，得到 $Y$ 的 pmf

---

13.2 利用连续型 rv 构造离散型 rv

例： 已知 rv $X\sim U(0,1)$, 令

$$Y=\left\{\begin{array}{l}{0, \quad 0<X \leq 0.25} \\ {1,\quad 0.25<X \leq 0.75} \\ {2,\quad 0.75<X<1}\end{array}\right.$$

求 $Y$ 的 pmf.

---

解：

$$\begin{array}{l} {P\{Y=0\}=P\{0<X \leq 0.25\}=0.25-0=0.25} \\ {P\{Y=1\}=P\{0.25<X \leq 0.75\}=0.75-0.25=0.50} \\ {P\{Y=2\}=P\{0.75<X<1\}=1-0.75=0.25} \end{array}$$

• 用计算机生成具有指定分布的离散随机数
  
  • 先生成某个连续区间内的伪随机数（pseudo random numbers），一般假设其服从该区间上的均匀分布
  • 将连续区间分段，每段对应一个离散值，每段长度占区间总长度的比例为取该离散值的概率
  • 根据生成的伪随机数所在的分段，将其映射为对应的离散值

---

13.3 连续型 rv 的函数

例： 已知 rv $X$ 的 pdf 为

$$f_{X}(x)=\left\{\begin{array}{ll} {\frac{x}{8}}, & 0<x<4 \\ {0}, & \text{其他} \end{array}\right.$$

求 $Y=2X+8$ 的 pdf.

---

解： $Y$ 的 cdf 为

$$\begin{aligned} F_{Y}(y) &=P\{Y \leq y\}=P\{2 X+8 \leq y\} \\ &=P\left\{X \leq \frac{y-8}{2}\right\}=F_{X}\left\{\frac{y-8}{2}\right\} \end{aligned}$$

于是

$$\begin{aligned} f_{Y}(y)&=\left\{\begin{array}{cl} \frac{1}{2} \cdot \frac{1}{8} \cdot \frac{y-8}{2}, &\quad 0<\frac{y-8}{2}<4 \\ 0 ,&\quad \text {其他}\end{array}\right.\\ &=\left\{\begin{array}{cl} \frac{y-8}{32}, &\quad 8<y<16 \\ 0 ,&\quad \text {其他}\end{array}\right. \end{aligned}$$

---

例： 设 rv $X$ 的 cdf 为 $F_X(x)$, $Y=5X-3$. 以下哪一个函数是 $Y$ 的 cdf

(A) $F_X(5y-3)$

(B) $5F_X(y)-3$

(C) $F_X\left(\frac{y+3}{5}\right)$

(D) $5F_X(y)$

---

单调函数的情形

定理： 已知连续型 rv $X$ 的取值范围 $D$ 和 pdf $f_X(x)$, 若函数 $g(x)$ 可微且严格单调，则 $g(x)$ 可逆 (设反函数为 $h(x)$ )，进而 $Y=g(X)$ 的 pdf 为

$$f_{Y}(y)=\left\{\begin{array}{cc}{\left|h^{\prime}(y)\right| \cdot f_{X}(h(y)),} & {h(y)}\in D \\ {0,} & {\text{其他}}\end{array}\right.$$

• 推论：在以上定理的条件下，$E(Y)=E(g(X))=\int_{-\infty}^{+\infty}g(x)f_X(x)\mathrm{d}x$

---

例： 已知 rv $X\sim U\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$, 求 $Y=\tan(X)$ 的 pdf.

• 记 $h(x)$ 为 $y=\tan x$ 的反函数.
  
  • $h(y)=\arctan y,\; h'(y)=\frac{1}{1+y^2},\;(y\in\mathbb{R})$
• $Y$ 的 pdf
  
  • $f_{Y}(y)=\left|h^{\prime}(y)\right| \cdot f_{X}(h(y))=\frac{1}{\pi} \cdot \frac{1}{1+y^{2}}$
    
    • 其中 $-\infty<y<\infty$
• 思考：如果改为 $X\sim U\left(0,\frac{\pi}{2}\right)$，结果有哪些边变化？

---

例： 已知 rv $X\sim U(0,1)$, 求 $Y=\mathrm{e}^X$ 的 pdf.

• $y>0$ 时, $y=\mathrm{e}^x$ 可逆，反函数 $h(y)=\ln y$.
  
  • 当$x\in[0,1]$ 时, $y=\mathrm{e}^x\in [1,\mathrm{e}]$.
• $Y$ 的 pdf 为
  
  • $f_{Y}(y)=\left\{\begin{array}{cc}\left|h^{\prime}(y)\right| \cdot f_{X}(h(y)),& \quad 1\leq y\leq \mathrm{e} \\ 0,& \text{其他} \end{array}\right.=\left\{\begin{array}{cc}\frac1y,& \quad 1\leq y\leq \mathrm{e} \\ 0,& \text{其他}\end{array}\right.$

---

对数正态分布

若 $\ln Y\sim N(\mu,\sigma^2)$，则称 $Y$ 服从参数为 $\mu,\sigma$ 的对数正态分布（logarithmic normal distribution）

• 密度：$\displaystyle f_Y(y)=\frac{1}{y\sigma\sqrt{2\pi}} \exp \left(-\frac{(\ln y-\mu)^2}{2\sigma^2} \right) I_{[0,\infty)}(y)$
• 期望：$\displaystyle E(Y)= \exp\left(\mu+\frac{\sigma^2}{2}\right)$
• 二阶矩：$\displaystyle E(Y^2)= \exp\left(2\mu+2\sigma^2\right)$
• 方差：$\displaystyle D(Y)=\exp\left(2\mu+\sigma^2\right)\left(\exp\left(\sigma^2\right)-1\right)$

---

利用对数变换观察数据的分布类型

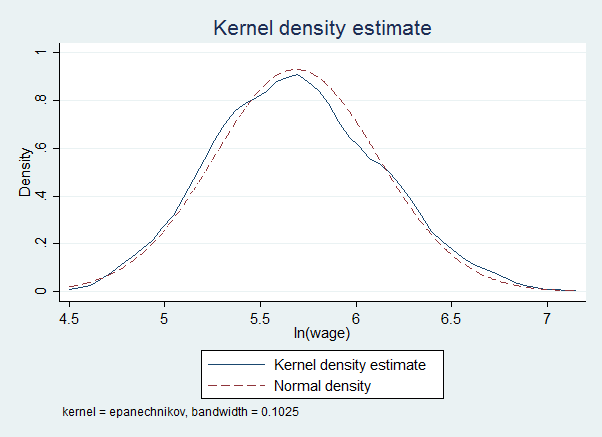
• 指数变换前 vs 指数变换后[1]

---

生成服从指定连续分布的随机数

任务：生成以 $F(x)$ 为 cdf 的随机数

• 不妨设 $F(x)$ 是连续且严格单调递增的, 则其存在反函数 $F^{-1}(y)$
• 设 $X\sim U(0,1)$，令 $Y=F^{-1}(X)$.
• $F_{Y}(y)=P\{Y\leq y\}=P\{X\leq F(y)\}=F(y)$
• 随机生成 $[0,1]$ 区间内的伪随机数 $x$，将其代入 $F^{-1}(x)$，即得到 cdf 为 $F(x)$ 的随机数

---

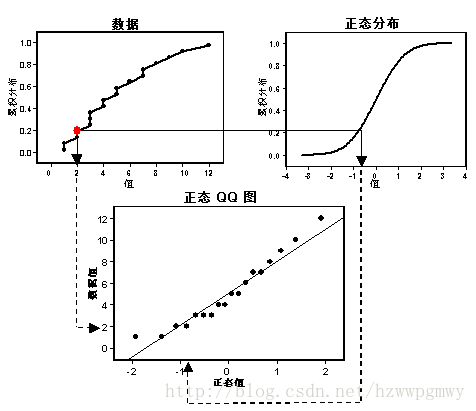
数据正态性的检验

定理：设连续型 rv $X$ 的 cdf $F(x)$ 可微且严格单调，则 $Y=F(X)\sim U(0,1)$.

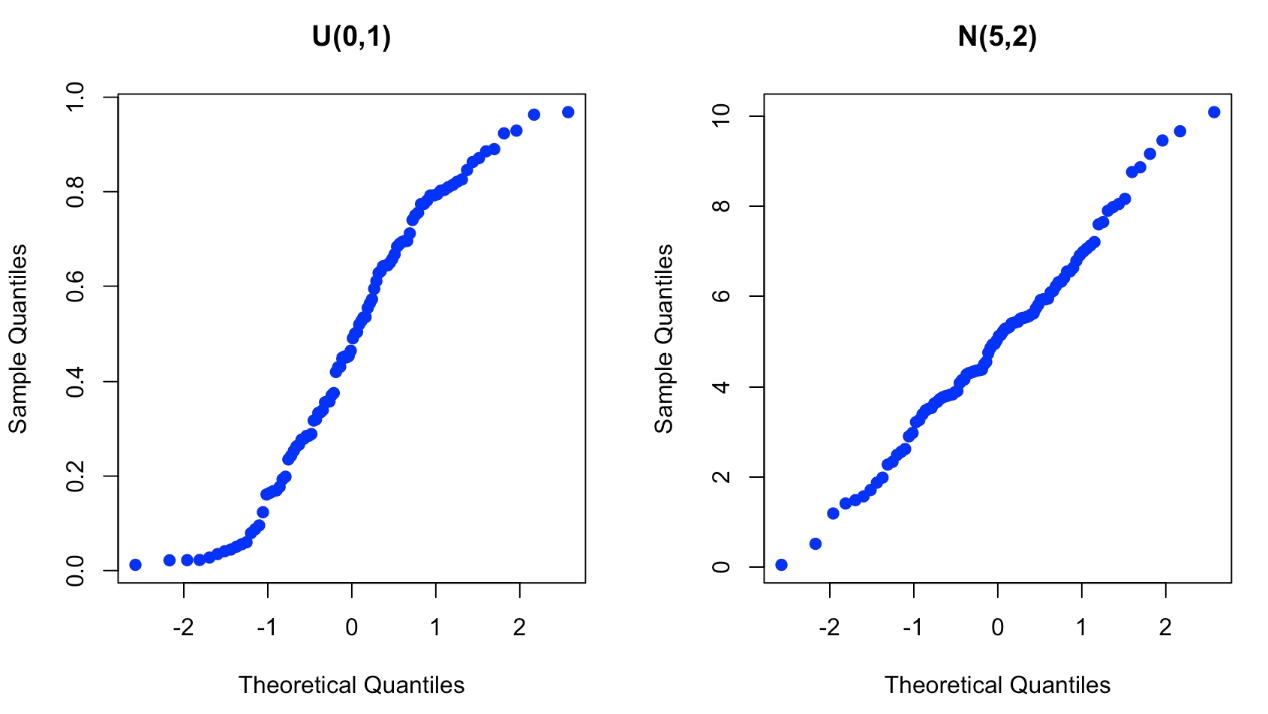
• 在 QQ 图(Quantile-Quantile Plot)[2]上，如果数据的分布接近于一条直线，则可以初步推断数据来源服从正态分布.
• 类似的方法也可以用于其他分布的初步检验以及对两组数据分布类型的比较

---

非单调函数的情形

定理：已知连续型 rv $X$ 的 pdf $f_X(x)$. 若在不相交的区间 $(a_k,b_k)\;(k=1,2,\ldots,n)$ 上, 函数 $g(x)$ 分段可微且严格单调，且值域均为 $(\alpha,\beta)$, 则 $g(x)$ 在每个小区间上均可逆 (反函数记为 $h_k(y)$), 进而 $Y=g(X)$ 的 pdf 为

$$f_{Y}(y)=\left\{\begin{array}{cc}{\sum\limits_{i=1}^n\left|h_{i}^{\prime}(y)\right| \cdot f_X\left(h_{i}(y)\right),} & {\alpha<y<\beta} \\ {0,} & {\text {其他}}\end{array}\right.$$

---

证明思路：以有三个单调区间的情况为例，

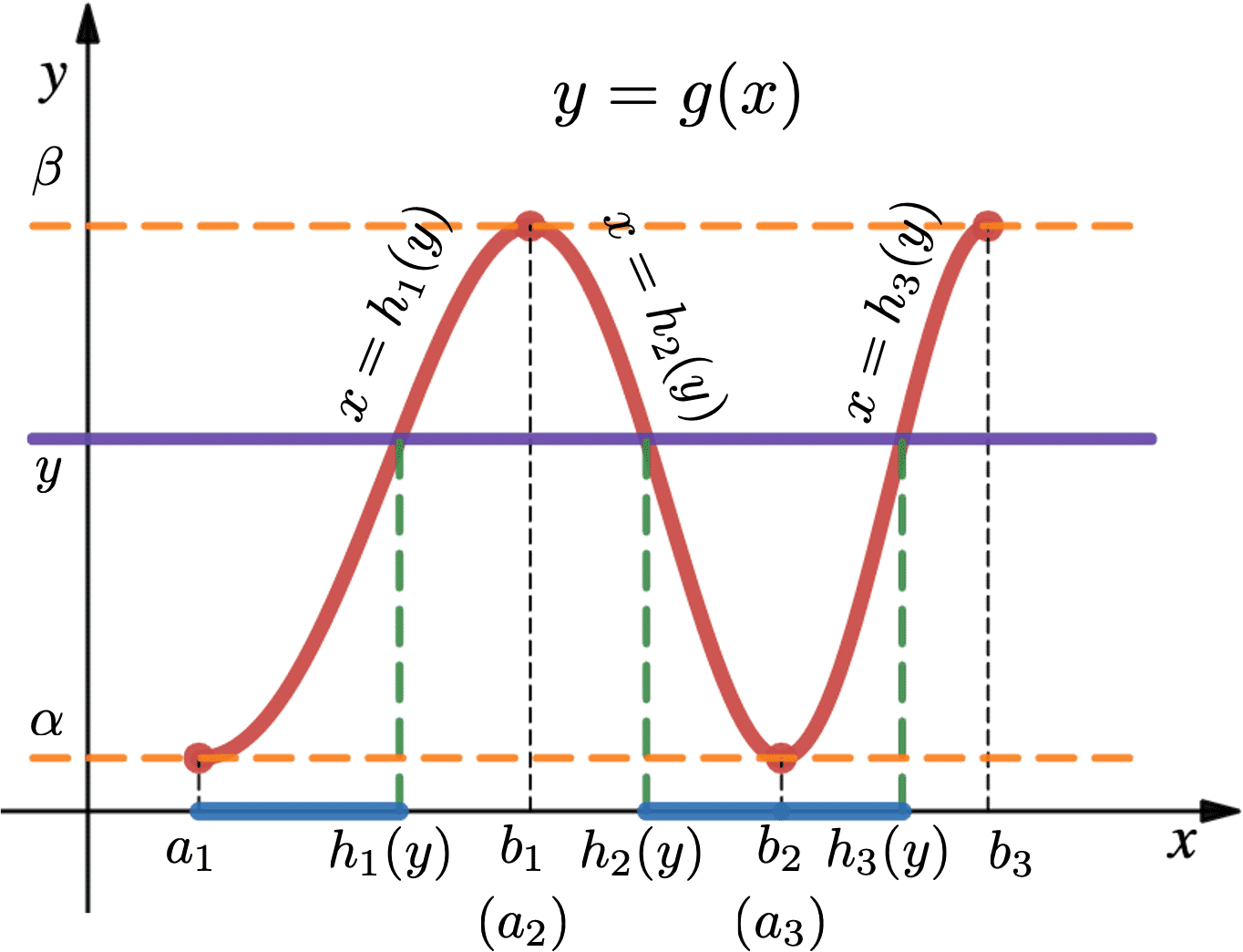
如图，

• $F_Y(y)=P\{Y\leq y\}$
  
  • $=P\{a_1\leq X\leq h_1(y)\}+P\{h_2(y)\leq X\leq b_2\}+P\{a_3\leq X\leq h_3(y)\}$
  • $=F_X(h_1(y))-F_X(a_1)+F_X(b_2)-F_X(h_2(y))+F_X(h_3(y))-F_X(a_3)$
• $f_Y(y)=\frac{\mathrm{d}}{\mathrm{d}y}F_Y(y)$
  
  • $=h_1'(y)f_X(h_1(y))-h_2'(y)f_X(h_2(y))+h_3'(y)f_X(h_3(y))$
  • $=\sum\limits_{i=1}^3|h_i'(y)|f_X(h_i(y))$

---

例： 已知 rv $X\sim N(0,1)$, 求 $Y=X^2$ 的 pdf.

• $g(x)=x^2$ 在 $(-\infty,0)$ 上严格单调递减，反函数为 $h_1(y)=-\sqrt{y}$, 在 $(0,\infty)$ 严格单调递增，反函数为 $h_2(y)=\sqrt{y}$
• $f_{Y}(y)=\left\{\begin{array}{cl}{\left|h_{1}^{\prime}(y)\right| f_X\left(h_{1}(y)\right)+\left|h_{2}^{\prime}(y)\right| f_X\left(h_{2}(y)\right),} & {y>0} \\ {0} & {y \leq 0}\end{array}\right.$
  
  • $=\left\{\begin{array}{cl}{\left|-\frac{1}{2 \sqrt{y}}\right| \frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{(-\sqrt{y})^{2}}{2}}+\left|\frac{1}{2 \sqrt{y}}\right| \frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{(-\sqrt{y})^{2}}{2}},}& y>0 \\ {0,} & {y \leq 0}\end{array}\right.$
  • $=\left\{\begin{array}{cl}{\frac{1}{\sqrt{2 \pi y}}\mathrm{e}^{-\frac{y}{2}}, }& y>0 \\ 0,& y \leq 0\end{array}\right.$

---

小结

给定 rv $X$ 和函数 $g(\cdot)$, 求 $Y=g(X)$ 的概率分布

• 若 $X$ 为连续型，且 $g$ 可微、严格单调
  
  • $f_{Y}(y)=\left\{\begin{array}{cc}{\left|h^{\prime}(y)\right| \cdot f_{X}(h(y)),} & {h(y)}\in D \\ {0,} & {\text{其他}}\end{array}\right.$
• 若 $X$ 为连续型，且 $g$ 可微、分段严格单调
  
  • $f_{Y}(y)=\left\{\begin{array}{cc}{\sum\limits_{i=1}^n\left|h_{i}^{\prime}(y)\right| \cdot f_X\left(h_{i}(y)\right),} & y\in D \\ {0,} & {\text {其他}}\end{array}\right.$
• $E(Y)= \int_{-\infty}^{+\infty} g(x)f_X(x) \mathrm{d} x$

---

Pure mathematics is, in its way, the poetry of logical ideas.
-- Albert Einstein

---

Rayleigh 分布

设 $X\sim\mathrm{Exp}(\lambda)$，则 $Y=\sqrt{X}$ 服从 Rayleigh 分布

• pdf: $\displaystyle f_Y(y)=\frac{2y}{\sigma^2}\exp\left(-\frac{y^2}{\sigma^2}\right)I_{[0,\infty)}(y)$，其中 $\sigma^2=\frac{1}{\lambda}$
• 期望、方差：$E(Y)=\frac{\sqrt{\pi}}{2}\sigma$, $D(X)=\left(1-\frac{\pi}{4}\right)\sigma^2$.
• Rayleigh 分布是实部、虚部均为 $N(0,\sigma^2)$ 的独立正态随机变量构成的复正态随机变量的模的分布.

---

Weibull 分布

设 $X\sim\mathrm{Exp}(\lambda)$，则 $Y=X^{1/\alpha}\;(\alpha>0)$ 服从 Weibull 分布.

• pdf: $f_Y(y)=\lambda\alpha y^{\alpha-1}\exp(-\lambda y^{\alpha})I_{[0,\infty)}(y)$
• 期望、方差： $E(X)=\lambda\Gamma\left(\frac{1}{\alpha}+1\right)$，$D(X)=\lambda\left[\Gamma\left(\frac{2}{\alpha}+1\right)-\left(\Gamma\left(\frac{1}{\alpha}+1\right)\right)^2\right]$
• Weibull 分布在可靠性研究总居于重要地位，其刻画了一种失效率为 $\displaystyle \frac{\alpha}{\lambda}\left(\frac{t}{\lambda}\right)^{\alpha-1}$ 的寿命的分布. $\alpha=1$ 时，Weibull 分布退化为指数分布.

---

Laplace 分布

设 $X\sim U(-1,1)$，则 $Y=-\lambda\mathrm{sgn}(X)\ln(1-|X|)$ 服从 Laplace 分布.

• pdf: $\displaystyle f_Y(y)=\frac{1}{2\lambda}\exp\left( -\frac{|y|}{\lambda} \right)$
• cdf: $\displaystyle F_Y(y)=\frac{1}{2}\left( 1-\exp\left(-\frac{|y|}{\lambda}\right)\right)+\frac{1}{2}I_{[0,\infty)}(y)$
• Laplace 分布适合描述所谓的“重拖尾”噪声，也即异常值（野值）较多的噪声.

---

Logistic 分布

设 $X\sim U(0,1)$，则 $\displaystyle Y=\mu+\beta\ln\frac{X}{1-X}$ 服从 Logistic 分布.

• pdf: $\displaystyle f_Y(y)=\frac{1}{\beta}\exp\left(\frac{y-\mu}{\beta}\right)\left(1+\exp\left(\frac{y-\mu}{\beta}\right)\right)^{-2}$
• cdf: $\displaystyle F_Y(y)=\frac{1}{2}\left[1+\tanh\left(\frac{y-\mu}{2\beta}\right)\right]$
• 由于 Logistic 函数的 $S$ 形状有很强的表现力，所以 Logistic 分布在诸多领域有着重要应用.

---

反正弦分布

设 $X\sim U(0,\pi/2)$，则 $Y=(\sin X)^2$ 服从反正弦分布.

• pdf: $\displaystyle f_Y(y)=\frac{1}{\pi\sqrt{y(1-y)}}I_{(0,1)}(y)$
• cdf: $\displaystyle F_Y(y)=\frac{2}{\pi}\arcsin\sqrt{y}I_{(0,1)}(y)$
• 反正弦分布式是 Beta 分布的特例，后者是定义在有限集合上的分布，其密度函数具有非常丰富的形状.

---

Pareto 分布

设 $X\sim \mathrm{Exp}(\lambda)$，则 $Y=\mathrm{e}^X$ 服从 Pareto 分布.

• pdf: $\displaystyle f_Y(y)=\lambda y^{-\lambda-1}I_{[1,\infty)}(y)$
• cdf: $\displaystyle F_Y(y)=1-y^{-\lambda}I_{[1,\infty)}(y)$
• Pareto 分布广泛用于描述资源（例如收入和财富）的分布，是微观经济学中最重要的概率分布之一.