第二讲 概率的定义和性质

概率论与数理统计 讲义 NUDT 2023SP

---

---

概率是什么？

• 英文: probability, likelyhood, chance, odd, ...
• 给定一个试验及其对应的样本空间 $\Omega$，概率就是为每个事件 $A$ 赋予一个实值 $P(A)$，称 $P(A)$ 为事件 $A$ 发生的概率 （简称：事件 $A$ 的概率）.
• 从数学的角度出发，概率是一个映射，将样本空间的子集映射为一个实数值.
  
  • 记 $\mathscr{F}$ 为 $\Omega$ 的子集所构成的 $\sigma$-代数，$\mathscr{F}$ 称为 $\Omega$ 上的 事件域 (Event field).
  • 对任意的 $A\in\mathscr{F}$, $P(A)\in\mathbb{R}$.
• 所谓 $\sigma$-代数，是指 $\mathscr{F}$ 中包含 $\Omega$ 且其 中的元素按照集合的补以及并可列的并运算封闭（若 $A_1,A_2,...\in\mathscr{F}$，则 $\bigcup\limits_{i=1}^{\infty}A_i\in\mathscr{F}$）.
  
  • 例如，$\{\varnothing,\Omega\}$ 就是 $\Omega$ 的子集构成的一个$\sigma$-代数.

---

2.1 概率的公理化定义

为了保证概率在定义上的无歧义，以及与直觉的一致性，数学上所说的概率需要满足以下公理. 同时，任何满足以下三条公理的函数 $P$ 均可称之为概率：

1. 非负性（Non-negativity）：对任意事件 $A$, $P(A)\geq0$.
2. 规范性 （Normativity）：$P(\Omega)=1$
3. 可数（列）可加性 （Countable additivity）：若 $A_1, A_2, A_3, ...$ 为无穷个互斥事件构成的序列，则 $P\left(\bigcup\limits_{i=1}^{\infty}A_i\right)=\sum\limits_{i=1}^{\infty}P(A_i)$

---

Andrey Kolmogorov(1903-1987)

link

• Soviet mathematician who made significant contributions to the mathematics of probability theory, topology, intuitionistic logic, turbulence, classical mechanics, algorithmic information theory and computational complexity, one of the greatest mathematicians of the twentieth century.
• In 1933, Kolmogorov published his book, Foundations of the Theory of Probability, laying the modern axiomatic foundations of probability theory.

---

概率的性质

1. $P(\varnothing)=0$.
2. 有限可加性：对于 $n$ 个互斥的事件 $A_1,\ldots,A_n$, $P\left(\bigcup\limits_{i=1}^{n}A_i\right)=\sum\limits_{i=1}^{n}P(A_i)$.
3. $P\left(\overline{A}\right)=1-P(A)$.
4. 单调性：若 $A\subset B$, 则 $P(A)\leq P(B)$.
5. 对于任意的事件 $A$, $0\leq P(A)\leq 1$.

---

和事件的概率

定理 对任意事件 $A,B$,

• $P(A-B)=P(A)-P(AB)$
• $P(A\cup B)=P(A)+P(B)-P(AB)$

---

例：能被 3 或 4 整除的数

随机抽取一个自然数，求该数能够被 $3$ 或 $4$ 整除的概率.

---

解： 记事件 $E_k$ 为能够被自然数 $k$ 整除，则 $P(E_k)=1/k,\;k=1,2,...$.

能够被 $3$ 或 $4$ 整除可表示为 $E_3\cup E_4$，其概率

$$P(E_3\cup E_4)=P(E_3)+P(E_4)-P(E_3\cap E_4).$$

注意到 $E_3\cap E_4=E_{12}$，也即同时被 $3$ 和 $4$ 整除等价于能够被 $12$ 整除，故 $P(E_3\cap E_4)=\frac{1}{12}=\frac1{12}$. 进而所求概率为

$$P(E_3\cup E_4)=\frac{1}{3}+\frac{1}{4}-\frac{1}{12}=\frac{1}{2}.$$

---

例（同时感染两种疾病的概率）

一个病人发着低烧来到医院. 经过检查，医生判断他要么是细菌感染，要么是病毒感染. 已知其为细菌感染的概率为 $0.7$，病毒感染的概率为 $0.4$，试问该病人同时为两种感染的可能性？

---

解: 令事件 $B,V$ 分别表示细菌感染和病毒感染.

已知 $P(B) = 0.7$, $P(V) = 0.4$ 且 $P(B\cup V)=1$. 需要计算 $P(B\cap V )$.

由前述定理，

$$P(B\cup V)=P(B)+P(V)-P(B\cap V),$$

故

$$1=0.7+0.4-P(B\cap V).$$

进而可知所求概率 $P(B\cap V)=0.1$.

---

多个事件和的概率

推论： 对于任意的三个随机事件 $A, B$, $C$,

$$\begin{aligned} P(A\cup& B\cup C)=P(A)+P(B)+P(C)\\ &-P(AB)-P(BC)-P(CA)+P(ABC) \end{aligned}$$

---

推论：对于任意 $n$ 个随机事件 $A_1, A_2,\ldots,A_n$,

$$\begin{aligned} &P(A_1\cup A_2\cup \ldots\cup A_n)\\ &\qquad= \sum\limits_{i=1}^nP(A_i)+(-1)^1\sum\limits_{i<j}P(A_iA_j)\\ &\qquad\quad +(-1)^2\sum\limits_{i<j<k}P(A_iA_jA_k)\\ &\qquad\quad +\ldots+(-1)^{n-1}P(A_1A_2\ldots A_n) \end{aligned}$$

---

2.2 概率的来源

---

公理化的概率

公理化的概率

• 概率所满足的公理保证了其在数学上的自洽（无歧义），但并未回答如何为具体的事件赋予概率值.
• 例如，抛硬币问题
  
  • 得到某一面的概率无法由概率的公理化定义得出.
  • 通常，人们习惯性地假定，每一面出现的概率相同.
  • 然而事实上，世界上找不到任何一枚两面绝对对等的硬币.
  • 因此，类似 “字朝上的概率为 $1/2$” 这样的说法，更多地来源于对现实观察的近似或为方便讨论而做出的假设.
• 如果抛的不是硬币，而是图钉呢？

---

频率

• 对同一事件发生的频数进行统计，进而得到其发生的频率（相对频数，relative frequencies），是定义其发生概率的一种常用方法.
• 例: 图钉落地后针头朝上（记为事件 $A$）的概率.
  
  • 重复进行 $N$ 次相同的试验，并且假设这些试验的环境完全相同，过程相互独立.
  • 记 $n(A)$ 为 $N$ 次试验中 $A$ 发生的次数.
  • 如果随着 $N$ 不断增大，$n(A)/N$ 趋于稳定,
    
    • 则定义 $P(A)=\lim\limits_{N\to\infty}\frac{n(A)}{N}$.

---

历史经验与主观信念

• 利用频率来得到概率，理论上可行，但实际中存在一些困难：
  
  • 不可能真正进行无穷多次试验，因此所得结果只能说是一种近似；
  • 每次试验不可能做到绝对的环境相同和互不干扰；
  • 有些试验的成本过于高昂，无法大量重复.
• 因此，大部分情况下我们所使用的概率，仍然包含假定的意味，或者说是人们基于历史经验而形成的某种主观信念.
• 例： 没有一个骰子是六面绝对均匀的，但我们通常假设每个数字出现的概率都是 $1/6$.

---

共识与约定

• 对于无法进行大量重复试验和不具有足够历史信息的情况，为了能够讨论相关的概率问题，人们常常基于约定或共识赋予一些特定事件发生的概率.
• 例如：
  
  • “明天很可能会下雨.”
  • “达成和平协议的概率很大.”
  • “发生 8 级以上地震的概率非常小.”
  • “物价发生大幅度上涨的可能性不大.”

---

小结：概率的来源/意义

• Limiting relative frequency from repeatable experiments.
  
  • 重复试验中的频率极限
• Bliefs about relative frequency of events.
  
  • 基于历史经验形成的认知
• Derived from prior information or subject opinions.
  
  • 主观的判断或共识

---

概率论究竟要做什么？

• 在给定某些事件的发生概率的前提下，计算与之相关的其他事件发生的概率.
• 概率论研究的核心问题：
  
  1. 利用给定的概率去推算更多的概率.
  2. 保证所得结果/结论在逻辑上的一致性.
• The interpretation of probability is something not involved with the theory of probability. （概率的意义，从来不是概率论所关心的问题）

---

2.3 等可能概型

---

同等无知原则

• Principle of Indifference: 如果没有更多的信息能够说明特定结果出现的概率更大，则可将所有可能结果出现的概率视为相同的.
• 例: 掷骰子(🎲)
  
  • 样本空间: $\Omega=\{1,2,3,4,5,6\}$, $n(\Omega)=6$
  • 事件 $A=\{\text{得到了偶数点}\}=\{2,4,6\}$,
    
    • $A$ 中的样本数：$n(A)=3$
  • 通常假设骰子是均匀的（六个面的地位对等）
    
    • 即：$P(\{i\})=1/6\;(i=1,2,\ldots,6)$.
  • $P(A)=P(\{2\})+P(\{4\})+P(\{6\})=\frac{n(A)}{n(\Omega)}=\frac12$

---

Bertrand 悖论

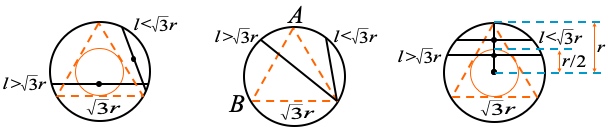
在给定的圆中任意作一条弦，求其弦长大于该圆内接正三角形的边长的概率,

$$p=P\{l>\sqrt{3}r\}.$$

---

• 解法 1: 假设弦中点取在圆内任意点处的概率是相同的.
  
  • $p = \frac { \pi ( r / 2 ) ^ { 2 } } { \pi r ^ { 2 } } = \frac { 1 } { 4 }$
• 解法 2: 假设弦的顶点取在圆上任意点出的概率是相同的.
  
  • $p=\frac{\text{arc length of }AB}{2\pi r}=\frac13$
• 解法 3: 假设弦中点取在圆半径上的任意位置的概率是相同的.
  
  • $p = \frac { r / 2 } { r } = \frac { 1 } { 2 }$
• 为什么同一个问题得到了不同的结果？
  
  • 因为最初的假设不同，而如何选择假设不是概率论所关注的问题！

---

小结

• 概率的公理化定义：理解可列可加性
• 事件和的概率计算公式
• 概率的来源/意义
• 同等无知原则与Bertrand 悖论

---

If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is.
-- John Louis von Neumann

---

Probabilistic方法：染色问题

• 设 $A$ 为平面上的一个点集，$A_1,A_2,...,A_n$ 为 $A$ 的子集，且满足 $n(A_i)=k,\;i=1,2,...,n$.
• 现考虑将 $A$ 中的点分别染成红色或蓝色.
• 证明：如果 $n<2^{k-1}$，则一定存在某种染色方案，使得每个 $A_i$ 中都至少包含一个红点和一个蓝点.

---

分析：

• 记样本空间 $\Omega$ 为所有染色方案构成的集合.
• 记事件 $B_i$ 为 $A_i$ 中的点全部被染成了蓝色或红色.
• $P(B_i)=\frac{2}{2^k}=\frac{1}{2^{k-1}},\;i=1,2,...,n$.
• 所有不满足要求的染色方案 $B=\bigcup\limits_{i=1}^nB_i$, 则 $P(B)\leq\sum\limits_{i=1}^nP(B_i)=\frac{n}{2^{k-1}}<1$.
• 这说明样本空间中一定存在不属于 $B$ 的元素，也即：存在满足要求的染色方案.

---

课堂讨论

可否提出一种概率模型，同时满足以下的条件：取样本空间 $\Omega=\mathbb{N}$，且：

1. 对任意 $k\in\mathbb{N}$，$P(\{k\})=0$.
2. $P(\Omega)=1$.

---

课后思考：为什么取偶数的概率正好是 1/2？

考虑任取一个自然数为偶数的概率，我们总是不假思索地说是 $1/2$. 但是细细一想，这个问题没有那么简单. 如果设样本空间为 $\Omega=\mathbb{N}$，那么其上的概率该如何定义呢？

• 如果对于任意的 $i\in\mathbb{N}$，$P(\{i\})=0$，那么由概率的可数可加性，不仅推出 $P(\text{偶数})=0$，甚至能推出 $P(\Omega) =0$, 岂不荒唐？
• 但是如果设 $P(\{i\})\ne 0$，岂不又有 $P(\Omega)=\infty$ 这样荒唐的结论？

你能否给出一个合理的概率模型，来说明任取一个正整数为偶数的概率为 $1/2$ 这样一个直观且明显的结论呢？