第十讲 博弈模型

数学建模 讲义 NUDT 2023SP

---

---

10.1 博弈论

• 博弈论（Game Theory）又称为 对策论 或 赛局理论，最初是经济学的一个分支.
• 1944 年，John von Neumann 与 Oskar Morgenstern 合著《博弈论与经济行为》（Theory of Games and Economic Behavior），标志著现代博弈理论的初步形成

---

博弈论的应用领域

• 博弈论的研究对象是多个具有自利（self-interested）特征的主体间的具有竞争或对抗性质的交互行为（博弈）
• 博弈论广泛应用于生物学、经济学、国际关系、计算机科学、政治学、军事战略领域
• 作为运筹学的一个重要分支，博弈论被认为是 20 世纪经济学最伟大的成果之一

---

博弈的要素

• 局中人/选手/参与者 (participate/player)：参与博弈的个人或团体
• 策略/对策 (strategy)：可供局中人选择的行动方案
• 效用/收益 (payoff)：局中人的收益或支出
• 信息：博弈的环境设定或博弈过程产生的信息
  
  • 在策略选择中，信息往往是最关键的因素
• 均衡：博弈的最终结果

---

符号约定

• 选手集： $N=\{1,2,\ldots, n\}$
• 策略集：$S_i$ 表示选手 $i$ 可选行为的集合 $(i=1,2,...,n)$
  
  • $x\in S_i$ 称为选手 $i$ 的一个策略
• 决策集： $D\subset S=S_1\times S_2\times\cdots \times S_n$
  
  • 所有选手的选择综合在一起构成了一个决策 $\boldsymbol{x}=(x_1,x_2,...,x_n)$
• 赢利函数： $f_i: D\to R,\; i=1,2,...,n.$
  
  • 赢利函数反映了不同决策对应的结果

---

田忌赛马

• $S_{\mbox{齐}}=S_{\mbox{田}}=\left\{\begin{array}{ccc}\text{（上中下）}, & \text{（中下上）}, & \text{（下上中）}, \\ \text{（上下中）}, & \text{（中上下）}, & \text{（下中上）}\end{array}\right\}$
• $f_{\mbox{齐}}( (\mbox{上中下}),(\mbox{下上中}))=0$，$f_{\mbox{田}}( (\mbox{上中下}),(\mbox{下上中}))=1$
• 双方若随机选取策略，则齐王有 5/6 的概率获胜，田忌只有 1/6.
• 在博弈过程中，每一方的“最佳策略”都必须依赖对方的“策略”选择.
• 博弈双方互相冲突又互相依赖，“我中有你，你中有我”.

---

帕累托最优

• 帕累托最优（Pareto Optimality）是经济学中的重要概念，是指资源（价值、收益）分配的一种理想状态.
• 帕累托改善 （Pareto Improvement）：从一种分配状态到另一种分配状态的迁移，使得至少有一人收益更大的同时，其他任何人的收益都没有减少
• 如果当前状态下不可能再有更多的帕累托改善，则称资源的分配达到了帕累托最优.
• 换句话说，帕累托最优状态下，不可能在不使任何其他人受损的情况下改善部分人的境况.

---

帕累托最优是否是绝对的理想状态？

• 严格来说，帕累托最优只是各种理想状态标准中的“最低标准”.
  
  • 如果一种状态尚未达到帕累托最优，那么还存在改进的余地.
• 现实中，改变的发展方向未必总是向着帕累托最优的方向进行.
• 达到了帕累托最优，也不一定真的很“理想”.
  
  • 例如，社会经济学认为，最求社会总财富最大化的过程中，常常可能导致社会公平性的缺失.

---

非合作博弈

• 参与者的理性行为：如果选手 $k$ 知道了所有其他选手的策略 $x_i\;(i\ne k)$，自然希望选择某个策略 $x_k\in S_k$，使得：
  
  • $f_k(\boldsymbol{x})=\max\limits_{y_k\in S_k} \left\{f_k(x_1,\ldots,y_k,\ldots,x_n)|(x_1,\ldots,y_k,\ldots,x_n)\in D\right\}$
• 选手 $k$ 的 合理反应集 为 $R_k=\left\{(x_1,\ldots,x_n)\in D|(x_1,\ldots,x_n)\mbox{使上式成立}\right\}$
  
  • 注意：$R_k$ 是所有选手决策的组合而不是某个选手的策略的集合，是在其他选手的策略都取定的前提下，对选手 $k$ 最有利的决策.
• 称 $\boldsymbol{x}\in R_1\cap \cdots \cap R_n$ 为该非合作博弈的 Nash平衡点/解（Nash Equilibrium）.

---

Nash定理

• Nash定理：非零和的非合作博弈一定存在 Nash 平衡点.
  
  • 零和 是指各方的收益总和为 0，非零和博弈才有可能实现共赢.
  • 如果决策不在 Nash 平衡点处，则博弈各方有调整策略的意愿，无法稳定.
  • 一旦到达 Nash 平衡点，则各方不会再轻易改变自己的策略，从而达到稳定.
• Nash平衡点可能不唯一.

---

John Forbes Nash Jr. (1928-2015)

• 美国数学家，主要研究博弈论、微分几何学和偏微分方程，曾就职于 MIT 和 Princeton 大学.
• 1950年，Nash 在仅仅 28 页的博士论文中提出了一个重要概念，成为博弈论中一项重要突破，这个概念被称为 “Nash 均衡”
• 1994年，他和其他两位博弈论学家 John Charles Harsanyi 和 Reinhard Selten 共同获得了诺贝尔经济学奖.

---

分钱游戏

• 两个人分 100 元钱，两人分别写下自己希望得到的数字 $x$ 与 $y$.
• 若 $x+y\leqslant 100$，则各自得到自己主张的钱数，否则，100 元充公.
• 问：该游戏的 Nash 均衡点是什么？
• 直观结论：$(50, 50)$ 是 Nash 均衡解.
• 一般结论：任意满足 $x+y=100$ 的 $(x,y)$ 都是 Nash 均衡解.

---

10.2 经典博弈模型

1. 囚徒困境
2. 智猪博弈
3. Braess 悖论
4. 旁观者效应

---

1. 囚徒困境

• 两名盗窃的同案犯因被发现藏有赃物而被捕，现被各自单独关押审讯.
• 两人都知道，如果依照被捕前约定，相互合作（cooperate），都不承认偷盗，将以窝赃罪各判 1 年监禁；
• 而如果彼此背叛（defect），都承认偷窃，将各判 5 年.
• 此外，如果一人坦白而另一人拒不交代，则坦白者从宽处理获得释放，拒不认罪者从严处罚判 10 年.
• 对这两个囚犯而言，最优的行动策略是什么？

---

分析

• 两位囚犯的策略集都是 $\{d(\mbox{招认}),c(\mbox{不招认})\}$，
• 盈利函数可表达为：$\boxed{\begin{array}{c|cc} 1\backslash 2 & \text{c} & \text{d}\\ \hline \text{c} & 1,1 & 10,0\\ \text{d} & 0,10 & 5,5 \end{array}}$
• 合理反应集分别为：$R_1=\{(d,d),(d,c)\}$, $R_2=\{(c,d),(d,d)\}$
• 所以对理性的囚犯而言，最优策略只有一个：$(d,d)$，即放弃合作，都选择坦白.

---

P2P 资源共享的囚徒困境

• 下载他人提供的资源，能够获得收益 $u$
• 为他人提供下载，要消耗自身的网络资源 $c$
• $\boxed{\begin{array}{c|cc} & \text{share} & \text{free-riding}\\ \hline \text{share} & u-c,u-c & -c,u\\ \text{free-riding} & u,-c & \bbox[yellow]{0,0} \end{array}}$
• 如果不对共享资源的行为给出足够的激励（补偿），抵消其消耗的成本，P2P 网络最终将因为 Free-Riding 的泛滥而最终走向资源枯竭

---

2. 智猪博弈

• 猪圈里有一头大猪，一头小猪.
• 猪圈的一头有一个食槽，另一头有一个控制猪食供应的按钮.
• 按一次按钮，会有 10 个单位的猪食入槽，但是按按钮者要付出 2 个单位的跑动成本，且可能会更晚到达食槽.
• 若大猪先到食槽，则大猪可吃到 9 个单位，小猪吃到 1 个单位；若两猪同时到达食槽，则为大猪 7 小猪 3；若小猪先到，则为大猪 6 小猪 4.
• 双方应该选择何种策略？

---

分析

• 大、小猪的策略集均为：$\{0\text{（不动）}，1\text{（按钮）}\}$
• 盈利函数可表示为 $\boxed{\begin{array}{c|cc} \mbox{大🐷\小🐷} & 1 & 0\\ \hline 1 & 5,1 & 4,4\\ 0 & 9,-1 & 0,0 \end{array}}$
• 大猪的合理反应集为：$\{(0, 1), (1, 0)\}$
• 小猪的合理反应集为：$\{(1, 0), (0, 0)\}$
• 所以最终的结果为：大猪按钮，小猪不动

---

企业的研发投入

• 在市场中，大企业和小企业类似智猪博弈中大猪和小猪的关系
• 按下按钮好比研发推出新产品，可以为所有企业带来附加利润，但研发者需要付出相当不菲的成本
• 对小企业而言，更理智的选择是“搭便车”，模仿大企业的产品，而大企业才是真正推动创新的主力

---

3. Braess 悖论

---

道路越多越通畅吗？

• 从出发点到 A 以及从 B 到终点这两条路，由于路况一般，所以通行时间和正在这条路上通行的车辆数量（$T$）有关，走完这两条路所需的时间均为 $T/100$
• 另外两段道路因为路况比较好，通行时间均是固定的 45 分钟
• 假设有 4000 辆车都准备从出发点行驶到终点，司机们应该选择经过 A 还是 B 的路呢？

---

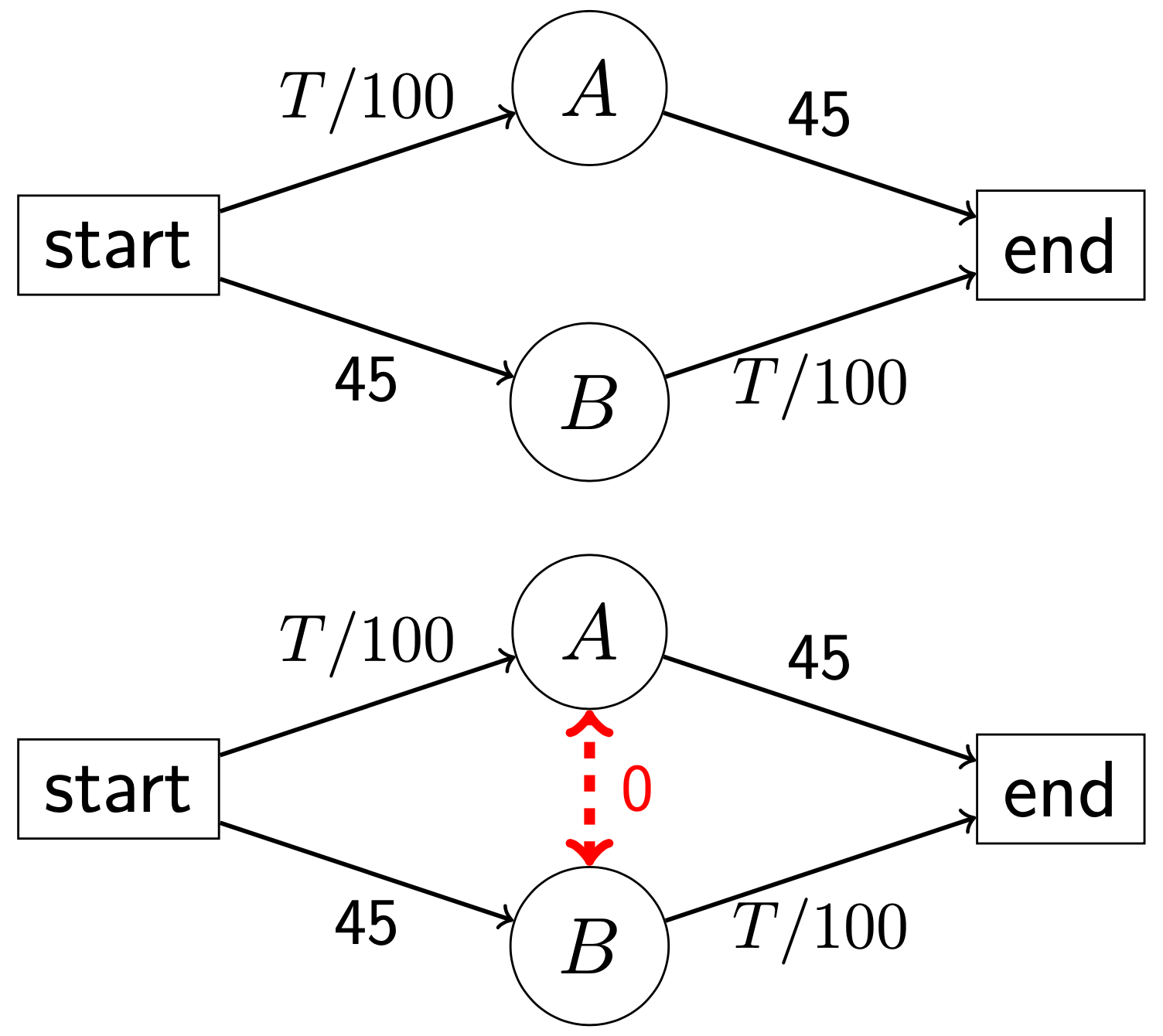
增加一条“捷径”

• 可以证明，没有其他捷径的情况下的 Nash 均衡点是两条路径上各 2000 辆车，此时两条路的通行时间都是 $2000/100 + 45 = 65$ 分钟
• 假设新路很短，通过时间可以忽略不计.
• 新的 Nash 均衡点：新路修好后所有司机最终都会选择“起点-A-B-终点”，通行时间是 $80$ 分钟.
• 研究发现，如果一个交通网络上每一条路的通行时间都与这条路上的车辆数量成线性关系，这个交通网络就一定存在一个 Nash 均衡点，它可能导致全体不利的情况发生，即出现 Braess 悖论 （Braess Paradox）.

---

真实案例：What if They Closed 42d Street and Nobody Noticed

• 1990.12.25 (世界地球日)，New York，关闭第 42 号大街.
• 许多人认为这一天将是灾难性的一天 (doomsday).
• 有趣的是，在当天纽约却并没有发生大塞车，交通状况反而难以置信的比平时有所好转.

---

弹簧模型

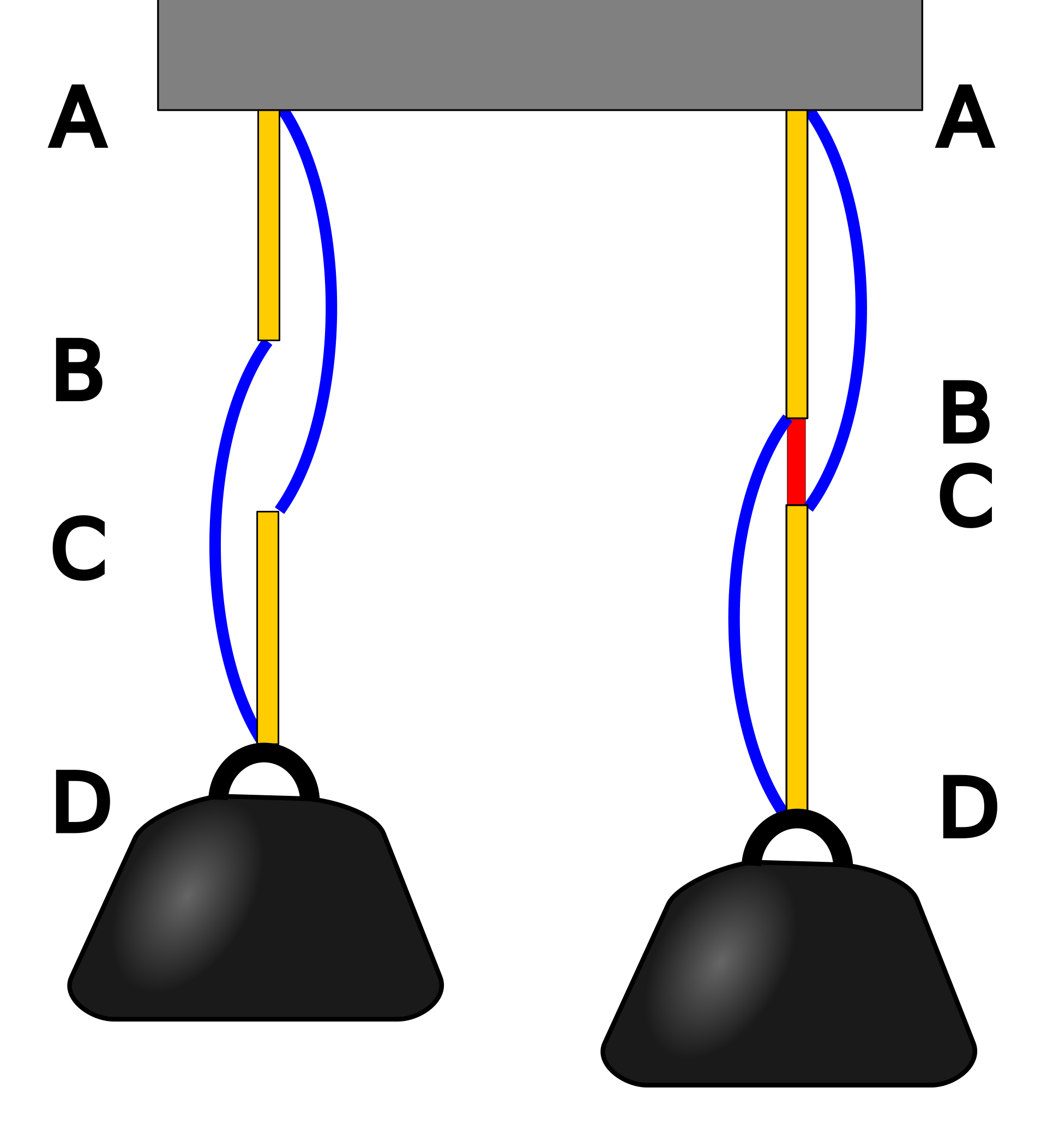
• 由短绳（红色）串联两个相同的弹簧（黄色），其总的弹力系数为单独弹簧的一半，导致在悬挂某个重物时有很长的拉伸.
• 增加两根较长的松弛绳（蓝色），然后切断短绳，此时长绳紧绷，两个弹簧变得相互平行，总的弹力系数是每个单独弹簧的两倍.
• 该模型在数学上与 Braess 悖论有着相同的结构.

---

4. 旁观者效应

• 1964 年 3 月 13 号凌晨 3 点，纽约市民 Kitty Genovese 在即将回到住处时，遭到持刀暴徒的袭击，她惊恐的尖叫并恳求帮助.
• 她的邻居中，有 37 人走到窗户前观望了片刻，目睹她在歹徒的伤害中挣扎，但直到歹徒离开，才有人打电话报警.
• Genovese 因未能得到及时救治死亡.

---

为什么围观者会见死不救？

• 大量的实验和研究显示在公共场所观看危机事件的旁观者越多，愿意提供帮助的人就越少.
• 当旁观者的数目增加时，任何一个旁观者都会更少地认为自己有采取行动的责任，这种现象被称为 旁观者效应 (Bystander Effect).

---

博弈论解释

• 假设：
  
  • 每个旁观者在事件中的地位是相同的
  • 有人提供帮助时，围观者每人可以获得固定收益（心理安慰）$a$
  • 提供帮助者会有损失（成本与风险） $b$

---

分析

• 任一人 A 的收益矩阵 $\boxed{\begin{array}{c|cc} & \text{其他人不帮助} & \text{有其他人帮助}\\ \hline \text{A不帮助} & 0 & a\\ \text{A帮助} & a-b & a-b \end{array}}$
• 假设共有 $n$ 个人，每个人不帮助的概率为 $p$，那么
  
  • A 不帮助的期望收益为 $Q_1=0\cdot p^{n-1}+a\cdot (1-p^{n-1})$
  • A 帮助的期望收益为 $Q_2=(a-b)\cdot p^{n-1}+(a-b)\cdot (1-p^{n-1})$

---

• 由全期望公式，A 的总预期收益为：
  
  • $Q(p)=p\cdot Q_1+(1-p)\cdot Q_2=a-b-ap^n+bp$
• 令 $\mathrm{d} Q(p)/\mathrm{d} p =0$ 解得 $p={\left(\dfrac{b}{na}\right)}^{\frac{1}{n-1}}$
• 可以验证，不帮助的概率 $p$ 随围观人数 $n$ 单调递增.

---

结论

• 围观者越多，围观者施以援手的愿望越低；
• 和谐社会，需要增加 $a$ 值以鼓励助人为乐，比如提供经济或者精神上的奖励.
• 和谐社会，需要降低 $b$ 值以减少助人为乐的成本或风险.

---

10.3 不完全信息静态博弈模型

• 完全信息博弈：每个参与人的特征、收益以及策略空间都是所有参与人的共同知识
  
  • 不完全信息博弈：至少上述信息之一不是共同知识
• 动态博弈：类似于回合制游戏，参与各方轮流作出决策，博弈过程一直持续
  
  • 静态博弈：各方的决策是同时作出的

---

市场扩张的博弈模型

企业甲、乙都了解对市场需求的情况，且企业甲了解企业乙的收益情况，但企业乙不知道企业甲的生产成本

$$\begin{matrix} \text{市场需求高（20%）}\\ \boxed{\begin{array}{c|cc} \text{甲\乙} & \text{扩张（K）} & \text{保持（B）}\\\hline \text{扩张（K）} & 3,2 & 5,1\\ \text{保持（B）} & 0,3 & 2,1 \end{array}} \end{matrix} \quad \begin{matrix} \text{市场需求低（80%）}\\ \boxed{\begin{array}{c|cc} \text{甲\乙} & \text{扩张（K）} & \text{保持（B）}\\\hline \text{扩张（K）} & -2,-2 & -1,0\\ \text{保持（B）} & 0,-1 & 2,1 \end{array}} \end{matrix}$$

---

贝叶斯纳什均衡解

• 由于存在不确定因素（市场需求），这时的 Nash 均衡解是指在期望收益最大条件下的策略组合，称为 贝叶斯纳什均衡解（Bayesian Nash Equilibrium）
• 企业甲的策略有：$a(K,K), b(K,B), c(B,B), d(B,K)$
  
  • $(K,K)$ 的含义为在市场需求高和低的状态下都选择扩张
• 企业乙由于不知道企业甲的所有信息，从而必须考虑甲采取的策略，故其策略为：$w(K/K,B/K), x(K/K,B/B),y(K/B,B/K),z(K/B,B/B)$
  
  • $w(K/K,B/K)$ 的含义为若甲扩张，则选择扩张，若甲保持，仍选择扩张.

---

预期收益

$$\boxed{\begin{array}{c|cccc} \text{甲\乙} & w\text{（冒险）} & x\text{（跟随）} & y\text{（反向）} & z\text{（保守）}\\ \hline a(K,K) & -1,-1.2 & -1,-1.2 & 0.2,0.2 & 0.2,0.2\\ b(K,B) & 0.6,-0.4 & \bbox[yellow]{2.2,1.2} & 1,-0.6 & 2.6,1\\ c(B,B) & 0,-0.2 & 2,1 & 0,-0.2 & 2,1\\ d(B,K) & -1.6,-1 & -0.6,0 & -1.2,-1.4 & -0.4,0.2 \end{array}}$$

• 唯一贝叶斯纳什均衡点 $(b,x)$，意味着甲乙双方都采取“高扩低保”的策略.

---

10.4 拍卖（招投标）模型

William Vickrey，1914-1996

• 美国经济学家
• 在信息经济学方面作出开创性研究
• 1996 年获诺贝尔经济学奖

---

典型的拍卖模型

• 最高价密封拍卖：
  
  • 每个竞买者可进行一次报价，报价密封后交予拍卖方，所有报价同时解封，出价最高者获得该拍品，按最高报价成交
• 次高价密封拍卖：
  
  • 每个竞买者可进行一次报价，报价密封后交予拍卖方，所有报价同时解封，出价最高者获得该拍品，按次最高报价成交

---

高价密封拍卖

• 有 $N$ 个竞拍人，第 $i$ 个竞拍人对标的的估价为 $v_i$，出价为 $b_i$
• 根据竞拍规则，竞拍人的收益 $u_i(\boldsymbol{v},\boldsymbol{b})=\begin{cases} v_i-b_i, & b_i=\max\limits_j b_j \\ 0, & \text{其他} \end{cases}$
• 竞拍人无法知道其他人的估价，但假设其他人的估价是区间 $[0,1]$ 上均匀分布的一个随机变量.
• 竞拍人的出价策略为 $b_i=\beta_i(v_i),\;i=1,...,N$，其中 $\beta_i$ 严格递增

---

两个参与者的情况

• $u_1(v_1,v_2,b_1,b_2)=\begin{cases} v_1-b_1, & b_2<b_1 \\ 0, & b_2>b_1 \end{cases}$
• $E_1=(v_1-b_1)P\{b_2<b_1\}=(v_1-b_1)P\{\beta_2(v_2)<b_1\}$
  
  • $=(v_1-b_1)P\{v_2<\beta_2^{-1}(b_1)\}=(v_1-b_1)\beta_2^{-1}(b_1)$
• 假设双方出价策略相同，即 $\beta_1=\beta_2$，于是参与者 1 的优化目标为
  
  • $\max E_1=(v_1-b_1)\beta^{-1}(b_1)$

---

最优策略

• 令 $\dfrac{\mathrm{d}E_1}{\mathrm{d}b_1}=0\quad\Rightarrow\quad -\beta^{-1}(b_1)+(v_1-b_1)\dfrac{\mathrm{d}\beta^{-1}(b_1)}{\mathrm{d}b_1}=0$
  
  • $\Rightarrow v_1=(v_1-b_1)\dfrac{\mathrm{d}v_1}{\mathrm{d}b_1}\quad\Rightarrow\quad b_1=\dfrac{v_1}{2}$
• 结论：仅有两个竞拍人的情形，此竞拍博弈模型的贝叶斯纳什均衡解是，每个竞拍人的出价是自己估价的一半

---

N 个竞拍人的情形

• $E_1=(v_1-b_1)\prod\limits_{j\ne 1}P\{b_j<b_1\}=(v_1-b_1)[\beta^{-1}(b_1)]^{N-1}$
• 求解最优化问题，解得 $b_1=\dfrac{N-1}{N}v_1$
• 结论：最高价成交 $N$ 人竞拍模型的贝叶斯纳什均衡解为：每个竞拍人按自己估价的 $(N-1)/N$ 出价
  
  • 参与竞价多人越多，参与者的最优出价就越接近于其估价.
• 对于次高价成交模型，贝叶斯纳什均衡解为：各竞拍方按各自的估价出价！

---

成交价的期望

• 最高价成交
  
  • $E\left(\max\limits_i\dfrac{N-1}{N}v_i\right)=\dfrac{N-1}{N}N\int\limits_{0<x_i<x_1<1\atop i>1}x_1\mathrm{d}x_1...\mathrm{d}x_N=\dfrac{N-1}{N+1}$
• 次高价成交
  
  • $E=N(N-1)\int\limits_{0<x_i<x_2<x_1<1\atop i>2}x_1\mathrm{d}x_2...\mathrm{d}x_N=\dfrac{N-1}{N+1}$

---

成交价的方差

• 最高价成交
  
  • $\sigma_1^2=\dfrac{(N_1)^2}{N(N+1)^2(N+2)}$
• 次高价成交
  
  • $\sigma_2^2=\dfrac{(N_1)^2}{2N(N+1)^2(N+2)}=2\sigma_1^2$
• 使用次高价成交最终成交价的波动可能更大.

---

课后思考题

（$\star\star$）推导次高价拍卖的成交价期望与方差的计算公式.