第四讲 条件概率与事件的独立性

概率论与数理统计 讲义 NUDT 2023SP

---

---

4.1 条件概率

对任意两个事件 $A$ 和 $B$，若 $P(B)\ne 0$, 则可定义 $B$ 发生的前提下 $A$ 发生的条件概率 (the conditional probability of $A$ given that $B$ has occurred) 为

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

---

例：猜硬币问题

甲抛两枚硬币，然后盖住落下的硬币，乙猜 “正反各有一次朝上”，乙猜对的概率是多少？

• 样本空间 $\Omega = \{ \mathrm {正正} , \mathrm {正反} , \mathrm {反正} , \mathrm {反反} \}$
• 记 $A=\{\text{正反各有一次朝上}\}= \{ \mathrm {正反} , \mathrm {反正} \}$，则 $P(A)=1/2$
• 如果丙透漏“至少出现了一次正面”的信息给乙，则乙猜对的概率又是多少？

---

分析： 由于乙获知 $B=\{\text{至少出现了一次正面}\}$，故样本空间变为

$$\Omega ^ { \prime } = \{ \mathrm { HH } , \mathrm { HT } , \mathrm { TH } \} = \Omega \cap B$$

所以 $P(A)=\frac23$

• 为什么会有不同的结果？
  
  • 解释： 概率空间不同，概率的值也不一样！
  • 后一个概率应该是 $P ( A | B ) = \frac { 2 / 4 } { 3 / 4 } = \frac { P ( A B ) } { P ( B ) }$

---

条件概率的性质

已知 $P(B)>0$, 可以验证

• 非负性：对任意事件 $A$, $P(A|B)\geq0$
• 规范性：$P(\Omega|B)=1$
• 可列可加性：
  
  • 若 $A_1, A_2, A_3, ...$ 为无穷多个互斥的事件,
  • 则 $P\left(\bigcup\limits_{i=1}^{\infty}A_i\bigg|B\right)=\sum\limits_{i=1}^{\infty}P(A_i|B)$
• 条件概率是概率！

---

4.2 乘法公式

$$P(A\cap B)=P(A|B)P(B)$$

• 推广：若 $P \left( A _ { 1 } A _ { 2 } \cdots A _ { n } \right) > 0$，则
  
  • $P(A_1A_2...A_n)=P \left( A _ { 1 } \right) P \left( A _ { 2 } | A _ { 1 } \right) P \left( A _ { 3 } | A _ { 1 } A _ { 2 } \right)\cdots P \left( A _ { n } | A _ { 1 } A _ { 2 } \cdots A _ { n - 1 } \right)$
• 乘法公式：将事件同时发生的概率转化为按一定次序发生的事件的概率的乘积

---

例： 四个人参加义务献血. 因为之前没有献过血，所以他们的血液类型都是未知的. 假设当前只需要型 O 型血，且已知四人中只有一个是 O 型。 如果四个人按照随机的顺序验血，求至少需要检查三个人才能找到 O 型血捐献者的概率？

---

解：

• 定义事件：$B=\{\text{第一个人不是 O 型}\}$, $A=\{\text{第二个人不是 O 型}\}$.
• 由已知 $P(B)=\frac34$.
• 如果已知第一个人不是 O型, 则剩下三人中还有两人不是 O 型，从而 $P(A|B)=\frac23$.
• 由乘法公式
  
  • $P(\text{至少需要检验三人才能找到 O 型捐献者})$
    
    • $=P(A\cap B)=P(A|B)P(B)=\frac23\cdot\frac34=0.5$

---

思考: 在以上的例子中，$P(A)=?$

• $P(A)$ 的含义是什么？
  
  • 在不确定其他人血型的情况下，第二个人的血型不是 O 型的概率.
• $P(A|B)$ 的含义是什么？
  
  • 在已知第一个人不是 O 型的情况下，第二个人不是 O 型的概率.

---

例：摸球问题

袋中有 $r$ 个红球和 $b$ 个黑球. 所有的球外形和材质完全相同. 无放回地依次从袋中取出两个球，计算两个都是红球的概率.

• $P(\text{两个都是红})$
  
  • $=P(\text{第一个红，且第二个红})$
  • $=P(\text{第一个红})P(\text{第二个红}|\text{第一个红})$
  • $=\frac{r}{r+b}\frac{r-1}{r+b-1}$

---

例：某球队要经过三轮比赛才能出线。该球队第一轮比赛被淘汰的概率为 $0.5$，第二轮比赛被淘汰的概率为 $0.7$，第三轮比赛被淘汰的概率为 $0.9$，求球队出线的概率。

---

解：记 $A_i=\{\text{球队第 i 轮被淘汰}\},i=1,2,3$，则

$$\begin{aligned} P\{\text{球队出现}\} & = P \left( \overline { A } _ { 1 } \overline { A } _ { 2 } \overline { A } _ { 3 } \right) \\ & = P \left( \overline { A } _ { 3 } | \overline { A } _ { 1 } \overline { A } _ { 2 } \right) P \left( \overline { A } _ { 1 } \overline { A } _ { 2 } \right) \\ & = P \left( \overline { A } _ { 3 } | \overline { A } _ { 1 } \overline { A } _ { 2 } \right) P \left( \overline { A } _ { 2 } | \overline { A } _ { 1 } \right) P \left( \overline { A } _ { 1 } \right) \\ & = ( 1 - 0.9 ) ( 1 - 0.7 ) ( 1 - 0.5 ) \\ & = 0.015 \end{aligned}$$

---

4.3 事件的独立性

• 称两个事件 $A,B$是 相互独立的（independent），当且仅当
  
  • $P(A|B)=P(A)$,
  • 或 $P(B|A)=P(B)$.
• 命题: 事件 $A,B$ 相互独立，当且仅当二者不相容？
  
  • 错！
  • $A,B$ 不相容（互斥），则不相互独立！

---

定理: $A$，$B$ 相互独立，当且仅当

$$P(AB)=P(A)P(B).$$

• 讨论: 如果事件 $A$，$B$ 相互独立，以下哪些事件相互独立：
  
  • $A$ 与 $\overline{A}$
  • $A$ 与 $\overline{B}$
  • $\overline{A}$ 与 $\overline{B}$
• 除了第一组，后面两组都相互独立！

---

多个事件的独立性

称事件 $A_1, ... , A_n$ 称为 相互独立的（mutually independent），是指：对任意 $(k=2,\ldots,n)$ 和 $1\leq i_1<...< i_k\leq n$,

$$P\left(\bigcap_{i=1}^kA_{i_k}\right)=\prod_{i=1}^{k}P\left(A_{i_k}\right).$$

• 两两独立（Pairwise independent）: 任意 $i,j=1,2,\ldots,n$, $i\ne j$, $P(A_iA_j)=P(A_i)P(A_j)$
• 思考: 相互独立与两两独立等价吗？

---

相互独立与两两独立

例： 袋中有红、白、黑球各一个，染有红、白、黑三色的彩球一个. 从袋中任取一球，记事件 $A,B,C$ 分别表示取到的球上有红、白、黑色，则

• $A,B,C$ 两两独立
  
  • $P(A)=P(B)=P(C)=\frac12$
  • $P(AB)=P(BC)=P(CA)=\frac14$
• 但 $A,B,C$ 不相互独立
  
  • $P ( A B C ) = \frac { 1 } { 4 } \neq \frac { 1 } { 8 } = P ( A ) P ( B ) P ( C )$

---

思考: 是否存在某个事件，与所有的事件相互独立？

• 必然事件（样本空间）$\Omega$ 与除了不可能事件（空事件）$\varnothing$ 之外的任意事件相互独立

---

例： 某型号速射炮单发弹击中目标的概率为 $p$，试求连续发射 $n$ 发炮弹（至少）能击中目标（一次）的概率.

• 记 $A_i=\{\text{第 i 发命中目标}\},i=1,2,...,n$
  
  • 不妨设 $A_1,A_2,...,A_n$ 相互独立.
  • $p_n=P(n\text{ 发之内命中目标})$
    
    • $= P \left( \bigcup _ { i = 1 } ^ { n } A _ { i } \right)= 1 - P \left( \bigcap _ { i = 1 } ^ { n } \overline { A } _ { i } \right)= 1 - ( 1 - p ) ^ { n }$

---

设 $p=0.001$, 则

$$p _ { n } = 1 - 0.999 ^ { n }.$$

$$\boxed{\begin{array}{c|ccccc} n & 1000 & 2000 & 3000 & 4000 & 5000 \\ \hline p_n & 0.632 & 0.865 & 0.950 & 0.982 & 0.993 \end{array}}$$

• 国产航母 1130 型近防炮[1]每分钟可发射 10000 发（每秒约 166 发）炮弹，所携炮弹可连续射击约 7.7 秒，打击飞行速度达 4 马赫来袭的空中目标，拦截成功率可达 96%

---

注：关于独立性的说明

• 即使发生的概率很小，但只要试验持续进行下去，小概率事件几乎必然要发生
  
  • 绝不能轻视小概率事件！(量变→质变)
• 关于事件独立性的确定往往需要结合问题的背景加以分析
  
  • 很多时候，对事件独立性的判断来源于常识或约定

---

系统可靠性

例：如图的电路含有四个电子元件，

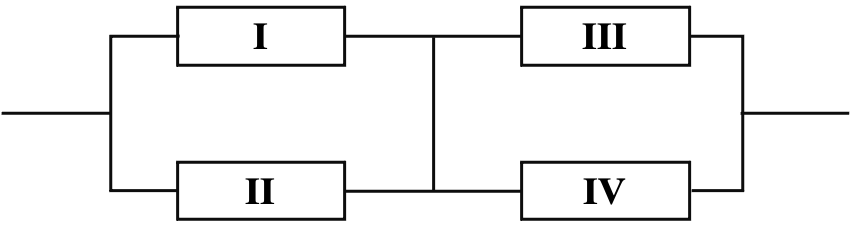
已知每个元件的个可靠性分别为 $p_i\;(i=1,2,3,4)$, 且工作中互不干扰. 求以上电路系统的可靠性.

• 系统的可靠性： 系统正常工作的概率.

---

解：

• 定义事件 $A_i=\{\text{第 i 个元件工作正常}\},\;i=1,2,3,4$.
• 系统的可靠性
  
  • $=P(A_1A_3\cup A_2A_4)$
  • $=P(A_1A_3)+P(A_2A_4)-P(A_1A_3A_2A_4)$
  • $=p_1p_3+p_2p_4-p_1p_2p_3p_4$

---

小结

• 条件概率 $P(A|B)$ 也是
  
  • 满足概率的定义，具有概率的所有性质
  • 定义的前提 $P(B)> 0$
• 事件的独立性
  
  • 与互斥的区别
  • $A,B$ 独立，则 $\overline{A}$ 与 $B$，$\overline{A}$ 与 $\overline{B}$ 独立

---

例：配对问题

某旅社共有 $𝑛$ 间客房，由于房门钥匙的编号牌丢失，只能随机地将这客房的钥匙分发给 $𝑛$ 个房间的房客，假设每个房间的钥匙都是不同的，求至少有一间房的房门可以打开的概率.

• 该问题可以视为房间钥匙的编号问题，如果某个钥匙本来的编号和分配到的编号一致（匹配），则可以打开房门.
• 令事件 $A_i$ 表示第 $i$ 间房子的钥匙和编号相匹配.
• 事件 $A$ 为至少有一个房门可以打开，$\displaystyle A=\bigcup_{i=1}^nA_i$

---

• $P(A_i)=\frac{1}{n},\;i=1,2,...,n$
• 由乘法公式
  
  • $\displaystyle P(A_iA_j)=P(A_j|A_i)P(A_i)=\frac{1}{(n-1)n}$
    
    • 其中 $1\leq i<j\leq n$
  • $\displaystyle P(A_iA_jA_k)=P(A_k|A_iA_j)P(A_j|A_i)P(A_i)=\frac{1}{(n-2)(n-1)n}$
    
    • 其中 $i\leq<i<j<k\leq n$
  • ...,
  • $\displaystyle P(A_1A_2...A_n)=\frac{1}{n!}$

---

由和事件的概率计算公式

• $\displaystyle P(A)=P\left(\bigcup_{i=1}^nA_i\right)$
  
  • $\displaystyle=\sum_iP(A_i)-\sum_{i<j}P(A_iA_j)+\sum_{i<j<k}P(A_iA_jA_k)+...+(-1)^nP(A_1A_2...A_n)$
  • $\displaystyle=C_n^1\frac{1}{n}-C_n^2\frac{1}{n(n-1)}+C_n^3\frac{1}{n(n-1)(n-2)}+C_n^n(-1)^{n-1}\frac{1}{n!}$
  • $\displaystyle=1-\frac{1}{2!}+\frac{1}{3!}+...+(-1)^{n-1}\frac{1}{n!}$

---

A mathematician is a machine for turning coffee into theorems.
-- Paul Erdös

---

课堂讨论：星期二男孩问题

• 问题一:： 一个家庭有两个孩子，其中一个是男孩. 问另一个也是男孩的概率是多少？
• 问题二： 一个家庭有两个孩子，其中一个是在周二出生的男孩. 问另一个也是男孩的概率是多少？
• 关键在于观察者掌握了多少信息. 他是只知道一个孩子的信息，还是已经观察了所有孩子、掌握了所有孩子的信息，这将决定他在做出描述时是否会在事实上删除掉一些情况，并最终影响到问题的概率.

---

课后思考：条件独立性

给定事件 $C$，如果事件 $A,B$ 满足

$$P(AB|C)=P(A|C)P(B|C),$$

则称 $A,B$ 在 $C$ 的条件下独立（条件独立）.

试研究条件独立与独立的关系.

---

The Monty Hall Problem[2]

A TV game show, Let's Make A Deal, hosted by Monty Hall.

• You are given the opportunity to select one closed door of three, behind one of which there is a prize.
• The other two doors hide “goats” (or some other such “non-prize”), or nothing at all.
• Once you have made your selection, Monty Hall will open one of the remaining doors, revealing that it does not contain the prize 2.
• He then asks you if you would like to switch your selection to the other unopened door, or stay with your original choice.
• Here is the problem: Does it matter if you switch?

---

Solution:

• When the game starts, the probability that any one of the doors contains the prize is $1/3$.
• After Monty Hall eliminated one of the doors which does not hide a prize.
  
  • If you stay with the initial choice, the probability that you win is $1/3$.
  • If you switch to the left one, the probability that you win is $2/3$.
• Why?