@blueband21c
2023-04-24T12:47:17.000000Z
字数 10339
阅读 4268
第十七讲 期望、协方差与相关系数
概率论与数理统计 讲义 NUDT 2023SP
17.1 随机向量的函数的期望
已知 rv 的 pmf 或 pdf ,函数 的期望为
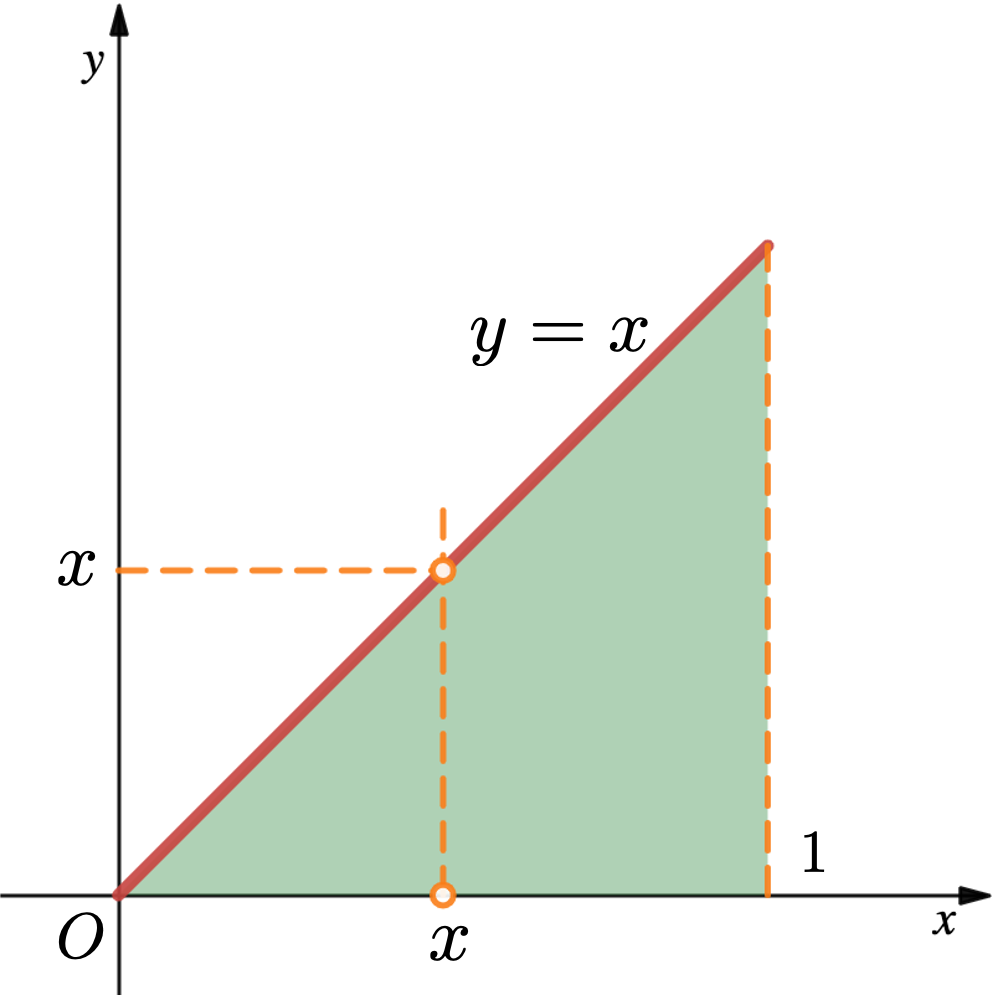
例: 设 rv 的 pdf 为
求 .
解:
数学期望的线性性
定理:若 rv 的期望都存在,则
- 推论: 设 rv 都有有限的期望值,则对任意
例:二项随机变量的数学期望
设 ,求 .
- 记 ,则 .
期望与随机变量的独立性
定理:若 rv 相互独立且期望均存在,则
- 注:由 无法推出 相互独立.
例:单位圆盘上的均匀分布
设 rv 服从 上的均匀分布, 验证
- 不相互独立
验证
验证 不相互独立
17.2 协方差
若 rv 的方差都存在,则
-
- 定义 为 的协方差( covariance )
- 记号:
协方差的性质
- 思考: 设 , 则
协方差与随机变量的独立性
定理:若 rv 相互独立且方差均存在,则
协方差的意义
- 若 , 则 不相互独立.
- 不相互独立,意味着 的取值存在某种联系
- 问题:可否/如何度量这种联系的“强度”?
- 例: 任取 , 则
- 如果使用协方差来度量两个随机变量之间的联系,则上式意味着 之间的联系比 之间的更强!
- 由此可见,直接使用协方差来度量两个随机变量之间联系的强度并不完全合适
相关系数
随机变量 的相关系数 (correlation coefficient) 定义为
- 其他记号:,,
- 若令
- 则
- 称为 的 标准化随机变量(standardized rv).
相关系数的性质
- 对任意的 rv , .
- 若 相互独立,则
- 但是, 无法推出 相互独立
- 对任意 ,若
- 则
- ,当且仅当存在 ,使得 几乎处处(almost everywhere, 缩写:a.e.)成立
随机变量的线性相关性
问题:如果用 rv 的线性函数 近似 rv ,最好的情况下可以近似到什么程度?
- 以均方方差(mean square error) 作为评价的标准
- 越小,则近似程度越高
- 如果存在某一对 ,使得 ,则意味着 是几乎处处成立的
最佳线性近似的求解
- 可以视为 的函数,为了使其最小,令 .
- 也即
- 解得 .
- 由上式可知,当且仅当 时, 的最小值为 .
相关性的意义
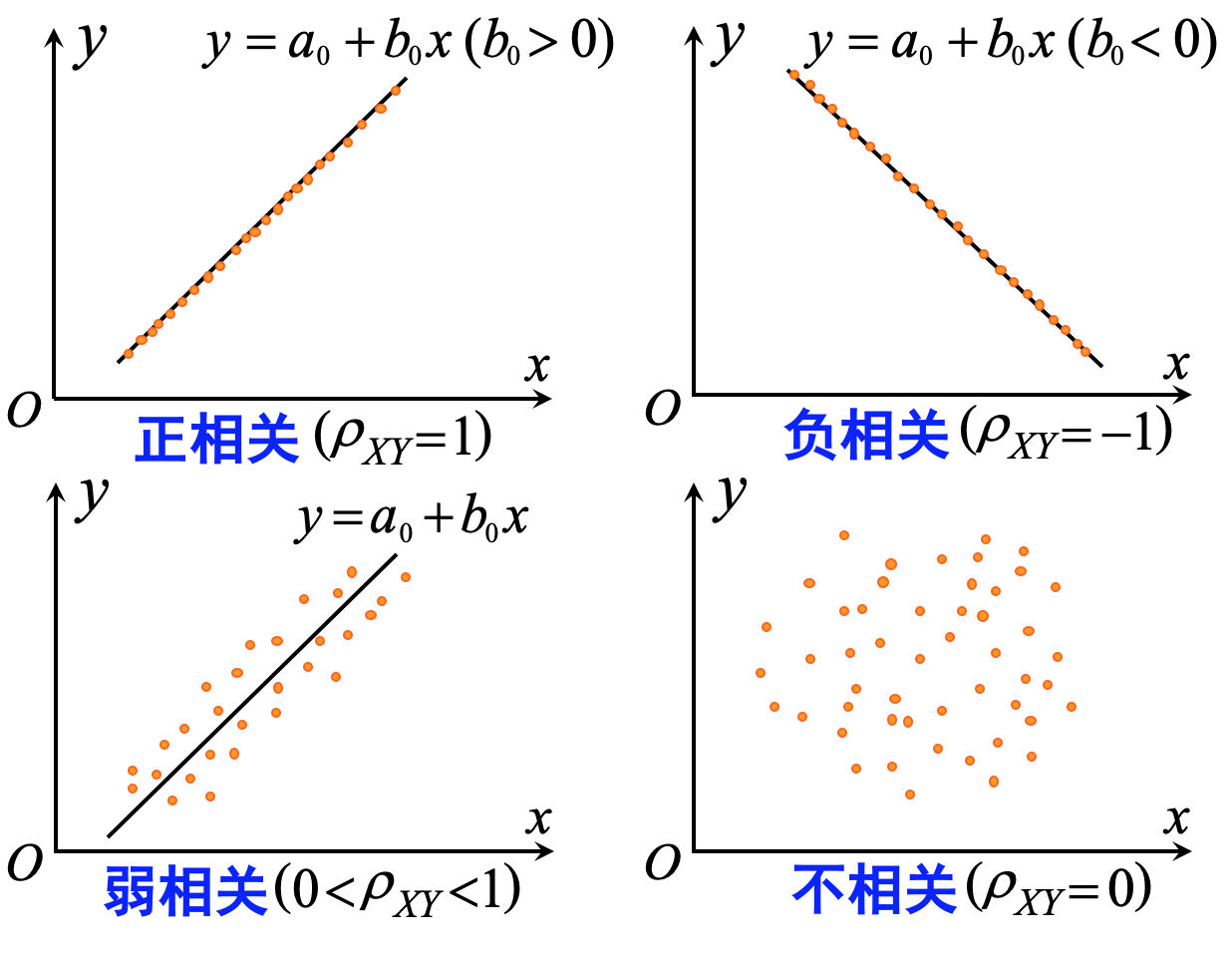
- 相关系数刻画了两个随机变量之间线性关系的强弱
- 两个随机变量相互独立,则取值之间不存在任何联系或依赖关系
- 两个随机变量的取值不存在线性关系,并不一定能说明它们之间不存在其他类型的依赖关系
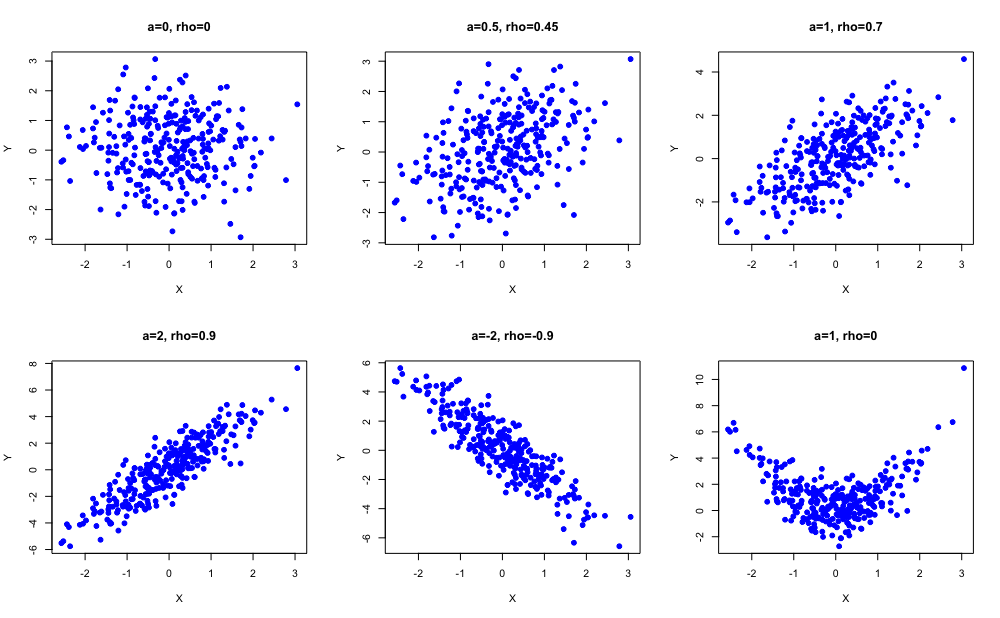
例:从线性模型到非线性模型
考虑线性模型: , 其中 , 相互独立. 求 ?
- 讨论: 如果改为二次模型:, 会有怎样的变化?
17.3 二维正态分布
设 相互独立且均服从 ,则其联合密度函数为
- 记 , 则可记
- 随机向量 的分布称为 二维标准正态分布(two dimensional standard normal distribution)
一般的二维正态分布
设 相互独立且均服从 ,令
其中 且 .
- 随机向量 的分布称为二维正态分布
记
- 则 .
- 若 , 则 .
- .
- 于是 的联合密度函数
- 记为:
注记
- 若 , 则 是正定矩阵
- 此时,可记 .
- 由 , 可知
- 由此可知二维正态分布可由五个相互独立的参数确定:
- 因此二维正态分布也记为
二维正态分布的密度函数
二维正态分布的性质
若 ,则
-
- 相互独立当且仅当
- 正态随机变量的独立与不相关相互等价
- ,则 仍服从正态分布
- 正态分布的线性组合仍为正态分布
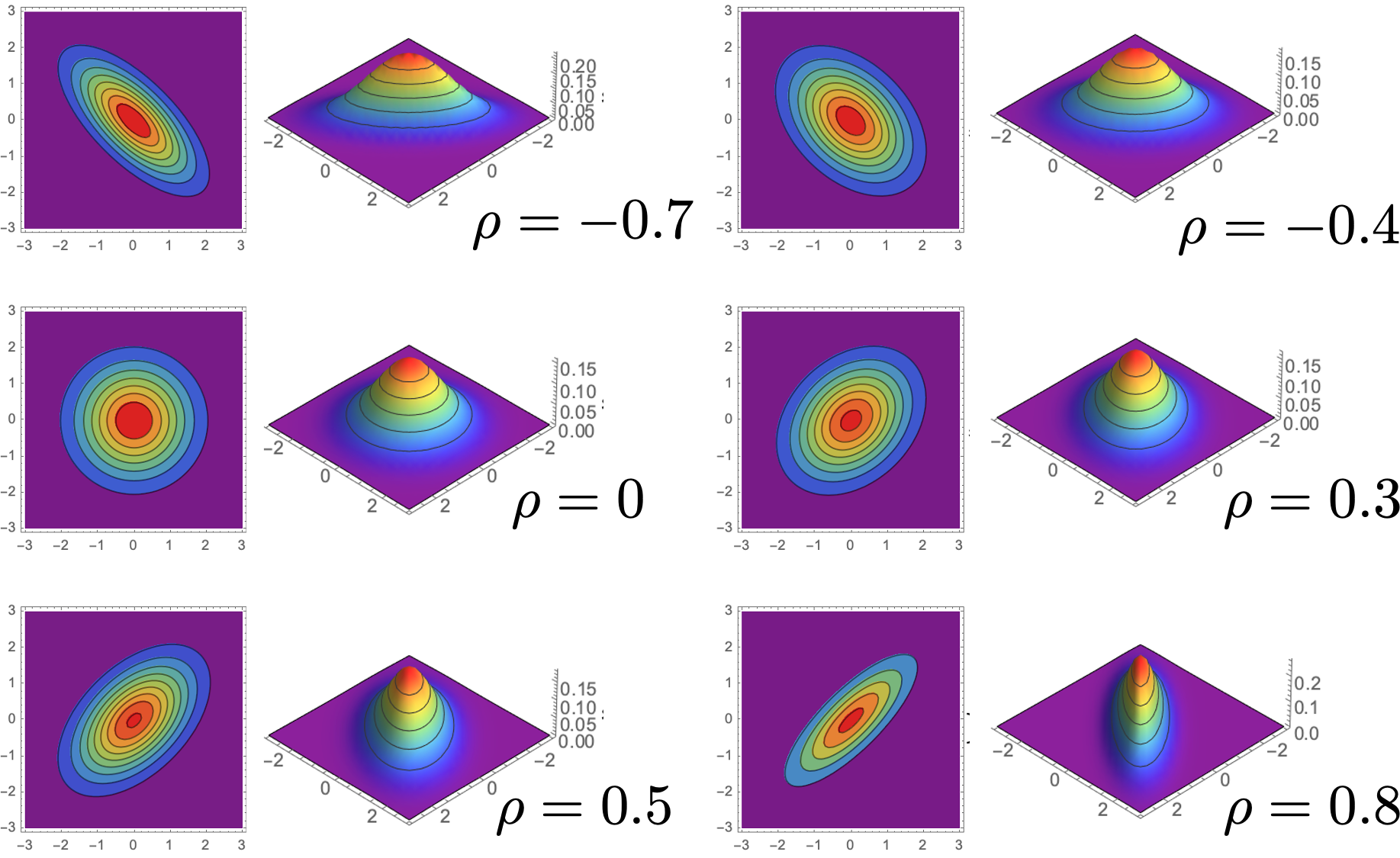
不同相关系数下对应的二维正态分布的形态.
n 维正态分布
设 相互独立均服从 , 令
其中矩阵 行满秩,, 则随机向量 的分布称为 n 维正态分布
记
因为 行满秩,故 , 于是 的联合密度
- 记为: .
多个正态随机变量的独立性
定理:若 , 则
- 相互独立,当且仅当 为对角阵.
协方差阵
对 维随机向量 , 称为其对应的 协方差阵(covariance matrix)
- 若记 ,协方差阵通常也记为 或
- 定理: 记 ,则
小结
- 熟练掌握期望和协方差的性质与计算公式
- 理解相关性的含义
- 熟练掌握相关系数的计算公式:
- 理解二维正态分布的性质和参数的含义
- 正态随机变量的线性组合仍为正态随机变量
- 正态随机变量的相互独立与不相关等价
Science is a way of thinking much more than it is a body of knowledge.”
--Carl Sagan
