第十二讲 混合型随机变量

概率论与数理统计 讲义 NUDT 2023SP

---

---

复习回顾：常用的随机分布

$$\begin{array}{cccccl} %\hline \text{随机分布} & \text{符号} & \text{分布律/密度函数} & \text{期望} & \text{方差} & \text{应用背景}\\ \hline \text{“0-1”分布} & b(1,\alpha) & \begin{pmatrix} 1 & 0 \\ \alpha & 1-\alpha \end{pmatrix} & \alpha & \alpha(1-\alpha) & \text{Bernoulli 试验}\\[1ex] %\hline \text{二项分布} & b(n,\alpha) & \begin{array}{c}p(x)=C_n^x\alpha^x(1-\alpha)^{n-x},\\ x=0,1,...,n\end{array} & n\alpha & n\alpha(1-\alpha) & \text{二项试验 (}n\text{ 重 Bernoulli 试验)}\\ %\hline \text{Poisson分布} & P(\mu) & \displaystyle p(x)=\mathrm{e}^{-\mu}\frac{\mu^x}{x!},\;x=0,1,... & \mu & \mu & \begin{array}{l}\text{Poisson 流中一定时间内}\\ \text{特定事件发生的次数}\end{array}\\ %\hline \text{均匀分布} & U(A,B) & \displaystyle f(x)=\frac{1}{B-A}I_{[A,B]}(x) & \displaystyle \frac{A+B}{2} & \displaystyle \frac{(B-A)^2}{12} & \text{直线上的等可能概型}\\[1ex] %\hline \text{正态分布} & N(\mu,\sigma^2) & f(x)=\displaystyle\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) & \mu & \sigma^2 & \text{随机误差的分布}\\ %\hline \text{指数分布} & \mathrm{Exp}(\lambda) & f(x)=\lambda\exp\left(-\lambda x\right)I_{[0,\infty)}(x) & \displaystyle \frac{1}{\lambda} & \displaystyle \frac{1}{\lambda^2} & \text{“寿命”的分布} \end{array}$$

---

12.1 奇异连续分布

满足以下两个条件的分布函数称为奇异连续分布（singular continuous distribution）:

1. 分布函数是连续的；

2. 分布函数导数非零的点非常少（Lebesgue 测度为 $0$）

   • 注： Lebesgue 测度为 $0$ 可以理解为集合的“长度”为 $0$，例如：任意可数集的“长度”都是 $0$.

---

Cantor 集

Cantor 集是一个非可列但测度为 $0$ 的集合.

$$C=\bigcap_{n=1}^{\infty}\bigcup_{k=0}^{3^{n-1}-1}\left(\left[\frac{3k+0}{3^n},\frac{3k+1}{3^n}\right]\cup\left[\frac{3k+2}{3^n},\frac{3k+3}{3^n}\right] \right)$$

---

Cantor 分布函数

---

分布函数的 Lebesgues 分解

定理：任意一个分布函数 $F$ 都可以分解为如下形式

$$F(x)=c_1F_1(x)+c_2F_2(x)+c_3F_3(x),$$

其中 $F_1,F_2,F_3$ 分别为连续分布函数、离散分布函数和奇异连续分布函数，且满足

$$c_1+c_2+c_3=1,\;c_1,c_2,c_3\geq 0.$$

• 该定理说明，分布函数有且仅有三种基本类型（离散、连续、奇异连续），且任一分布函数都可以表示为三种基本类型的凸组合形式.

---

12.2 混合型随机变量

设 $F_1(x),F_2(x)$ 分别为离散型随机变量 $X_1$ 和连续型随机变量 $X_2$ 的分布函数. 给定 $c_1,c_2>0$ 满足 $c_1+c_2=1$, 则

$${F(x)=c_1F_1(x)+c_2F_2(x)}$$

可以视为某个随机变量的分布函数.

• 若随机变量 $X$ 以以上的 $F(x)$ 为分布函数, 则称其为一个 混合型随机变量 (rv with mixed distribution).[1]

---

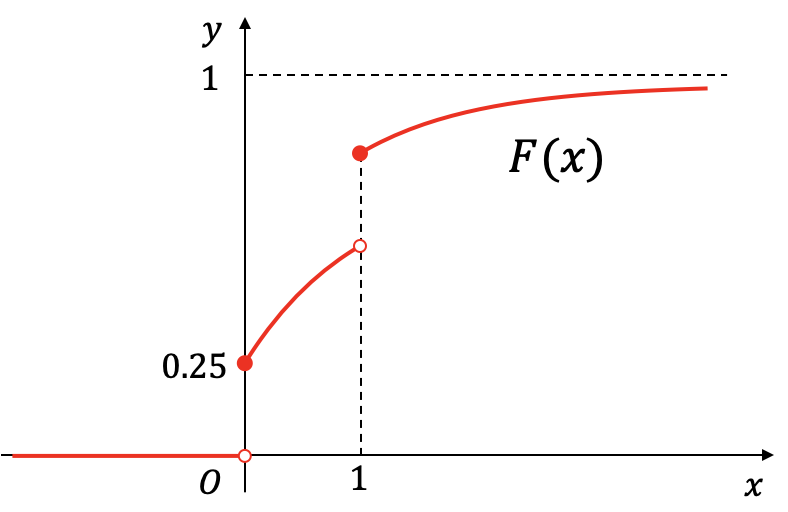
例：验证随机变量是混合型的

设随机变量 $X$ 的分布函数为

$$F(x)=\left\{\begin{array}{cc} {0,} & {x<0} \\ \frac{1}{2}\left(1-\mathrm{e}^{-x}\right)+\frac{1}{4}, &0 \leq x<1\\ {\frac{1}{2}\left(1-\mathrm{e}^{-x}\right)+\frac{1}{2},} & {x \geq 1}\end{array}\right.$$

验证 $X$ 是一个混合型随机变量.

---

观察分布函数的图像

---

分布函数的分解

$${F}(x)=\widetilde{F}_1(x)+\widetilde{F}_2(x)$$

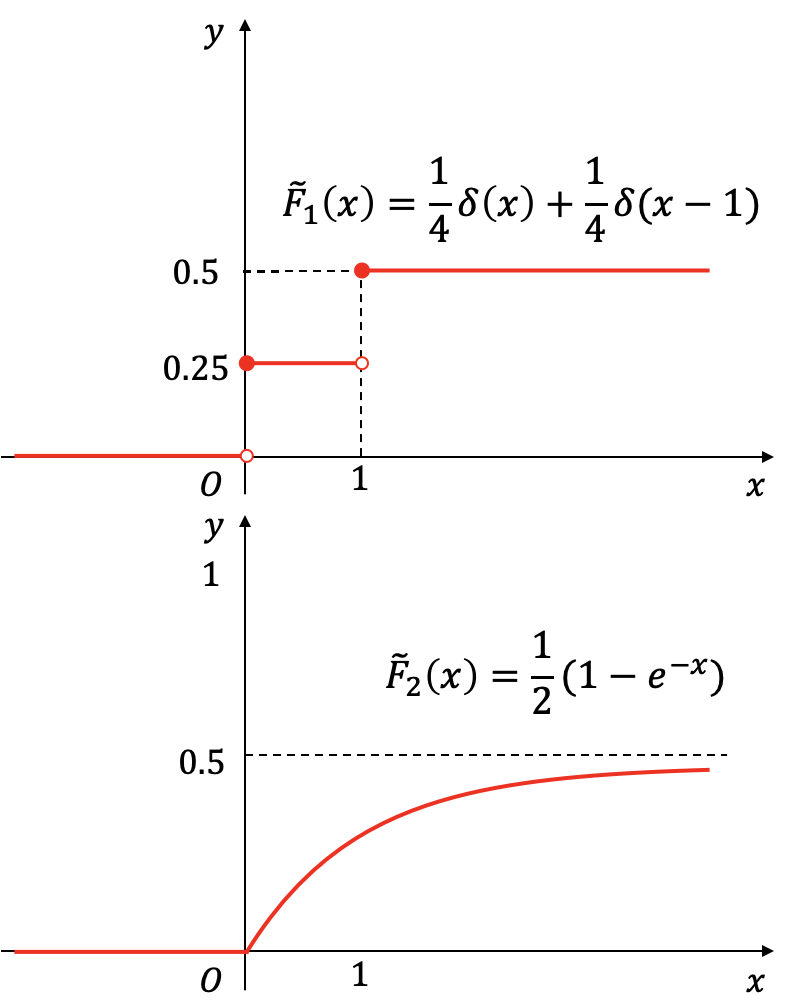
• 注意： 以上的 $\widetilde{F}_1(x)$ 和 $\widetilde{F}_2(x)$ 都不是一个“合法”的分布函数！
  
  • 因为不满足：$F(+\infty)=1$.

---

分析： 为了将 $\widetilde{F}_1(x)$ 和 $\widetilde{F}_2(x)$ 转换为合法的分布函数，需要对它们分别进行规范化（normalize），定义

$$\begin{array}{l}{F_{1}(x)=\frac{\widetilde{F}_{1}(x)}{\widetilde{F}_{1}(+\infty)} =\frac{1}{2} \delta(x)+\frac{1}{2} \delta(x-1)} \\ {F_{2}(x)=\frac{\widetilde{F}_{2}(x)}{\widetilde{F}_{2}(+\infty)} =1-\mathrm{e}^{-x}(x \geq 0)}\end{array}$$

• 于是 $F(x)=\frac{1}{2} F_{1}(x)+\frac{1}{2} F_{2}(x)$.
• 由此可知 $X$ 是由 $X_1\sim b(1,0.5)$ 和 $X_2\sim\mathrm{Exp}(1)$ 的分布函数加权组合而成的混合型随机变量.

---

课堂练习

• 设随机变量 $X$ 的绝对值不大于 $1$，且 $\displaystyle P\{X=-1\}=\frac{1}{8}$，$\displaystyle P\{X=1\}=\frac{1}{4}$.
• 在事件 $\{-1 < X < 1\}$ 发生的前提下，$X$ 在 $(-1,1)$ 的任一子区间上取值的概率与该子区间的长度成正比.
• 求 $X$ 的分布函数.
• 验证该随机变量是一个混合型随机变量.

---

分析：

• $P\{-1 < X < 1\}=1-P\{X=1\}-P\{X=-1\}=\frac{5}{8}.$
• 由已知，设 $P\{-1 < X< x|-1 < X < 1\}=k(x+1)$, 其中 $k$ 为常数.
• 注意到 $P\{-1 < X< 1|-1 < X < 1\}=1$，故 $k=\frac{1}{2}$.
• 因为 $X$ 的取值不可能小于 $-1$，故当 $x<-1$ 时，$F(x)=0$.
• 因为 $X$ 的取值不可能大于 $1$，故当 $x\geq 1$ 时，$F(x)=1$.

---

• 当 $-1\leq x<1$ 时,
  
  • $F(x)=P\{X\leq x\}=P\{X\leq -1\}+P\{-1 < X\leq x\}$
    
    • $\displaystyle =\frac{1}{8}+P\{-1 < X\leq x|-1 < X < 1\}P\{-1 < X < 1\}$
    • $\displaystyle =\frac{1}{8}+\frac{5}{8}\cdot\frac{x+1}{2}=\frac{5x+7}{16}.$
• 综上，$F(x)=\left\{\begin{array}{cc} 0 & x < -1,\\ \displaystyle\frac{5x+7}{16} & -1\leq x < 1\\ 1 & 1\leq x. \end{array}\right.$

---

• 验证：
  
  • $\displaystyle F(x)=\frac{3}{8}F_1(x)+\frac{5}{8}F_2(x)$
  • $\displaystyle F_1(x)=\frac{1}{3}\delta(x+1)+\frac{2}{3}\delta(x-1)$
  • $F_2(x)=\left\{\begin{array}{cc} 0 & x < -1,\\ \displaystyle\frac{x+1}{2} & -1\leq x < 1\\ 1 & 1\leq x. \end{array}\right.$

---

重要的说明

• 本门课程中所说的混合型随机变量，严格来说，应该叫做具有混合型分布函数的随机变量.
• 事实上，如果 $X_1,X_2$ 分别以 $F_1,F_2$ 为分布函数，$X_3$ 以 $c_1F_1+c_2F_2$ 为分布函数，并不能推出 $X_3=c_1X_1+c_2X_2$.
• 换言之，分布函数的组合不能等同于随机变量的组合.

---

两个连续型随机分布的组合

设连续型随机变量 $X_1,X_2$ 的密度和分布函数分别为 $f_1,f_2$ 和 $F_1,F_2$，且随机变量 $X$ 的分布函数为

$$F(x)=\alpha F_1(x)+(1-\alpha)F_2(x).$$

• 由此易得 $X$ 的密度函数 $f(x)=\alpha f_1(x)+(1-\alpha)f_2(x)$.
• 问题：由以上的关系可以推出 $X=\alpha X_1+(1-\alpha)X_2$ 吗？

---

分析： 记 $Y=\alpha X_1+(1-\alpha)X_2$.

• 容易验证 $E(Y)=\alpha E(X_1)+(1-\alpha)E(X_2)=E(X).$
• $E(Y^2)=\bbox[yellow]{\alpha^2E(X_1^2)+(1-\alpha)^2E(X_2^2)+2\alpha(1-\alpha)E(X_1X_2)}$
• $E(X^2)=\alpha\int_{\mathbb{R}}x^2f_1(x)\mathrm{d}x+(1-\alpha)\int_{\mathbb{R}}x^2f_2(x)\mathrm{d}x$
  
  • $=\bbox[lightgreen]{\alpha E(X_1^2)+(1-\alpha)E(X_2^2).}$
• 如果两个随机变量的某个数字特征不同，则必不是相同的随机变量.

---

例：排队系统

• 在某个排队系统中，记客户到达后需要等待的时间为随机变量 $X$.
• 如果前面没有其他客户，则 $X=0$.
• 如果已经有其他客户在排队，则 $X\sim\mathrm{Exp}(\lambda)$.
• 已知前方有其他客户在排队的概率为 $p$.
• 试求 $X$ 的分布函数.

---

解： 定义事件 $A$ 表示前面有其他客户在排队.

$$\begin{aligned} F(x) &=P\{X \leq x\} \\ &=P\{X \leq x | \overline{A}\} P(\overline{A})+P\{X \leq x | A\} P(A) \\ &=\left\{\begin{array}{cc}0,& x<0 \\ 1 \cdot p+(1-p)\left(1-\mathrm{e}^{-\lambda x}\right), &x \geq 0\end{array}\right.\\ &=p \delta(x)+(1-p) {F}_1(x) \end{aligned}$$

其中

$$\delta(x)=\left\{\begin{array}{ll}{0,} & {x<0} \\ {1,} & {x \geq 0}\end{array}\right. \quad {F}_1(x)=\left\{\begin{array}{cc}{0,} & {x<0} \\ {1-\mathrm{e}^{-\lambda x},} & {x \geq 0}\end{array}\right.$$

---

随机变量的组合与分布函数的组合

定理： 设随机变量 $X,X_1,X_2$ 的分布函数分别为 $F_X,F_1,F_2$，随机变量 $B\sim b(1,\alpha)\;(\alpha\in(0,1))$ 与 $X_1,X_2$ 相互独立，且

$$X=B X_1+(1-B)X_2.$$

则

$$F_X(x)=\alpha F_1(x)+(1-\alpha) F_2(x).$$

• 注： 随机变量 $X,Y$ 相互独立，当且仅当对任意 $x,y\in\mathbb{R}$，$\{X\leq x\}$ 与 $\{Y\leq y\}$ 相互独立.

---

提示：

• $F_X(x)=P\{X\leq x\}$
  
  • $=P\{X\leq x|B=1\}P\{B=1\}+P\{X\leq x|B=0\}P\{B=0\}$
  • $=\alpha P\{X_1\leq x\}+(1-\alpha)P\{X_2\leq x\}$
  • $=\alpha F_1(x)+(1-\alpha)F_2(x)$

---

小结

• 理解混合型随机变量的概念
• 掌握混合型随机变量的 cdf 的计算方法

---

Logic and mathematics are nothing but specialised linguistic structures.
-- Jean Piaget

---

补充例题

设随机变量 $X,Y$ 相互独立，$X$ 的概率分布为

$$P\{X=x\}=\frac{1}{3},\quad x=-1,0,1.$$

随机变量 $Y$ 的密度函数为 $f_Y(y)= \left\{\begin{array}{cc} 1 & 0\leq y < 1 \\ 0 & \text{其他} \end{array}\right.$. 记 $Z=X+Y$.

(1) 求 $\displaystyle P\left\{Z\leq\frac{1}{2}\bigg|X=0\right\}$. (2) 求 $Z$ 的概率密度 $f_Z(z)$.

---

解：(1) 因为随机变量 $X,Y$ 相互独立，

$$\begin{aligned} P&\left\{Z\leq\frac{1}{2}\bigg|X=0\right\}=P\left\{X+Y\leq\frac{1}{2}\bigg|X=0\right\}\\ &=P\left\{Y\leq\frac{1}{2}\bigg|X=0\right\}=P\left\{Y\leq\frac{1}{2}\right\}\\ &= \int_{-\infty}^{1/2} f_Y(y) \mathrm{d} y=\int_0^{1/2}1\mathrm{d}y=\frac{1}{2}. \end{aligned}$$

(2) $Y$ 的分布函数 $F_Y(y)= \left\{\begin{array}{cc} 0 & y<0 \\ y & 0\leq y <1\\ 1 & \text{其他} \end{array}\right.$

---

$$\begin{aligned} F_Z(z)&=P\{Z\leq z\}=P\{X+Y\leq z\}\\ &=P\{X+Y\leq z|X=-1\}P\{X=-1\}+P\{X+Y\leq z|X=0\}P\{X=0\}\\ &\quad +P\{X+Y\leq z|X=1\}P\{X=1\}\\ &=\frac{1}{3}\left[F_Y(z+1)+F_Y(z)+F_Y(z-1)\right]\\ &= \left\{\begin{array}{cc} 0 & z\leq -1 \\ \frac{z+1}{3} & -1\leq z<2 \\ 1 & \text{其他} \end{array}\right. \end{aligned}$$

于是 $f_Z(z)=\displaystyle \frac{\mathrm{d}}{\mathrm{d}z}F_Z(z)= \left\{\begin{array}{cc} \frac{1}{3} & -1\leq z<2 \\ 0 & \text{其他} \end{array}\right.$