第二十八讲 课程小结

概率论与数理统计 讲义 NUDT 2023SP

---

---

1. 事件与概率

• 和事件的概率
  
  • $\bbox[yellow]{P(A\cup B)=P(A)+P(B)-P(AB)}$
  • $P(A\cup B\cup C)=\underline{\hspace{20cm}}$
  • $P\left( \bigcup_{i=1}^n A_i \right)=\underline{\hspace{20cm}}$

---

• 乘法公式
  
  • $P(AB)=P(A|B)P(B)$
  • $P(ABC)=P(A|BC)\underline{\hspace{10cm}}P(C)$
• $A,B$ 相互独立时
  
  • $P(A|B)=P(A)$ $P(AB)=P(A)P(B)$
  • $A$ 与 $\overline{B}$，$\overline{A}$ 与 $B$，$\overline{A}$ 与 $\overline{B}$ 均相互独立

---

• 几个概念问题
  
  • 两事件独立与互斥的关系？
  • 多个事件相互独立与两两独立的关系？
  • 事件两两互斥与相互排斥的关系？
  • 定义条件概率 $P(A|B)$ 有什么前提条件？

---

• 全概率公式：$\bbox[yellow]{P(B)=\sum\limits_{i=1}^nP(BA_i)=\sum\limits_{i=1}^nP(B|A_i)P(A_i)}$
  
  • 其中 $A_i\;(i=1,...,n)$ 满足 $\underline{\hspace{10cm}}$
• Bayes 公式：$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$
  
  • 或 $\underline{\hspace{5cm}}=\frac{{\hspace{10cm}}}{\sum\limits_{i=1}^nP(B|A_i)P(A_i)},\;j=1,2,...,n.$

---

2. 古典概型

• 古典概型：1）有限个可能的结果；2）所有结果等可能出现.
• $P(A)=\frac{N(A)}{N(\Omega)}$
• 典型问题：摸球问题 (区分有无放回)、生日问题
• 计数方法：排列、组合，注意计数方法的一致性，避免漏计和重复计数

---

3. 随机变量

• 离散型：可数多个可能的取值
• 连续型：$P\{X\in I\}=\int_If(x)\mathrm{d}x$
  
  • 对任意 $a\in\mathbb{R}$，$P\{X=a\}=0$.
• 混合型：$X$ 的分布函数 $F(x)=cF_1(x)+(1-c)F_2(x)$, $c\in(0,1)$
  
  • 其中 $X_1\sim F_1(x)$，$X_2\sim F_2(x)$ 分别为离散和连续型随机变量
  • 注意：由前式不能推出 $X=cX_1+(1-c)X_2$

---

离散型随机变量

• 分布律：$p(x)=\underline{\hspace{10cm}}$
• 分布函数：$F(x)=P\{X\leq x\}=\underline{\hspace{5cm}p(\qquad)}$
  
  • $p(x)=\underline{F(x)-F(x-0)}$
• 期望：$\bbox[yellow]{E(X)=\underline{\hspace{10cm}}}$
• 方差：$\bbox[yellow]{D(X)=E(\underline{\hspace{10cm}})}$
  
  • $\bbox[yellow]{D(X)=E(X^2)-[E(X)]^2}$

---

连续型随机变量

• 密度函数：$f(x)=\frac{\mathrm{d}}{\mathrm{d}x}F(x)$
• 分布函数：$F(x)=P\{X\leq x\}=\int_{-\infty}^xf(t)\mathrm{d}t$
  
  • 要求密度函数，先求分布函数!
• 期望：$\bbox[yellow]{E(X)=\underline{\hspace{10cm}}}$
• 方差：$\bbox[yellow]{D(X)=\int_{\underline{\;}}^{\underline{\;}}\underline{\hspace{8cm}}}=E(X^2)-[E(X)]^2$

---

常用的随机变量及其分布

• 熟练掌握
  
  • Bernoulli (“0-1”) 分布
  • 二项分布
  • Poisson 分布
  • 均匀分布
  • 正态分布
  • 指数分布
• 了解
  
  • 几何分布
  • 超几何分布
  • 负二项分布
  • Gamma 分布
  • 对数正态分布

---

常用的随机变量及其分布

---

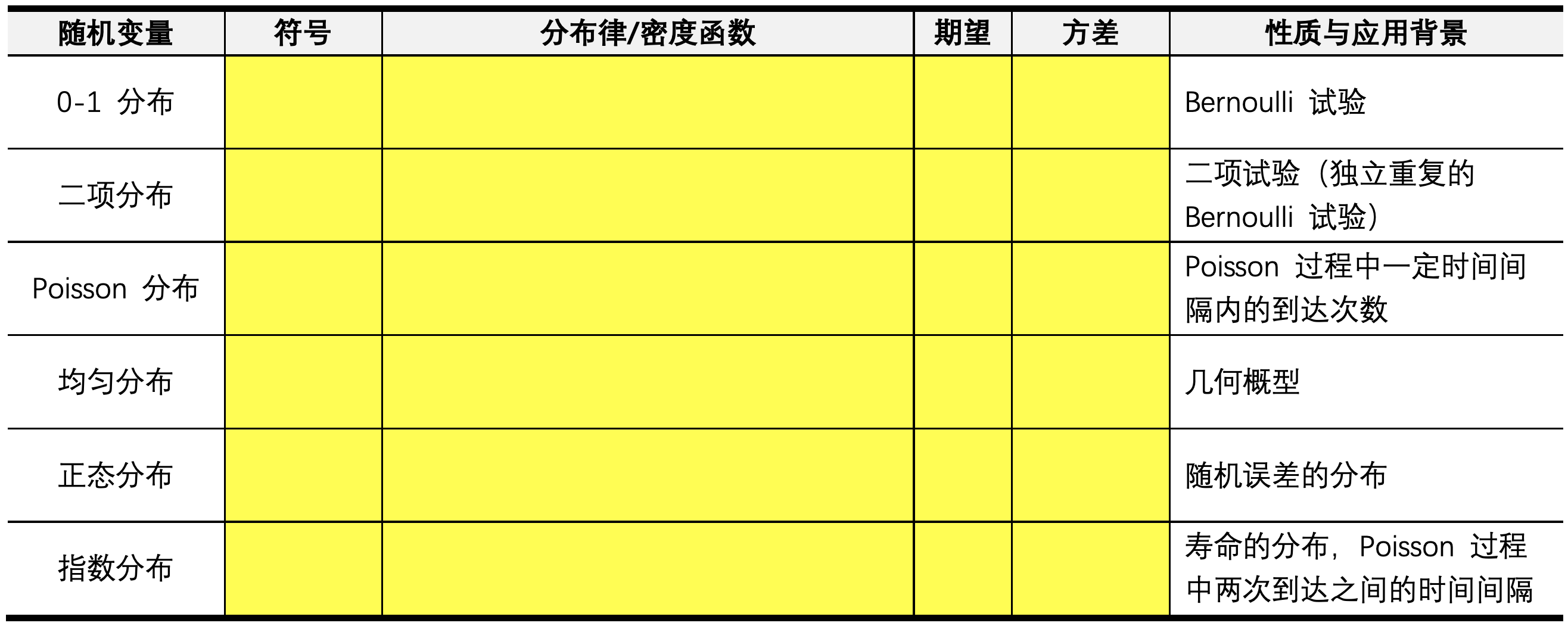
随机变量的应用背景

• 在 Poisson 流中，
  
  • Poisson 随机变量刻画了一定时间间隔内特定事件发生的次数（Poisson 强度 $\alpha$ 对应于单位时间内平均的发生次数，时间间隔 $t$ 内的发生次数 $\bbox[yellow]{T\sim\underline{\hspace{6cm}}}$.）
  • 指数分布刻画了相邻两次事件发生的时间间隔
• 指数分布：寿命的分布（前提：不考虑自然老化的影响）
  
  • $\mathrm{Exp}(\lambda)$ 中：$\lambda$ 的含义是 $\underline{\hspace{5cm}}$
  • $\mathrm{EXP}(\mu)$ 中：$\mu$ 的含义是 $\underline{\hspace{5cm}}$

---

正态分布

• 正态随机变量的线性变换仍然为正态随机变量
  
  • $X\sim N(\mu,\sigma^2)$，则 $\frac{X-\mu}{\sigma}\sim N(0,1)$.
• 相互独立的正态随机变量的线性组合仍然服从正态分布
  
  • $X_i\sim N(\mu_i,\sigma_i^2),a_i\in\mathbb{R},i=0,1,2,...,n$，则 $\bbox[yellow]{a_0+\sum\limits_{i=1}^na_iX_i\sim \underline{\hspace{8cm}}}$
  • $X_1,X_2,...,X_n$ 独立同分布 $N(\mu,\sigma^2)$，则 $\bbox[yellow]{\overline{X}\sim \underline{\hspace{8cm}}}$

---

正态分布的分位点与分布函数

• 分布函数与分位点互为反函数
• $u_{\alpha}=-u_{1-\alpha}$
• $\bbox[yellow]{\Phi(x)+\Phi(-x)=\underline{\hspace{5cm}}}$
• $X\sim N(\mu,\sigma^2)$，则 $\bbox[yellow]{P\{a\leq X\leq b\}=\Phi(\underline{\hspace{5cm}})-\Phi(\underline{\hspace{5cm}})}$

---

4.多维随机变量（随机向量）

• 关键词
  
  • 联合 vs 边缘 vs 条件
  • 期望，方差
  • 协方差
  • 相关系数

---

联合与边缘的关系

---

条件分布

• 离散型的条件分布律 $p_{X|Y}(x|y)=\frac{p(x,y)}{p_Y(y)},\;\bbox[yellow]{(p_Y(y)\ne 0)}$
• 连续型的条件密度函数 $f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)},\;\bbox[yellow]{(f_Y(y)\ne 0)}$
• 要点
  
  • 计算 $f_X(x)$ 时，先讨论 $x$ 的取值范围，确定有效积分区间
  • 写 $f_{X|Y}(x|y)$ 时，必须在 $f_Y(y)\ne 0$ 的范围内

---

随机变量的独立性

• $X,Y$ 相互独立，等价于由它们分别定义的所有事件相互独立
  
  • $p(x,y)=p_X(x)p_Y(y)$
  • $f(x,y)=f_X(x)f_Y(y)$
  • $F(x,y)=F_X(x)F_Y(y)$
• 使用可分离变量的条件判定独立性时，要仔细检查联合分布中 $x,y$ 的取值范围是否可分离

---

随机变量函数分布

• 离散型随机变量：$Y=g(X)$

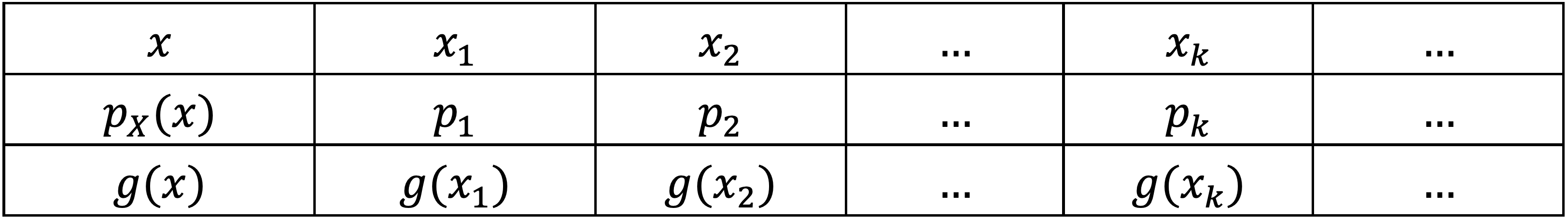
• 确定 $Y$ 的取值范围, 然后合并取值相同的项对应的概率.

---

• 连续式随机变量: $Y=g(X)$，其中 $g$ 单调可微，有反函数 $h$，
  
  • 则 $\bbox[yellow]{f_{Y}(y)=\left\{\begin{array}{cc}{{\underline{\hspace{10cm}}}} & {h(y)}\in D \\ {0,} & {\text {其他}}\end{array}\right.}$
  • $\bbox[yellow]{\text{当 }g(x)\text{ 非单调时，分成多个单调区间使用公式}}$
• 连续型随机向量: $\left\{\begin{array}{l}U=g_1(X,Y)\\ V=g_2(X,Y)\end{array}\right.$，其中 $g_1,g_2$ 可微 且有逆变换 $h_1,h_2$
  
  • 则 $\bbox[yellow]{f_{U V}(u, v)=\left\{\begin{array}{cc}{\underline{\hspace{10cm}}} & {(u, v)\text{取值有效}} \\ {0} & {\text {其他}}\end{array}\right.}$

---

和(差)的分布：卷积公式

• $\bbox[yellow]{f_{X\pm Y}(u)=\int_{-\infty}^{\infty}f(\underline{\qquad}, \underline{\qquad}) \mathrm{d} v}$
• 离散型的卷积公式：$p_{X\pm Y}(u)=\underline{\hspace{10cm}}$
• 和的分布保持分布类型不变的随机变量：正态、二项、Poisson

---

最值的分布

• 设 $X_1,X_2,...,X_n$ 独立同分布
  
  • $X_{(n)}=\max\{X_1,X_2,\ldots,X_n\}$
    
    • cdf: $\bbox[yellow]{F_{\max}(z)=\underline{\hspace{10cm}}}$
    • pdf: $\bbox[yellow]{f_{\max}(z)=\underline{\hspace{10cm}}}$
  • $X_{(1)}=\min\{X_1,X_2,\ldots,X_n\}$
    
    • cdf: $\bbox[yellow]{F_{\min}(z)=\underline{\hspace{10cm}}}$
    • pdf: $\bbox[yellow]{f_{\min}(z)=\underline{\hspace{10cm}}}$
• 掌握以上公式的推导方法!

---

5. 期望、方差、协方差与相关系数

已知 $(X,Y)$ 的 pdf $f(x,y)$，则

• $\bbox[yellow]{E(g(X,Y))=\underline{\hspace{10cm}}}$
• $E(X)=\iint_{\mathbb{R}^2}xf(x,y)\mathrm{d}x\mathrm{d}y$
• $E(g(X))=\int_{-\infty}^{+\infty}g(x)f_X(x)\mathrm{d}x=\iint_{\mathbb{R}^2}\underline{\hspace{10cm}}\mathrm{d}x\mathrm{d}y$

---

• $\bbox[yellow]{D(X+Y)=\underline{\hspace{10cm}}}$
  
  • 若 $X,Y$ 不相关，则 $D(X+Y)=D(X)+D(Y)$
• $\bbox[yellow]{\mathrm{Cov}(X,Y)=\underline{\hspace{10cm}}}$
  
  • $\bbox[yellow]{=E(XY)-E(X)E(Y)}$
• $\bbox[yellow]{\rho_{X,Y}=\underline{\hspace{10cm}}}$

---

常用的性质

• $E(aX+bY)=aE(X)+bE(Y)$
• $E(c)=c$
• $\bbox[yellow]{D(aX+b)=a^2D(X)}$
• $D(c)=0$
• $\bbox[yellow]{\mathrm{Cov}(c,Y)=0}$
• $\mathrm{Cov}(aX+bY,Z)=a\mathrm{Cov}(X,Z)+b\mathrm{Cov}(Y,Z)$

---

独立性与相关性

• 独立必不相关，反之不然
• $|\rho_{X,Y}|\leq 1$
• $|\rho_{X,Y}|=1$ 意味着 $Y=aX+b$ 几乎处处成立
• 正态随机变量相互独立等价于不相关

---

二维正态分布

$\bbox[yellow]{(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)}$

• 当且仅当
  
  • $X\sim N(\mu_1,\sigma_1^2)$
  • $Y\sim N(\mu_2,\sigma_2^2)$
  • $\rho_{X,Y}=\rho$

---

6. 大数定律与中心极限定理

• Khinchin 大数定理： $\{X_n\}$ 独立同分布，若 $\underline{\hspace{10cm}}$，则 $\overline{X}_n\xrightarrow{\;P\;}E(X)$
  
  • 即：对任意 $\varepsilon>0$，$\underline{\hspace{20cm}}$
  • 推论： $\{X_n\}$ 独立同分布，若 $\underline{\hspace{10cm}}$，则 $\frac{1}{n}\sum\limits_{i=1}^nX_i^k\xrightarrow{\;P\;}E(X^k)$
• 独立同分布的中心极限定理：$\{X_n\}$ 独立同分布，若 $\underline{\hspace{10cm}}$，则 $\underline{\hspace{10cm}}\stackrel{\text{近似}}{\sim}N(0,1)$
• De Moivre Laplace 定理：若 $\eta_n\sim b(n,p)$，则 $\underline{\hspace{15cm}}\stackrel{\text{近似}}{\sim}N(0,1)$

---

7. 抽样分布

• $\chi^2$-分布：$\bbox[lightgreen]{\chi^2=\sum\limits_{i=1}^n[N(0,1)]^2\sim\chi^2(n)}$
• t-分布：$\bbox[lightgreen]{T=\frac{N(0,1)}{\sqrt{\chi^2(n)/n}}\sim t(n)}$
• F-分布：$\bbox[lightgreen]{F=\frac{\chi^2(m)/m}{\chi^2(n)/n}\sim F(m,n)}$
• 以上的记号不是规范的写法，只是为了方便记忆，注意不要在答题时这样书写！
• 以上构造中，所有不同的随机变量必须是相互独立的！

---

统计量

• 样本均值 $\overline{X}$
  
  • $\bbox[yellow]{\sum\limits_{i=1}^n(X_i-\overline{X})=\underline{\hspace{3cm}}}$
  • $\sum\limits_{i=1}^n(X_i-\overline{X})^2=\min\limits_c\sum\limits_{i=1}^n(X_i-c)^2$
• 样本方差 $\bbox[yellow]{S^2=\underline{\hspace{10cm}}}$，$\bbox[yellow]{E(S^2)=\underline{\hspace{5cm}}}$

---

抽样分布定理

• 设 $X_1,X_2,...,X_n$ 为来自 $N(\mu,\sigma^2)$ 的样本，则
  
  • $\bbox[yellow]{\overline{X}\sim \underline{\hspace{8cm}}}$
  • $\bbox[yellow]{\frac{(n-1)S^2}{\sigma^2}=\frac{n\tilde{S}^2}{\sigma^2}\sim\underline{\hspace{8cm}}}$
  • $\overline{X}$ 和 $S^2$ 相互独立

---

$\chi^2$ 分布

• $\bbox[lightgreen]{\chi^2(m)+\chi^2(n)\sim\chi^2(m+n)}$
• $\bbox[yellow]{E(\chi^2)=\underline{\hspace{5cm}},\; D(\chi^2)=\underline{\hspace{5cm}}}$
• $\bbox[yellow]{\frac{\sum\limits_{i=1}^{n}(X_i-\mu)^2}{\sigma^2}\sim \underline{\hspace{5cm}}}$
• $\bbox[yellow]{\frac{\sum\limits_{i=1}^{n}(X_i-\overline{X})^2}{\sigma^2}\sim\underline{\hspace{5cm}}}$

---

重要例题：设 $X_i\sim N(0,1)\;(i=1,2,3,4)$ 相互独立，问 $\frac12 \left(X_1-X_2\right)^2+\frac12 \left(X_3+X_4\right)^2$ 服从什么分布？

---

t-分布

• $\bbox[lightgreen]{\lim\limits_{n\to\infty}t(n)=N(0,1)}$
• $t_{\alpha}(n)=-t_{1-\alpha}(n)$
• $\bbox[yellow]{\frac{\overline{X}-\mu}{S/\sqrt{n}}\sim \underline{\hspace{5cm}}}$
• $\bbox[yellow]{\frac{(\overline{X}-\overline{Y})-\left(\mu_{1}-\mu_{2}\right)}{S_{\omega}\underline{\hspace{5cm}}} \sim \underline{\hspace{5cm}}}$
  
  • 其中 $\bbox[yellow]{S_{\omega}=\underline{\hspace{8cm}}}$

---

F-分布

• $\bbox[yellow]{F_{\alpha}(m,n)=\frac{1}{F_{1-\alpha}(n,m)}}$
• $\bbox[yellow]{\frac{S_{1}^{2} / \sigma_{1}^{2}}{S_{2}^{2} / \sigma_{2}^{2}}=\frac{\frac{1}{n-1}\sum\limits_{i=1}^{n}(X_i-\overline{X})^2 / \sigma_{1}^{2}}{\frac{1}{m-1}\sum\limits_{j=1}^{m}(Y_j-\overline{Y})^2 / \sigma_{2}^{2}} \sim \underline{\hspace{5cm}}}$
• $\bbox[yellow]{\frac{\frac{1}{n}\sum\limits_{i=1}^{n}(X_i-\mu_1)^2 / \sigma_{1}^{2}}{\frac{1}{m}\sum\limits_{j=1}^{m}(Y_j-\mu_2)^2 / \sigma_{2}^{2}} \sim \underline{\hspace{5cm}}}$

---

8. 点估计

• 评价准则
  
  • 无偏性：$\underline{\hspace{10cm}}$
  • 有效性：均方误差 $\bbox[yellow]{r\left(\hat{\theta}\right)=\underline{\hspace{10cm}}}$
    
    • 对于无偏估计 $r\left(\hat{\theta}\right)=\underline{\hspace{10cm}}$
  • 相合性: $\hat{\theta}_n\xrightarrow{\;P\;}\theta$
    
    • Chebyshev 不等式: $\underline{\hspace{10cm}}$

---

矩估计

• 设 $X$ 的 pmf/pdf 为 $f(x;\theta_1,\ldots,\theta_m)$
• 令 $\bbox[yellow]{E(X^k)=\frac{1}{n}\sum\limits_{i=1}^n\left(X_i\right)^k,\;k=1,2,\ldots,m}$
  
  • 有多少个未知参数就列多少个方程
• 解方程组得到 $\hat{\theta}_1,\ldots,\hat{\theta}_m$

---

最大似然估计

• 似然函数 $\bbox[yellow]{L(\theta)=\prod_{i=1}^{n}f(x_i;\theta)}$
• 求 $L(\theta)$ 的最大值点
  
  • 令 $\bbox[yellow]{\frac{\mathrm{d}}{\mathrm{d}\theta}\ln L(\theta)=0}$，解出 $\hat{\theta}$
  • 如果驻点不存在，则考虑 $\theta$ 的取值范围的边界点
• 重要例题：求 $U(a,b)$ 中参数 $a,b$ 的最大似然估计.

---

9. 区间估计

$$\bbox[yellow]{P\left\{\underline{\theta}\leq\theta\leq\overline{\theta}\right\}\geq 1-\alpha}$$

• 枢轴变量
  
  • 包含 $\theta$，但不包含其他未知参数
  • 分布与 $\theta$ 无关

---

单正态总体均值和方差的区间估计

---

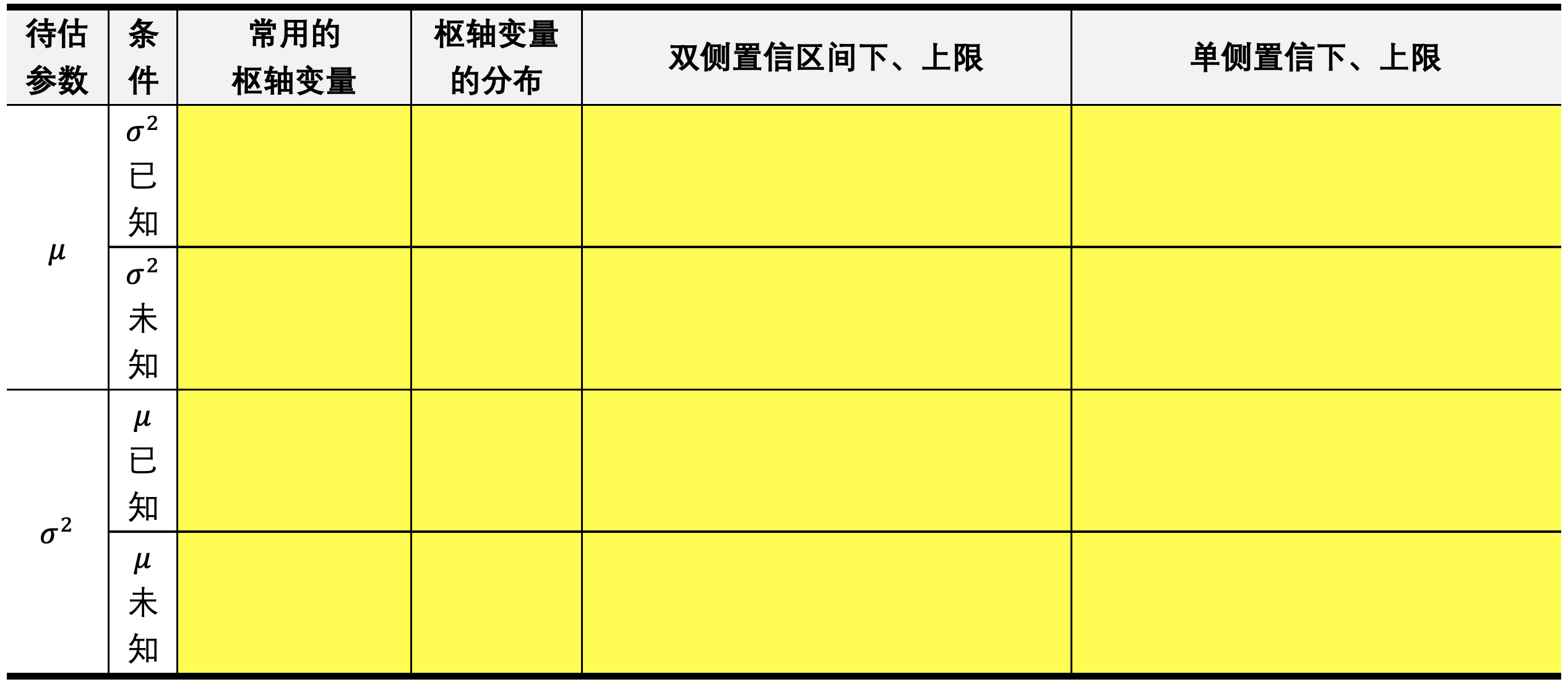
双正态总体均值差和方差比的区间估计

---

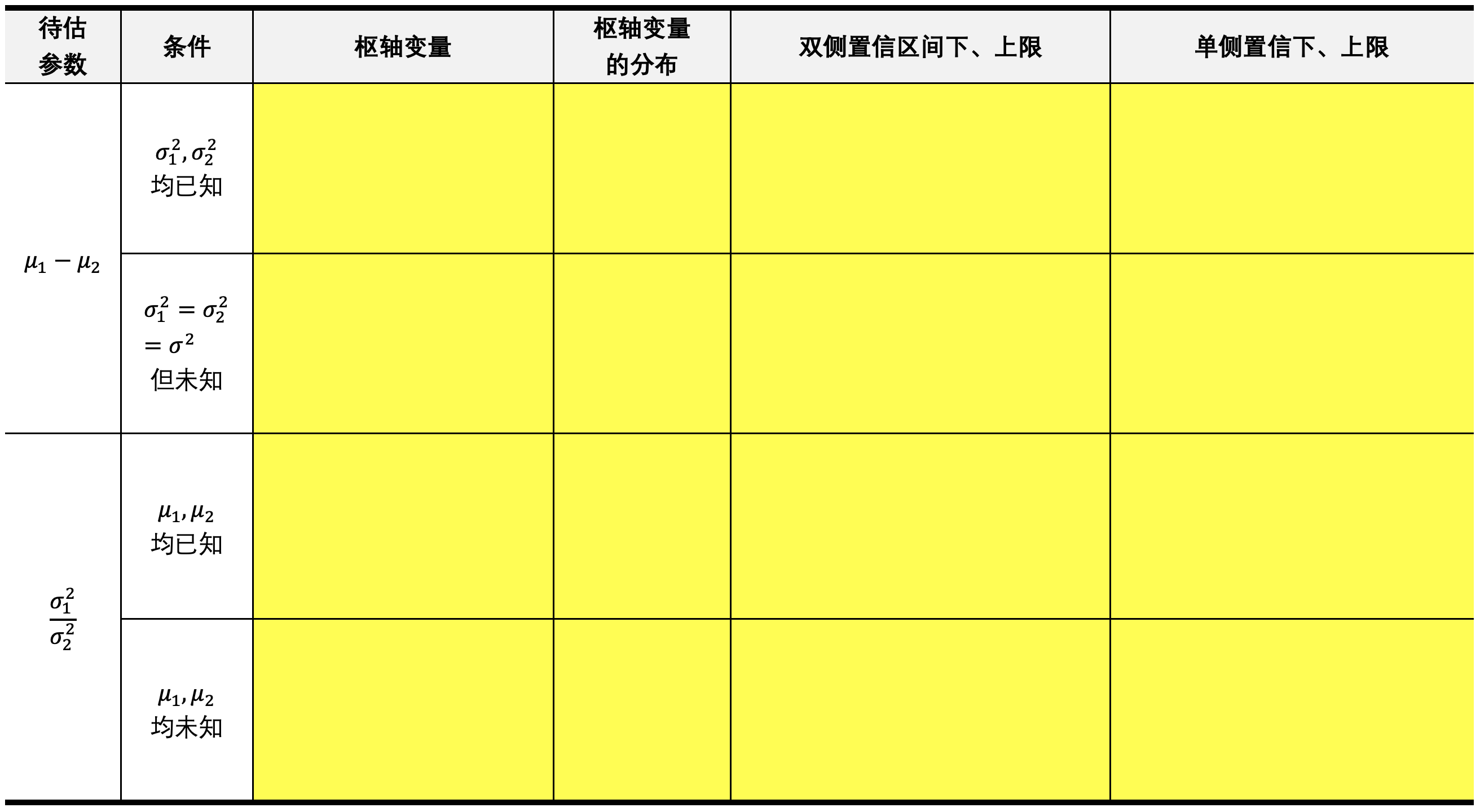
10. 假设检验

• 提出假设
  
  • 原假设一般是需要保护的假设或与直观判断结果相反的假设
  • 原假设中应该包含等号
• 从备择假设出发，确定拒绝域的形式
• 选择检验统计量，由检验原则一出发，推导拒绝域
  
  • 将原假设一律作为简单假设处理
• 代入观测值计算，给出结论

---

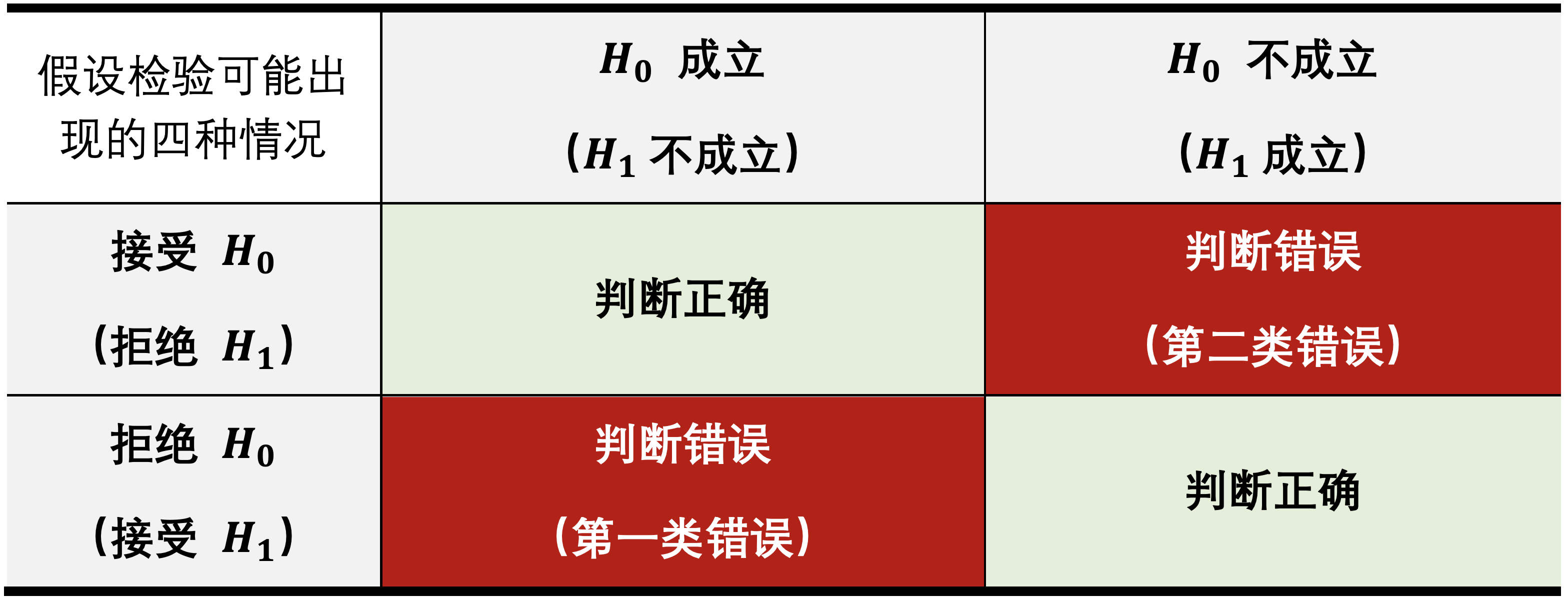
• I 类风险： $\bbox[yellow]{P\{\text{拒绝 }H_0|H_0\text{ 成立}\}}$
• 在样本容量给定的情况下，优先控制 I 类风险，不管 II 类风险

---

单正态总体均值的检验

---

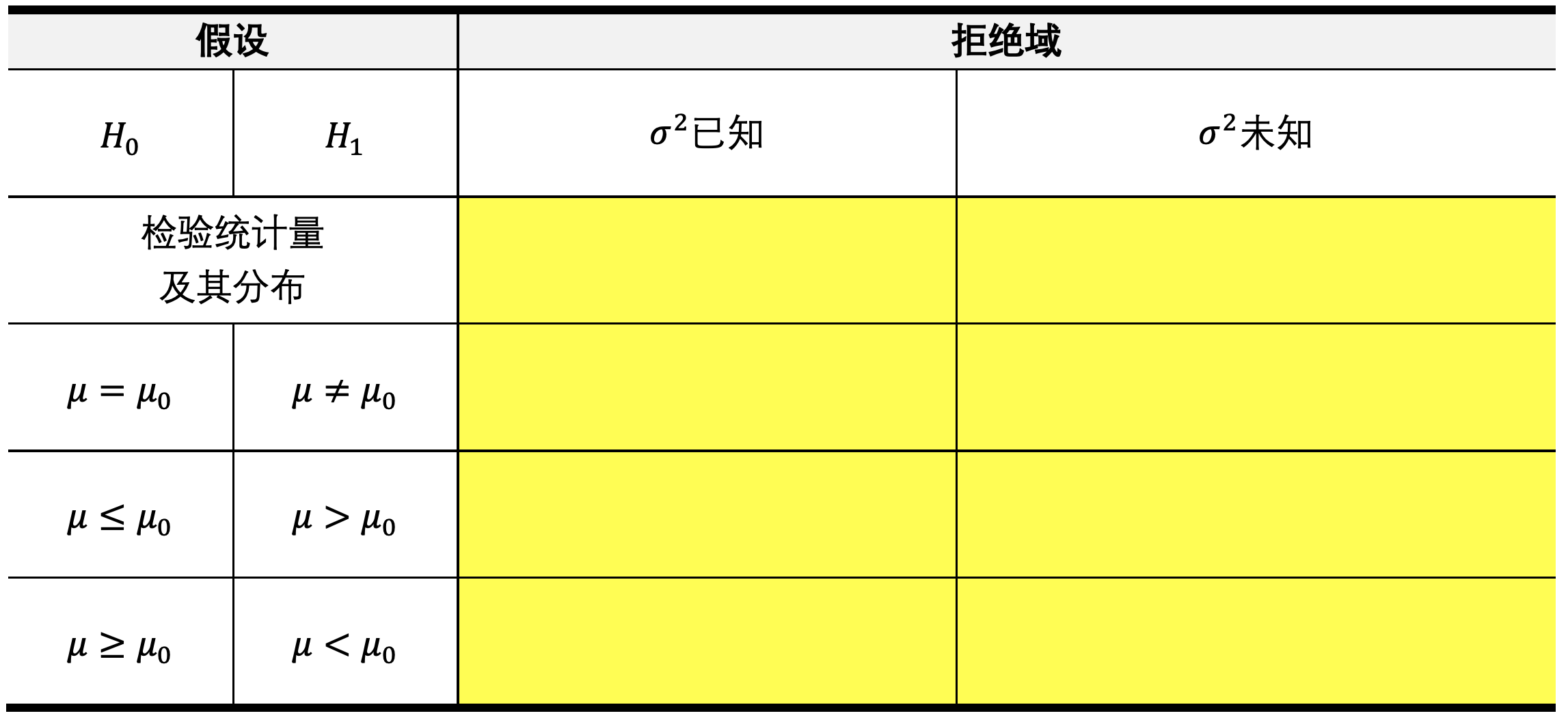
单正态总体方差的检验

---

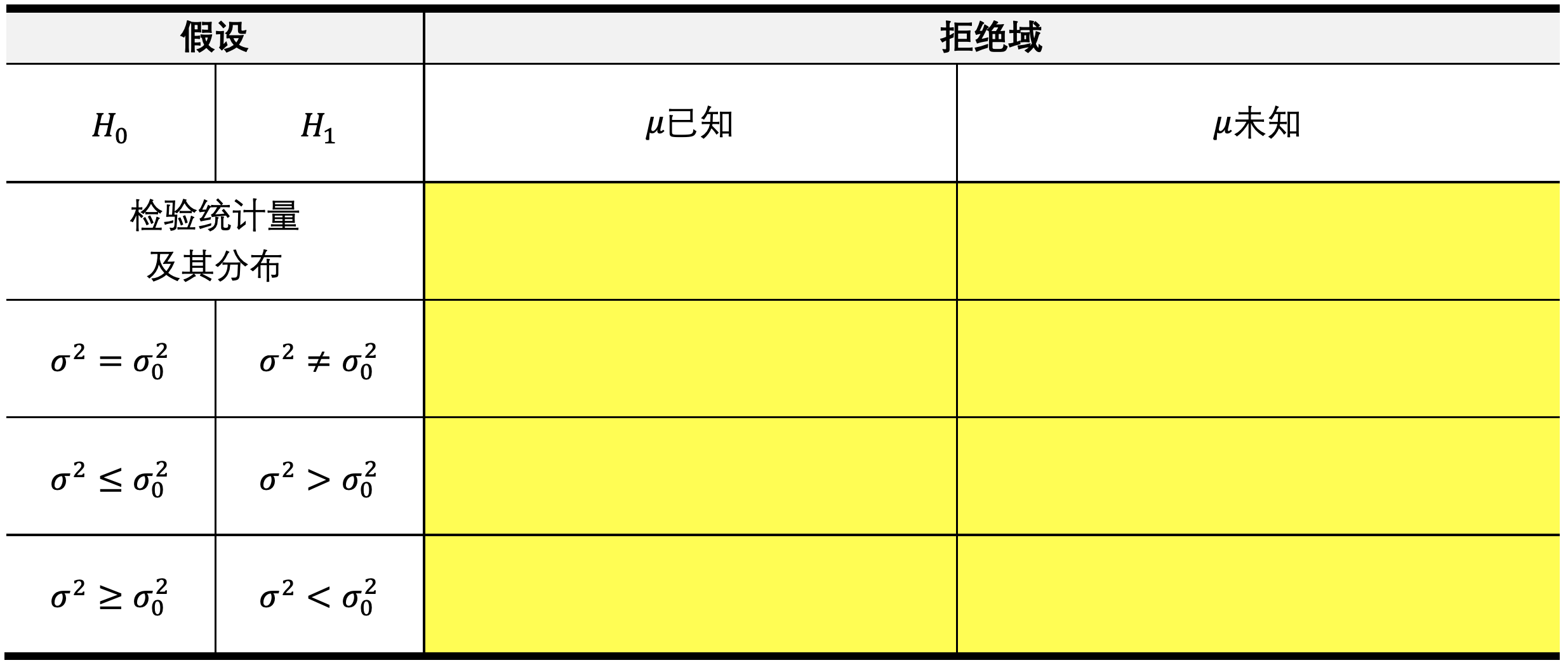
双正态总体均值差的检验

---

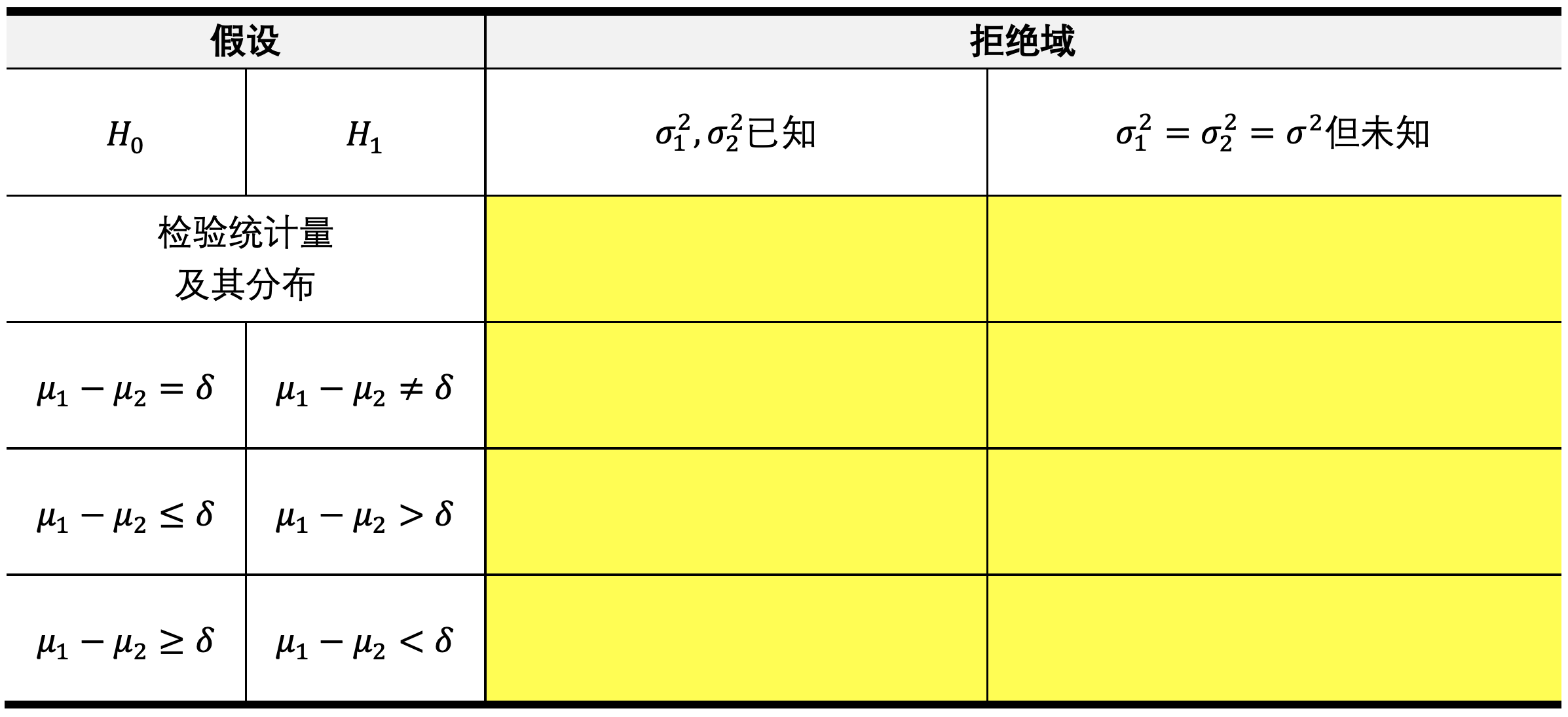
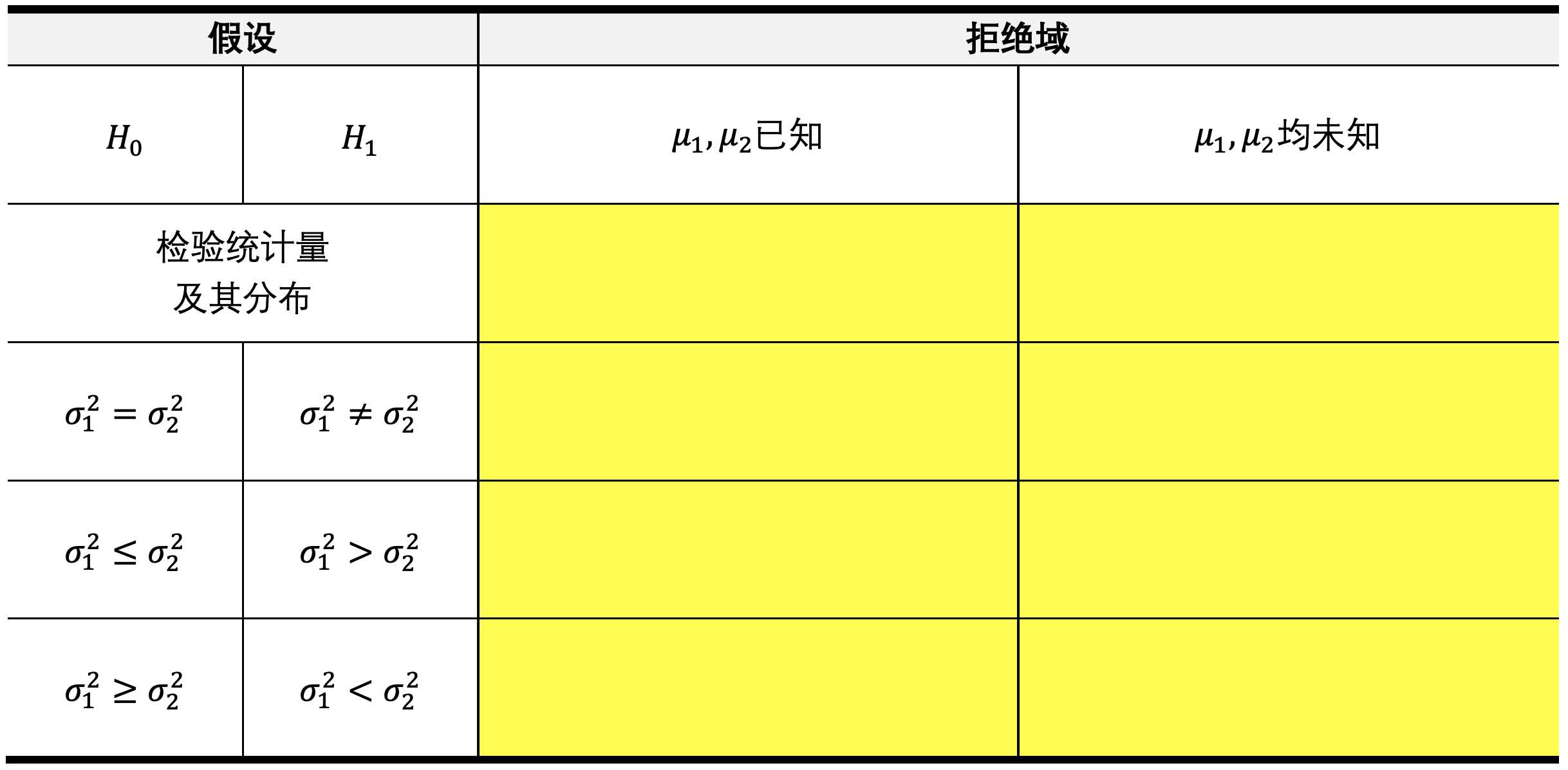
双正态总体方差比的检验

---

11. 一元线性回归

• 一元线性回归模型 $\bbox[yellow]{\begin{cases} y=\beta_0+\beta_1x+\varepsilon\\ E(\varepsilon)=0,\;D(\varepsilon)>0 \end{cases}}$
• 回归系数的$\underline{\hspace{3cm}}$估计
  
  • $\bbox[yellow]{\hat{\beta}_1=\dfrac{L_{xy}}{L_{xx}}=\sum\limits_{i=1}^n\underline{\hspace{5cm}}y_i}$
  • $\bbox[yellow]{\hat{\beta}_0=\underline{\hspace{5cm}}=\sum\limits_{i=1}^n\underline{\hspace{5cm}}y_i}$
• 经验回归方程：$\hat{y}=\hat{\beta}_0+\hat{\beta}_1x$

---

缩写记号

• $\bbox[yellow]{L_{xx}=\underline{\hspace{10cm}}}$
• $\bbox[yellow]{L_{xy}=\underline{\hspace{10cm}}}$
• 均方误差 $\bbox[yellow]{Q(\beta_0,\beta_1)=\underline{\hspace{10cm}}}$
• 残差 $\bbox[yellow]{Q_e=\underline{\hspace{10cm}}}$
• 剩余方差 $\bbox[yellow]{\hat{\sigma}^2_e=\underline{\hspace{10cm}}}$

---

重要性质

1. $\bbox[yellow]{E(\hat{\beta}_1)=\underline{\hspace{10cm}}}$
2. $\bbox[yellow]{E(\hat{\beta}_0)=\underline{\hspace{10cm}}}$
3. $\mathrm{Cov}(\overline{y},\hat{\beta}_1)=0$.
4. $\bbox[yellow]{D(\hat{\beta}_1)=\underline{\hspace{10cm}}}$
5. $\bbox[yellow]{D(\hat{\beta}_0)=\underline{\hspace{10cm}}}$
6. $\bbox[yellow]{E(Q_e)=\underline{\hspace{10cm}}}$

---

正态线性模型

• 在一元线性回归模型中增加新的假设：$\bbox[yellow]{\underline{\hspace{10cm}}}$ 即可得到正态线性模型
• 性质
  
  • $\bbox[yellow]{y_i\sim\underline{\hspace{10cm}}}$
  • 在正态线性模型下，$\beta_0$、$\beta_1$ 的 LSE 就是 MLE
  • $\sigma^2$ 的无偏估计是 $\bbox[yellow]{\underline{\hspace{10cm}}}$
  • $\bbox[yellow]{\dfrac{Q_e}{\sigma^2}\sim\sim\underline{\hspace{10cm}}}$
  • $\bbox[yellow]{\dfrac{\hat{\beta}_1-\beta_1}{\hat{\sigma}_e^2/\sqrt{L_{xx}}}\sim\underline{\hspace{10cm}}}$

---

EOF