第三讲 等可能概型

概率论与数理统计 讲义 NUDT 2023SP

---

3.1 古典概型

古典概型 (Classical Probability Model) 是一种关于有限多个等可能结果的概率模型.

• 例: 掷一个骰子(🎲), 观察其点数
  
  • 假设骰子是均匀的，即出现每个点数的概率相同.
  • 样本空间: $\Omega=\{1,2,3,4,5,6\}$。
  • 简单事件的概率 $P(\{i\})=1/6,\;i=1,2,...,6$.
  • 设事件 $A$ 表示得到的点数比 $4$ 大，$A=\{5,6\}$
  • 由概率的有限可加性，$P(A)=P(\{5,6\})=P(\{5\})+P(\{6\})=\frac13$

---

例：抛硬币试验

掷两个硬币，观察其正反面，定义事件 $A$ 为两个硬币朝上的面不同，求 $P(A)$.

• 解：
  
  • 假设两个硬币都是均匀的，也即得到两面（分别记为 $H$ 和 $T$）的几率相同.
  • 样本空间 $\Omega=\{HH,HT,TH,TT\}$，其中每个简单事件出现的概率为 $1/4$.
  • 事件 $A=\{HT,TH\}$.
  • $P(A)=P(\{HT\})+P(\{TH\})=\frac12$.

---

3.2 古典概型的概率计算公式

设 $\Omega=\{\omega_1,\omega_2,...,\omega_{n}\}$，由等可能假设 $P(\{\omega_i\})=\frac{1}{n},\;i=1,2,...,n$.

若事件 $A=\{\omega_{i_1},\omega_{i_2},...,\omega_{i_k}\}$，则由概率的有限可加性

$$P(A)=\sum\limits_{j=1}^kP(\{\omega_{i_j}\})=\sum\limits_{j=1}^k\frac{1}{n}=\frac{k}{n}.$$

一般地，记 $n(\Omega)$ 为 $\Omega$ 的总点数，$n(A)$ 为事件 $A$ 包含的不同样本总数（称为 $A$ 的有利场合数），则

$$P(A)=\frac{n(A)}{n(\Omega)}.$$

不难发现

• 样本计数是求解古典概型问题的关键
  
  • 加法原理和乘法原理
  • 排列与组合

---

加法原理

如果导致一个事件发生共有 $n$ 类不同的方法/途径，每类方法/途径又有 $m_i\;(i=1,...,n)$ 种不同的子方法/途径，则该事件总的样本点数为

$$\sum\limits_{i=1}^nm_i$$

---

乘法原理

如果导致一个事件发生需要 $n$ 个步骤/阶段，且每个步骤/阶段又有 $m_i\;(i=1,...,n)$ 种不同的方法/途径，则该事件总的样本点数为

$$\prod\limits_{i=1}^nm_i$$

---

乘法原理的另一种表述

如果事件 $A$ 中的样本可以表示为类似 $(a,b)$ 的 二元组形式，且

• $a$ 有 $n_a$ 种不同的取值（结果），
• 对于 $a$ 的每一个取值（结果），$b$ 与之对应的都有 $n_b$ 种不同取值（结果），
• 则 $A$ 的有利场合数为 $n(A)=n_an_b$.

---

例：摸球问题 1

袋中有 $r$ 个红球和 $b$ 个黑球. 所有的球外形和材质完全相同. 无放回地依次从袋中取出两个球，计算：

• （1）两个球都是红球的概率.
• （2）两个球颜色不同的概率.
• （3）如果改为有放回地摸球，以上两问的结果分别是什么？

---

解: （1）两个球都是红球的概率.

第一次取球, 可选的球有 $r+b$ 个. 第二次取球, 可选的球有 $r+b-1$ 个. 因此样本空间的总点数 $n(\Omega)=(r+b)(r+b-1)$.

对于事件 $A:$ 恰好取到两个红球. 第一步可选的球有 $r$ 个, 第二步可选的球有 $r-1$ 个. 因此 $A$ 的有利场合数 $n(A)=r(r-1)$.

综上，

$$P(A)=\frac{n(A)}{n(\Omega)}=\frac{r(r-1)}{(r+b)(r+b-1)}.$$

---

（2）两个球颜色不同的概率.

总点数 $n(\Omega)=(r+b)(r+b-1)$.

事件 $B:$ 两个球颜色不同，可划分为两个互斥的事件：$B_1:$ 第一次摸到红球，第二次摸到黑球，$B_2:$ 第一次摸到黑球，第二次摸到红球. 由乘法原理，事件 $n(B_1)=n(B_2)=rb$.

故

$$P(B)=P(B_1)+P(B_2)=\frac{2rb}{(r+b)(r+b-1)}.$$

---

（3）有放回到情况。

两个球都为红球的概率 $P(A)=\left(\frac{r}{r+b}\right)^2$.

两个球颜色不同的概率 $P(A)=\frac{2rb}{(r+b)^2}$.

---

排列与组合

• 组合(Combination): 从 $n$ 个元素中取出 $k$ 个，构成一个集合.

  • 组合数: $\bbox[yellow]{\binom{n}{k}=C_n^k=\frac{n!}{(n-k)!k!}}$
  • 例: 从编号为 $0,1,2,\ldots,9$ 的几个人中选出 $4$ 人组成一个小分队.

• 排列 (Permutation): 从 $n$ 个元素中取出 $k$ 个，构成一个序列.

  • 排列数: $\bbox[yellow]{A_n^k=k!\binom{n}{k}=\frac{n!}{(n-k)!}}$.
  • 例: 从 $0,1,2,\ldots,9$ 中选出 $4$ 个不同的数构成一个口令.

---

例： 摸球问题 2

袋中有 $r$ 个红球和 $b$ 个黑球. 所有的球外形和材质完全相同. 无放回地依次从袋中取出 $n\;(n\leq r+b)$ 个球，求其中恰有 $k\;(k\leq\min\{n,r\})$ 个红球的概率.

---

解法 1:

• 定义本问题的样本为一个由红球和黑球所构成的长度为 $n$ 的序列.
• 因为构造一个样本需要 $n$ 步，且每一步无放回，因此样本空间的总点数等于排列数 $A_{r+b}^n$.
• 记事件 $R_k$ 为恰好取了 $k$ 个红球.
• 为了得到 $R_k$ 中的一个样本，我们需要在 $k$ 个步骤中选到红球，剩下的 $n-k$ 个步骤中选到黑球.

---

• 具体来说，我们可以通过以下步骤来得到 $R_k$ 中的一个样本：
  
  • 首先在 $n$ 个步骤中选择 $k$ 个，用于取红球，共有 $C_n^k$ 个不同的选择方案；
  • 然后按照以上步骤的设定，依次在 $r$ 个红球中选择 $k$ 个，在 $b$ 个黑球中选择 $n-k$个，共有 $A_r^kA_{b}^{n-k}$ 个不同的选择方案；
• 综上，$R_k$ 的有利场合数为，$C_n^kA_r^kA_{b}^{n-k}$.
• $P(R_k)=\frac{C_n^kA_r^kA_{b}^{n-k}}{A_{r+b}^n}=\frac{\frac{n!}{k!(n-k)!}\frac{r!}{(r-k)!}\frac{b!}{(b-n+k)!}}{\frac{(r+b)!}{(r+b-n)!}}=\frac{\frac{r!}{(r-k)!k!}\frac{b!}{(b-n+k)!(n-k)!}}{\frac{(r+b)!}{(r+b-n)!n!}}=\frac{C_r^kC_{b}^{n-k}}{C_{r+b}^n}$

---

解法 2:

• 定义本问题的样本为一个由红球和黑球所构成的大小为 $n$ 的集合.
• 从 $r+b$ 个球中选取 $n$ 个，共有 $C_{r+b}^n$ 种不同的方法，也即总样本点数.
• 记事件 $R_k$ 为恰好取了 $k$ 个红球.
• $R_k$ 中的任意一个样本，可以视为两个集合的并集.
  
  • 这两个集合分别是从 $r$ 个红球中选择的 $k$ 的红球，和从 $b$ 个黑球中选择的 $n-k$ 个黑球.

---

• 从 $r$ 个红球中选择 $k$ 个，共有 $C_r^k$ 种不同的组合.
• 从 $b$ 个黑球中选择 $n-k$ 个，共有 $C_b^{n-k}$ 种不同的组合.
• 综上，$R_k$ 中的样本共有 $C_r^kC_b^{n-k}$ 种不同的可能，也即 $R_k$ 的有利场合数.
• 因此, $P(R_k)=\frac{C_r^kC_{b}^{n-k}}{C_{r+b}^n}$.

---

例: 生日问题

教室中有 $n$ 个学生，求其中至少有两个学生生日相同的概率.

• 放球问题：将 $n$ 个球随机放置到 $m\;(m>n)$ 个盒子中，求至少有两个球放在同一个盒子中的概率.

---

放球问题的解答：

• 定义事件 $B$ 为每个盒子中最多有一个球.
  
  • 要求的概率为 $P(\overline{B})=1-P(B)$.
• 一般情况下，完成一次放置可分为 $n$ 个步骤，每一步都有 $m$ 个盒子可选，故总点数为 $m^n$.
• 要满足事件 $B$ 的要求，则每一步不能再选择已经有球的盒子，因此 $B$ 的有利场合数 $n(B)=A_m^n$.
• 综上，所求概率 $P(\overline{B})=1-P(B)=1-\frac{A_m^n}{m^n}$.

---

生日问题的解答：

• 定义事件 $B$ 为每个学生的生日都不同.
• 将学生的生日视为球，不同的日期视为盒子.
• 则所求概率 $P\left(\overline{B}\right)=1-P(B)=1-\frac{A_{365}^n}{365^n}$.
• 计算结果

$$\begin{array}{c|ccccccc} n & 20 & 25 & 30 & 40 & 50 & 100 & 200\\ \hline 1-P & 0.41 & 0.57 & 0.71 & 0.89 & 0.97 & 0.99 & 0.9999997 \end{array}$$

---

3.3 几何概型

例：行动的同步

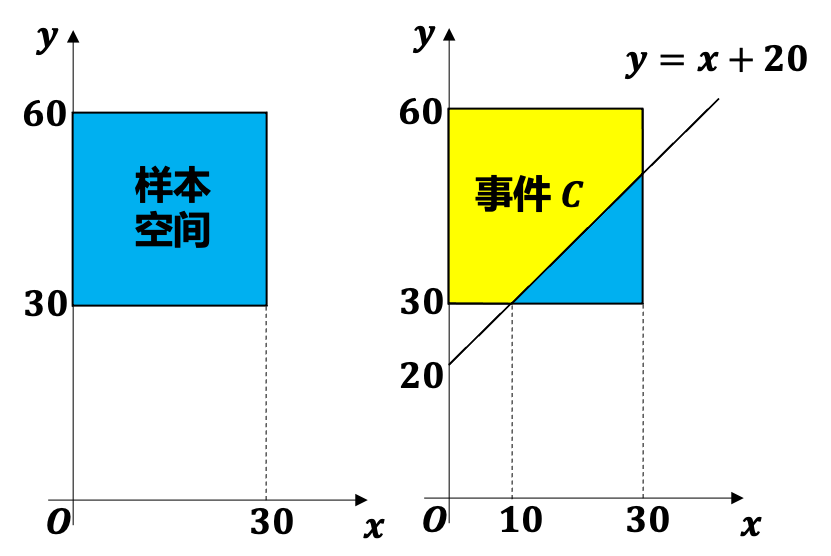
在一次军事行动中，工兵营负责为坦克部队在某条河上搭建浮桥. 工兵营预计上午 7:00-7:30 之间到达河边，搭桥需要 20 分钟. 坦克部队预计上午 7:30-8:00 之间到达河边. 求坦克部队到达河岸后可以立即开始过河的概率.

---

解:

• 如图，以上午 7:00 坐标原点建立坐标系.
• 设 $x,y$ 分别表示工兵营和坦克部队到达的时间.
• 定义事件 $C$ 为坦克部队到达河岸时浮桥已建好. $C$ 发生的当且仅当
  
  • $\left\{ \begin{array} { c } { x + 20 \leq y } \\ { 0 \leq x \leq 30 } \\ { 30 \leq y \leq 60 } \end{array} \right.$
• 计算 $C$ 的样本空间对应的面积之比，即得 $P(C)= \frac { 30 ^ { 2 } - 20 ^ { 2 } / 2 } { 30 ^ { 2 } } = \frac { 7 } { 9 }$.

---

例：Buffon 投针

在一张纸上以牙签的长度为间距，画出一系列平行线. 然后将牙签随机丢到纸上，求牙签与某一条平行线相交的概率.

---

分析:

• 发生相交当且仅当 : $d\leq\frac12\sin\theta$
• 样本空间: $\Omega=\left\{(d,\theta)\bigg|0\leq d\leq \frac12, 0\leq\theta\leq\pi/2\right\}$

---

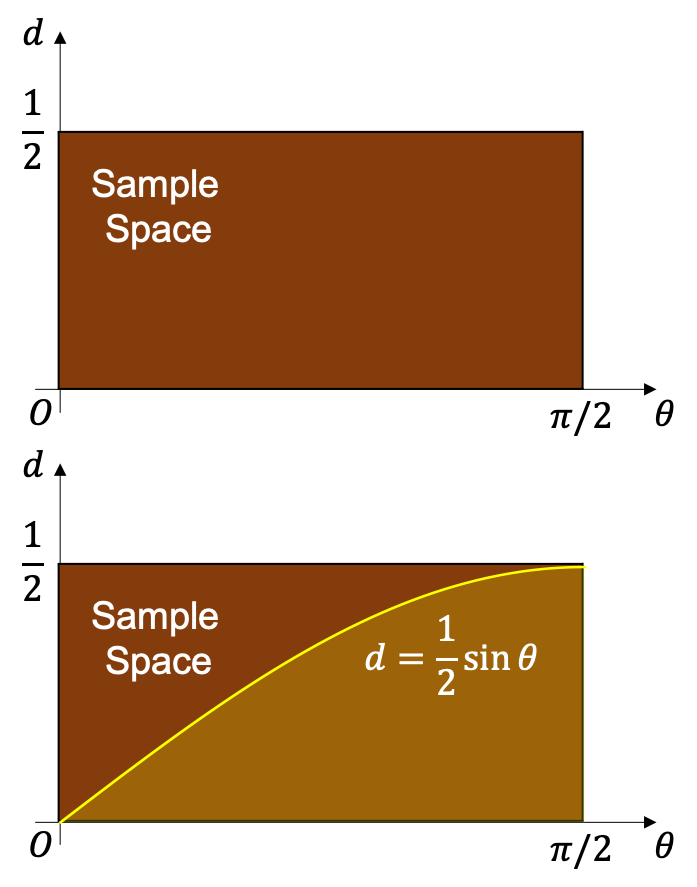
解:

• 样本空间的面积: $\frac{\pi}{4}$
• 发生相交的事件对应的面积
  
  • $\int_0^{\pi/2}\frac12\sin\theta\mathrm{d}\theta=\frac12$
• 发生相交的概率 $=2/\pi$.

---

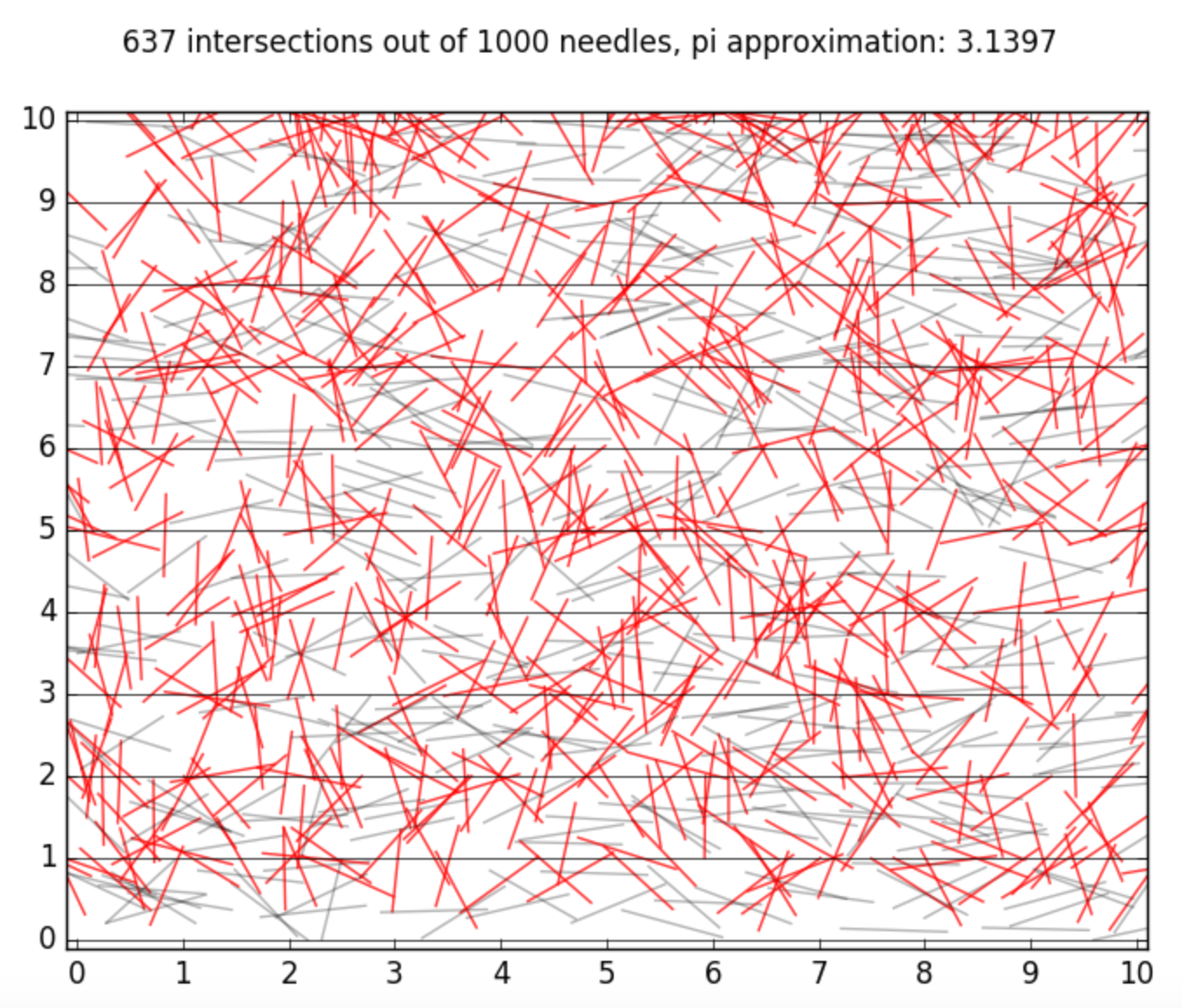
仿真

---

几何概型

• 特征：
  
  • 样本空间中包含无穷多个样本点.
  • 每个简单事件发生的概率均为 $0$.
• 记 $\mu(A)$ 为对事件 $A$ 的某种几何度量 (例如：面积、体积、夹角，...) ，则 $A$ 发生的概率
  
  • $P(A)=\frac{\mu(A)}{\mu(\Omega)}$

---

小结

• 古典概型：$P(A)=\frac{n(A)}{n(\Omega)}$
  
  • 重点 & 难点：样本点的计数
    
    • 排列、组合、乘法规则
    • 避免漏计、重复计
• 几何概型：$P(A)=\frac{\mu(A)}{\mu(\Omega)}$
  
  • 重点：使用几何模型模表达所述问题

---

Mathematics is the door and key to the sciences.
-- Roger Bacon

---

课堂思考

（匹配问题） 有 $n$ 个孩子，每人戴着一顶帽子. 如果他们将帽子都放在一起，然后每人随机从帽子堆中取一顶戴上，问至少有一人戴着自己的帽子的概率.

（匹配问题） 有 $n$ 个战士，每人的配枪都有专门的编号. 休息时，所有的枪集中存放在一起. 晚上紧急集合，每人来不及核对枪支编号，随机取走一支枪. 问至少有一人拿到了自己的枪的概率.