第十六讲 多维随机变量的函数的分布

概率论与数理统计 讲义 NUDT 2023SP

---

---

16.1 背景与问题

设下图中部件 I, II 的寿命分别为 rv $X,Y$

在不同的连接方式下，系统的寿命服从什么分布？

• 给定 rv $X,Y$ 的分布, 求它们的函数 $X+Y$, $\max\{X,Y\}$, $\min\{X,Y\}$ 的分布.

---

常见的问题

给定连续型 rv $(X,Y)$ 的 pdf $f(x,y)$

• 第 I 类问题: 设 $U=g(X,Y)$, 求 $U$ 的 pdf.
• 第 II 类问题: 设 $U=g_1(X,Y),V=g_2(X,Y)$, 求 $(U,V)$ 的 pdf.
• 回顾: 对连续型 rv $X$, 设 $Y=g(X)$, 若反函数 $h=g^{-1}$ 单调且可微, 则
  
  • $f_Y(y)=\left\{\begin{array}{cc}{\left|h^{\prime}(y)\right| \cdot f_{X}(h(y)),} & h(y)\in D \\ {0,} & {\text{其他}}\end{array}\right.$

---

16.2 第 I 类问题

已知 $(X,Y)$ 的 pdf $f(x,y)$，令 $U=g(X,Y)$, 求 $U$ 的 pdf $f_U(u)$.

• 思路:
  
  • $F_U(u)=P\{U\leq u\}=P\{g(X,Y)\leq u\}=\iint\limits_{g(x,y)\leq u}f(x,y)\mathrm{d}x\mathrm{d}y=\ldots=h(u)$
  • $f_U(u)=\frac{\mathrm{d}}{\mathrm{d}u}F_U(u)=\frac{\mathrm{d}}{\mathrm{d}u}h(u)$

---

两个随机变量和的分布

例：设 rv $X,Y$ 相互独立，且均服从 $\mathrm{Exp}(\lambda)$, 求 $U=X+Y$ 的 pdf.

• $(X,Y)$ 的 pdf
  
  • $f(x, y)=f_X(x)f_Y(y)=\left\{\begin{array}{cc}{\lambda^{2} \mathrm{e}^{-\lambda(x+y)}} & {x>0, y>0} \\ {0} & {\text{其他}}\end{array}\right.$
• $u<0$ 时, $x+y<u$ 意味着至少 $x,y$ 之一小于零，因此 $F_U(u)=F_X(x)F_Y(y)=0$, 进而 $f_U(u)=0$.
• 若 $u>0$, $F_{U}(u)=P\{X+Y \leq u\}=\iint\limits_{x+y\leq u}f(x,y)\mathrm{d} x \mathrm{d} y$

---

如图所示

$$\begin{aligned} F_{U}(u) &=P\{X+Y \leq u\}\\ &=\iint_D\lambda^{2} \mathrm{e}^{-\lambda(x+y)} \mathrm{d} x \mathrm{d} y \\ &=\int_{0}^{u} \mathrm{d} y \int_{0}^{u-y} \lambda^{2} \mathrm{e}^{-\lambda(x+y)} \mathrm{d} x \\ &=\lambda \int_{0}^{u}\left(\mathrm{e}^{-\lambda y}-\mathrm{e}^{-\lambda u}\right) \mathrm{d} y \\ &=1-(1+\lambda\mu)\mathrm{e}^{-\lambda u} \end{aligned}$$

综上

$$F_{U}(u)=\left\{\begin{array}{cc} 1-(1+\lambda u)\mathrm{e}^{-\lambda u}& u>0 \\ 0& u \leq 0\end{array}\right.$$

进而

$$f_{U}(u)=\frac{\mathrm{d}}{\mathrm{d}u}F_U(u)=\left\{\begin{array}{cc} \lambda^{2} u \mathrm{e}^{-\lambda u}& u>0 \\ 0& u \leq 0\end{array}\right.$$

---

例：从指数分布到 Gamma 分布

设 $X_1,X_2,\ldots,X_n$ 相互独立，且均服从 $\mathrm{Exp}(\lambda)$, 证明

$$U_n=\sum_{i=1}^{n}X_i\sim\Gamma\left(n,\frac{1}{\lambda}\right).$$

• $f_{U_n}(u)=\left\{\begin{array}{cc}\frac{\lambda^nu^{n-1}}{(n-1) !}\mathrm{e}^{-\lambda u} & u>0\\ 0 & \text{其他}\end{array}\right.$

---

16.3 第 II 类问题

已知 $(X,Y)$ 的 pdf $f(x,y)$，令 $U=g_1(X,Y)$, $V=g_2(X,Y)$, 求 $(U,V)$ 的 pdf $f_{UV}(u,v)$.

• 思路：
  
  • $F_{U V}(u, v) =P\left\{g_{1}(X, Y) \leq u, g_{2}(X, Y) \leq v\right\}$
  • $f_{U V}(u, v)=\frac{\partial^2}{\partial u\partial v}F_{UV}(u,v)=h(u, v)$

---

随机向量的可逆变换的分布

定理: 已知 rv $(X,Y)$ 的 pdf $f(x,y)$ , 若变换 $\left\{\begin{array}{l}U=g_1(X,Y)\\ V=g_2(X,Y)\end{array}\right.$ 可微且有唯一的逆变换 $\left\{\begin{array}{l}X=h_1(U,V)\\ Y=h_2(U,V)\end{array}\right.$, 则 $(U,V)$ 的 pdf 为

$$f_{U V}(u, v)=\left\{\begin{array}{cc}{|J|\cdot f\left(h_{1}(u, v), h_{2}(u, v)\right)} & {(u, v)\text{取值有效}} \\ {0} & {\text {其他}}\end{array}\right.$$

其中 Jacobi 行列式 $J=\frac{\partial(x,y)}{\partial(u,v)}$.

---

Jacobi 行列式

给定变换 $\left\{\begin{array}{l}u=g_1(x,y)\\ v=g_2(x,y)\end{array}\right.$, 其中 $g_1,g_2$ 均可微,

$$J=\frac{\partial(x,y)}{\partial(u,v)}=\left|\begin{array}{cc}\frac{\partial x}{\partial u} & \frac{\partial y}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v}\end{array}\right|$$

• $J\ne 0$, 当且仅当存在以上变换的逆变换 $\left\{\begin{array}{l}z=h_1(u,v)\\ y=h_2(u,v)\end{array}\right.$
• 若 $J\ne 0$, $\frac{1}{J}=\frac{\partial(u,v)}{\partial(x,y)}$

---

例：极坐标系下的二维正态分布

设导弹落点的坐标 $(X,Y)$ 服从二维正态分布，其密度为

$$f(x, y)=\frac{1}{2 \pi \sigma^{2}}\exp\left(-\frac{x^{2}+y^{2}}{2 \sigma^{2}}\right),\; (x,y)\in\mathbb{R}^2.$$

求其对应的极坐标 $(R,\Theta)$ 的概率分布.

---

解： $\left\{\begin{array}{l}{x=r \cos \theta} \\ {y=r \sin \theta}\end{array}\right. \quad(r>0,0<\theta \leq 2 \pi)$ 可微且可逆. Jacobi 行列式

$$J=\frac{\partial(x, y)}{\partial(r, \theta)}=\left| \begin{array}{cc}{\cos \theta} & {-r \sin \theta} \\ {\sin \theta} & {r \cos \theta}\end{array}\right|=r$$

于是 $(R,\Theta)$ 的 pdf 为

$$\begin{aligned} f_{(R\Theta)}(r, \theta)&=f\left(h_{1}(r, \theta), h_{2}(r, \theta)\right) \cdot|J|\\ &=\left\{\begin{array}{cc}\displaystyle \frac{r}{2 \pi \sigma^{2}} \exp\left(-\frac{r^{2}}{2 \sigma^{2}}\right), & {r>0,0<\theta \leq 2 \pi} \\ {0,} & {\text {其他}}\end{array}\right. \end{aligned}$$

---

16.4 一些常用的函数及其分布

• 随机变量的和
• 随机变量的差与商
• 随机变量的最大值、最小值

---

16.4.1 随机变量和与卷积

问题：已知 rv $(X,Y)$ 的 pdf $f(x,y)$, 求 $U=X+Y$ 的 pdf.

• 令 $\left\{\begin{array}{l}u=x+y\\ v=y\end{array}\right.$, 逆变换 $\left\{\begin{array}{l}x=u-v\\ y=v\end{array}\right.$
• Jacobi 行列式 $J=\frac{\partial(x, y)}{\partial(u, y)}=\left| \begin{array}{rr}{1} & {-1} \\ {0} & {1}\end{array}\right|=1$
• $f_{U V}(u, v)=f(u-v, v)$
• $f_{U}(u)=\int_{-\infty}^{\infty} f(u-v, v) \mathrm{d} v=\int_{-\infty}^{\infty} f(v, u-v) \mathrm{d} v$

---

卷积

若 rv $X,Y$ 相互独立，则 $f(x,y)=f_X(x)\cdot f_Y(y)$, 进而

$$\begin{aligned} f_{U}(u) &=\int_{-\infty}^{\infty} f(u-v, v) \mathrm{d} v=\int_{-\infty}^{\infty} f(v, u-v) \mathrm{d} v \\ &=\int_{-\infty}^{\infty} f_{X}(u-v) f_{Y}(v) \mathrm{d} v=\int_{-\infty}^{\infty} f_{X}(v) f_{Y}(u-v) \mathrm{d} v \end{aligned}$$

• 以上最右端的公式称为 函数 $f_X,f_Y$ 的卷积 (convolution)，通常记为 $\left(f_{X} * f_{Y}\right)(u)$

---

卷积的几何意义

---

---

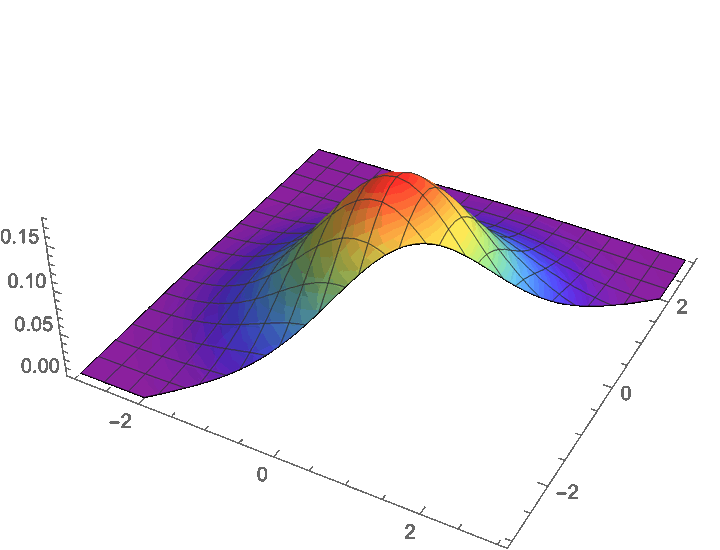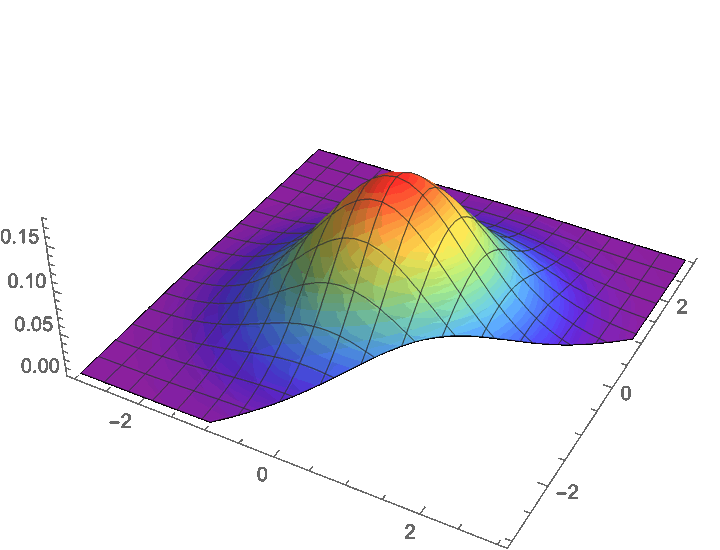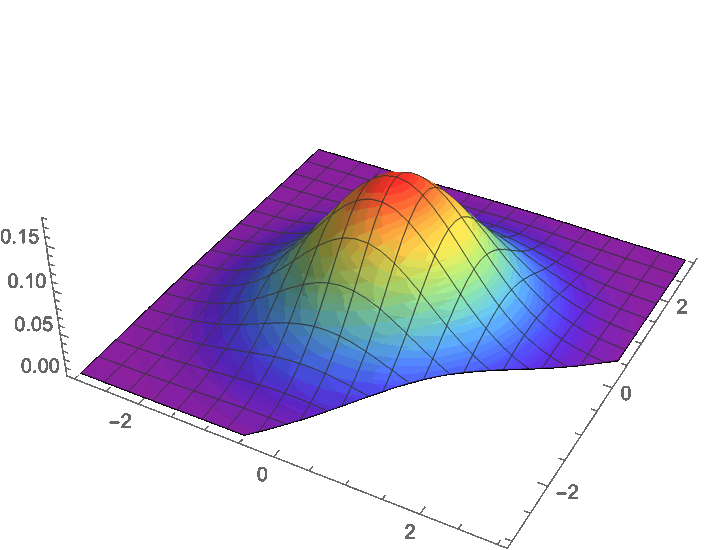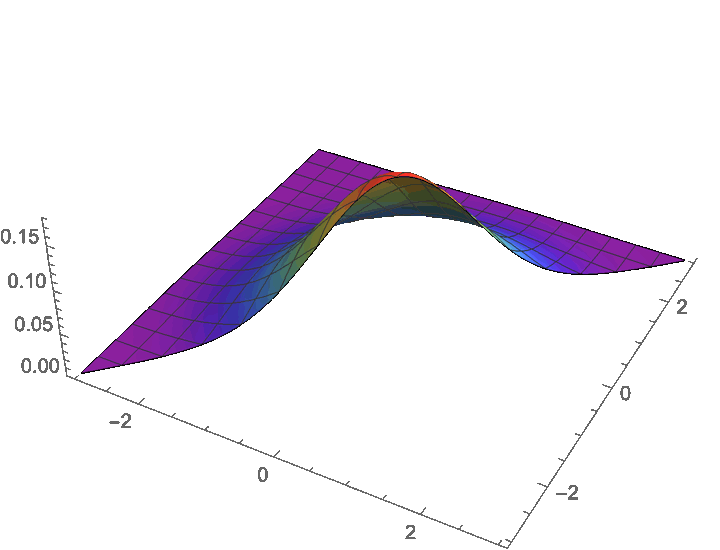
例：标准正态随机变量的和

设 rv $X,Y$ 相互独立，且均服从 $N(0,1)$, 求 $X+Y$ 的 pdf.

• $f_{X+Y}(u)=\int_{-\infty}^{\infty} f_{X}(x) f_{Y}(u-x) \mathrm{d} x$
  
  • $=\int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{x^{2}}{2}} \cdot \frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{(u-x)^{2}}{2}} \mathrm{d} x$
  • $=\frac{1}{2 \pi} \mathrm{e}^{-\frac{u^{2}}{4}} \int_{-\infty}^{\infty} \mathrm{e}^{-\left(x-\frac{u}{2}\right)^{2}} \mathrm{d} x$
  • $=\frac{1}{2 \pi} \mathrm{e}^{-\frac{u^{2}}{4}} \sqrt{\pi} =\frac{1}{\sqrt{2 \pi} \cdot \sqrt{2}} \mathrm{e}^{-\frac{u^{2}}{2(\sqrt{2})^{2}}}$
• 由此可知 $X+Y\sim N(0,2)$.

---

正态随机变量的线性组合

定理： 设 rv $X_i\sim N(\mu_i,\sigma_i^2)\;(i=1,2,\ldots,n)$ 且相互独立，对任意 $a_i,b\in\mathbb{R}\;(i=1,2,\ldots,n)$,

$$\sum_{i=1}^{n}a_iX_i+b\sim N\left(\sum_{i=1}^{n}a_i\mu_i+b,\sum_{i=1}^{n}(a_i\sigma_i)^2\right)$$

• 推论： 设 $X_1,X_2,...,X_{n}$ 相互独立，则均服从 $N(\mu,\sigma^2)$，则 $\overline{X}=\frac{1}{n} \sum\limits_{i=1}^{n}X_i\sim N\left(\mu,\frac{\sigma^2}{n}\right)$.

---

离散型卷积

例：设 rv $X,Y$ 相互独立，$X\sim P(\lambda_1),Y\sim P(\lambda_2)$, 求 $Z=X+Y$ 的 pmf.

• $p_Z(z)=P\{Z=z\}=P\{X+Y=z\}$
  
  • $=\sum_{x=0}^{\infty}P\{X+Y=z|X=x\}P\{X=x\}$
  • $=\sum_{x=0}^{z} P\{Y=z-x\}P\{X=x\}$
  • $=\sum_{x=0}^{z}p_Y(z-x)p_X(x)$

---

解：

$$\begin{aligned} p_Z(z)&=\sum_{x=0}^{z}p_Y(z-x)p_X(x)\\ &=\sum_{x=0}^{z} \frac{\lambda_{2}^{z-x}}{(z-x) !} \mathrm{e}^{-\lambda_{2}} \frac{\lambda_{1}^{x}}{x !} \mathrm{e}^{-\lambda_{1}}\\ &=\mathrm{e}^{-\left(\lambda_{1}+\lambda_{2}\right)} \frac{1}{z !} \sum_{x=0}^{z} \frac{z !}{x !(z-x) !} \lambda_{1}^{z-x} \cdot \lambda_{2}^{x} \\ &=\mathrm{e}^{-\left(\lambda_{1}+\lambda_{2}\right)} \frac{\left(\lambda_{1}+\lambda_{2}\right)^{z}}{z !} \quad(z=0,1,2, \cdots) \end{aligned}$$

由此可知 $Z=X+Y\sim P(\lambda_1+\lambda_2)$.

• 两个相互独立的 Poisson rv 的和仍服从 Poisson 分布.

---

16.4.2 随机变量的差与商

定理：已知 rv $(X,Y)$ 的 pdf $f(x,y)$, 则

• $f_{X-Y}(u)=\int_{-\infty}^{\infty} f(u+v, v) \mathrm{d} v$
• $f_{X/Y}(u)=\int_{-\infty}^{\infty} f(uv, v) \cdot|v| \mathrm{d} v$

---

15.5 随机变量的最大与最小值

例： 已知 rv $X,Y$ 相互独立，pdf 均为 $f(x)$, 求 $Z_1=\max\{X,Y\}$ 和 $Z_2=\min\{X,Y\}$ 的 pdf.

• 记 $X,Y$ 的cdf 为 $F(x)$.
• $F_{Z_1}(z)=P\{\max\{X,Y\}\leq z\}=P\{X\leq z, Y\leq z\}$
  
  • $=P\{X\leq z\}P\{Y\leq z\}=[F(z)]^2$
• $f_{Z_1}(z)=\frac{\mathrm{d}}{\mathrm{d}z}F_{Z_1}(z)=\frac{\mathrm{d}}{\mathrm{d}z}[F(z)]^2=2f(z)F(z)$

---

• $F_{Z_2}(z)=P\{\min\{X,Y\}\leq z\}$
  
  • $=1-P\{\min\{X,Y\}> z\}$
  • $=1-P\{X>z\}P\{Y>z\}$
  • $=1-[1-P\{X\leq z\}][1-P\{Y\leq z\}]$
  • $=1-[1-F(z)]^2$
• $f_{Z_2}(z)=\frac{\mathrm{d}}{\mathrm{d}z}F_{Z_2}(z)$
  
  • $=\frac{\mathrm{d}}{\mathrm{d}z}\left\{1-[1-F(z)]^2\right\}=2f(z)[1-F(z)]$.

---

定理： 已知 rv $X_1,X_2,\ldots,X_n$ 相互独立，cdf 分别为 $F_{i}(x),\;i=1,2,\ldots,n$, 则

• $X_{(n)}=\max\{X_1,X_2,\ldots,X_n\}$ 的 cdf
  
  • $F_{\max}(z)=\prod_{i=1}^{n}F_i(z)$
• $X_{(1)}=\min\{X_1,X_2,\ldots,X_n\}$ 的 cdf
  
  • $F_{\min}(z)=1-\prod_{i=1}^{n}[1-F_i(z)]$

---

推论：如果 rv $X_1,X_2,\ldots,X_n$ 相互独立且同分布，cdf 和 pdf 分别为 $F(x)$ 和 pdf $f(x)$, 则

• 对 $X_{(n)}=\max\{X_1,X_2,\ldots,X_n\}$
  
  • cdf: $F_{\max}(z)=[F(z)]^n$
  • pdf: $f_{\max}(z)=n f(z)[F(z)]^{n-1}$
• 对 $X_{(1)}=\min\{X_1,X_2,\ldots,X_n\}$
  
  • cdf: $F_{\min}(z)=1-[1-F(z)]^n$
  • pdf: $f_{\min}(z)=n f(z)[1-F(z)]^{n-1}$

---

例：指数分布随机变量的最小值的分布

设 $X,Y$ 相互独立，且 $X\sim\mathrm{Exp}(\alpha)$, $Y\sim\mathrm{Exp}(\beta)$, 证明 $Z=\min\{X,Y\}\sim\mathrm{Exp}(\alpha+\beta)$.

• 相互独立的指数随机变量的最小值仍服从指数分布.

---

证：

$$\begin{aligned} F_{\min }(z)&=1-\left[1-F_{X}(z)\right]\left[1-F_{Y}(z)\right]\\ &=\left\{\begin{array}{cc} 1-\mathrm{e}^{-\alpha z} \cdot \mathrm{e}^{-\beta z}& z>0 \\ 0 & z \leq 0\end{array}\right.\\ &=\left\{\begin{array}{cc} 1-\mathrm{e}^{-(\alpha+\beta) z} &z>0 \\ 0 & z \leq 0\end{array}\right. \end{aligned}$$

故 $f_{Z}(z)=\left\{\begin{array}{cc}(\alpha+\beta) \mathrm{e}^{-(\alpha+\beta) z} &z>0 \\ 0 & z \leq 0\end{array}\right.$, 由此可知 $Z\sim\mathrm{Exp}(\alpha+\beta)$.

---

小结

• 重点：
  
  • 利用卷积公式求随机变量和的分布
  • 最大值和最小值的分布
• 理解以上公式的推导方法
• 了解 Jacobi 行列式的性质

---

A mathematician is a machine for turning coffee into theorems.
--Paul Erdös

---

补充例题

例： 已知 rv $R_1,R_2$ 独立同分布，pdf 为

$$f(x)=\left\{\begin{array}{cc} \frac{10-x}{50}& 0 \leq x \leq 10 \\ 0 &\text {其他} \end{array}\right.$$

求 $R=R_1+R_2$ 的 pdf.

---

解： 由卷积公式

$$f_{R}(z)=\int_{-\infty}^{\infty} f(x) f(z-x) \mathrm{d} x$$

被积函数取值非零的区域为

$$\left\{\begin{array}{l}{0<x<10} \\ {0<z-x<10}\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}{0<x<10} \\ {z-10<x<z}\end{array}\right.$$

---

因此,

$$\begin{aligned} f_{R}(z)&=\left\{\begin{array}{cc}{\int_{0}^{z} f(x) f(z-x) \mathrm{d} x,} & {0 \leq z<10} \\ {\int_{z-10}^{10} f(x) f(z-x) \mathrm{d} x,} & {10 \leq z \leq 20} \\ {0,} & {\text {其他}}\end{array}\right.\\ &=\left\{\begin{array}{cc} \frac{600 z-60 z^{2}+z^{3}}{15000},&0 \leq z<10 \\ \frac{(20-z)^{3}}{15000}, &10 \leq z<20 \\ {0,} & {\text {其他}}\end{array}\right. \end{aligned}$$

---

例： 设 $X,Y$ 相互独立，均服从 $b(n,p)$，证明：$X+Y\sim b(2n,p)$.

• 提示：$\sum\limits_{k=0}^{i}C_n^kC_m^{i-k}=C_{m+n}^i$