@blueband21c
2023-04-24T13:12:04.000000Z
字数 5470
阅读 5395
第九讲 连续型随机变量及其概率分布
概率论与数理统计 讲义 NUDT 2023SP
9.1 连续型随机变量
- 连续型随机变量 (Continuous rv)
- 值域为 上的某个区间
- 例:
- 随机选择不同的位置测量湖水的深度,记为 ,
- 设 为该湖泊的最大深度,
- 则 .
从直方图到密度曲线
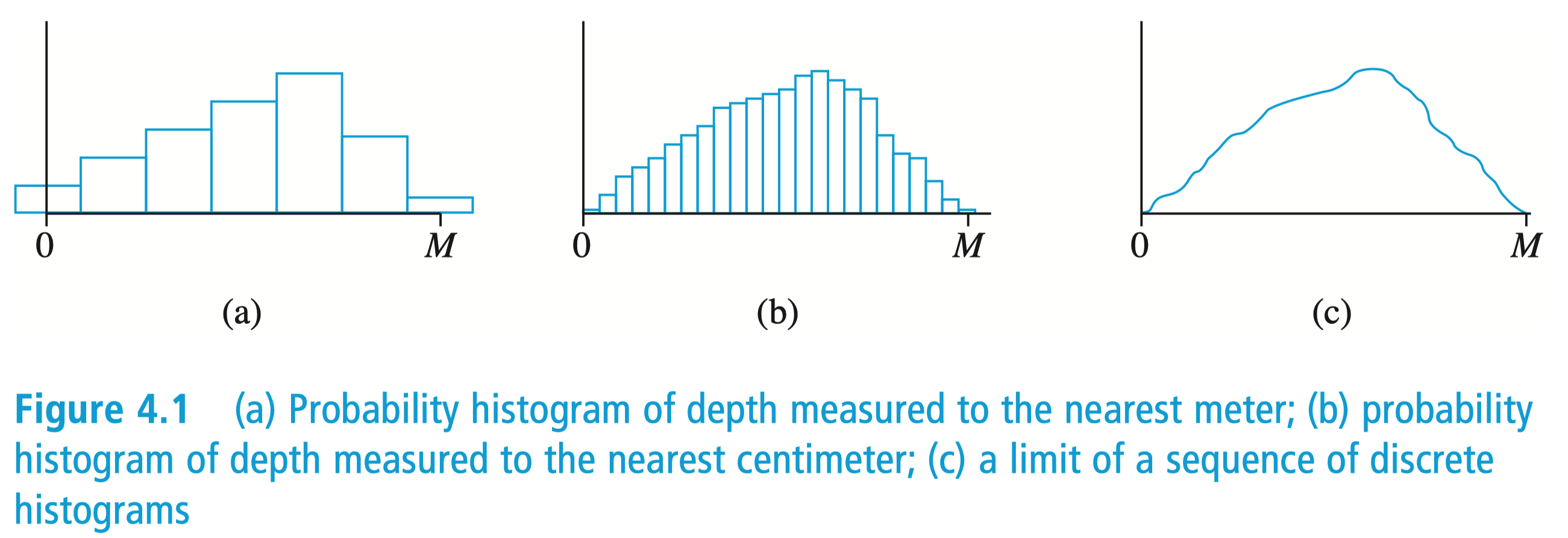
- 按照不同的粒度(变化幅度)对不同深度值出现的频率进行统计,随着粒度的不断细化,顶部曲线趋于平滑
概率密度函数
随机变量 取值于 ,如果存在函数 满足:对任意 ,总有
则称 为连续型随机变量, 是 的概率密度函数 (probability density function,缩写:pdf ).
- pdf 的本征特性: (1) 对任意 , ; (2) .
例:车辆通过的时间间隔
设 rv 为高速公路上任意相邻两台车通过同一个计时点的时间间隔,已知 的 pdf 为:
- 则两辆相邻的汽车行驶间隔不超过 5 秒的概率
例:均匀取值的连续型随机变量
rv 表示某个从 到 等可能取值的角度值,其 pdf 可表示为
- 的取值介于 和 之间的概率
均匀分布
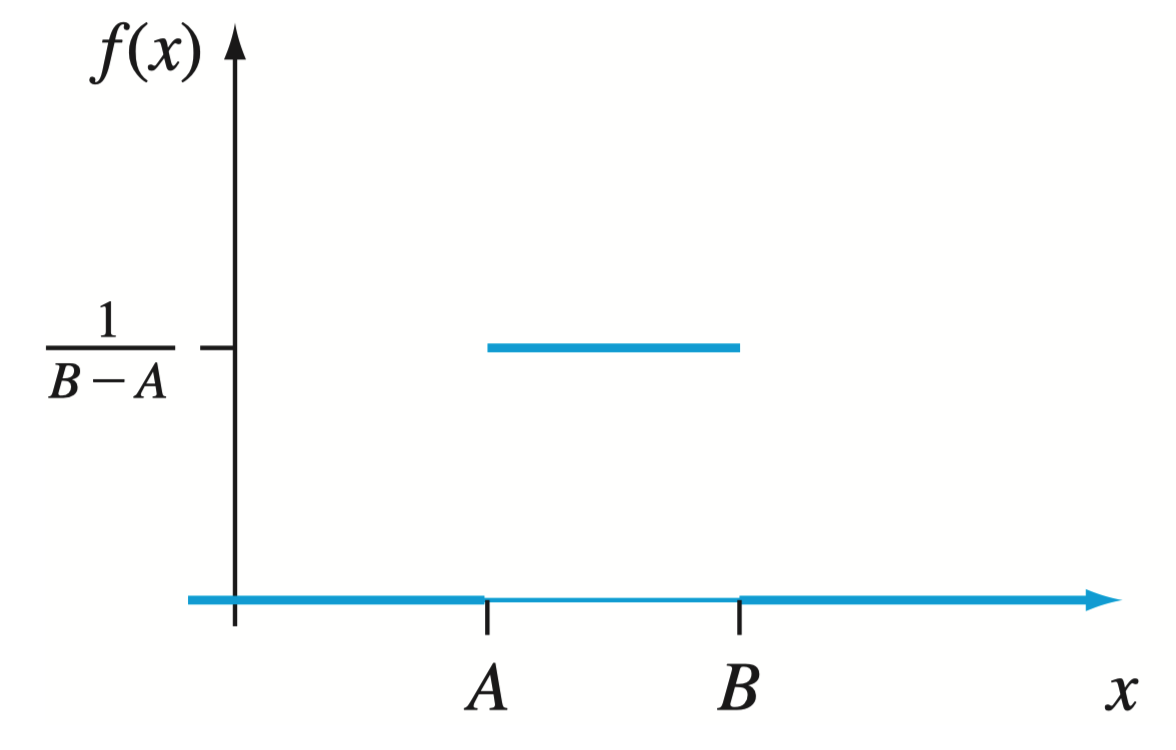
rv 服从区间 上的均匀分布(uniform distribution),是指其 pdf 为
- 记为:
连续型 rv 的性质
定理:给定连续型 rv 和任意常数
- 推论:给定连续型 rv 和任意的
-
密度函数曲线与概率
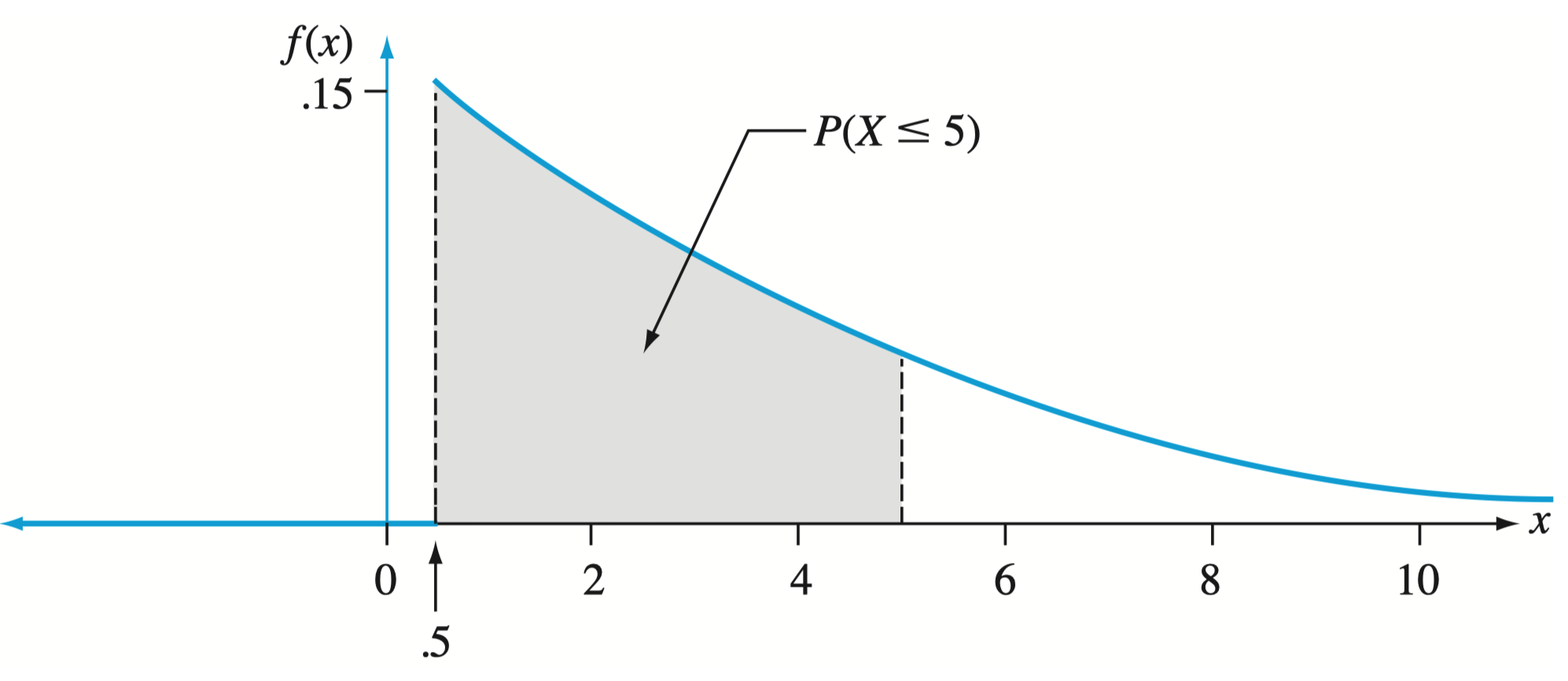
- pdf 的取值不是概率,但可以用来导出概率值.
- 在给定区间范围内,pdf 曲线与横轴所夹的面积即为该区间对应事件的概率.
连续型 rv 的概率分布函数
对连续型 rv ,其概率分布函数(或累积分布函数,缩写:cdf)为
其中 为 的 pdf.
pdf 与 cdf
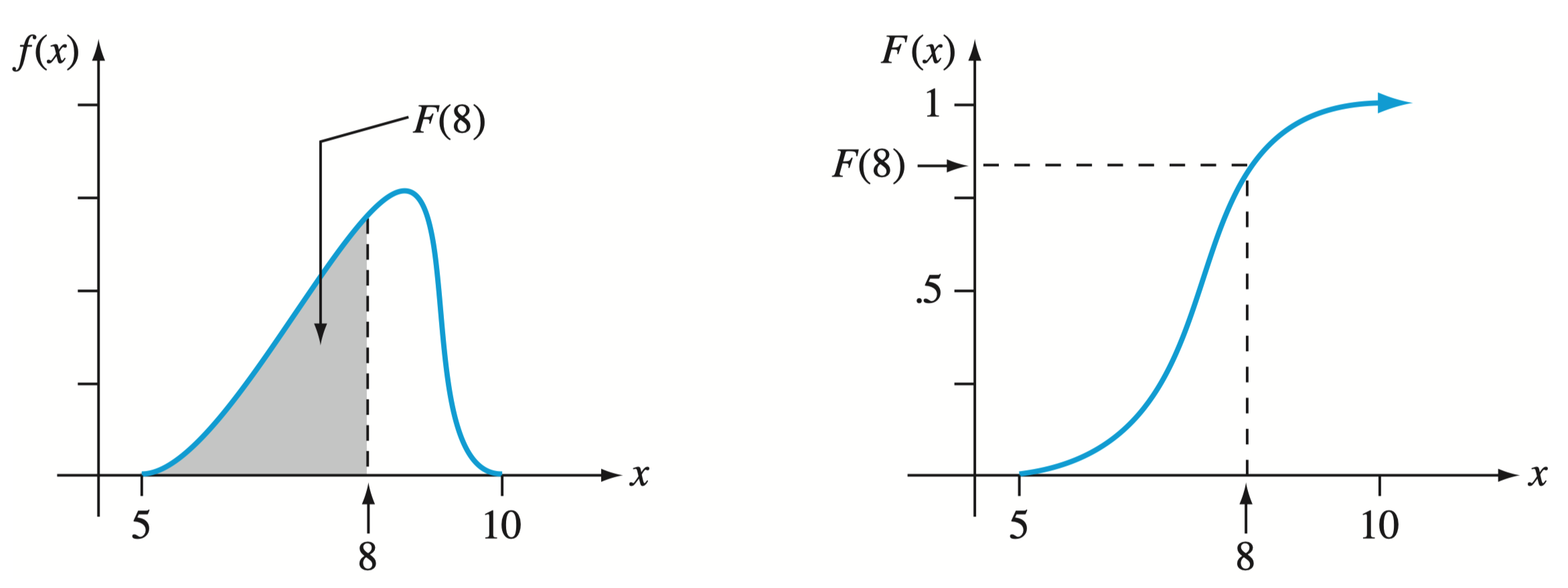
例:设某桥梁的动态载荷 的 pdf 为
其中 为常数, 求 的 cdf.
解:由 pdf 的性质,
故 . 对任意
故 的 cdf 为
例:假设某电源系统的输出电压为 ,且 大于 的概率与 成反比, 求 的 pdf.
- 设
- 其中 为常数.
- 由 , 可得 .
- 于是 的 cdf
- 进而 的 pdf
均匀分布的 pdf 与 cdf
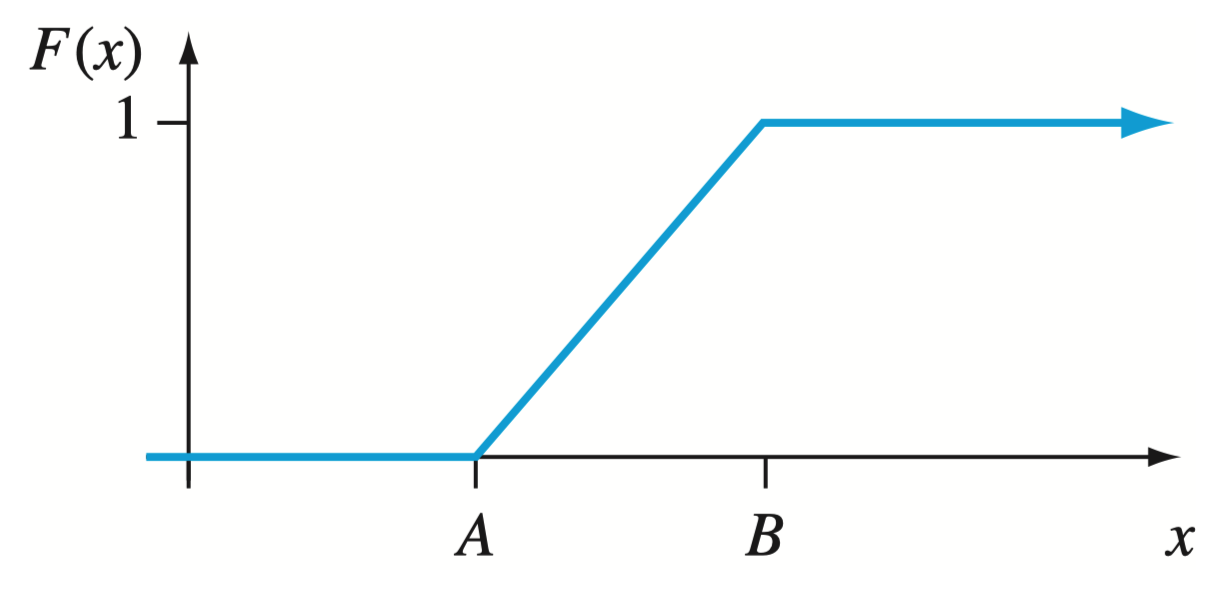
9.2 连续型分布的分位点
设 . 对连续型 rv ,若 , 则称 是 对应的概率分布的 分位点
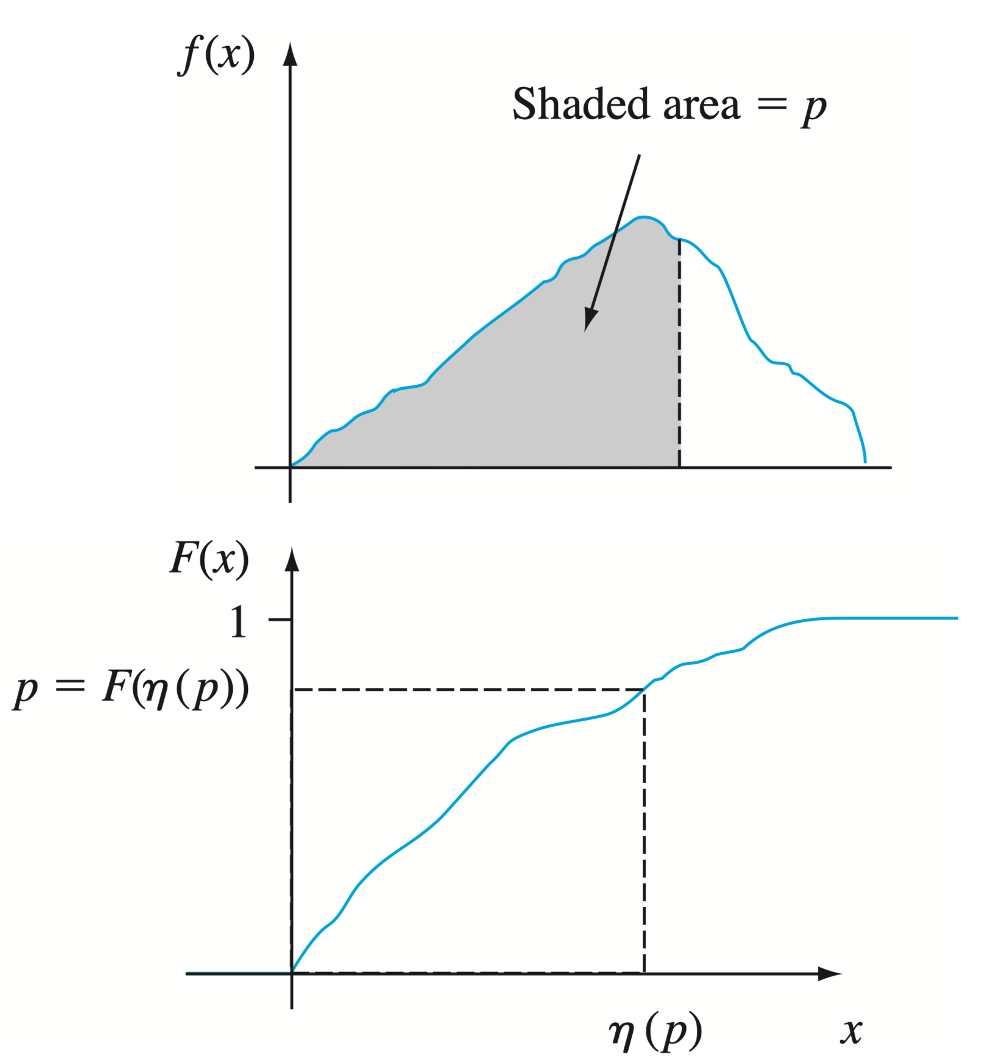
例: 连续型 rv 的 pdf 为
求其分布的 分位点.
- 分位点 通常也称为该分布的 中位数 (median).
解:对 , 的 cdf
进而
令 , 可得
解得 .
9.3 连续型随机变量的期望值
设连续型 rv 的 pdf 为 ,则其 期望 或 均值 可定义为
- 当 发散时,称 不存在.
- 设 服从 Cauchy 分布,pdf ,不难验证 不存在.
例:设连续型 rv 的 pdf 为
求 .
连续型随机变量的函数的期望
定理:设连续型 rv 的 pdf 为 , 是关于 的连续函数,则
- 如果 是离散型 rv,pmf 为 ,则
例: 连续型 rv 的 pdf 为
求 .
解:
数学期望的线性性
推论: 对 rv (无论 为离散型还是连续型)
- 任取 ,
- .
- 任取 ,
- .
- 求期望的运算可以和线性运算(加法和数乘)交换次序
9.4 连续型随机变量的方差
连续型 rv 的 pdf 为 且其期望存在,则
称为 的方差
- 称为 的标准差.
方差的性质
定理: 对任意(离散或连续型)随机变量
- 对任意 ,
- 对任意 ,
均匀分布的方差
设
小结
- 连续型 rv 的概率分布
- pdf 和 cdf
- 期望和方差
- 均匀分布 的 pdf、cdf、期望和方差
- 与离散型 rv 的异同
- cdf 的定义相同
- pdf 不是概率,而只是 cdf 的变化率
- pmf 可视为对 cdf 的差分
‘Obvious’ is the most dangerous word in mathematics.
-- Eric Temple Bell
熵与信息论
给定概率空间 ,事件的熵 (Entropy) 是形如
的函数. 满足
- 如果 ,则 .
- 如果 相互独立,则 .
- 对任意 , .
随机变量的熵
离散型随机变量 的分布律为 ,则 的熵定义为
- 若 是密度函数为 的连续型随机变量,则其熵定义为
最大熵优化
- 连续随机变量的种类非常丰富,对其一一做研究显然不很现实.
- 一般来说,需要从中选择代表性较强,应用较为广泛的典型例子.
- 在同等条件下,具有最大熵性质的连续随机变量包含的信息量最多.
- 因此,最大熵准则(maximum entropy principle)就成为挑选典型的随机变量的一个重要出发点.
具有最大熵的连续型随机变量
问题: 给定连续型随机变量 的取值区间 ,以及某些关于其数字特征的约束条件,求 的分布,使其熵 取到最大值.[1]
- ,且 ,
- 且
- .
