@blueband21c
2023-04-24T12:41:29.000000Z
字数 8250
阅读 4974
第十九讲 大数定律与中心极限定理
概率论与数理统计 讲义 NUDT 2023SP
概率论中的极限定理
- 大数定律(the Law of Large Numbers)
- 随机变量序列的前部分项的算术平均值在某种条件下收敛到这些项的均值的算术平均值
- 中心极限定理(the Central Limit Theorem)
- 在一定条件下,大量随机变量的和的分布趋近于正态分布
19.1 大数定律
- 频率的稳定性:在大量重复试验中,随机事件 发生的频率随着试验次数的增加而趋于稳定.
- Bernoulli 大数定律:二项试验的成功频率
- Chebyshev 大数定律:两两不相关的随机变量列
- Khinchin 大数定律:独立同分布的随机变量列
依概率收敛
设 是一个随机变量序列, 是一个随机变量,若对任意 ,总有
则称序列 依概率收敛到 . 记为:
- 等价的形式:
一个依概率收敛的实例
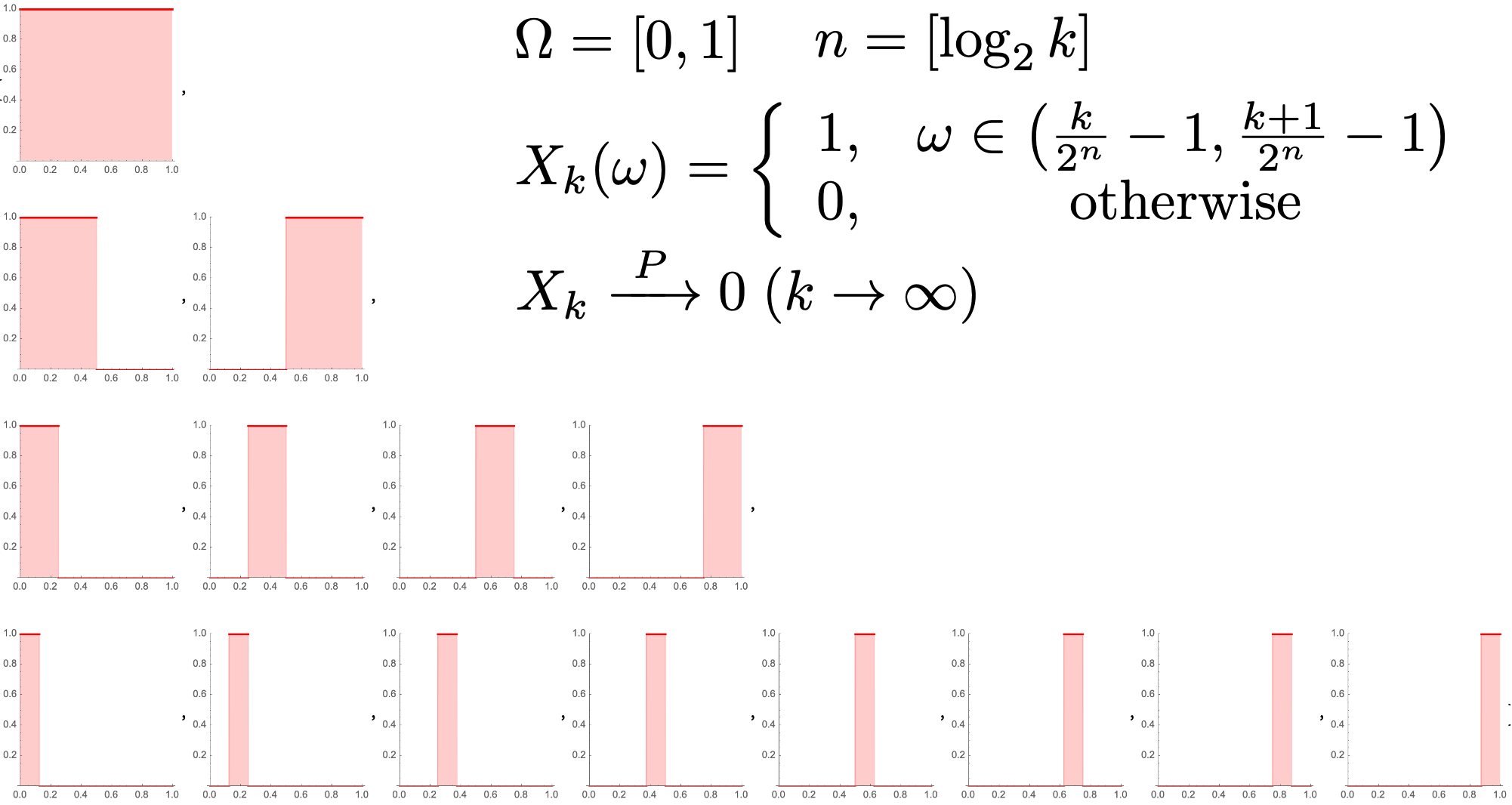
- 随着 的增大,随机变量 与随机变量 存在差异的部分越来越少.
- 但是对于任意的 ,不难发现 都不收敛到 .
- 依概率收敛本质上是一种函数列的整体收敛.
依概率收敛的性质
设 , ,则
- .
- .
- 若 ,,则 .
- 若函数 在 处连续,则 .
Bernoulli 大数定理
设 是 重 Bernoulli 试验(二项试验)中的成功次数,若每次试验中成功的概率为 ,则
- 只要重复的次数足够多, 与 的偏差较大的情况几乎不会发生
Chebyshev 大数定理
设 为两两不相关的随机变量列,且每个每个随机变量的方差有共同的上界,则 服从大数定律.
- 所谓服从大数定律,是指
Chebyshev 不等式
设随机变量 的期望和方差均存在,则对任意 ,
再看 3-sigma 原理
- 设 , .
- 由 Chebyshev 不等式,
- The upper bound in Chebyshev inequality is sharp(精确的), in the sense that it cannot be made any smaller and still hold for all distributions.
Khinchin 大数定理(弱大数定理)
定理: 设 是独立同分布(independent and identical,缩写:iid)的随机变量序列,且数学期望存在,则 服从大数定律.
- 在方差存在的条件下,以上定理是 Chebyshev 大数定理的直接推论.
- 推论: 设 是独立同分布的随机变量列,且 阶原点矩存在,则 服从大数定律.
在方差存在的条件下证明弱大数定理
- 记
- 由夹逼准则,
利用大数定律计算积分
问题: 给定函数 ,求 的近似值.
- 考虑独立同分布的随机变量
例 求积分 的近似值.
- 结果 .

19.2 中心极限定理
- 在实际应用中,许多随机变量是由大量相互独立的随机因素叠加产生的.
- 如果其中每个因素在总的影响中所起的作用都是微小的
- 即:没有任何一个因素的影响占据绝对主导的地位
- 则往往这样综合得到的随机变量近似地服从正态分布
Lindeberg-Levy 中心极限定理
定理 设随机变量 独立同分布,且存在期望 和方差 ,则标准化随机变量 的分布函数 对任意 满足
记为:
例:电压噪声的叠加
一个高压变电器同时可接收到 20 个噪声电压,已知每个噪声源互不干扰,且服从 10 伏以内的均匀分布,求总的噪声电压不超过 105 伏的概率.
- 记每个噪声电压为
- 且相互独立,期望和方差都存在
- 满足独立同分布的中心极限定理的条件
解:
- 相互独立
- ,
- 记 ,由中心极限定理
-
De Moivre-Laplace 中心极限定理
定理:设随机变量 ,则
- 记 ,其中 独立同分布
- 记 为 90000 次中纵摇角大于 的次数
-
- 思考:本例可以使用 Poisson 分布来近似二项分布进行计算吗?
例:运气的重要性
大学英语四级考试,设有 85 道选择题,每题 4 个候选答案,只有一个正确. 要通过考试,必须答对 51 题以上. 求完全靠运气能通过考试的概率.
解:
- 定义 .
- 相互独立,且 ,.
-
例:图书馆的座位
- 某大学图书馆共有 1000 个座位.
- 已知该大学有 10000 名学生,同一时刻,每个学生去图书馆的概率为 0.1.
- 问:现有座位能否以 的概率满足需要?
- 如果不能,需要增加多少座位?
分析:
- 设 为去图书馆的学生人数,则 .
-
- 这说明现有的座位数不足以满足要求.
- 设还需要增加 个座位,即
- 也即
- 从而可知 ,进而 .
- 结论:再增加 50 个座位,即可满足要求.
Lyapunov 中心极限定理
定理三:设随机变量 相互独立,且分别存在期望 和方差 ,记 . 若存在正数 ,满足
则
例:考试通过的概率
某次考试共有考题 99 个,按从易到难的顺序排列,并假设某学生答对第 题的概率为 ,. 如果每道题是否答对是相互独立的,且至少答对 60 题才能通过考试,求该学生通过考试的概率.
解:
- 定义
- 相互独立
- ,
- 时,
- 取
-
- 由 Lyapunov 定理
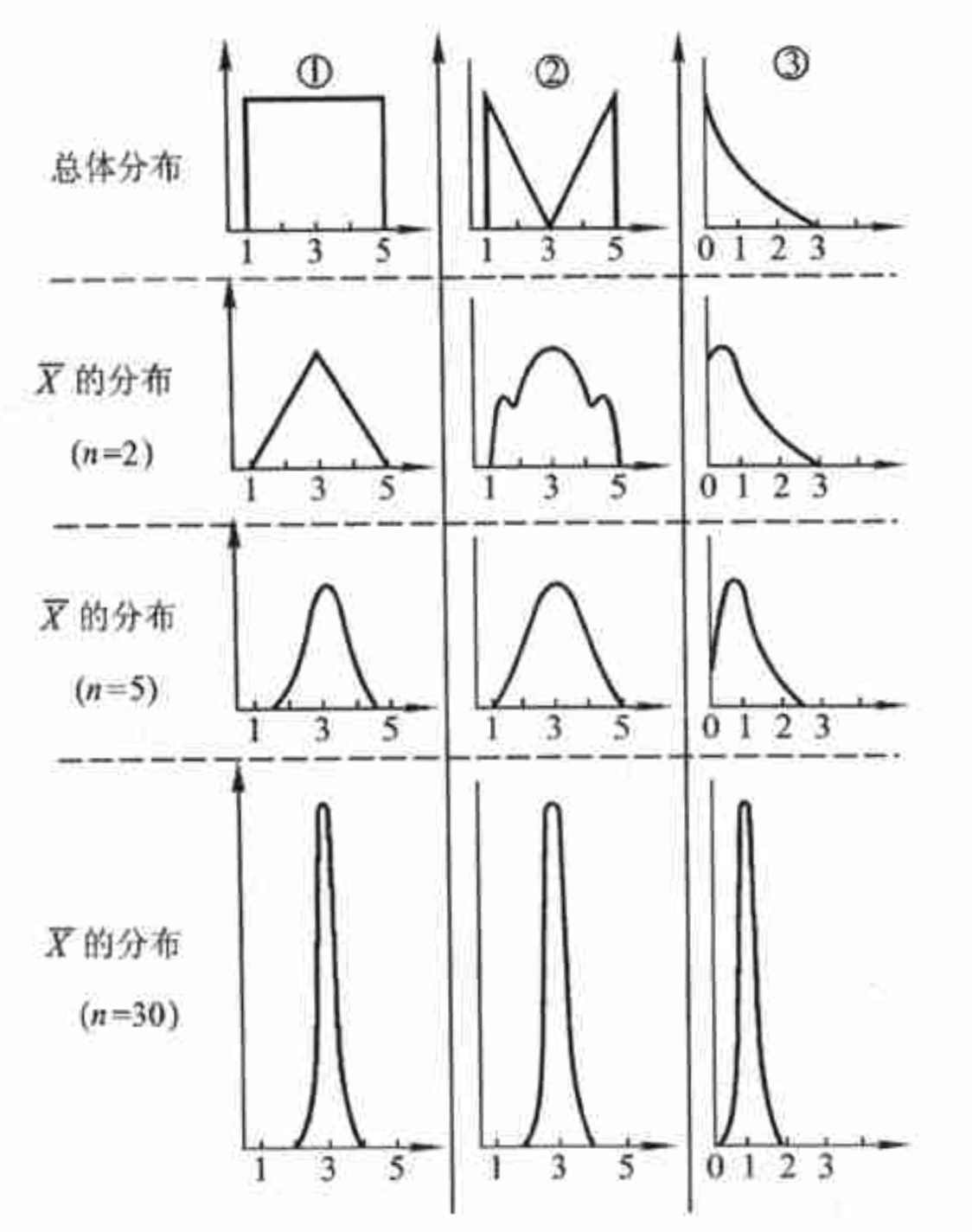
中心极限定理的意义
- Lyapunov 定理说明,无论各个随机变量 服从什么分布,只要满足定理的条件,则当 充分大时,其和 就近似服从正态分布
例
-
- 近似服从
- 的密度函数为
- 近似服从
-
- 近似服从
小结
- 正确理解大数定律与中心极限定理的含义
- 理解依概率收敛的含义
- 重点:利用中心极限定理估算概率
- 独立同分布的中心极限定理
- De Moivre-Laplace 定理
- 了解 Chebyshev 不等式
All sciences are vain and full of errors that are not born of Experience, the mother of all Knowledge.
--Leonardo da Vinci
