第十一讲 经济学中的数学模型

数学建模 讲义 NUDT 2023SP

---

---

11.1 实物交换模型

• 实物交换的原则：互通有无，等价交换
• 决定价格的依据：物品的稀缺性
  
  • 物以稀为贵
• 在交易者眼中，自己越是缺少的物资（产品、信息）具有越高的价值，从而愿意为之付出更高的价格

---

等效用曲线

• 甲乙双方进行物品 X，Y 的交易
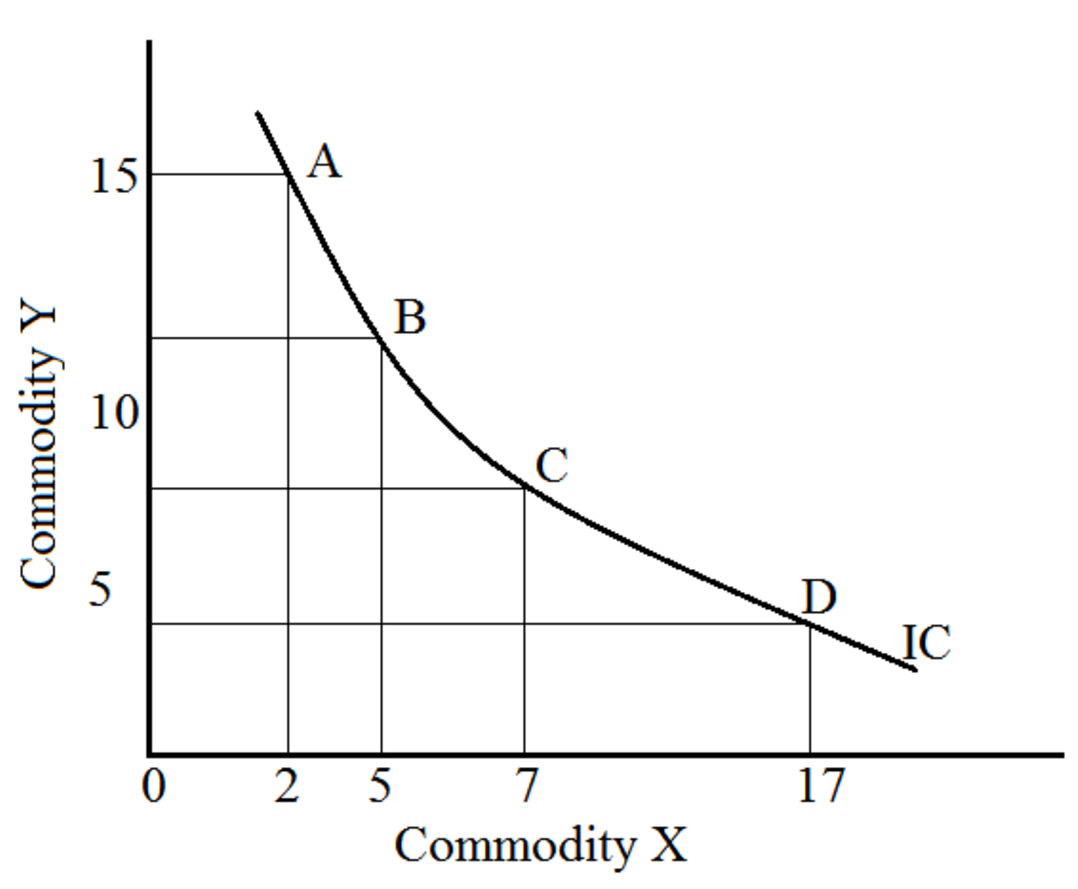
• 甲方的等效用曲线 (无差异曲线，Indifference Curve) 反映了甲对 X, Y 的偏爱程度，对应于消费者获得同样的效用时的不同消费组合
  
  • $U(x,y)=C$，其中 $x,y$ 分别为甲拥有的 X，Y 的数量

---

效用

• 效用（Utility）是微观经济学中最常用的概念之一，一般是指消费者对各种财货（服务）消费的相对满意度
  
  • 对于投资而言，是指投资者从不同的投资组合中获得的满意度
• 基于理性选择的经济学理论通常认为消费者会尽可能最大化其效用

---

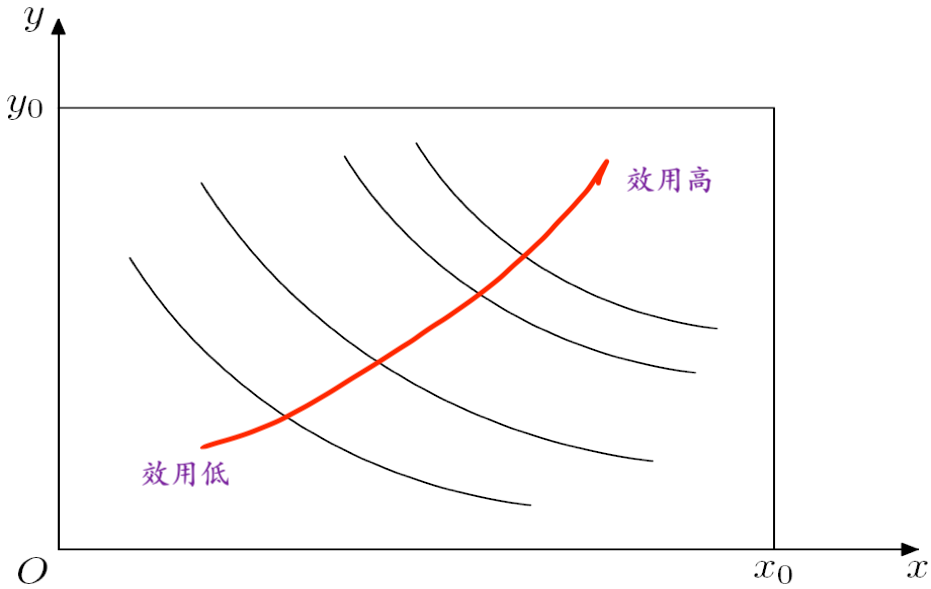
等效用曲线的特征

$$U(x,y)=C.$$

• 单调递减：物品 X 的增加必须以物品 Y 的减少为代价
• 互不相交：对同一交换方案，不应有不同的满意度值
• 下凸：$-\Delta y/\Delta x$ 关于 $x$ 递减（或 $y''(x)>0$）
  
  • 即：随着甲手中 X 数量的增加，付出等量的 X 能换回的 Y 的数量越来越少

---

双方满意的交换方案

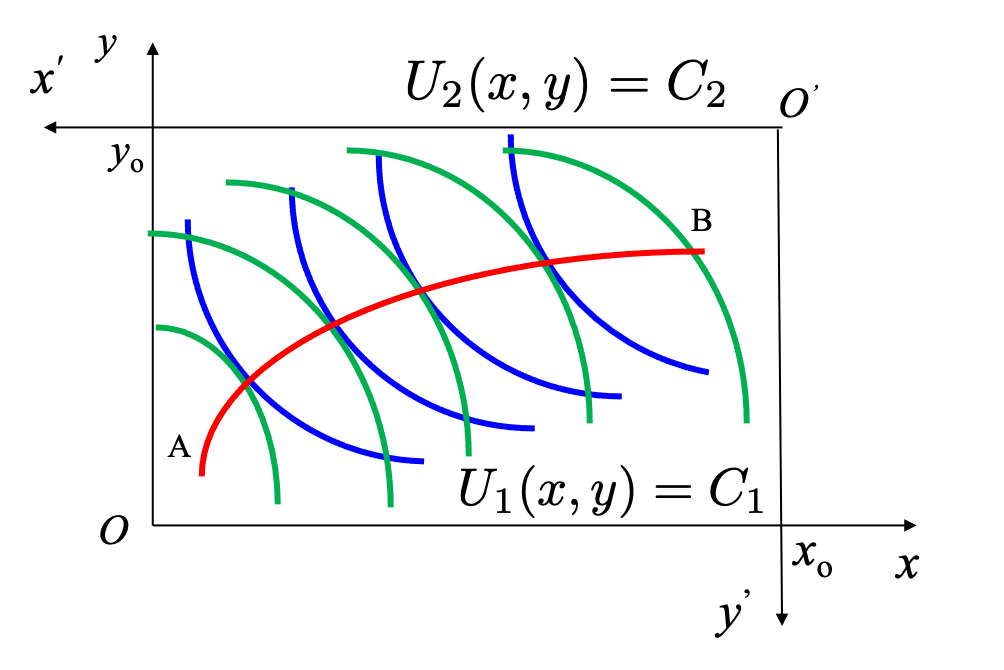
• 记甲乙双方的无差别曲线分别为 $U_1(x,y)=C_1$ 和 $U_2(x,y)=C_2$.
  
  • $x_0,y_0$ 分别表示甲乙两方拥有的 X、Y 的总量.
• 双方都满意的交换方案一定落在曲线 AB 上，且此时意味着 Pareto 最优.

---

边际效用

• 在消费的过程中，每个人总是以效用最大化为目标.
• 设某人关于商品 X、Y 的效用函数为 $U(x,y)$
  
  • $x,y$ 表示该人拥有的 X、Y 的数量.
• 则该人消费最后一单位商品所获得的效用（边际效用，Marginal Utility）分别为 $MU_x=\dfrac{\Delta U}{\Delta x}$ 和 $MU_y=\dfrac{\Delta U}{\Delta y}$
  
  • 对于连续可微的函数 $U$，可记 $MU_x=\dfrac{\partial U}{\partial x}$ 和 $MU_y=\dfrac{\partial U}{\partial y}$

---

例：面包还是苹果

• 一个面包价值 2 元，一个苹果价值 1 元.
• 张三已有 2 个面包与 2 个苹果.

• 假设这时面包的边际效用为 3 个单位，苹果的边际效用是 1 个单位，张三接下来会购买哪一种商品？

• 分析： $3/2=1.5>1/1=1$, 即张三接下来花 $1$ 元钱购买苹果可带来 $1$ 个单位的效用增量，而购买面包可带来 $1.5$ 个单位的效用增量，所以张三会购买面包.

---

例：蚂蚁的选择

生物学家 Adam Kay 研究了蚂蚁的觅食选择. 实验中，每天给蚁群一定量的 $6\%$ 的酪蛋白（富含蛋白质）溶液，观察是否会影响它们在蛋白质食源和糖类食源之间的选择. 控制组的蚁群待遇一样，只是用清水代替了酪蛋白溶液.

$$\boxed{ \begin{array}{c|c|c} \text{食源} & \text{控制组：只提供水} & \text{实验组：提供酪蛋白}\\\hline \text{糖类食源} & 20\% & 48\% \\ \text{混合食源} & 48\% & 37\% \\ \text{蛋白食源} & 32\% & 15\% \end{array} }$$

• 实验显示：当食物中有了更多的蛋白质供应时，蚁群对蛋白食品的偏好降低了.

---

11.2 最佳消费选择模型

• 问题： 在资金一定的条件下，如何确定最佳的商品消费组合，以达到总效用的最大化？
• 边际效用递减律：商品的边际效用随着消费量的增加而下降.
• 假设只考虑两种商品 X, Y (其数量分别表示为 $x$, $y$，价格分别为 $P_x,P_y$)，总资金为 $n$
• 最后一元钱的边际效用分别为：$\dfrac{MU_x}{P_x}$，$\dfrac{MU_y}{P_y}$

---

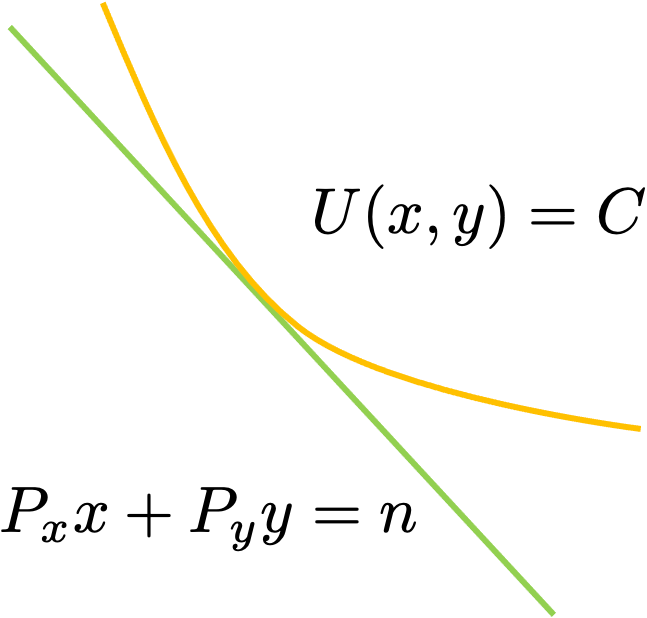
最佳消费选择原理

$$\bbox[yellow]{\dfrac{MU_x}{P_x}=\dfrac{MU_y}{P_y}}$$

• 等效用曲线与等支出曲线相切时，上式成立.
  
  • 在切点处：$\dfrac{\mathrm{d}y}{\mathrm{d}x}=-\dfrac{U'_x}{U'_y}=-\dfrac{P_x}{P_y}$.
• 即：购买两类商品的边际效用相等.

---

边际分析

• 边际收入：增加单位产量（$Q$）时收入（$R$）的增加量，$MR=\dfrac{\Delta R}{\Delta Q}$
  
  • 若 $R$ 可微，记为：$MR= \dfrac{\mathrm{d}R}{\mathrm{d}Q}$
• 边际成本：增加单位产量时导致的费用（$C$）增加量
  
  • $MC=\dfrac{\Delta C}{\Delta Q}$ 或 $MC= \dfrac{\mathrm{d}C}{\mathrm{d}Q}$
• 在市场竞争条件下，边际收入是产量的递减函数，而边际成本是产量的递增函数（销售难度越来越大）.
• 利润最大化原理：当边际收入等于边际成本时，达到最优产量，此时边际利润为零.

---

例：报纸的采购与销售

• 报纸每份批发价 $b$，零售价 $a$，退回价 $c$.
• 显然应有 $a>b>c$.
• 已知每天报纸需求为 $r$ 份的概率是 $p(r)$.
• 问报刊亭每天应购入多少份该报纸？

---

分析

• 设每天购进 $n$ 份，当需求为 $r$ 份时的获利为
  
  • $G(n,r)=\begin{cases} (a-b)r-(b-c)(n-r), & r\leq n\\ (a-b)n, & r>n \end{cases}$
• 当 $n$ 很大时，可将 $r$ 视为连续型随机变量.
• $E(G)=\int_0^{\infty}G(n,r)p(r)\mathrm{d}r$
  
  • $=\int_0^n[(a-b)r-(b-c)(n-r)]p(r)\mathrm{d}r+\int_n^{\infty}(a-b)np(r)\mathrm{d}r$

---

期望利润最大的条件

• $\dfrac{\mathrm{d}E(G)}{\mathrm{d}n}=-\int_0^n(b-c)p(r)\mathrm{d}r+\int_n^{\infty}(a-b)p(r)\mathrm{d}r$.
• 令 $\dfrac{\mathrm{d}E(G)}{\mathrm{d}n}=0$，可得
  
  • $(b-c)\int_0^np(r)\mathrm{d}r=(a-b)\int_n^{\infty}p(r)\mathrm{d}r$
  • 也即：$(b-c)P\{r<n\}=(a-b)P\{r\geq n\}$

---

结果的解释

$$(b-c)P\{r<n\}=(a-b)P\{r\geq n\}$$

• 收入：$R(n,r)=\begin{cases} (a-b)r, & r\leq n\\ (a-b)n, & r>n \end{cases}$
• 退回成本：$C(n,r)\begin{cases} (b-c)(n-r), & r\leq n\\ 0, & r>n \end{cases}$
• 显然：$G(n,r)=R(n,r)-C(n,r)$，进而 $E(G)=E(R)-E(C)$.

---

$$\dfrac{\mathrm{d}E(G)}{\mathrm{d}n}=0\quad\Leftrightarrow \quad \dfrac{\mathrm{d}E(R)}{\mathrm{d}n}=\dfrac{\mathrm{d}E(C)}{\mathrm{d}n}$$

• $E(R)=P\{r\geq n\}(a-b)$，$E(C)=P\{r<n\}(b-c)$.
• 故期望（平均）利润最大化的条件可理解为：平均边际收入等于平均边际成本.

---

11.3 价格弹性模型

• 边际（$\mathrm{d}y/\mathrm{d}x$：函数改变量（$\Delta y$）与自变量改变量（$\Delta x$）的比值的极限 （$\Delta x\to 0$ 时）
• 弹性：函数相对改变量与自变量相对改变量的比值的极限，即：
  
  • $\varepsilon_{yx}=\lim\limits_{\Delta x\to 0}\dfrac{\Delta y/y}{\Delta x/x}=y'(x)\dfrac{x}{y}$
• 弹性是无量纲的，反映的是自变量变化时函数的相对变化量的大小（例如：价格变动 $1\%$ 时供应量变化的百分比）.
• 若 $|\varepsilon_{yx}|=1$，称为单位弹性；$|\varepsilon_{yx}|<1$，称为低弹性；否则称为高弹性.

---

价格弹性

• 供给价格弹性：$\varepsilon_{Q_sP}=\dfrac{\mathrm{d}Q_s}{\mathrm{d}P}\cdot\dfrac{P}{Q_s}$
• 需求价格弹性：$\varepsilon_{Q_dP}=-\dfrac{\mathrm{d}Q_d}{\mathrm{d}P}\cdot\dfrac{P}{Q_d}$
  
  • $Q_s$：商品的供给函数
  • $Q_d$：商品的需求函数
  • $P$：商品价格

---

边际收益

• 收益 $R=Q_dP$
• 边际收益 $MR=\dfrac{\mathrm{d}R}{\mathrm{d}Q_d}=P+Q_dP'=P\left(1+\dfrac{Q_d/P}{\mathrm{d}Q_d/\mathrm{d}P}\right)=P\left(1-\dfrac{1}{\varepsilon_{Q_dP}}\right)$
• 当需求价格弹性大于 1 时，边际收益 $MR>0$.
• 2005 年研究生数学建模竞赛 C 题：出租车价格调整.
  
  • 直观上容易知道，相对低的价格会刺激需求，但价格定在多少合适呢？这时需求价格弹性就起到了关键作用.

---

Engel 函数

• 设消费者收入水平为 $x$，Engel 函数 定义为 $Q_d = Q_d(x)$
• Engel 边际：$\dfrac{\mathrm{d}Q_d}{\mathrm{d}x}$
  
  • $\dfrac{\mathrm{d}Q_d}{\mathrm{d}x}>0$：需求量随着收入的增加而增加，意味着商品为正常商品
  • $\dfrac{\mathrm{d}Q_d}{\mathrm{d}x}<0$：收入的增加，需求量反而减少，意味着商品为低质商品（Giffen 商品，Giffen Goods）

---

应用举例

• 假设某种商品的 Engel 函数为 $Q_d(x)=a\exp\dfrac{b}{x}\;(a>0)$
• 边际函数 $Q'_d(x)=-\dfrac{ab}{x^2}\exp\dfrac{b}{x}$
  
  • $b<0$ 时，该商品为正常商品，否则为 Giffen 商品.
• 弹性 $\varepsilon_{Q_dx}=Q'_d\dfrac{x}{Q_d}=-\dfrac{b}{x}$
  
  • $b<0$ 时，也即该商品为正常商品时，需求量对于消费者收入的弹性随着 $x$ 的增加而减少.
  • 消费者收入水平越高，收入的改变量对该种商品的需求量的影响程度就越小，此类商品可以称之为 高端必需品（例：手机）

---

11.4 综合案例：三城镇的污水处理方案

• 沿河有三个城镇（依次相距 20 和 38 km），污水需处理后才能排入河中，三镇或者单独建厂，或者联合建厂，用管道将污水集中处理.
• $Q$ 表示污水量（t/s），$L$ 表示管道长度（km）.
• 按照经验公式，污水处理厂的建厂费用为 $C_T=730\,Q^{0.712}$，铺设管道的费用为 $C_P=6.6\,Q^{0.51}L$.
• 已知三镇的污水量分别为 $Q_1=5$t, $Q_2=3$t, $Q_3=5$t. 试从节约总投资的角度为三镇制定污水处理方案.

---

候选方案

1. 三镇各自建厂，总投资 $S(1)=6188.2$ 万元
2. 1、2 合作，总投资 $S(2)=5735.9$ 万元
3. 2、3 合作，总投资 $S(3)=5943.9$ 万元
4. 1、3 合作，总投资 $S(4)=6227$ 万元

5. 1、2、3 合作，总投资 $S(5)=5308.5$ 万元

   • 显然应该选择 方案 5，问题是费用如何分摊？

---

合作分配问题

• 例（n 人合作分配问题）
  
  • 甲、乙、丙三人经商，若单干，每人仅能获利 1 元；
  • 甲、乙合作可获利 7 元；甲、丙合作可获利 5 元；乙、丙合作可获利 4 元；三人合作可获利 10 元.
  • 现选择三人合作，问应如何分配 10 元的收入.
• 分配原则：按照各人对合作的贡献来进行分配.

---

合作中的贡献

• 某人对于某一合作的贡献定义为：有该人参加合作时的收入与无该人合作时的收入之差.
• 以甲为例，计算其贡献：
  
  • 甲：$1-0=1$ 元；
  • 甲乙：$7-1=6$ 元；
  • 甲丙：$5-1=4$ 元；
  • 甲乙丙：$10-4=6$ 元.
• 甲应分得的收入是这四个值的加权平均值.

---

多人合作模型

一般的 $n$ 人合作模型如下：

• $I = \{1,2, \ldots ,n\}$：合作各方
• $v$：合作获利函数，也称为 特征函数
  
  • 例：$v(\mbox{甲})=v(\mbox{乙})=v(\mbox{丙})=1$, $v(\mbox{甲乙})=7$, $v(\mbox{甲丙})=5$, $v(\mbox{乙丙})=4$, $v(\mbox{甲乙丙})=10$.
• $\varphi_i(v)$：第 $i$ 人的合作获利分配值，$i=1,2,\ldots,n$
• $\Phi(v) = (\varphi_1 (v), \ldots ,\varphi _n (v))$：获利分配向量
• 其中合作获利函数$v$满足两条性质：$v(\varnothing)=0$、$v(S\cup T)\geqslant v(S)+v(T)$，其中 $S$, $T$ 是 $I$ 中元素构成的不相交的两个集合.

---

Shapley 公理

为了确定 $\Phi (v)$，Lloyd Shapley 于 1953 年提出了一组公理：

• 对称性：分配方案与成员的编号无关；
• 有效性：对每次合作均无贡献者，不应从合作收益中分成；
• 合理性：合作收益必须全部分完；
• 可加性： $n$ 人进行两项合作时，每人分配的所得应是两项
  合作分配所得之和.

---

Shapley 证明了满足这组公理的 $\Phi (v)$ 的解是唯一的，其解为：

$$\varphi _i (v) = \sum_{s \in S_i } {w(|s|)[v(s) - v(s -\{i\})]}, \quad i = 1,2, \ldots ,n$$

• $S_i$ 是 $I$ 中包含成员 $i$ 的所有子集，$|s|$ 是集合 $s$ 的元素个数
• $[v(s) - v(s - \{i\})]$ 即成员 $i$ 对合作 $s$ 的贡献
• 加权因子 $w(|s|) = \frac{(|s| - 1)!(n - |s|)!}{n!} = \frac{1}{n} \cdot \frac{1}{C_{n - 1}^{|s| - 1}}$
• $\Phi(v)$ 称为由特征函数 $v$ 定义的合作的 Shapley 值

---

求解：甲的获利

$$\boxed{\begin{array}{c|cccc} S_1 & 1 & 1,2 & 1,3 & 1,2,3\\ \hline v(s) & 1 & 7 & 5 & 10\\ v(s-\{1\}) & 0 & 1 & 1 & 4\\ v(s)-v(s-\{1\}) & 1 & 6 & 4 & 6\\ |s| & 1 & 2 & 2 & 3\\ w(|s|) & 1/3 & 1/6 & 1/6 & 1/3\\ w(|s|)[v(s)-v(s-\{1\})] & 1/3 & 1 & 2/3 & 2 \end{array}}$$

• 由此可得 $\varphi_1(v)=4$，类似地，可得 $\varphi_2(v)=3.5$，$\varphi_3(v)=2.5$

---

污水处理问题中的费用分担：1 的贡献

$$\boxed{\begin{array}{c|cccc} S_1 & 1 & 1,2 & 1,3 & 1,2,3\\ \hline v(s) & 0 & 452.3 & -38.8 & 879.7\\ v(s-\{1\}) & 0 & 0 & 0 & 244.3\\ v(s)-v(s-\{1\}) & 0 & 452.3 & -38.8 & 635.4\\ |s| & 1 & 2 & 2 & 3\\ w(|s|) & 1/3 & 1/6 & 1/6 & 1/3\\ w(|s|)[v(s)-v(s-\{1\})] & 0 & 75.38 & -6.5 & 211.8 \end{array}}$$

• 由此可得 $\varphi_1(v)=280.72$，类似地，可得 $\varphi_2(v)=422.27$，$\varphi_3(v)=176.68$

---

结果的应用

• 三个城市在合作建厂总的节约开支中，分别的贡献额度为：280.72, 422.27 和 176.68 万元
• 三个城市单独建厂的费用分别为：2296.1，1596 和 2296.1 万元
• 最终，三个城市分摊的成本费用（=单独建厂费用-节约贡献额度）分别为：2115.38，1173.73 和 2119.42 万元.

---

Shapley 定理的应用

例：派别在团体中的权重

• 90 人的团体由 3 个派别组成，人数分别为 40, 30, 20人.
• 团体表决时需过半数的赞成票方可通过.
• 假定每个派别一致行动，即所有成员同时投赞成票或反对票.
• 试计算各派别在团体中的权重.

---

分析

• 团体 $I=\{1,2,3\}$，依次代表 3 个派别.
• 定义特征函数 $v(s)=\left\{ \begin{array}{lc} 1, & |s|>45 \\ 0, & {\rm otherwise}\end{array}\right.$
• 合作获利 $v(\phi)=0,\ v(1)=v(2)=v(3)=0$, $v(1\cup 2)=v(1\cup 3)=v(2\cup 3)=v(I)=1$,
• $\varphi_1=\varphi_2=\varphi_3=1/3$

---

Shapley-Shubik Power Index

• 一个团体在决策中的权重，并不是简单的与其规模成正比.
• Shapley 与 Shubik 于 1954 年基于 Shapley 值模型提出一种刻画在投票过程中投票人权重的方法，称为 Shapley-Shubik 权力指数.
• 投票系统中某投票人的 Shapley-Shubik 权力指数是指，在所有可能的投票序列中，该投票人投出关键一票的次数与投票序列总数的比值.
  
  • 所谓关键一票是指，在某一投票序列中，在该投票人投赞成票之前，不可能通过决议，而在其投赞成票之后，有可能通过决议.

---

分析

• 设一次投票中有 $k$ 个团体，各有票数 $a_1$, $a_2$,$\ldots$, $a_k$.
• 若在这次投票中，形成一个决议至少需要 $n$ 票，则这个投票系统记为 $[n: a_1, a_2,\ldots, a_k]$
• 例如，在有 4 个团体 A、B、C、D 的投票系统中，各团体的票数分别为：3、2、1、1 票，设通过某项决议至少需要 4 票，该系统可记为 $[4: 3, 2, 1, 1]$
• 共有 24 种可能的投票序列，如下表，在每个序列中，投出关键一票的团体标记为绿色

---

$$\boxed{\begin{array}{c|c|c|c|c|c} A\bbox[lightgreen]{B}CD & A\bbox[lightgreen]{B}DC & A\bbox[lightgreen]{C}BD & A\bbox[lightgreen]{C}DB & A\bbox[lightgreen]{D}BC & A\bbox[lightgreen]{D}CB \\ \hline B\bbox[lightgreen]{A}CD & B\bbox[lightgreen]{A}DC & BC\bbox[lightgreen]{A}D & BC\bbox[lightgreen]{D}A & BD\bbox[lightgreen]{A}C & BD\bbox[lightgreen]{C}A \\ \hline C\bbox[lightgreen]{A}BD & C\bbox[lightgreen]{A}DB & CB\bbox[lightgreen]{A}D & CB\bbox[lightgreen]{D}A & CD\bbox[lightgreen]{A}B & CD\bbox[lightgreen]{B}A \\ \hline D\bbox[lightgreen]{A}BC & D\bbox[lightgreen]{A}CB & DB\bbox[lightgreen]{A}C & DB\bbox[lightgreen]{C}A & DC\bbox[lightgreen]{A}B & DC\bbox[lightgreen]{B}A \end{array}}$$

• 其中 A 投出关键一票 12 次，B、C、D 均投出关键一票各 4 次.
• 则 A 的 Shapley-Shubik 权力指数为 $1/2$，B、C、D均为 $1/6$.
• 注意到，B 虽然比 C、D 多一张票，但是实际的权重与 C 和 D 是一样的. 或者说，如果 A 想要控制投票结果而与其他团体结盟的话，B、C、D的地位是对等的.

---

Banzhaf Power Index

• Banzhaf 权力指数是另外一种衡量投票者在投票中对结果影响力的模型.
• 在一个选票组合中，如果某个投票人改变其决定，投票结果就会改变，那么该投票人就是这个投票组合的关键选民.
• 计算 Banzhaf 权力指数时，先列出所有投票结果为正的组合，目标投票人是关键选民的次数与所有关键选民总数的比值，就是该投票人的 Banzhaf 权力指数.

---

示例

在投票系统 $[9: 7, 5, 4, 1]$中，所有结果为通过的投票组合以及对应的关键选民如下：

• $\boxed{\begin{array}{l|l|l}\{7, 5, 4, 1\}: \text{无} & \{7, 5, 4\}: \text{无} & \{7, 5, 1\}:\;7,5\\ \{7, 4, 1\}:\;7,4 & \{5, 4, 1\}:\;5,4 & \{7, 5\}:\;7,5\\ \{7, 4\}:\;7,4 & \{5, 4\}:\;5,4\end{array}}$
• 因此，各人的权力指数分别为 $1/3$, $1/3$, $1/3$, $0$.
  
  • 恰好各人的 Shapley-Shubik 指数也是一样的.

---

课后思考题

考虑一个包含 A、B、C 和 D 四位投票人的加权投票系统，$[50:31,21,11,v]$. 整数 $v$ 取何值，可使得投票人 D 的 Shapley-Shubik 指数等于 $1/12$？