第二十七讲 一元线性回归

概率论与数理统计 讲义 NUDT 2023SP

---

---

27.1 回归的概念

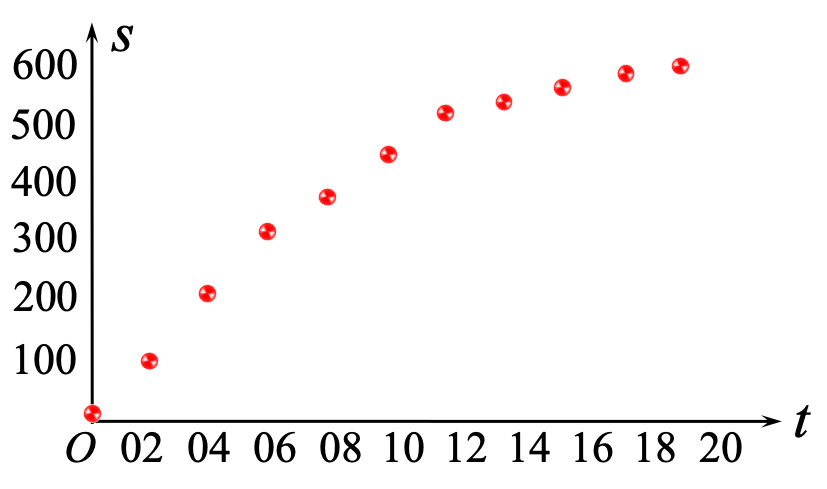
例 某型战机降落时，机载仪器记录的前 20 秒滑行时间 $t$（秒）与滑行距离 $s$（米）的数据如下

$$\boxed{\begin{array}{c|ccccccccccc} t & 0 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20\\\hline s & 0 & 112.5 & 217.3 & 306.5 & 383.6 & 449.6 & 504.9 & 544.4 & 574.9 & 594.5 & 602.1 \end{array}}$$

• 由牛顿运动学定律可推出飞机降落时的滑行时间 $t$（秒）与滑行距离 $s$（米）应该满足关系：$s=-at^2+bt\;(a,b>0)$
• 以上数据真的满足关系 $s=-at^2+bt$ 吗？

---

变量的非确定性关系

• 理想状态下，$s$ 和 $t$ 之间存在 确定性关系 $s=-at^2+bt$
• 但在现实情况下，观测数据总是存在一定的偏差
  
  • 导致偏差的原因包括（但不限于）：测量误差、风的干扰、人为因素
• 非确定的模型：$\bbox[yellow]{s=-at^2+bt+\varepsilon}$
  
  • 随机变量 $\varepsilon$ 表示各种随机因素导致的偏差
  • 通常假设：$E(\varepsilon)=0$，$D(\varepsilon)>0$

---

相关关系与回归分析

• 相关关系（correlativity）：变量之间存在的相互依存但由于随机因素干扰而导致的非确定性关系
• 一般形式：$\begin{cases} y=f(\boldsymbol{x})+\varepsilon\\ E(\varepsilon)=0,\;D(\varepsilon)>0 \end{cases}$，$\boldsymbol{x}=(x_1,x_2,...,x_k)$
• 利用观测的得到的数据，对系统输出 $y$ 与输入 $\boldsymbol{x}$ 之间的依存关系 $f$ 以及随机误差 $\varepsilon$ 进行统计推断，称为 回归分析 （Regression Analysis）.
• 一元线性回归 特指回归分析中 $f$ 为一元线性函数的情形

---

回归

• 一般认为，数学上的回归一词是英国人类学家和气象学家 Galton 引入的.
• Galton 发现：特别高的父母普遍有比他们矮的孩子，而特别矮的父母的孩子通常比父母要高.
• 他把这种现象称为 “遗传身高向平庸的回归”，这个概念现在变成了数学上更广义的 “向均值回归” （regression toward the mean）.
• Galton 利用图表与数据点发现了父母身高与孩子身高之间的关联，并最早把这种关系的强度用 “相关系数” 来刻画.

---

统计分析的诞生

• Karl Pearson 在 Galton 的基础上完善了相关性这一概念，并于 1911 年在伦敦大学学院（UCL）创立了世界上第一个大学统计系
• "统计分析开辟了一个全新的领域，它让我们在无法完全了解确切原因的情况下仍然可以利用有效的信息"
• Galton was an innovator in the field of statistics, the first to recognize the “wisdom of the crowd.”

---

27.2 一元线性回归

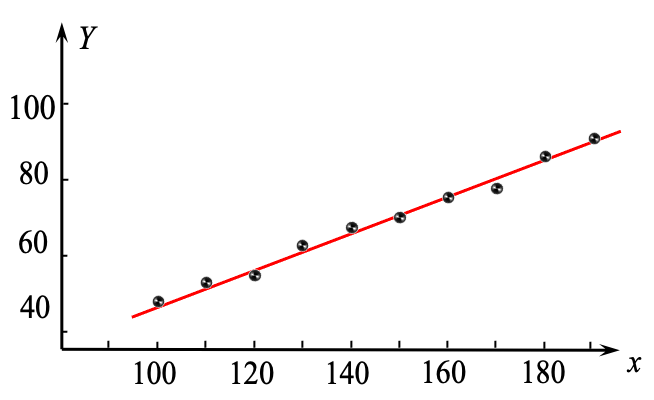
例 为研究某化学反应过程中，温度 $x$ (℃) 对产品得率 $y$（%） 的影响，测得数据如下：

$$\boxed{\begin{array}{c|cccccccccc} x & 100 & 110 & 120 & 130 & 140 & 150 & 160 & 170 & 180 & 190\\ \hline y & 45 & 51 & 54 & 61 & 66 & 70 & 74 & 78 & 85 & 89 \end{array}}$$

试研究 $y$ 与 $x$ 之间的关系.

---

观察与推测

• 尽管存在一定的偏差，但不难看出所得到的数据大致分布在一条直线上
• 由此，推测 $x$ 与 $y$ 之间存在较强的线性依存关系
• 建立回归模型
  
  • $\bbox[yellow]{\begin{cases} y=\beta_0+\beta_1x+\varepsilon\\ E(\varepsilon)=0,\;D(\varepsilon)>0 \end{cases}}$
• 问题一：如何求得 $\beta_0$，$\beta_1$？
• 问题二： $\varepsilon$ 具有哪些统计特性？

---

一元线性回归模型

$$\begin{cases} y=\beta_0+\beta_1x+\varepsilon\\ E(\varepsilon)=0,\;D(\varepsilon)>0 \end{cases}$$

• 因变量 $y$：可观测的指标；自变量 $x$：与 $y$ 相关的因素（因子）
• 回归系数 $\beta_0,\;\beta_1$：能够反映 $y$ 与 $x$ 的关系的最适当的参数
• 随机误差 $\varepsilon$：无法测量的随机扰动
  
  • $E(\varepsilon)=0$：$\varepsilon$ 中不包含系统误差
  • $D(\varepsilon)>0$：方差存在，意味着误差的波动幅度有限

---

一元线性回归模型研究的问题

$$\begin{cases} y=\beta_0+\beta_1x+\varepsilon\\ E(\varepsilon)=0,\;D(\varepsilon)>0 \end{cases}$$

1. 回归系数 $\beta_0,\beta_1$ 及方差 $D(\varepsilon)=\sigma^2$ 的点估计
2. 线性模型的假设是否符合实际？
3. 怎样将线性模型用于预测和控制？
4. 可否/如何将非线性回归问题转化为线性回归问题来处理？

---

27.3 回归中的点估计

取 $x$ 的不全相同的值 $x_1,x_2,...,x_n$ 进行 $n$ 次独立试验，得到 $y$ 的观测值为 $y_1,y_2,...,y_n$（称为试验的样本）

$$\begin{cases} y_i=\beta_0+\beta_1x_i+\varepsilon_i\\ E(\varepsilon_i)=0,\;D(\varepsilon_i)>0\\ \varepsilon_1,\varepsilon_2,...,\varepsilon_n\text{ 独立同分布} \end{cases},\; i=1,2,...,n.$$

---

回归系数的最小二乘估计

若 $\hat{\beta}_0$，$\hat{\beta}_1$ 满足

$$Q(\hat{\beta}_0,\hat{\beta}_1)=\min_{\beta_0,\beta_1}Q(\beta_0,\beta_1),$$

则称 $\hat{\beta}_0$,$\hat{\beta}_1$ 分别是 $\beta_0$,$\beta_1$ 的 最小二乘估计（Least Square Estimate, LSE）.

• $\bbox[yellow]{Q(\beta_0,\beta_1)=\sum\limits_{i=1}^n\left[y_i-(\beta_0+\beta_1x_i)\right]^2}$ 称为估计的 均方误差.

---

LSE 的几何意义

---

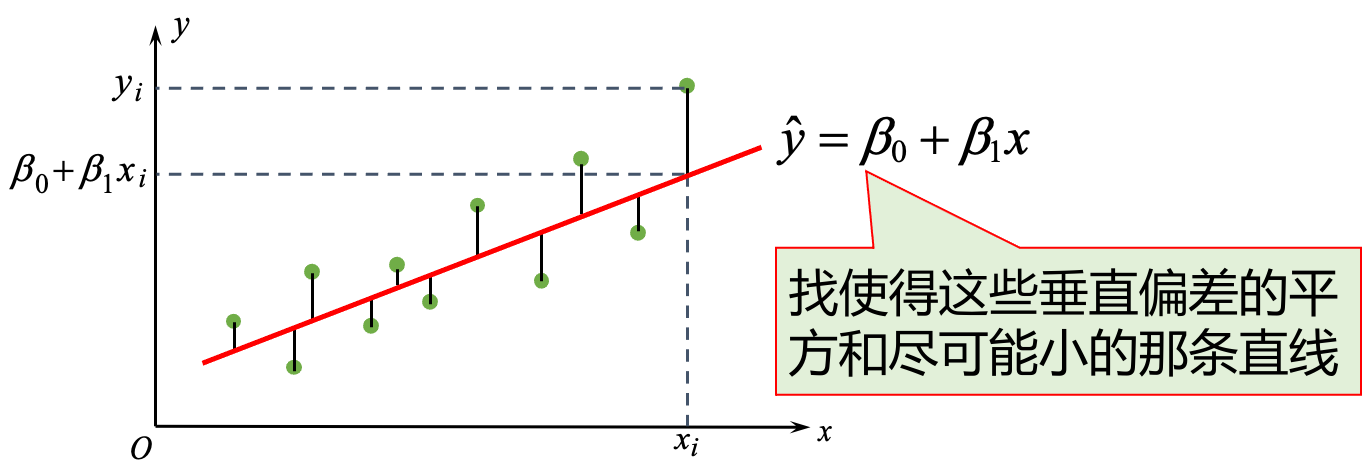
LSE 的求解

• 令 $\triangledown Q=0$，即 $\begin{cases}\dfrac{\partial Q}{\partial \beta_0}=-2\sum\limits_{i=1}^{n}\left[y_i-(\beta_0+\beta_1x_i)\right]=0\\\dfrac{\partial Q}{\partial \beta_1}=-2\sum\limits_{i=1}^{n}x_i\left[y_i-(\beta_0+\beta_1x_i)\right]=0\end{cases}$
• 整理得到 正规方程组 $\begin{cases} n\beta_0+\left(\sum\limits_{i=1}^{n}x_i\right)\beta_1=\sum\limits_{i=1}^{n}y_i\\ \left(\sum\limits_{i=1}^{n}x_i\right)\beta_0+\left(\sum\limits_{i=1}^{n}x_i^2\right)\beta_1=\sum\limits_{i=1}^{n}x_iy_i \end{cases}$

---

正规方程组的解

• $x_1,...,x_n$ 不全相同，故 $\begin{vmatrix} n & \sum\limits_{i=1}^{n}x_i \\ \sum\limits_{i=1}^{n}x_i & \sum\limits_{i=1}^{n}x_i^2 \end{vmatrix}=n \sum\limits_{i=1}^{n}x_i^2-\left( \sum\limits_{i=1}^{n}x_i \right)^2=n \sum\limits_{i=1}^{n}(x-\overline{x})^2\ne 0$
• 由此可知正规方程组有唯一解 $\begin{cases} \hat{\beta}_1=\dfrac{\sum\limits_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sum\limits_{i=1}^{n}(x_i-\overline{x})^2}\\ \hat{\beta}_0=\overline{y}-\hat{\beta}_1\overline{x} \end{cases}$
• 称 $\hat{y}=\hat{\beta}_0+\hat{\beta}_1x$ 为 $y$ 关于 $x$ 的 经验回归方程（经验方程）. 对应的直线称为 回归直线 或 拟合直线.

---

简写符号

• 记 $L_{xx}= \sum\limits_{i=1}^n(x_i-\overline{x})^2= \sum\limits_{i=1}^{n}x_i^2-\dfrac{1}{n}\left(\sum\limits_{i=1}^{n}x_i\right)^2$
• 记 $L_{yy}= \sum\limits_{i=1}^n(y_i-\overline{y})^2=\sum\limits_{i=1}^{n}y_i^2-\dfrac{1}{n}\left(\sum\limits_{i=1}^{n}y_i\right)^2$
• 记 $L_{xy}= \sum\limits_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})=\sum\limits_{i=1}^{n}x_iy_i-\dfrac{1}{n}\left(\sum\limits_{i=1}^{n}x_i\right)\left(\sum\limits_{i=1}^{n}y_i\right)$
• 则 $\bbox[yellow]{\hat{\beta}_0=\dfrac{L_{xy}}{L_{xx}},\;\hat{\beta}_0=\overline{y}-\hat{\beta}_1\overline{x}}$

---

例：化学实验得率与温度的关系

$$\boxed{\begin{array}{c|cccccccccc} x & 100 & 110 & 120 & 130 & 140 & 150 & 160 & 170 & 180 & 190\\ \hline y & 45 & 51 & 54 & 61 & 66 & 70 & 74 & 78 & 85 & 89 \end{array}}$$

• 计算各项数据：$\boxed{\begin{array}{ccccccccccc} \sum x & \sum y & \sum x^2 & \sum y^2 & \sum xy\\ \hline 1450 & 673 & 218500 & 47225 & 101570 \end{array}}$
• 进而得到 $L_{xx}=8250$，$L_{xy}=3985$
• 于是 $\hat{\beta}_1=\dfrac{L_{xy}}{L_{xx}}=0.483$，$\hat{\beta}_0=-2.7394$
• 回归方程：$\hat{y}=-2.7394+0.483 x$.

---

LSE 的性质

性质1 $\hat{\beta}_0$、$\hat{\beta}_1$ 是样本的线性函数.

$$\bbox[yellow]{\hat{\beta}_1=\dfrac{L_{xy}}{L_{xx}}=\sum\limits_{i=1}^n\dfrac{x_i-\overline{x}}{L_{xx}}y_i,\quad \hat{\beta}_0=\overline{y}-\hat{\beta}_1\overline{x}=\sum\limits_{i=1}^n\left(\dfrac{1}{n}-\overline{x}\dfrac{x_i-\overline{x}}{L_{xx}}\right)y_i.}$$

性质2 $\hat{\beta}_0$、$\hat{\beta}_1$ 分别是 $\beta_0$、$\beta_1$ 的无偏估计，即：

$$\bbox[yellow]{E(\hat{\beta}_1)=\beta_1,\quad E(\hat{\beta}_0)=\beta_0}$$

---

证明： $\hat{\beta}_0$、$\hat{\beta}_1$ 是样本的线性函数.

• 因为 $\sum\limits_{i=1}^n(x_i-\overline{x})=0$，
• 故 $L_{xy}=\sum\limits_{i=1}^n({x_i-\overline{x}})(y_i-\overline{y})=\sum\limits_{i=1}^n({x_i-\overline{x}})y_i-\overline{y}\sum\limits_{i=1}^n({x_i-\overline{x}})=\sum\limits_{i=1}^n({x_i-\overline{x}})y_i$
• 于是 $\hat{\beta}_1=\dfrac{L_{xy}}{L_{xx}}=\sum\limits_{i=1}^n\dfrac{x_i-\overline{x}}{L_{xx}}y_i$
• $\hat{\beta}_0=\overline{y}-\hat{\beta}_1\overline{x}=\sum\limits_{i=1}^n\left(\dfrac{1}{n}-\overline{x}\dfrac{x_i-\overline{x}}{L_{xx}}\right)y_i$

---

证明： $E(\hat{\beta}_1)=\beta_1,\quad E(\hat{\beta}_0)=\beta_0$

• $E(\hat{\beta}_1)=\sum\limits_{i=1}^n\dfrac{x_i-\overline{x}}{L_{xx}}E(y_i)=\sum\limits_{i=1}^n\dfrac{x_i-\overline{x}}{L_{xx}}(\beta_0+\beta_1x_i)$
  
  • $=\sum\limits_{i=1}^n\beta_1\dfrac{x_i-\overline{x}}{L_{xx}}x_i=\dfrac{\beta_1}{L_{xx}}\sum\limits_{i=1}^n(x_i-\overline{x})(x_i-\overline{x})=\beta_1$
• $E(\hat{\beta}_0)=E(\overline{y})-E(\hat{\beta}_1)\overline{x}=\dfrac{1}{n}\sum\limits_{i=1}^n(\beta_0+\beta_1x_i)-\beta_1\overline{x}$
  
  • $=\dfrac{1}{n}\sum\limits_{i=1}^n\beta_0+\beta_1\dfrac{1}{n}\sum\limits_{i=1}^nx_i-\beta_1\overline{x}=\beta_0$

---

性质3 $\bbox[yellow]{\mathrm{Cov}(\overline{y},\hat{\beta}_1)=0}$.

性质4 $\bbox[yellow]{D(\hat{\beta}_1)=\dfrac{\sigma^2}{L_{xx}}}$，$\bbox[yellow]{D(\hat{\beta}_0)=\sigma^2\left(\dfrac{1}{n}+\dfrac{\overline{x}^2}{L_{xx}}\right)}$.

• 对 $\beta_0$、$\beta_1$ 的估计效果与 $\sigma^2,n,\overline{x},L_{xx}$ 相关
• 设计试验的原则
  
  • 试验次数 $n$ 不能太小
  • $x_1,x_2,...,x_n$ 可以取正负值时，尽量使得 $\overline{x}=0$
  • $x_1,x_2,...,x_n$ 约分散越好，即 $L_{xx}$ 越大越好

---

证明： $\mathrm{Cov}(\overline{y},\hat{\beta}_1)=0$.

• $\mathrm{Cov}(\overline{y},\hat{\beta}_1)=\mathrm{Cov}\left(\beta_0+\beta_1\overline{x}+\dfrac{1}{n}\sum\limits_{i=1}^n\varepsilon_i,\sum\limits_{j=1}^n\dfrac{x_j-\overline{x}}{L_{xx}}y_j\right)$
  
  • $=\dfrac{1}{nL_{xx}}\mathrm{Cov}\left(\sum\limits_{i=1}^n\varepsilon_i,\sum\limits_{j=1}^n(x_j-\overline{x})y_j\right)$
  • $=\dfrac{1}{nL_{xx}}\mathrm{Cov}\left(\sum\limits_{i=1}^n\varepsilon_i,\sum\limits_{j=1}^n(x_j-\overline{x})(\beta_0+\beta_1x_j+\varepsilon_j)\right)$
  • $=\dfrac{1}{nL_{xx}}\mathrm{Cov}\left(\sum\limits_{i=1}^n\varepsilon_i,\sum\limits_{j=1}^n(x_j-\overline{x})\varepsilon_j\right)=\dfrac{1}{nL_{xx}}\sum\limits_{i=1}^n\sum\limits_{j=1}^n(x_j-\overline{x})\mathrm{Cov}\left(\varepsilon_i,\varepsilon_j\right)$
  • $=\dfrac{1}{nL_{xx}}\sum\limits_{i=1}^n(x_j-\overline{x})\sigma^2=\dfrac{\sigma^2}{nL_{xx}}\sum\limits_{i=1}^n(x_j-\overline{x})=0$

---

证明： $D(\hat{\beta}_1)=\dfrac{\sigma^2}{L_{xx}}$

• $D(\hat{\beta}_1)=D\left(\dfrac{L_{xy}}{L_{xx}}\right)=\dfrac{1}{L_{xx}^2}D\left(\sum\limits_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})\right)$
  
  • $=\dfrac{1}{L_{xx}^2}D\left(\sum\limits_{i=1}^n(x_i-\overline{x})y_i\right)=\dfrac{1}{L_{xx}^2}\sum\limits_{i=1}^n(x_i-\overline{x})^2D\left(y_i\right)$
  • $=\dfrac{1}{L_{xx}^2}\sum\limits_{i=1}^n(x_i-\overline{x})^2D\left(\varepsilon_i\right)=\dfrac{1}{L_{xx}^2}\sum\limits_{i=1}^n(x_i-\overline{x})^2\sigma^2=\dfrac{\sigma^2}{L_{xx}}$

---

证明： $D(\hat{\beta}_0)=\sigma^2\left(\dfrac{1}{n}+\dfrac{\overline{x}^2}{L_{xx}}\right)$

• $D(\hat{\beta}_0)=D\left(\overline{y}-\hat{\beta}_1\overline{x}\right)=D\left(\overline{y}\right)+\overline{x}^2D\left(\hat{\beta}_1\right)-2\overline{x}\mathrm{Cov}(\overline{y},\hat{\beta}_1)$
  
  • $=D\left(\dfrac{1}{n}\sum\limits_{i=1}^ny_i\right)+\dfrac{\overline{x}^2}{L_{xx}}\sigma^2=\dfrac{1}{n^2}\sum\limits_{i=1}^nD\left(y_i\right)+\dfrac{\overline{x}^2}{L_{xx}}\sigma^2$
  • $=\dfrac{1}{n}\sigma^2+\dfrac{\overline{x}^2}{L_{xx}}\sigma^2=\sigma^2\left(\dfrac{1}{n}+\dfrac{\overline{x}^2}{L_{xx}}\right)$

---

27.4 方差的无偏估计

残差平方和（Residual Sum of Squares）

$$\bbox[lightgreen]{Q_e=\sum\limits_{i=1}^n(y_i-\hat{y}_i)^2.}$$

• $Q_e$ 反映了拟合值与观察值整体的偏差大小
• 性质1 $Q_e=L_{yy}-\hat{\beta}_1^2L_{xx}$
• 性质2 $\bbox[yellow]{E(Q_e)=(n-2)\sigma^2}$
• 推论 $\hat{\sigma}_e^2=\dfrac{Q_e}{n-2}$ 是 $\sigma^2$ 的无偏估计，称 $\hat{\sigma}_e^2$ 为 剩余方差.

---

证明： $Q_e=L_{yy}-\hat{\beta}_1^2L_{xx}$

• $Q_e=\sum\limits_{i=1}^n(y_i-\hat{y}_i)^2=\sum\limits_{i=1}^n[(y_i-\overline{y})-\hat{\beta}_1(x_i-\overline{x})]^2$
  
  • $=\sum\limits_{i=1}^n(x-\overline{x})^2-2\hat{\beta}_1\sum\limits_{i=1}^n(y_i-\overline{y})(x_i-\overline{x})+\hat{\beta}_1^2\sum\limits_{i=1}^n(x_i-\overline{x})^2$
  • $=L_{yy}-2\hat{\beta}_1L_{xy}+\hat{\beta}_1^2L_{xx}=L_{yy}-2\hat{\beta}_1\hat{\beta}_1L_{xx}+\hat{\beta}_1^2L_{xx}$
  • $=L_{yy}-\hat{\beta}_1^2L_{xx}$

---

证明： $E(Q_e)=(n-2)\sigma^2$

• $E(Q_e)=E(L_{yy}-\hat{\beta}_1^2L_{xx})=E(L_{yy})-E(\hat{\beta}_1^2)L_{xx}$
  
  • $=\sum\limits_{i=1}^nE[(y_i-\overline{y})^2]-[D(\hat{\beta}_1)+(E(\hat{\beta}_1))^2]L_{xx}$
  • $=\sum\limits_{i=1}^n[E(y_i^2)-nE(\overline{y}^2)]- [D(\hat{\beta}_1)+(E(\hat{\beta}_1))^2]L_{xx}$
  • $=\sum\limits_{i=1}^n\left[\sigma^2+(\beta_0+\beta_1x_i)^2-\left(\dfrac{\sigma^2}{n}+(\beta_0+\beta_1\overline{x})^2\right)\right]-(\sigma^2+\beta_1^2L_{xx})$
  • $=(n-2)\sigma^2+\beta_1^2\sum\limits_{i=1}^n(x_i^2-n\overline{x}^2)-\beta_1^2L_{xx}=(n-2)\sigma^2$

---

例：化学实验得率与温度的关系

$$\boxed{\begin{array}{c|cccccccccc} x & 100 & 110 & 120 & 130 & 140 & 150 & 160 & 170 & 180 & 190\\ \hline y & 45 & 51 & 54 & 61 & 66 & 70 & 74 & 78 & 85 & 89 \end{array}}$$

• $L_{xx}=8250$，$L_{xy}=3985$，$L_{yy}=1932.1$
• $\hat{\beta}_1=\dfrac{L_{xy}}{L_{xx}}=0.483$，$\hat{\beta}_0=-2.7394$
• $Q_e=L_{yy}-\hat{\beta}_1^2L_{xx}=7.46575$
• $\sigma^2$ 的估计：$\hat{\sigma^2}=\dfrac{7.46575}{10-2}=0.933$

---

27.4 正态线性模型

$$\begin{cases} y_i=\beta_0+\beta_1 x_i+\varepsilon_i,\;i=1,2,...,n\\ \bbox[lightgreen]{\varepsilon_1,\varepsilon_2,...,\varepsilon_n\stackrel{iid}{\sim}N(0,\sigma^2)} \end{cases}$$

• 显然，$y_i\sim N(\beta_0+\beta_1x_i,\sigma^2)$
• 似然函数 $L(\beta_0,\beta_1)=\dfrac{1}{2\pi\sigma^2}\exp\left\{-\dfrac{1}{2\sigma^2}\sum\limits_{i=1}^n[y_i-(\beta_0+\beta_1x_i)]^2\right\}$
• $\max\limits_{\beta_0,\beta_1}L(\beta_0,\beta_1)\;\Leftrightarrow\;\min\limits_{\beta_0,\beta_1}\sum\limits_{i=1}^n[y_i-(\beta_0+\beta_1x_i)]^2$
• 在正态线性模型下，$\beta_0$、$\beta_1$ 的 LSE 就是 MLE

---

正态线性模型的性质

1. $\beta_0$、$\beta_1$ 的 LSE 就是 MLE
2. $\sigma^2$ 的 MLE 和无偏估计分别是 $\hat{\sigma}^2=\dfrac{Q_e}{n}$ 和 $\hat{\sigma}_e^2=\dfrac{Q_e}{n-2}$
3. $\bbox[yellow]{\hat{\beta}_0\sim N\left(\beta_0,\sigma^2\left(\dfrac{1}{n}+\dfrac{\overline{x}^2}{L_{xx}}\right)\right)}$，$\bbox[yellow]{\hat{\beta}_1\sim N\left(\beta_1,\dfrac{\sigma^2}{L_{xx}}\right)}$
4. $\bbox[yellow]{\dfrac{Q_e}{\sigma^2}\sim\chi^2(n-2)}$
5. $\overline{y}$, $\hat{\beta}_1$, $Q_e$ 相互独立
6. $\bbox[yellow]{\dfrac{\hat{\beta}_1-\beta_1}{\hat{\sigma}_e^2/\sqrt{L_{xx}}}\sim t(n-2)}$

---

小结

• 一元线性回归模型
• 回归参数的点估计及其性质
• 随机误差的方差的点估计
• 一元正态线性回归模型