第二十六讲 功效函数与最大功效检验

概率论与数理统计 讲义 NUDT 2023SP

---

---

26.1 检验的功效

对于某个假设检验问题

$$H_0:\theta\in\Theta_0,\quad H_1:\theta\in\Theta_1.$$

若在置信水平 $\alpha$ 下求得了一个拒绝域 $W_1$，则称由 $W_1$ 给出了以上假设检验问题在置信水平 $\alpha$ 下的一个检验（test）.

• 给定检验问题和置信水平，拒绝域不唯一性，因此检验也不具有唯一性.

---

哪一个检验 (拒绝域) 更好？

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,1)$ 的样本，$\mu$ 未知，在显著水平 $\alpha$ 下，考虑检验假设问题

$$H_0:\;\mu=0;\quad H_1:\; \mu\ne0.$$

• 检验 $\phi_1$：$W_1=\left\{(x_1,x_2,...,x_n)\bigg||\overline{x}|>\frac{u_{1-\alpha / 2}}{\sqrt{n}}\right\}$
• 检验 $\phi_2$：$W_1'=\left\{(x_1,x_2,...,x_n)\bigg|\overline{x}<\frac{u_{\alpha / 3}}{\sqrt{n}}\text{ 或 }\overline{x}>\frac{u_{1-2 \alpha / 3}}{\sqrt{n}}\right\}$
• 检验 $\phi_3$：$W_1''=\left\{(x_1,x_2,...,x_n)\bigg||\overline{x}|>\frac{u_{1-\alpha / 3}}{\sqrt{n}}\right\}$

---

功效函数

对假设检验问题

$$H_0:\;\theta\in\Theta_0,\quad H_1:\;\theta\in\Theta_1.$$

• 若一个检验 $\phi$ 的拒绝域为 $W_1$, 则对任一 $\theta\in\Theta_1$，检验 $\phi$ 对于备择假设 $H_1$ 在 $\theta$ 处的 功效 (Power) 定义为概率 $\bbox[yellow]{P_{\theta}\{(X_1,X_2,\ldots,X_n)\in W_1\}}$.
• 对任意 $\theta\in\Theta_0\cup\Theta_1$，$\bbox[yellow]{\beta(\theta)=P_{\theta}\left\{\left(X_{1}, X_{2}, \ldots, X_{n}\right) \in W_1\right\}}$ 称为检验 $\phi$ 的 功效函数（势函数, Power Function）.

---

注：功效函数的意义

$(X_1,X_2,\ldots,X_n)\in W_1\Leftrightarrow$ 拒绝 $H_0$.

1. 若 $\theta\in\Theta_0$，$H_0$ 成立.
   
   • $\beta(\theta)$ 等于犯第 I 类错误的概率，即 I 类风险.
   • 检验准则一：$\bbox[yellow]{\beta(\theta)\leq \alpha.}$
2. 若 $\theta\in\Theta_1$，$H_1$ 成立.
   
   • $\beta(\theta)$ 等于根据样本观测值作出拒绝原假设的判断是正确的概率.
   • $\bbox[yellow]{1-\beta(\theta)=P_{\theta}\left\{\left(X_{1}, X_{2}, \ldots, X_{n}\right) \notin W_1\right\}}$ 即为 II 类风险.
   • 检验准则二：满足 $\beta(\theta)\leq \alpha$ 的同时，使得 $1-\beta(\theta)$ 尽可能小.

---

例：求功效函数

设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,1)$ 的简单随机样本，其中 $\mu\in(-\infty,+\infty)$ 未知. 在显著水平 $\alpha$ 下，检验假设

$$H_0:\mu=\mu_0,\quad H_1:\mu\ne\mu_0,$$

得到的拒绝域为

$$W_{1}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right)|\sqrt{n}| \overline{x}-\mu_{0} |>u_{1-\alpha / 2}\right\}$$

试求该检验的功效函数 $\beta(\mu)$.

---

解：

• $\beta(\mu)=P_{\mu}\left\{\left(X_{1}, X_{2}, \cdots, X_{n}\right) \in W_{1}\right\}$
  
  • $=P_{\mu}\left\{\sqrt{n}\left|\overline{X}-\mu_{0}\right|>u_{1-\alpha / 2}\right\}$
  • $=P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu_{0}\right)<-u_{1-\alpha / 2}\right\}+P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu_{0}\right)>u_{1-\alpha / 2}\right\}$
  • $=P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu\right)<-u_{1-\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right\}+P_{\mu}\left\{\sqrt{n}\left(\overline{X}-\mu\right)>u_{1-\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right\}$
  • $=\Phi\left(-u_{1-\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right)+\Phi\left(-u_{1-\alpha / 2}-\sqrt{n}(\mu_0-\mu)\right)$
  • $=\Phi\left(u_{\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right)+\Phi\left(u_{\alpha / 2}-\sqrt{n}(\mu_0-\mu)\right)$

---

分析： 本例中

$$\beta(\mu)=\Phi\left(u_{\alpha / 2}+\sqrt{n}\left(\mu-\mu_{0}\right)\right)+\Phi\left(u_{\alpha / 2}-\sqrt{n}\left(\mu-\mu_{0}\right)\right)$$

• $\beta(\mu)$ 的图形关于 $\mu=\mu_0$ 对称.
• $\beta\left(\mu_{0}\right)=\alpha$.
• $\mu\ne\mu_0$ 时，$\beta(\mu)>\alpha$.

---

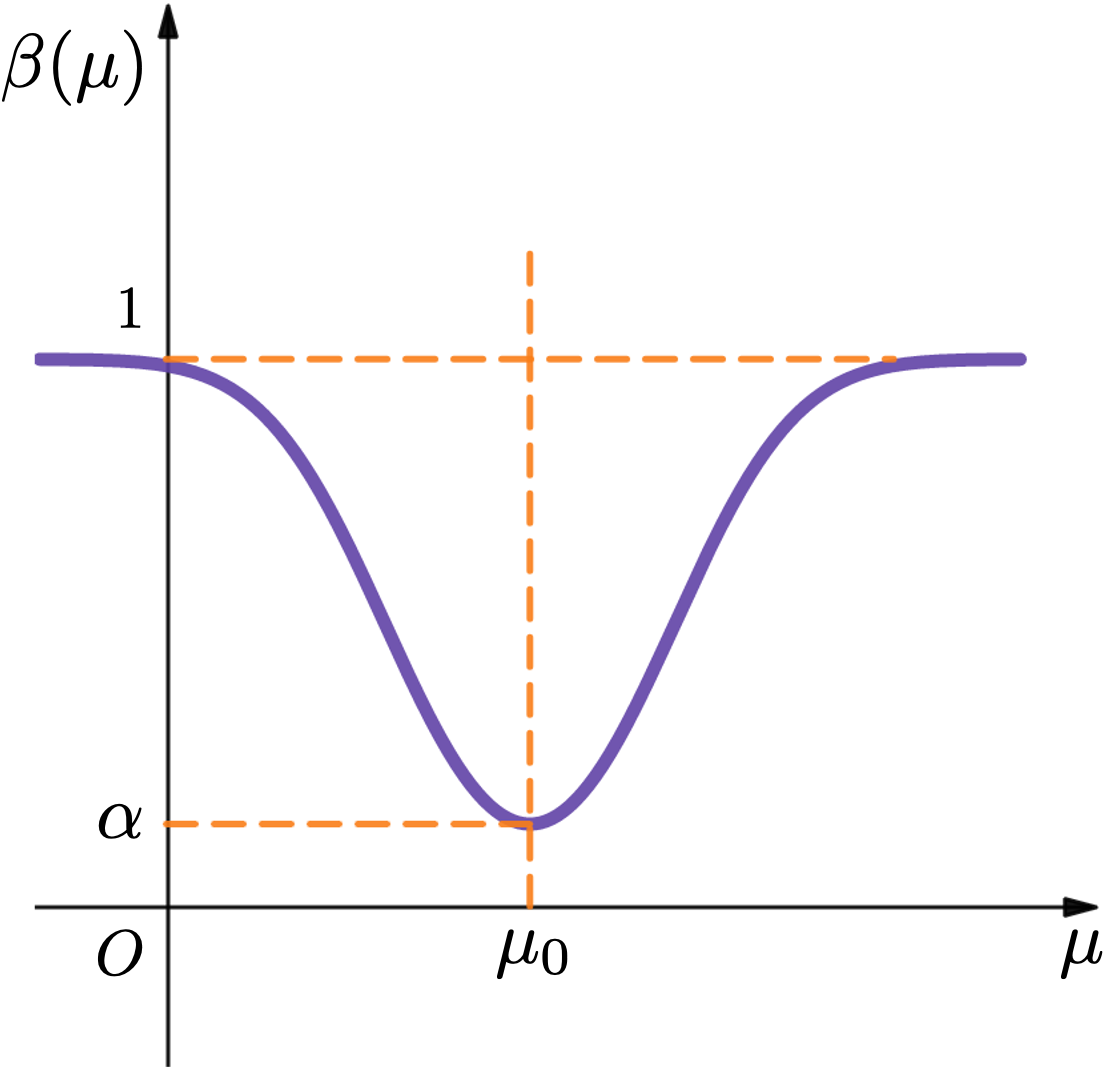
II 类风险与样本容量

• 本例中, 固定样本容量 $n$.
  
  • $\mu$ 离 $\mu_0$ 越远，$\beta(\mu)$ 越接近 $1$，检验效果越好.
  • 若 $\mu$ 和 $\mu_0$ 很接近，则 $1-\beta(\mu)\approx1-\alpha$.
    
    • 无法同时使两类风险都很小！
• 在 I 类风险可控的前提下，可以通过增加样本容量来使得 II 类风险尽可能小.

---

II 类风险

本例中，

• $1-\beta(\mu)$
  
  • $=1-\Phi\left(u_{\alpha / 2}+\sqrt{n}(\mu_0-\mu)\right)-\Phi\left(u_{\alpha / 2}-\sqrt{n}(\mu_0-\mu)\right)$
  • $=\Phi\left(u_{1-\alpha / 2}-\sqrt{n}(\mu-\mu_0)\right)-\Phi\left(u_{\alpha / 2}-\sqrt{n}(\mu-\mu_0)\right)$
  • $=\Phi\left(u_{1-\alpha / 2}-\sqrt{n}(\mu_0-\mu)\right)-\Phi\left(u_{\alpha / 2}-\sqrt{n}(\mu_0-\mu)\right)$
  • $=\Phi\left(u_{1-\alpha / 2}-\sqrt{n}|\mu-\mu_0|\right)-\Phi\left(u_{\alpha / 2}-\sqrt{n}|\mu-\mu_0|\right)$

---

II 类风险的控制

本例中，如果已知 $|\mu-\mu_0|\geqslant\delta>0$ ，对于给定的 $\varepsilon>0$，要使 II 类风险

$$1-\beta(\mu)=\Phi\left(u_{1-\alpha / 2}-\sqrt{n}|\mu-\mu_0|\right)-\Phi\left(u_{\alpha / 2}-\sqrt{n}|\mu-\mu_0|\right)\leqslant\varepsilon.$$

• 因为 $\lim\limits_{n\to\infty}\Phi\left(u_{\alpha / 2}-\sqrt{n}|\mu-\mu_0|\right)\leq\lim\limits_{n\to\infty}\Phi\left(u_{\alpha / 2}-\sqrt{n}\delta\right)=0.$
• 故当 $n$ 较大时，只须满足 $\Phi\left(u_{1-\alpha / 2}-\sqrt{n}|\mu-\mu_0|\right)\leq\varepsilon$ 即可.
• 又 $\Phi\left(u_{1-\alpha / 2}-\sqrt{n}|\mu-\mu_0|\right)\leq \Phi\left(u_{1-\alpha / 2}-\sqrt{n}\delta\right)$.
• 令 $\Phi\left(u_{1-\alpha / 2}-\sqrt{n} \delta\right) \leqslant \varepsilon$，解得 $n \geqslant\left(\frac{u_{1-\alpha / 2}-u_{\varepsilon}}{\delta}\right)^{2}.$

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,\sigma_0^2)$ 的简单随机样本，其中 $\sigma_0^2$ 已知，$\mu$ 未知. 在显著水平 $\alpha$ 下，检验假设

$$H_0:\mu\leq\mu_0,\quad H_1:\mu>\mu_0.$$

取检验的拒绝域

$$W_1=\left\{(x_1,x_2,...,x_n)\bigg|\frac{\overline{x}-\mu_{0}}{\sigma_{0} / \sqrt{n}}>u_{1-\alpha}\right\},$$

试求该检验的功效函数 $\beta(\mu)$.

---

分析：

• $\beta(\mu)=P_{\mu}\left\{\frac{\overline{X}-\mu_{0}}{\sigma_{0} / \sqrt{n}}>u_{1-\alpha}\right\}$
  
  • $=P_{\mu}\left\{\frac{\overline{X}-\mu}{\sigma_{0} / \sqrt{n}}>u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right\}$
  • $=1-P_{\mu}\left\{\frac{\overline{X}-\mu}{\sigma_{0} / \sqrt{n}} \leq u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right\}$
  • $=1-\Phi\left(u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right)$
• $\beta(\mu)$ 关于 $\mu$ 单调增加.

---

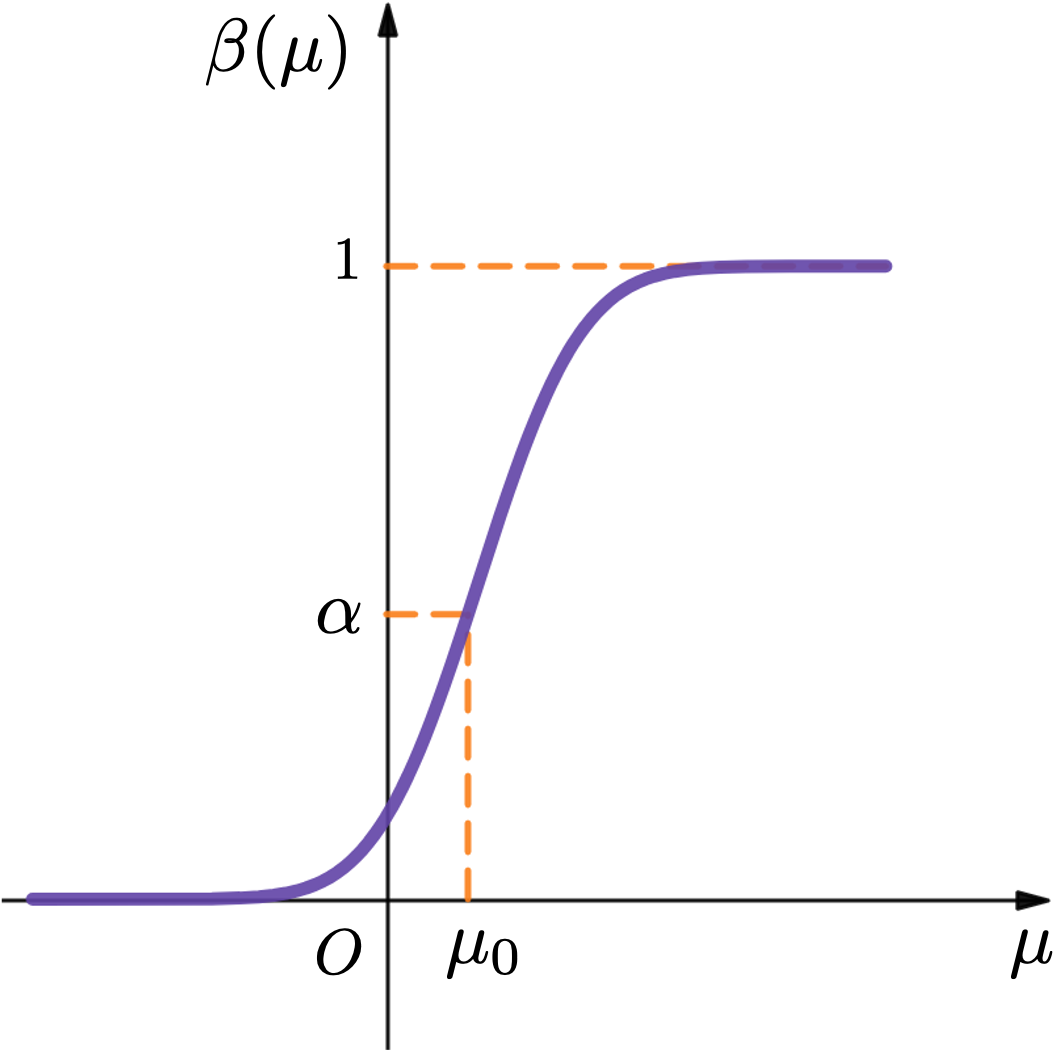
• II 类风险: $1-\beta(\mu)=\Phi\left(u_{1-\alpha}+\frac{\mu_{0}-\mu}{\sigma_{0} / \sqrt{n}}\right)$.
• 设 $\mu_0=0,\sigma_0=1,\alpha=0.05$，要使 $\mu\geq1$ 时，该检验的 II 类风险不大于 $0.10$，则令
  
  • $\Phi\left(u_{0.95}-\sqrt{n}(1-0)\right) \leqslant 0.1$.
  • $\Rightarrow\sqrt{n} \geqslant u_{0.95}+u_{0.90}$.
  • $\Rightarrow n\geqslant 8.57$.
• 结论：样本容量至少为 $9$ 才能使这个检验的 II 类风险不大于 $0.10$.

---

例：工厂产品的质量抽验方案

• 设有一大批产品，产品质量指标 $X\sim N(\mu,\sigma^2)$. 以 $\mu$ 小者为佳.
• 厂方要求所确定的验收方案对高质量的产品 $(\mu\leq\mu_0)$ 能以高于概率 $1-\alpha$ 为买方所接受.
• 买方则要求低质产品 $(\mu\geq\mu_0+\delta,\;\delta>0)$ 能以高于概率 $1-\beta$ 被拒绝.
• $\alpha,\beta$ 由厂方与买方协商给出，并采取一次抽样以确定该批产品是否为买方所接受.
• 问应怎样安排抽样方案.
• 已知 $\mu_0=120,\delta=20$, 且由工厂长期经验知 $\sigma^2=900$. 又经商定 $\alpha,\beta$ 均取为 $0.05$.

---

分析：

• 考虑显著性水平为 $\alpha$ 的检验问题：$H_0:\mu\leq\mu_0,\;H_1:\mu>\mu_0$.
• 且要求当 $\mu\geq\mu_0+\delta$ 时 II 类风险不超过 $1-\beta(\mu)\leq\beta$.
• 拒绝域 $W_1:\frac{\overline{x}-\mu_0}{\sigma/\sqrt{n}}\geq u_{1-\alpha}$.
• $\beta(\mu)=P_{\mu}\left\{ \frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\geq u_{1-\alpha} \right\}$
• $=P_{\mu}\left\{ \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\geq u_{1-\alpha}-\frac{\mu-\mu_0}{\sigma/\sqrt{n}} \right\}=\Phi\left(\frac{\mu-\mu_0}{\sigma/\sqrt{n}}-u_{1-\alpha} \right).$

---

• $\beta(\mu)=\Phi\left(\frac{\mu-\mu_0}{\sigma/\sqrt{n}}-u_{1-\alpha} \right).$
• 现要求当 $\mu\geq\mu_0+\delta$ 时 $1-\beta(\mu)\leq \beta$.
• 也即 $\beta(\mu)\geq 1-\beta$，由此解得 $n\geq\left[ \frac{(u_{1-\alpha}+u_{1-\beta})\sigma}{\delta} \right]^2.$
• 代入数据计算得 $n\geq 24.35$.
• 结论： 取 $n=25$，当 $\frac{\overline{x}-120}{30/\sqrt{5}}\geq u_{0.05}$，也即 $\overline{x}\geq 129.87$ 时，买方就拒绝这批产品；否则，若 $\overline{x}<129.87$，则买方应接受这批产品.

---

26.2 最大功效检验（MPT）

• 对于同一个假设检验问题，在相同的显著性水平 $\alpha$ 下可以给出不同的检验，这些检验的功效函数是不同的
• 1930s, Neyman- Pearson（N-P准则）：在 Ⅰ 类风险满足显著性水平 $\alpha$ 下，使 Ⅱ 类风险尽可能小，即要求这个检验的功效函数 $\beta(\theta)$ 满足：
  
  • $\bbox[yellow]{\left\{\begin{array}{l}\beta(\theta)\leqslant\alpha,& \theta\in\Theta_0\\ \beta(\theta)\text{尽可能大}, & \theta\in\Theta_1\end{array}\right.}$

---

给定一个参数检验问题，其总体参数 $\theta\in\Theta$，要检验假设

$$H_0:\theta\in\Theta_0,\quad H_1:\theta\in\Theta_1.$$

如果存在一个显著性水平 $\alpha$ 的检验 $\phi^*$，使得对于任意一个显著性水平 $\alpha$ 的检验 $\phi$，均有

$$\beta_{\phi^*}(\theta)\geqslant\beta_{\phi}(\theta),\quad (\theta\in\Theta_1)$$

则称 $\phi^*$ 为这个假设检验问题在显著性水平 $\alpha$ 下的 一致最大功效检验（UMPT, Uniformly Most Powerful Test）.

• 当 $H_1$ 为简单假设时，称为 最大功效检验（MPT）.

---

Neyman-Pearson 基本引理

• 设$X_1, X_2,\ldots, X_n$ 是取自总体 $X$ 的样本, $X$ 的概率密度为 $f(x; \theta)$
• 检验假设 $H_0:\theta=\theta_0, H_1:\theta=\theta_1.$
• 给定显著性水平 $\alpha$, 如果存在临界值 $k$, 使 $P_{\theta_{0}}\left\{\frac{\prod_{i=1}^{n} f\left(X_{i} ; \theta_{1}\right)}{\prod_{i=1}^{n} f\left(X_{i} ; \theta_{0}\right)}>k\right\}=\alpha$,
• 那么，以 $W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) \Bigg| \frac{\prod_{i=1}^{n} f\left(x_{i} ; \theta_{1}\right)}{\prod_{i=1}^{n} f\left(x_{i} ; \theta_{0}\right)}>k\right\}$ 为拒绝域的检验 $\phi^*$ 是该假设检验问题在显著性水平 $\alpha$ 下的最大功效检验.

---

注记

• Neyman-Pearson 基本引理中的检验统计量称为 似然比(Likelihood Ratio)，以上的检验称为 似然比检验.
• $l\left(X_{1}, X_{2}, \cdots, X_{n}\right)=\frac{\prod_{i=1}^{n} f\left(X_{i} ; \theta_{1}\right)}{\prod_{i=1}^{n} f\left(X_{i} ; \theta_{0}\right)}=\frac{L(\theta_1)}{L(\theta_0)}$ ，也即似然函数 $L(\theta)$ 在 $\theta_1,\theta_0$ 处的取值之比.
• 似然函数 $L(\theta)$ 刻画了样本落在 $(x_1,x_2,\ldots,x_n)$ 附近的可能性的大小.
  
  • $H_0$ 成立时，$l\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 应该较小.
  • $H_1$ 成立时，$l\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 应该较大.

---

证明概要：

• 设 $W_1$ 为任一其他检验的拒绝域
• 于是 $P(W_1|\theta_0)\leq P(W_1^*|\theta_0)=\alpha$
• $P(W_1^*|\theta)=P(W_1^*\cap W_1|\theta)+P(W_1^*\cap \overline{W_1}|\theta)$
• $P(W_1|\theta)=P(W_1^*\cap W_1|\theta)+P(\overline{W_1^*}\cap W_1|\theta)$
• 由此即知 $P(W_1^*\cap \overline{W_1}|\theta_0)\geq P(\overline{W_1^*}\cap W_1|\theta_0)$
• 两个检验的功效分别为 $P(W_1^*|\theta_1)$ 和 $P(W_1|\theta_1)$

---

• 以下证明 $P(W_1^*|\theta_1)\geq P(W_1|\theta_1)$
  
  • 也即 $P(W_1^*\cap \overline{W_1}|\theta_1)\geq P(\overline{W_1^*}\cap W_1|\theta_1)$
• $P(W_1^*\cap \overline{W_1}|\theta_1)=\int_{W_1^*\cap \overline{W_1}}L(\theta_1;\boldsymbol{x})\mathrm{d}\boldsymbol{x}$
  
  • $\geq k\int_{W_1^*\cap \overline{W_1}}L(\theta_0;\boldsymbol{x})\mathrm{d}\boldsymbol{x}=kP(W_1^*\cap\overline{W_1}|\theta_0)$
  • $\geq kP(\overline{W_1^*}\cap W_1|\theta_0)=k\int_{\overline{W_1^*}\cap W_1}L(\theta_0;\boldsymbol{x})\mathrm{d}\boldsymbol{x}$
  • $>\int_{\overline{W_1^*}\cap W_1}L(\theta_1;\boldsymbol{x})\mathrm{d}\boldsymbol{x}=P(\overline{W_1^*}\cap W_1|\theta_1)$

---

例：求最大功效检验

设 $X_1, X_2, \ldots, X_n$ 是取自总体 $X\sim N (\mu;1)$ 的简单随机样本，其中 $\mu$ 未知，要检验

$$H_0:\mu=\mu_0,\quad H_1:\mu=\mu_1.$$

其中 $\mu_0<\mu_1$，在显著性水平 $\alpha$ 下，求最大功效检验的拒绝域.

---

分析：

• 似然函数 $L(\mu)=\prod_{i=1}^{n} f\left(x_{i} ; \mu\right)=(2 \pi)^{-\frac{n}{2}} \exp \left[-\frac{1}{2} \sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2}\right]$.
• 似然比 $l\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\exp \left[n\left(\mu_{1}-\mu_{0}\right) \overline{x}-\frac{n}{2}\left(\mu_{1}^{2}-\mu_{0}^{2}\right)\right]$.
• 由 Neyman-Pearson 定理，最大功效检验的拒绝域形如
  
  • $W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | l\left(x_{1}, x_{2}, \cdots, x_{n}\right)>k\right\}$
    
    • $=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \overline{x}>k_{1}\right\}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \sqrt{n}\left(\overline{x}-\mu_{0}\right)>k_{0}\right\}$
  • 其中 $k_{1}=\left[\ln k+\frac{n}{2}\left(\mu_{1}^{2}-\mu_{0}^{2}\right)\right] / n\left(\mu_{1}-\mu_{0}\right)$, $k_{0}=\sqrt{n}\left(k_{1}-\mu_{0}\right)$.

---

• $H_0$ 成立时，$\sqrt{n}\left(\overline{X}-\mu_{0}\right) \sim N(0 ; 1)$.
• 取临界值 $k_0=u_{1-\alpha}$，使得 $P_{\mu_{0}}\left\{\sqrt{n}\left(\overline{X}-\mu_{0}\right)>u_{1-a}\right\}=\alpha$.
• 故所求最大功效检验的拒绝域为
  
  • $W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \sqrt{n}\left(\overline{x}-\mu_{0}\right)>u_{1-\alpha}\right\}$.

---

例：求一致最大功效检验

设 $X_1, X_2,\ldots, X_n$ 是取自 $X\sim N (\mu;1)$ 的样本，其中 $\mu$ 未知，证明对于单侧假设检验问题

$$H_0:\mu\leqslant\mu_0,\quad H_1:\mu>\mu_0.$$

前例给出的拒绝域为

$$W_{1}^{*}=\left\{\left(x_{1}, x_{2}, \cdots, x_{n}\right) | \sqrt{n}\left(\overline{x}-\mu_{0}\right)>u_{1-\alpha}\right\}$$

的检验 $\phi^*$ 是显著性水平 $\alpha$ 下的一致最大功效检验(UMPT).

---

证明：

• 由前例：任给 $\mu_1>\mu_0$, 对检验 $\boxed{H_0:\mu=\mu_0,\;H_1:\mu=\mu_1}$，$\phi^*$ 是显著性水平 $\alpha$ 的最大功效检验（MPT）.
• 由于 $W_1^*$ 与 $\mu_1$ 的取值无关，所以对于检验 $\boxed{H_0:\mu=\mu_0,\;H_1:\mu>\mu_0}$， $\phi^*$ 是显著性水平 $\alpha$ 下的一致最大功效检验（UMPT）.
• 设 $\phi$ 是 $\boxed{H_0:\mu\leqslant\mu_0,\; H_1:\mu>\mu_0}$ 在显著性水平 $\alpha$ 下的任意一个检验，拒绝域为 $W_1$. 即：当 $\mu\leqslant\mu_0$ 时，$P_{\mu}\left\{\left(X_{1}, X_{2}, \cdots, X_{n}\right) \in W_{1}\right\} \leqslant \alpha$.
• 因而 $\phi$ 也是 $\boxed{H_0:\mu=\mu_0,\;H_1:\mu>\mu_0}$ 在显著性水平 $\alpha$ 下的一个检验.

---

• 因为 $\phi^*$ 是检验问题 $\boxed{H_0:\mu=\mu_0,\;H_1:\mu>\mu_0}$ 的 UMPT, 故当$\mu>\mu_0$ 时，必有 $\beta_{\phi^*}(\mu) \geqslant \beta_{\phi}(\mu)$.
• 可以验证 $\phi^*$ 是原假设问题的在显著性水平 $\alpha$ 下的一个检验.

• 综上，$\phi^*$ 是原假设检验问题的 UMPT.

• 注：

  • N-P 引理为构造 UMPT 提供了基本的思路.
  • 可以类似地证明，本课程中仅含一个总体参数的单侧检验都是 UMPT.
  • 求 UMPT，一般来说是很困难的，而且有时 UMPT 不存在.

---

The scientist only imposes two things, namely truth and sincerity, imposes them upon himself and upon other scientists.
--Erwin Schrödinger