第二十三讲 区间估计

概率论与数理统计 讲义 NUDT 2023SP

---

---

23.1 区间估计的基本概念

• 在很多实际问题中，为了作出某种推断，人们更关心某个参数的取值范围，而不需要特别强调参数的精确值.
  
  • 有时候确定估值的可靠性比讨论具体的估值更重要.
• 点估计： 对参数取值给出直接的估计.
• 区间估计： 给出参数的某个取值区间 (置信区间，confidence interval) 以及其真值落在该区间内的概率 (置信水平，confidence level)，从而帮助形成某种统计推断.

---

置信区间

设 $X_1,X_2,...,X_n$ 是来自某个总体的样本，分布函数为 $F(x;\theta)$，其中 $\theta$ 未知.

给定 $\alpha\in(0,1)$，若存在统计量 $\overline{\theta}$ 和 $\underline{\theta}$, 使得

$$\bbox[yellow]{P\left\{\underline{\theta}<\theta<\overline{\theta}\right\}\geq 1-\alpha,}$$

则称区间 $\left(\underline{\theta},\overline{\theta}\right)$ 为参数 $\theta$ 的一个 $1-\alpha$ (双侧)置信区间，$\overline{\theta},\underline{\theta}$ 分别称为 $\theta$ 的 双侧置信上、下限.

---

单侧置信区间

给定 $\alpha\in(0,1)$, 若存在统计量 $\overline{\theta}$, 使得

$$\bbox[yellow]{P\left\{\theta<\overline{\theta}\right\}\geq 1-\alpha,}$$

则称区间 $\left(-\infty,\overline{\theta}\right)$ 为参数 $\theta$ 的一个 $1-\alpha$ 单侧置信区间，$\overline{\theta}$ 称为 $\theta$ 的 单侧置信上限.

• 同理可以定义 $\theta$ 的单侧置信下限.

---

例：理想的键盘高度

人机工程学设计师希望设计出一款工作效率和舒适度最理想的键盘. 为此，他们将关注的重点放在了键盘托架的高度上. 为了得到最理想的高度范围，设计师邀请了 31 位熟练的打字员，分别获取了对他们来说最为理想的托架高度. 结果得到的平均值为 $\overline{x}=80.0$ cm. 假设打字员所钟意的托架高度服从方差为 4 均值为 $\mu$ 的正态分布. 试给出 $\mu$ 的一个 $0.95$ 置信区间.

---

分析：

• 设 $X_1,X_2,...,X_n$ 为来自总体 $N(\mu,\sigma^2)$ 的样本.
• 于是 $\overline{X}\sim N\left(\mu,\displaystyle \frac{\sigma^2}{n}\right)$, 进而 $Z=\displaystyle \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$.
• $P\left\{u_{\alpha/2}<\displaystyle \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}< u_{1-\alpha/2}\right\}=1-\alpha$.
• 即 $P\left\{\displaystyle \overline{X}+u_{\alpha/2}\frac{\sigma}{\sqrt{n}}<\mu<\overline{X}+u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right\}=1-\alpha$.
• 代入本例中的数值计算，可得 $(79.3,80.7)$ 是 $\mu$ 的一个 $0.95$ 置信区间.

---

置信区间的含义

上面的例子中，

• 因为 $\mu$ 是一个常数（但取值未知），以上求得的置信区间的意义并不能理解为 $P\{\mu\in(79.3,80.7)\}=0.95$.
• 而只能理解为置信区间 $\left(\overline{X}-1.96\displaystyle \frac{\sigma}{\sqrt{n}},\overline{X}+1.96\frac{\sigma}{\sqrt{n}}\right)$ 中包含 $\mu$ 的概率为 $0.95$.

---

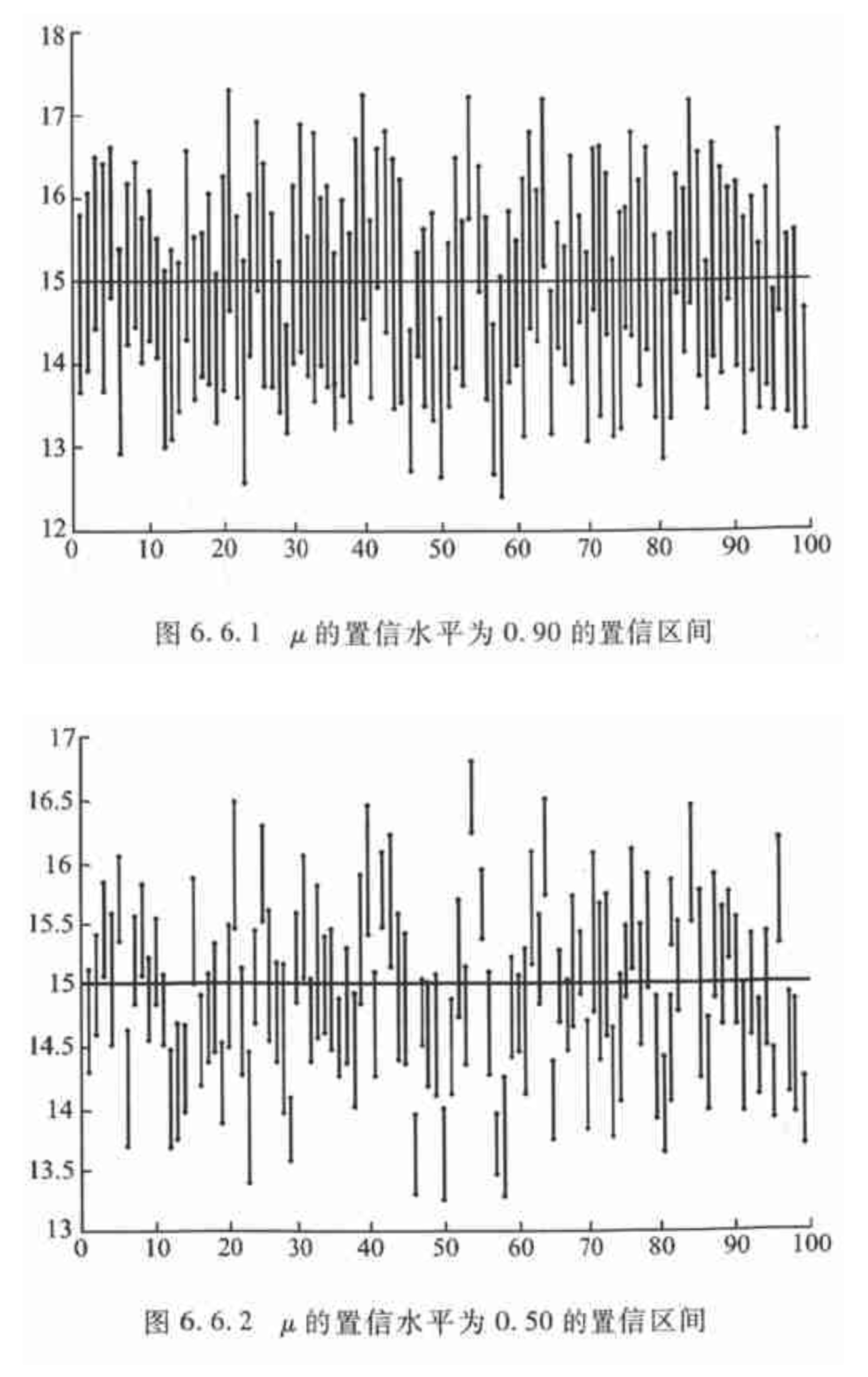
置信区间不具有唯一性

前例中，$\mu$ 的 $1-\alpha$ 置信区间为

$$\left(\overline{x}+u_{\alpha/2}\frac{\sigma}{\sqrt{n}},\overline{x}+u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right)$$

• 为了方便，可以简写为 $\displaystyle \bbox[yellow]{\overline{x}\pm u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}.}$
• 显然，置信区间并不具有唯一性，也不一定要求两侧具有对称性.
• 例如：$\displaystyle \left(\overline{x}+u_{\frac{1}{3}\alpha}\frac{\sigma}{\sqrt{n}},\overline{x}+u_{1-\frac{2}{3}\alpha}\frac{\sigma}{\sqrt{n}}\right)$ 也是一个满足要求的置信区间.

---

例：双侧置信区间的宽度

• 某计算机系统上特定的编辑指令的响应时间服从标准差为 25 毫秒的正态分布.
• 安装新的操作系统后，希望对其平均响应时间的均值 $\mu$ 重新进行估计.
• 假设安装新的操作系统后，响应时间仍服从正态分布，且标准差不变.
• 为了使得 $\mu$ 的 $0.95$ 置信区间宽度不超过 10，样本的容量至少要有多大？

---

分析： 参考前例，置信区间为 $\overline{x}\mp 2u_{0.975}\frac{\sigma}{\sqrt{n}}$，依题意须满足

$$2(u_{0.975})\frac{\sigma}{\sqrt{n}}\leq 10,$$

即 $\displaystyle \sqrt{n}\geq 2(1.96)\frac{25}{10}=9.8$，故 $n\geq (9.8)^2=96.04$.

• 注: 在样本容量不变的前提下，如果提高置信水平，置信区间的宽度将会增加. 此时，可以说：估计的可靠性 (reliability) 提高了，但估计的精度 (precision) 有所下降.

---

枢轴变量

设 $X_1,X_2,...,X_n$ 为对未知参数 $\theta$ 进行区间估计所需的样本. 所谓枢轴变量 (pivotal quantity) $T$，是指：

1. $T$ 是 $X_1,X_2,...,X_n$ 和 $\theta$ 的函数.
   
   • $T$ 不是统计量.

2. $T$ 的分布与 $\theta$ 或其他的任何未知参数均无关.

   • 无论 $\theta$ 如何取值，$T$ 的分布不变.

   • 利用枢轴变量推导参数置信区间的方法称为枢轴变量法.

---

用枢轴变量法求置信区间

1. 构造样本的函数 $g\left(X_{1},\cdots, X_{n} ; \theta\right)$，也即 枢轴变量 (Pivotal Quantity).
2. 对置信度 $1-\alpha$，确定 $g\left(X_{1}, \cdots, X_{n} ; \theta\right)$ 的分布的两个分位点 $\eta_{\alpha/2}$ 和 $\eta_{1-\alpha/2}$, 使得 $\bbox[yellow]{P\left\{\eta_{\alpha / 2}< g< \eta_{1-\alpha / 2}\right\}=1-\alpha.}$
   
   • 注： 在没有事先声明的情况下，默认地按以上方式取两侧的分位点，所得到的的置信区间称为 等尾置信区间.
3. 解不等式 $\eta_{\alpha / 2}< g\left(X_{1}, \cdots, X_{n} ; \theta\right)< \eta_{1-\alpha / 2}$, 得到置信区间：$\left(\underline{\theta}, \overline{\theta}\right)$.

---

Jerzy Neyman (1894-1981)

• Polish mathematician and statistician
• Neyman first introduced the modern concept of a confidence interval into statistical hypothesis testing
• and co-revised Ronald Fisher's null hypothesis testing (in collaboration with Egon Pearson).

---

例：理想的键盘高度

已知 $\overline{x}=80.0$, 理想高度服从 $\sigma=2.0$ 的正态分布，求 $\mu$ 的 $0.95$ 置信区间.

• 枢轴变量：$Z=\displaystyle \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$.
• 思考: 如果本例中 $\sigma$ 也是未知的，以上的 $Z$ 还是枢轴变量吗？
  
  1. 如果不是，应该如何定义枢轴变量？
  2. 枢轴变量的选择是唯一的吗？

---

23.2 单个正态总体的区间估计

已知 $X_1,X_2,...,X_n$ 为来自正态总体 $N(\mu,\sigma^2)$ 的样本, 分别考虑如下四个区间估计问题:

1. $\sigma^2$ 已知，求 $\mu$ 的置信区间.
2. $\sigma^2$ 未知，求 $\mu$ 的置信区间.
3. $\mu$ 已知，求 $\sigma^2$ 的置信区间.
4. $\mu$ 未知，求 $\sigma^2$ 的置信区间.

---

单正态总体的 $1-\alpha$ 置信区间

$$\begin{array}{c|c|c|c|c|c} \hline \text{待估参数} & \text{条件} & \text{枢轴变量} & \text{分布} & \text{双侧置信区间下、上限} & \text{单侧置信下、上限}\\[1em] \hline \mu & \sigma^2\text{已知} & \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} & N(0,1) & \overline{x}\mp u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} & \overline{x}\mp u_{1-\alpha}\frac{\sigma}{\sqrt{n}}\\[1em] \hline \mu & \sigma^2\text{未知} & \frac{\overline{X}-\mu}{S/\sqrt{n}} & t(n-1) & \overline{x}\mp t_{1-\alpha/2}(n-1)\frac{s}{\sqrt{n}} & \overline{x}\mp t_{1-\alpha}(n-1)\frac{s}{\sqrt{n}}\\[1em] \hline \sigma^2 & \mu\text{已知} & \sum\limits_{i=1}^n\left(\frac{X_i-\mu}{\sigma}\right)^2 & \chi^2(n) & \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{1-\alpha/2}(n)},\; \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{\alpha/2}(n)} & \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{1-\alpha}(n)},\; \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{\alpha}(n)}\\[1em] \hline \sigma^2 & \mu\text{未知} & \sum\limits_{i=1}^n\left(\frac{X_i-\overline{X}}{\sigma}\right)^2 & \chi^2(n-1) & \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{1-\alpha/2}(n-1)},\; \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{\alpha/2}(n-1)} & \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{1-\alpha}(n-1)},\; \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{\alpha}(n-1)}\\ \hline \end{array}$$

---

提示： 求 $\sigma^2$ 的 $1-\alpha$ 置信区间（假设 $\mu$ 已知）

1. 求双侧置信区间

• 枢轴变量 $\chi^2=\sum\limits_{i=1}^n\left(\frac{X_i-\mu}{\sigma}\right)^2\sim\chi^2(n)$.
• 设 $P\left\{C_1\leq\sigma^2\leq C_2\right\}=1-\alpha$，也即
  
  • $P\left\{\frac{1}{C_2}\sum\limits_{i=1}^n(X_i-\mu)^2\leq\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2\leq \frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2\right\}=1-\alpha$.
• 取 $\frac{1}{C_2}\sum\limits_{i=1}^n(X_i-\mu)^2=\chi^2_{\alpha/2}(n)$，$\frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2=\chi^2_{1-\alpha/2}(n)$.
• 解得 $C_1=\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{1-\alpha/2}(n)}$，$C_2=\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{\alpha/2}(n)}$.

---

2. 求单侧置信下限

• 枢轴变量 $\chi^2=\sum\limits_{i=1}^n\left(\frac{X_i-\mu}{\sigma}\right)^2\sim\chi^2(n)$.
• 设 $P\left\{C_1\leq\sigma^2\right\}=1-\alpha$，也即
  
  • $P\left\{\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2\leq \frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2\right\}=1-\alpha$.
• 取 $\frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2=\chi^2_{1-\alpha}(n)$，解得 $C_1=\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{1-\alpha}(n)}$.

---

例：灯泡的寿命

从灯泡厂随机抽取 $10$ 只灯泡，进行寿命试验，测得数据如下（单位：小时）

$$1050,1100,1080,1120,1200,1250,1040,1130,1300,1200.$$

设灯泡寿命服从正态分布，给出这批灯泡的平均寿命及方差的置信度为 $95\%$ 的置信区间.

---

解：

• 设 $X$ 为灯泡的寿命，设 $X\sim N(\mu,\sigma^2)$，其中 $\mu,\sigma^2$ 均未知.
• $\mu$ 的置信度为 $1-\alpha$ 置信区间是 $\left(\bar{x} \mp t_{1-\alpha / 2}(n-1) \dfrac{s}{\sqrt{n}}\right)$.
• 利用抽样数据进行计算，$\overline{x}=\frac{1}{10}(1050+\cdots+1200)=1147$.
  
  • $s=\sqrt{\frac{1}{9} \sum_{i=1}^{10}\left(x_{i}-\bar{x}\right)^{2}}=\sqrt{\frac{1}{9} \sum_{i=1}^{10}\left(x_{i}-1147\right)^{2}}=82.59$.
• 查表 $t_{1-\alpha / 2}(n-1)=t_{0.975}(9)=2.26$，故 $\mu$ 的置信度为 $95\%$ 的置信区间为 $\left(1147 \mp 2.26 \times \frac{82.59}{\sqrt{9}}\right)=(1084.78,1209.22)$.

---

• $\sigma^2$ 的置信度为 $1-\alpha$ 的置信区间为 $\left(\dfrac{(n-1) s^{2}}{\chi_{1-\alpha / 2}^{2}(n-1)}, \dfrac{(n-1) s^{2}}{\chi_{\alpha / 2}^{2}(n-1)}\right)$.
• $s^{2}=82.59^{2}=6821.10$.
• $\chi_{\alpha / 2}^{2}(n-1)=\chi_{0.025}^{2}(9)=2.7$.
• $\chi_{1-\alpha / 2}^{2}(n-1)=\chi_{0.975}^{2}(9)=19.023$.
• $\sigma^2$ 的置信度为 $95\%$ 的置信区间为 $\left(\frac{9 \times 6821.10}{19.023}, \frac{9 \times 6821.10}{2.7}\right)=(3585.71,25263.33).$

---

23.3 双正态总体的区间估计

• 设 $X_1,X_2,...,X_m$ 和 $Y_1,Y_2,\ldots,Y_n$ 分别为来自 $N(\mu_1,\sigma_1^2)$ 和 $N(\mu_2,\sigma_2^2)$ 的样本，且二者相互独立.
• 试对其均值的差 $\mu_1-\mu_2$ 和方差的比值 $\displaystyle \frac{\sigma_1^2}{\sigma_2^2}$ 给出区间估计.

---

双正态总体的 $1-\alpha$ 置信区间

$$\boxed{\begin{array}{c|c|c|c|c} \text{待估参数} & \text{条件} & \text{枢轴变量及其分布} & \text{双侧置信区间下、上限} & \text{单侧置信下、上限}\\[1em] \hline \mu_1-\mu_2 & \sigma_1^2,\sigma_2^2\text{已知} & \frac{\displaystyle \overline{X}-\overline{Y}-(\mu_1-\mu_2)}{\sqrt{\displaystyle \frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}} \sim N(0,1) & (\overline{x}-\overline{y})\mp u_{1-\alpha/2}\sqrt{\displaystyle \frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}} & (\overline{x}-\overline{y})\mp u_{1-\alpha}\sqrt{\displaystyle \frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}\\[1em] \hline \mu_1-\mu_2 & \sigma_1^2=\sigma_2^2=\sigma^2\text{未知} & \displaystyle \frac{\displaystyle \overline{X}-\overline{Y}-(\mu_1-\mu_2)}{S_{\omega}\sqrt{\displaystyle \frac{1}{m}+\frac{1}{n}}} \sim t(m+n-2) & \displaystyle \overline{x}-\overline{y}\mp t_{1-\alpha/2}(m+n-2){s_{\omega}\sqrt{\displaystyle \frac{1}{m}+\frac{1}{n}}} & \displaystyle \overline{x}-\overline{y}\mp t_{1-\alpha}(m+n-2){s_{\omega}\sqrt{\displaystyle \frac{1}{m}+\frac{1}{n}}}\\[1em] \hline \sigma_1^2/\sigma_2^2 & \mu_1,\mu_2\text{已知} & \frac{\displaystyle\frac{1}{m} \sum\limits_{i=1}^m\left(\frac{X_i-\mu_1}{\sigma_1}\right)^2}{\displaystyle \frac{1}{n}\sum\limits_{i=1}^n\left(\frac{Y_i-\mu_2}{\sigma_2}\right)^2} \sim F(m,n) & \begin{array}{c}\frac{\frac{1}{m}\sum\limits_{i=1}^m(x_i-\mu_1)^2}{\frac{1}{n}\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{1-\alpha/2}(m,n)}\\ \frac{\frac{1}{m}\sum\limits_{i=1}^m(x_i-\mu_1)^2}{\frac{1}{n}\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{\alpha/2}(m,n)}\end{array} & \begin{array}{c}\frac{\frac{1}{m}\sum\limits_{i=1}^m(x_i-\mu_1)^2}{\frac{1}{n}\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{1-\alpha}(m,n)}\\ \frac{\frac{1}{m}\sum\limits_{i=1}^m(x_i-\mu_1)^2}{\frac{1}{n}\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{\alpha}(m,n)}\end{array} \\[1em] \hline \sigma_1^2/\sigma_2^2 & \mu_1,\mu_2\text{未知} & \displaystyle \frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2} \sim F(m-1,n-1) & \begin{array}{c}\frac{s_1^2}{s_2^2}\frac{1}{F_{1-\alpha/2}(m-1,n-1)}\\ \frac{s_1^2}{s_2^2}\frac{1}{F_{1-\alpha/2}(m-1,n-1)}\end{array} & \begin{array}{c}\frac{s_1^2}{s_2^2}\frac{1}{F_{\alpha}(m-1,n-1)}\\ \frac{s_1^2}{s_2^2}\frac{1}{F_{\alpha}(m-1,n-1)}\end{array} \end{array}}$$

---

例：比较子弹的初速度

为了比较两类子弹的初速度，进行了如下的抽样试验. 任取 10 发 A 类子弹，测得其平均初速度及其标准差分别为 $\overline{x}_1=500$(m/s) 和 $s_1=1.10$(m/s)；任取 20 发 B 类子弹，测得其平均初速度及其标准差分别为 $\overline{x}_2=496$(m/s) 和 $s_2=1.20$(m/s). 假设两类子弹的初速度服从方差相同的正态分布，试求两者均值之差的 $0.95$ 置信区间.

---

解：

• 由实际情况，可认为分别来自两个总体的样本是相互独立的.
• 由于它们的方差相等且未知，故 $\mu_1-\mu_2$ 的置信度 $1-\alpha$ 的置信区间为 $\left((\overline{x}-\overline{y}) \pm t_{1-\alpha / 2}(m+n-2) s_{\omega} \sqrt{\frac{1}{m}+\frac{1}{n}}\right)$.
• 其中 $1-\alpha=0.95$, $t_{0.975}(28)=2.0484$, $s_{\omega}=\sqrt{\frac{9 \times 1.10^{2}+19 \times 1.20^{2}}{28}}=1.1688$.
• 故 $\mu_1-\mu_2$ 的置信度为 $0.95$ 的置信区间为 $(4 \pm 0.93)=(3.07,4.93)$.

---

The whole of science is nothing more than a refinement of everyday thinking.
--Albert Einstein

---

例：飞机的飞行高度

为了提高可靠性和测量精度，飞机通常安装了若干个高度仪. 设飞机实际飞行高度为 $\mu$ 时每个高度仪测量值 $X\sim N(\mu,64)$，而飞机仪表上显示的飞行高度是所有的高度测量值的平均值. 在置信水平 $1-\alpha=0.98$ 下，求解下列问题：

1. 若要保证飞行仪表上显示的飞信高度的绝对误差不超过 $12$ m，问飞机上至少安装多少个高度仪？
2. 若飞机装有 $4$ 个高度仪，飞行仪表上显示的飞行高度是 $9813$ m，问飞机实际飞行在什么高度范围？

---

提示：

• 1. 假设有 $n$ 个高度仪，高度测量值分别为 $X_1,X_2,...,X_n$，则 $\overline{X}\sim N\left(\mu,\frac{64}{n}\right)$.
• 问题等价于，要使 $P\left\{|\overline{X}-\mu|< 12\right\}\geq 0.98$，$n$ 至少需要取多大？
• 上式也即 $P\left\{\frac{-12}{8/\sqrt{n}}< \frac{\overline{X}-\mu}{8/\sqrt{n}}<\frac{12}{8/\sqrt{n}}\right\}\geq 0.98$.
• 由此可得 $\frac{12}{8/\sqrt{n}}\geq u_{1-\frac{\alpha}{2}}=u_{0.99}$，即 $n\geq 64\cdot\frac{u_{0.99}^2}{144}\approx 2.41$.
• 结论：安装至少 $3$ 个高度仪就可以满足要求.

---

• 1. 此时 $\overline{X}\sim N(\mu,16)$，进而 $\frac{\overline{X}-\mu}{4}\sim N(0,1)$.
• $P\left\{u_{0.01}< \frac{\overline{X}-\mu}{4}< u_{0.99}\right\}\geq 0.98$.
• 故 $\mu\in(\overline{x}-u_{0.99}\cdot 4,\overline{x}-u_{0.99}\cdot 4)\approx(\overline{x}-9.32,\overline{x}+9.32).$
• 已知 $\overline{x}=9813$，故此时飞机的实际高度范围为 $(9803.68,9822.32)$.
• 思考： 真的可以确定飞机在以上的高度范围内飞行吗？