第七讲 离散型随机变量的期望与方差

概率论与数理统计 讲义 NUDT 2023SP

---

---

7.1 随机变量的期望

例： 一所大学共有 15,000 名学生，下表是按照选课门数对人数进行的统计，求平均每个学生选修的课程门数.

$$\begin{array}{c|ccccccc|c} \text{选课门数} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \text{合计}\\ \hline \text{人数} & 150 & 450 & 1950 & 3750 & 5850 & 2550 & 300 & 15000 \end{array}$$

• $\text{平均选课门数}=\frac{1\times150+2\times450+\ldots+7\times300}{15000}=4.57$

---

例：随机变量取值的平均

例：一所大学共有 15,000 名学生，随机变量 $X$ 表示任意一个学生注册的课程门数. $X$ 的 pmf 如下表所示. 求 $X$ 的平均值.

$$\begin{array}{c|ccccccc|c} \text{选课门数 }x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \text{合计}\\ \hline \text{人数} & 150 & 450 & 1950 & 3750 & 5850 & 2550 & 300 & 15000\\ \text{人数比例 }p(x) & 0.01 & 0.03 & 0.13 & 0.25 & 0.39 & 0.17 & 0.02 & 1 \end{array}$$

• $\text{平均选课门数}=1\times p(1)+2\times p(2)+\ldots+7\times p(7)=4.57$.
• 以上的均值也可以理解为 $X$ 最有可能取到的值 (的近似)，称为 随机变量 $X$ 的期望值 (Expected Value).
• 记为：$\bbox[yellow]{E(X)}$, $EX$, $\mu_X$, $\mu$.

---

离散型随机变量的期望

设 $X$ 是离散型随机变量，取值范围 $D$，pmf 为 $p(x)$. 则其 期望值 (简称：期望) or 均值(Mean value)

$E(X)=\sum\limits_{x\in D}x\cdot p(x)$

• 记 $D=\{x_1,x_2,...\}$ 且 $p_k=P\{X=x_k\}$, 则
  
  • $E(X)=\sum\limits_{k=1}^{\infty}x_k\cdot p_k$

---

期望的意义

• $E(X)$ 本质上是对 $X$ 的所有可能取值的一个加权平均 (weighted average).
• $E(X)$ 有时并不是 $X$ 的一个可能取值, 但却是总体上最接近于 $X$ 的所有可能的取值的值.
• $E(X)$ 也可以理解为大量重复试验情况下，$X$ 的取值的总的平均，或对可能观测到的所有结果的最好的近似.

---

例：民意调查

rv $X=$ 投票选项对应的数值.

$$\begin{aligned} E(X)=&1\times 0.05+2\times 0.68\\ &+3\times 0.21 + 4\times 0.04\\ &+5\times 0.02\\ = & 2.3 \end{aligned}$$

• 以上结果反映出，总体上，本班同学认为概率论比微积分要容易学.

---

Bernoulli rv 的期望值

已知 $X$ 为Bernoulli rv, 其 pmf

$$p(x)=\left\{\begin{array}{cl}\alpha & x=1\\ 1-\alpha & x=0\end{array}\right.$$

其中 $0<\alpha<1$.

• $E(X)=1\times \alpha+0\times(1-\alpha)=\alpha$
• 例： 以 rv $X=0,1$ 分别代表硬币的两面.
  
  • $E(X)=0\times 0.5+1\times 0.5=0.5.$

---

例：节约检验费用的方案

• 在某个社区中开展某类病毒的排查，若每个人分别采样化验，则一个人消耗一份化验费.
• 为了节省费用，采用一种改进的方案：将 $k$ 个人的样本混合在一起化验.
• 如果呈阴性，则说明每个人都没有问题. 否则，则将以上的 $k$ 个人再次全部分别进行检验.
• 已知当前病毒总体的感染率为 $q$.
• 问：如何优化以上方案，使得总体的检验费用尽可能地少？

---

分析： 记 $X$ 为每个人产生的检验费用.

• 于是 $X\sim\begin{pmatrix} 1/k & 1+1/k\\ (1-q)^k & 1-(1-q)^k \end{pmatrix}$.
• $E(X)=\frac{1}{k}(1-q)^k+\left(1+\frac{1}{k}\right)[1-(1-q)^k]=1+\frac{1}{k}-(1-q)^k.$
• 以单人检验费用的期望最小化为目标，寻找最优的 $k$，就能够使得检验的费用总体上尽可能地少.
• 例如：$q=0.001$，$k=10$，$E(X)\approx 0.109955$.

---

例：第一次出现

反复抛一枚图钉. 已知每次针头朝上的概率为$\alpha\;(0<\alpha<1)$，且抛的结果相互独立. 求第一次出现针头朝上时抛的总次数的期望.

---

解： 令 rv $X=$ 第一次出现针头朝上时抛的总次数. $X$ 的 pmf 为

$$p(x)=\left\{\begin{array}{cl}\alpha(1-\alpha)^{x-1} & x=1,2,3,\ldots\\ 0 &\text{其他}\end{array}\right.$$

由定义，$X$ 的期望值为

$$E(X)=\sum\limits_{x=1}^{\infty}x\cdot p(x)=\sum\limits_{x=1}^{\infty}x\cdot \alpha(1-\alpha)^{x-1}=\frac{1}{\alpha}.$$

• 本例中 $X$ 的分布称为 几何分布 (Geometric distribution)，记为 $X\sim GE(\alpha)$

---

注：上例中的无穷和的计算过程，记 $\beta=1-\alpha$，

$$\begin{aligned} \sum\limits_{x=1}^{\infty}&x\cdot \alpha(1-\alpha)^{x-1} = \alpha\sum\limits_{x=1}^{\infty}x\cdot \beta^{x-1}=\alpha\sum\limits_{x=1}^{\infty}\frac{\mathrm{d}}{\mathrm{d}\beta}\beta^{x}\\ &=\alpha\frac{\mathrm{d}}{\mathrm{d}\beta}\sum\limits_{x=1}^{\infty}\beta^{x}=\alpha\frac{\mathrm{d}}{\mathrm{d}\beta}\left(\frac{1}{1-\beta}-1\right)=\alpha\frac{1}{(1-\beta)^2}=\frac{1}{\alpha} \end{aligned}$$

---

期望的存在性

例: 设 $X$ 的 pmf 为

$$P\{X=k\}=\frac{6}{\pi^2k^2},\quad k=1,2,3,\ldots,$$

• $\displaystyle E(X)=\sum\limits_{k=1}^{\infty}k\cdot \frac{6}{\pi^2k^2}=\sum\limits_{k=1}^{\infty}\frac{6}{\pi^2k}=\infty$
• 定理： 设 rv $X\in D$ 且 pmf 为 $p(x)$，若 $\sum\limits_{x\in D}|x|\cdot p(x)$ 收敛，则 $E(X)$ 存在.
  
  • 若 $\sum\limits_{x\in D}|x|\cdot p(x)$ 发散，则称 $X$ 的期望不存在

注：关于以上涉及的级数求和，参考：https://www.cnblogs.com/misaka01034/p/BaselProof.html

---

7.2 随机变量函数的期望

例： 机动车测试的成本与车辆的气缸数 $X$ 紧密相关. 已知 $X$ 的 pmf 如下：

$$\begin{pmatrix} 4 & 6 & 8 \\ 0.5 & 0.3 & 0.2 \end{pmatrix},$$

测试成本 $h(X)=20+3X+0.5X^2$. 由于 $X$ 是一个随机变量，$Y=h(X)$ 必然也是. 试求 $Y$ 的期望值.

---

解： 利用 $X$ 的 pmf 可以导出 $Y$ 的 pmf：

$$\begin{pmatrix} 40 & 56 & 76 \\ 0.5 & 0.3 & 0.2 \end{pmatrix}$$

于是

$$E(Y)=40\times0.5+56\times0.3+76\times0.2=52.$$

• 思考： $E[h(X)]=h[E(X)]$ 是否成立?
• 定理： 设离散型 rv $X\in D$ 的 pmf 为 $p(x)$, 则函数 $h(X)$ 的期望 $E[h(X)]=\sum\limits_{x\in D}h(x)\cdot p(x)$

---

期望的性质

定理：对任意离散型 rv $X$ 和常数 $a,b$

$$E(aX+b)=a\cdot E(X)+b$$

• 推论：对任意常数 $c$, $E(c)=c$.
• 思考： $E\{...E[E(X)]\}=?$
  
  • $E(X)$ 若存在，则为常数.
  • $E\{...E[E(X)]\}=E(X)$.

---

7.3 离散型随机变量的方差

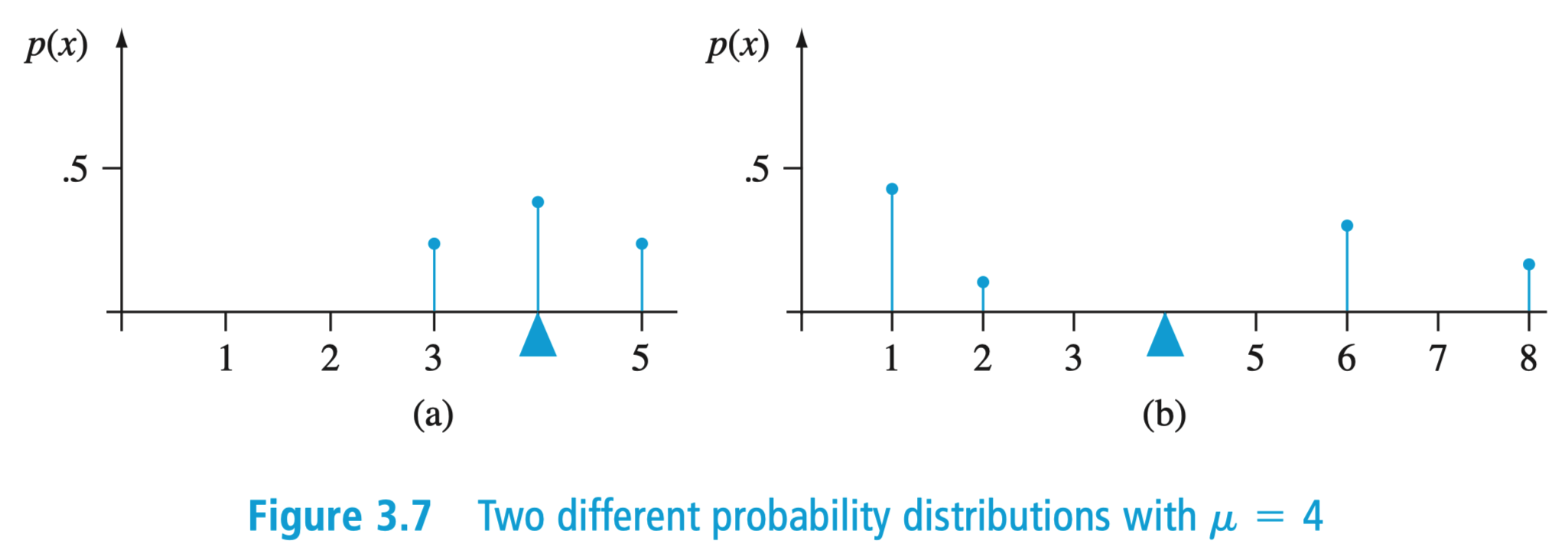
如果两组数据均值相同，还可以如何对进行比较？

---

方差的定义

设离散型 rv $X$ 的 pmf 为 $p(x)$ 且期望值存在 $E(X)$, 则

$$D(X)=E[(X-E(X))^2]$$

称为 $X$ 的 方差(variance)

• 常用记号：$D(X)$, $Var(X)$, $V(X)$, $\sigma^2_X$, $\sigma^2$
• $\sigma=\sqrt{D(X)}$ 称为 $X$ 的标准差(standard deviation).

---

方差的计算

定理： 对离散型 rv $X$, 如果 $E(X)$ 和 $E(X^2)$ 均存在，则

$$D(X)=E(X^2)-[E(X)]^2$$

---

例： 给定离散型 rv $X$ 的 pmf 如下

$$X\sim\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 0.3 & 0.25 & 0.15 & 0.05 & 0.1 & 0.15 \end{pmatrix}$$

• $E(X)=\sum\limits_{x=1}^6x\cdot p(x)=2.85$
• $E(X^2)=\sum\limits_{x=1}^6x^2\cdot p(x)=11.35$
• $D(X)=E(X^2)-[E(X)]^2=3.2275$
• $\sigma=\sqrt{D(X)}\approx1.8$

---

方差的性质

定理 对任意离散型 rv $X$ 和任意常数 $a,b$

$$D(aX+b)=a^2\cdot D(X)$$

• 推论 对任意常数 $c$, $D(c)=0$.

---

Bernoulli rv 的方差

考虑 Bernoulli rv $X$, 其 pmf 为

$$p(x)=\left\{\begin{array}{ll}\alpha & x=1\\ 1-\alpha & x=0\end{array}\right.$$

其中 $0<\alpha<1$.

• $E(X)=1\times \alpha+0\times(1-\alpha)=\alpha$
• $E(X^2)=1^2\times \alpha+0^2\times(1-\alpha)=\alpha$
• $D(X)=E(X^2)-[E(X)]^2=\alpha-\alpha^2=\alpha(1-\alpha)$

---

小结

• 期望：$E(X)=\sum\limits_xxp(x)$
  
  • rv 的函数的期望：$E(g(X))=\sum\limits_xg(x)p(x)$
  • $E(aX+b)=aE(X)+b$
• 方差：$D(X)=E[(X-E(X))^2]$
  
  • $D(X)=E(X^2)-[E(X)]^2$
  • $D(aX+b)=a^2D(X)$
• 熟练掌握 Bernoulli 分布的 pmf，期望和方差

---

Every good mathematician is at least half a philosopher, and every good philosopher is at least half a mathematician.
-- Friedrich Ludwig Gottlob Frege

---

课堂讨论

如何理解：期望是总体上最接近随机变量所有可能取值的值？

• 定理：
  
  1. $\forall c\in\mathbb{R}$，$D(X)\leq E[(X-c)^2]$.
  2. $c=E(X)$ 是函数 $g(c)=E[(X-c)^2]$ 的唯一最小值点.
  3. 在所有常数中，$E(X)$ 整体上与 $X$ 的所有可能取值最为接近.

---

例：赌场没有福利！

• 有一种赌博游戏的规则如下：顾客押上赌本，并先在 $\{1,2,3,4,5,6\}$ 中选定一个数，然后连续抛掷三次均匀骰子.
• 如果抛掷的点数中有顾客选定的数字，则按照该点数出现的次数，顾客可以在拿回赌本的同时，赢得与次数相同倍数的赌本.
• 如果三次抛掷均未能得到顾客选定的数字，则赌本被庄家（赌场）拿走.
• 顾客在平均意义上是否会赢钱呢？

---

分析： 不妨设顾客选择的数字是 $1$，赌本也是 $1$. $X$ 表示顾客的收益，则 $X\in\{3,2,1,-1\}$.

• $\Omega=\{(x_1,x_2,x_3):x_k\in\{1,2,...,6\},k=1,2,3\}$，$n(\Omega)=216.$
• $P\{X=3\}=P\{(1,1,1)\}=\frac{1}{216}$.
• $P\{X=2\}=P\{(1,1,x),(1,x,1),(x,1,1),x\ne 1\}=\frac{15}{216}$.
• $P\{X=1\}=P\{(1,x,y),(x,1,y),(x,y,1),x,y\ne 1\}=\frac{75}{216}$.
• $P\{X=-1\}=P\{(x,y,z),x,y,z\ne 1\}=\frac{125}{216}$.
• $E(X)=\frac{1}{216}(1\times 3+15\times 2+75\times 1+125\times(-1))=-\frac{17}{216}$

---

矩（Moment）

给定对随机变量 $X$，对任意 $k=1,2,...$，定义

• k 阶原点矩 (k-th origin moment)：$m_k(X)=E(X^k)$
• k 阶中心矩 (k-th centrl moment)：$c_k(X)=E[(X-E(X))^k]$
• 例： $X\sim b(n,p)$
  
  • $m_k(X)=p,\;k=1,2,3,...$
  • $c_3(X)=np(1-p)(1-2p)$, $c_4(X)=np(1-p)[1+(3n-6)p(1-p)]$, ...

---

偏度 (skewness)

$$s(X)=E\left[\left(\frac{X-E(X)}{\sqrt{D(X)}}\right)^3\right]$$

• 用于描述随机变量分布的对称性.
• 偏度为零，说明分布完全左右对称.
• 偏度为正，分布整体的重心偏左；反之偏右.

---

峰度 (kurtosis)

$$k(X)=E\left[\left(\frac{X-E(X)}{\sqrt{D(X)}}\right)^4\right]$$

• 用于描述随机变量峰值的尖锐程度以及拖尾的“粗重”程度.
• 峰度越大，峰值越尖，拖尾越粗；
• 峰度越小，峰值越圆润，拖尾越细.

---

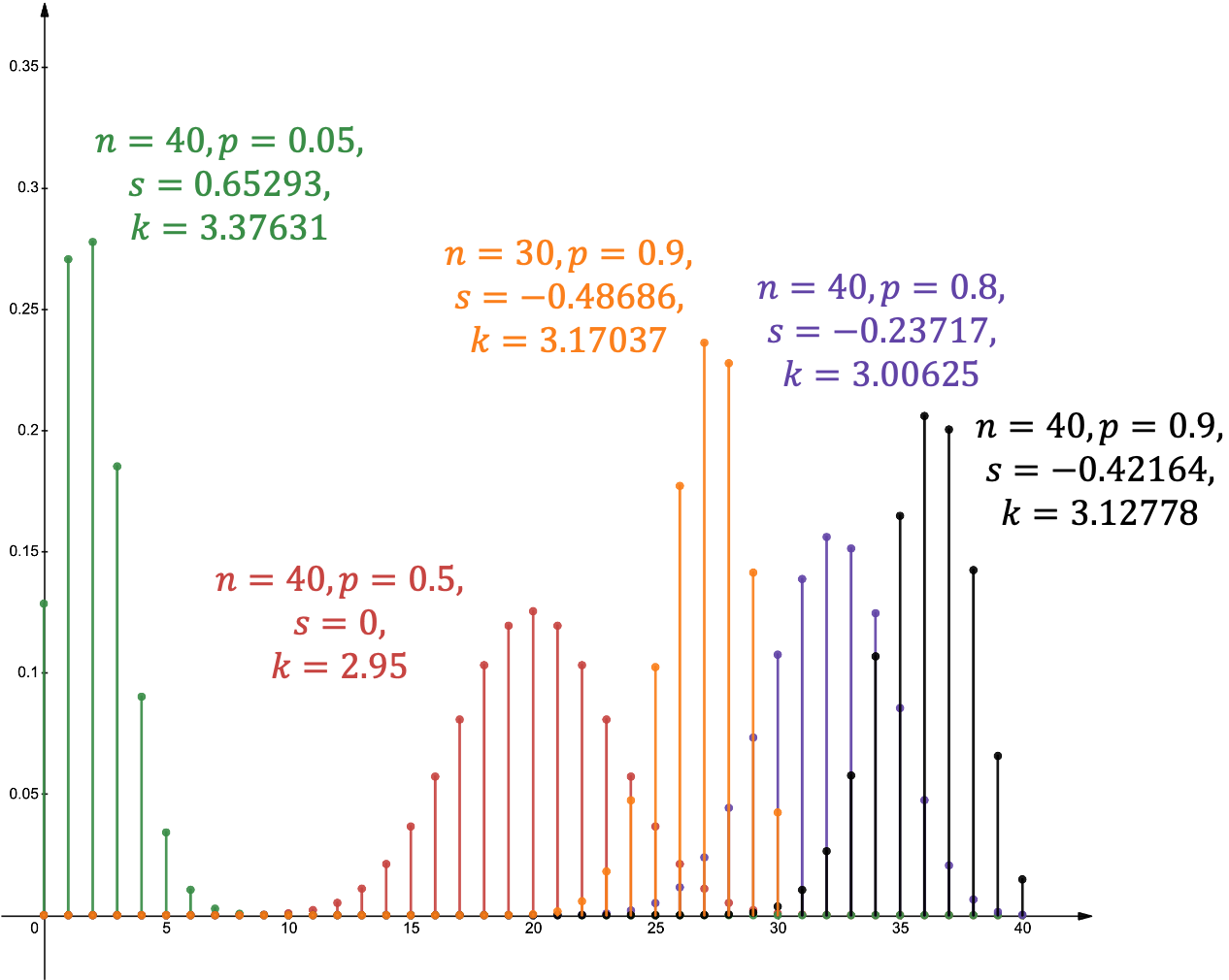
二项分布的偏度与峰度

设 $X\sim b(n,p)$，

• 偏度： $s(X)=\frac{1-2p}{\sqrt{np(1-p)}}$.
• 峰度： $k(X)=\frac{1+(3n-6)p(1-p)}{np(1-p)}$.

---

随机分布的熵

给定离散型随机变量 $X$，满足

$$P\{X=x_k\}=p_k>0,\quad k=1,2,...$$

其 熵 （Entropy）定义为

$$H(X)=-\sum_{k=1}^{\infty}p_k\log_2p_k.$$

• 不难发现，$H(X)>0$，且 $H(X)$ 与 $X$ 的取值无关.
• 熵体现了随机变量的混乱程度，也即随机变量取值的不确定性的大小.

---

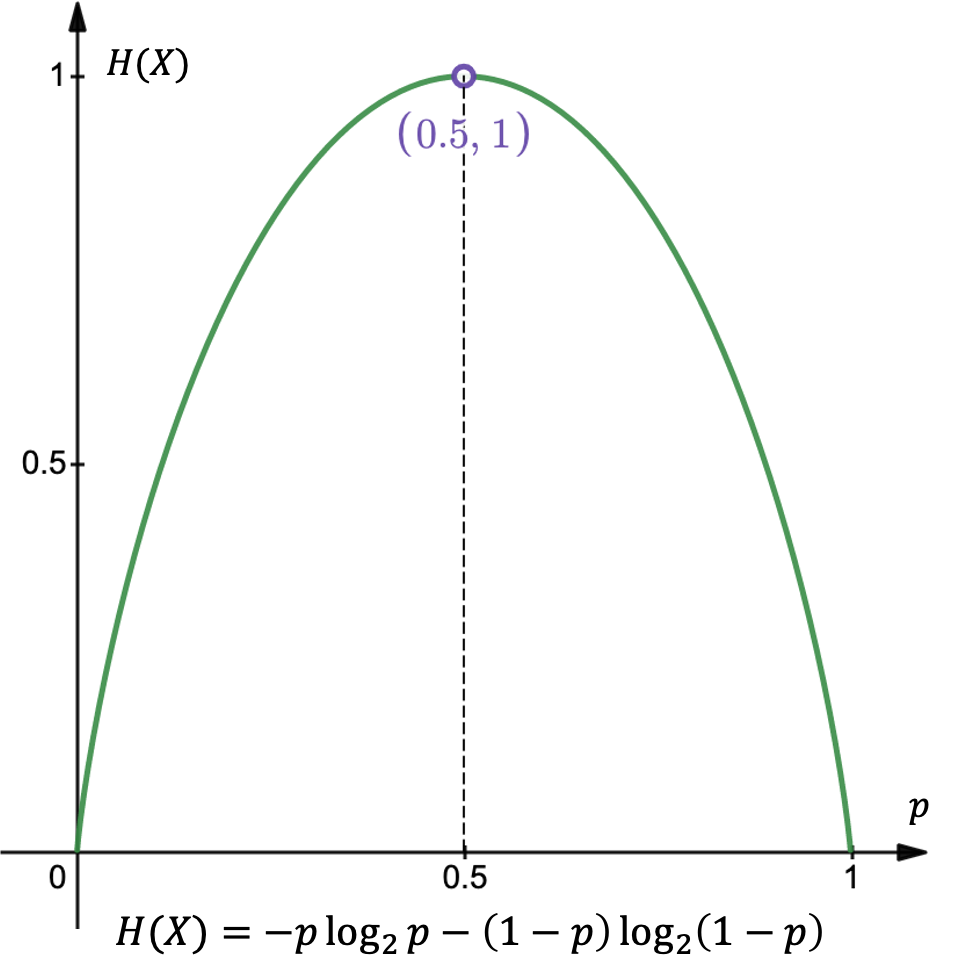
Bernoulli 分布的熵

设 $X\sim b(1,p)$，则

$$H(X)=-p\log_2(p)-(1-p)\log_2(1-p).$$

• 当 $p=1/2$ 时，$H(X)$ 取最大值，也即此时 $X$ 的取值最难以预测.

---

离散均匀分布的熵

定理： 设 $X$ 是仅有有限多个取值的离散型随机变量，则当且仅当 $X$ 的所有取值为等可能时，其熵最大.

• 事实上，对任意有限取值的随机变量，其熵最大为 $\log_2n$.
• 直观地看，均匀分布的随机变量对于任意的取值没有特定的“倾向性”，因此其取值的不确定性最大，也最难以预测.
• 熵常常作为信息量的一种度量，对随机变量而言，一般来说，熵越大则意味着潜在的可能性若多，因此信息量也越大.