@blueband21c
2023-04-19T14:23:47.000000Z
字数 9735
阅读 4532
第十五讲 条件分布与随机变量的独立性
概率论与数理统计 讲义 NUDT 2023SP
回顾:联合分布与边缘分布
15.1 条件分布
设离散型 rv 的联合分布律为 , 的边缘分布律为 .
对任意满足 的 , 可定义 的前提下 的条件分布律 (conditional pmf )
如果 均为连续型 rv,将以上的 pmf 都替换成对应的 pdf,则可定义 的前提下 的条件概率密度 (conditional pdf).
连续型条件概率密度的意义
对连续型 rv ,总有 ,因此条件概率
从数学形式上看是没有意义的.
- 为此,我们转而定义
分析:
条件密度的几何意义
取定 ,等价于取联合密度曲面与平面 的交线.
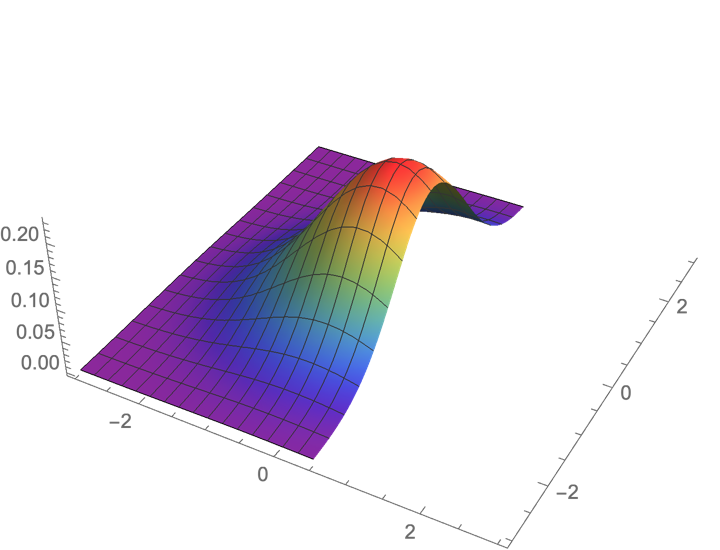
联合密度曲面与平面 的交线,是关于 的函数
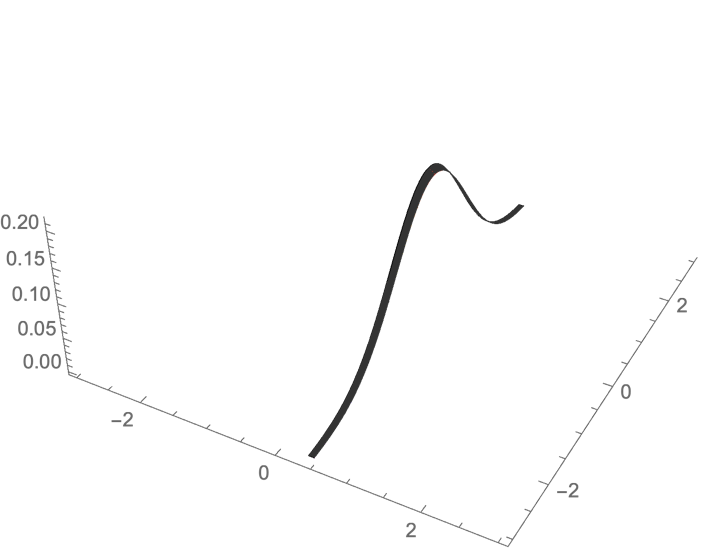
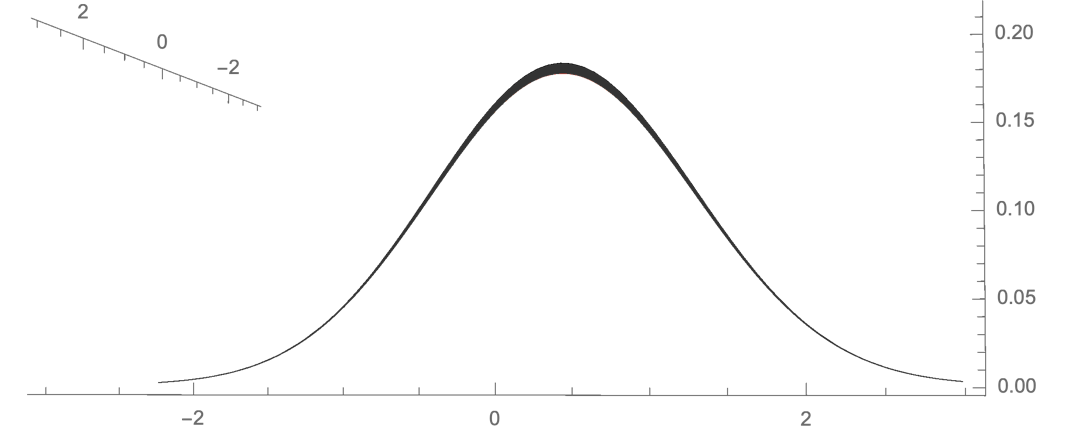
- ,说明函数 不满足 pdf 的本征特性,因此不是一个 pdf.
- 满足 pdf 的本征特性.
例:求离散型随机变量的条件分布律
从 中随机抽取 rv ,然后从 到 的整数中随机抽取 rv ,求 的前提下 的条件分布律.
解:
例:求连续型的条件密度函数
已知随机向量 的密度函数为
求 和 .
- ,
- 当 时,
- 当 时,
15.2 随机变量的独立性
两个随机变量 相互独立(independent) 当且仅当,对任意 , 总有
- **推论:**rv 相互独立,当且仅当:对任意 , 总有
- , 若 均为离散型 rv
- , 若 均为连续型 rv
例:离散型随机变量独立性的判断
- 由以上 pmf 可知,rv 不相互独立.
例:连续型随机变量独立性的判断
已知 rv 的 pdf
判断 是否相互独立.
解:
- 因为对任意 ,, 故可知 相互独立.
随机变量独立性的判断准则
定理: 连续型 rv 相互独立,当且仅当:其联合 pdf 是可分离变量的,即:存在函数 ,使得
- 推广:如果联合 pmf/pdf/cdf 是可分离变量的,则两个随机变量相互独立
例:
- 提示: 记
-
例:设 rv 的 pdf 为
判断 是否相互独立?
提示:
- 注意:仅由 的表达式无法判断其是否是可分离变量的,必须要结合其取值的区域共同考虑!
从边缘分布到联合分布
- 从 的联合分布总是可以得到 的边缘分布.
- 当 相互独立时,由其边缘分布可以唯一确定联合分布.
- 注意: 若 不相互独立,则可以构造出无穷多个不同的联合分布函数 ,使得其对应的边缘分布函数分别为 .
由边缘分布函数“构造”联合分布函数
- 设 的分布函数分别为 .
- 记 ,.
- 满足联合分布函数的本征特性.
15.3 多个随机变量的独立性
设 rv 的 cdf 分别为 . 相互独立,当且仅当:其联合 cdf
随机向量的相互独立性
设随机向量 , 的 cdf 分比为 和 . 与 相互独立,当且仅当:其联合 cdf 为
试验数据的独立性
定理:若随机向量 与 相互独立,则
- 对任意 和 , 与 相互独立.
- 设 分别为 和 元函数,则 与 相互独立.
- 相互独立的两组数据,经过加工(处理)之后仍然相互独立.
例:从不独立到独立
已知 的密度函数
验证: 不相互独立,但 相互独立.
- 注:如果 不相互独立,仍然可以找到函数变换 ,使得 相互独立.
提示:
- ,
- 对任意 ,
-
小结
- 条件分布律与条件密度
- 随机变量相互独立 由二者所定义的所有事件均相互独立
- 联合分布函数/分布律/密度函数是可以分离变量的
The study of mathematics, like the Nile, begins in minuteness but ends in magnificence.
--Charles Caleb Colton
例:圆盘上的均匀分布
随机变量 服从圆盘
上的均匀分布, 试求 ,并判断 是否相互独立.
分析:
- 因此, 当 时,
-
- 综上, 不相互独立!
例:前两次命中的射击次数
- 设某个战士的射击命中率为 .
- 现让其连续射击,直到命中两次时停止.
- 记随机变量 分别为其第一次和第二次命中时已经射击的次数.
- 计算 ,判断 是否相互独立.
提示:
- 对 ,
例:随机变量向量的函数
- 设 相互独立.
- 定义
- 求 的分布律.
提示:
