第十一讲 指数分布与 Gamma 分布

概率论与数理统计 讲义 NUDT 2023SP

---

---

11.1 指数分布

若连续型 rv $X$ 的 pdf 为

$$f(x;\lambda)=\left\{\begin{array}{cl}\lambda \mathrm{e}^{-\lambda x}& x\geq 0\\ 0 & \text{其他}\end{array}\right.=\lambda \mathrm{e}^{-\lambda x}I_{[0,\infty)}(x)$$

则称其服从参数为 $\lambda(\lambda>0)$ 的指数分布 (exponential distribution)

• 其中 $I_{[0,\infty)}(x)=\left\{\begin{array}{cl}1 & x\geq 0\\ 0 & \text{其他}\end{array}\right.$
• 记为: $X\sim\mathrm{Exp}(\lambda)$
• 如果令 $\beta=1/{\lambda}$, 则记为：$X\sim\mathrm{EXP}(\beta)$

---

指数分布的 pdf 和 cdf

$$f(x;\lambda)=\left\{\begin{array}{cl}\lambda \mathrm{e}^{-\lambda x}& x\geq 0\\ 0 & \text{其他}\end{array}\right.$$

$$F(x;\lambda)=\left\{\begin{array}{cl}0 & x<0\\ 1-\mathrm{e}^{-\lambda x}& x\geq 0\end{array}\right.$$

---

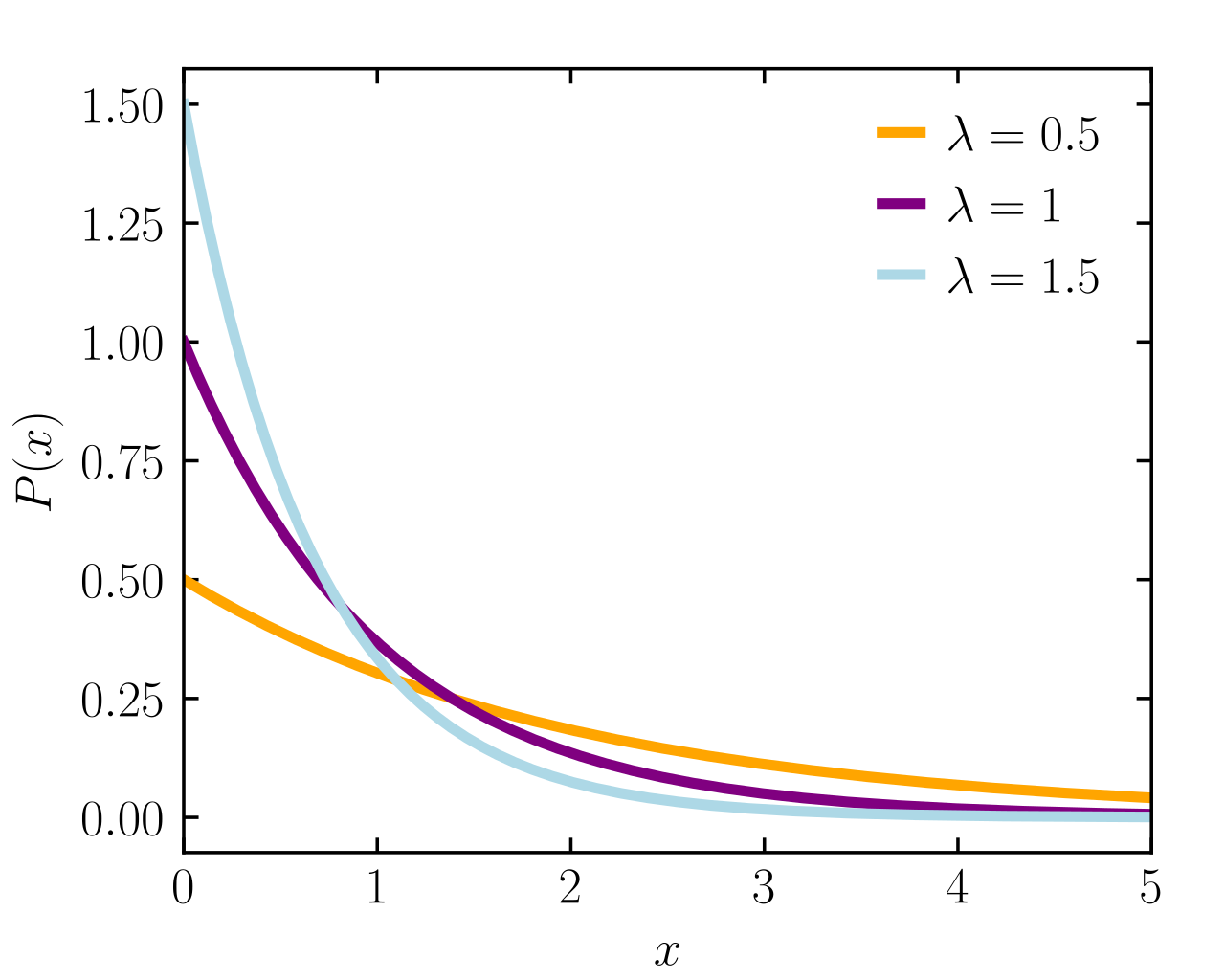
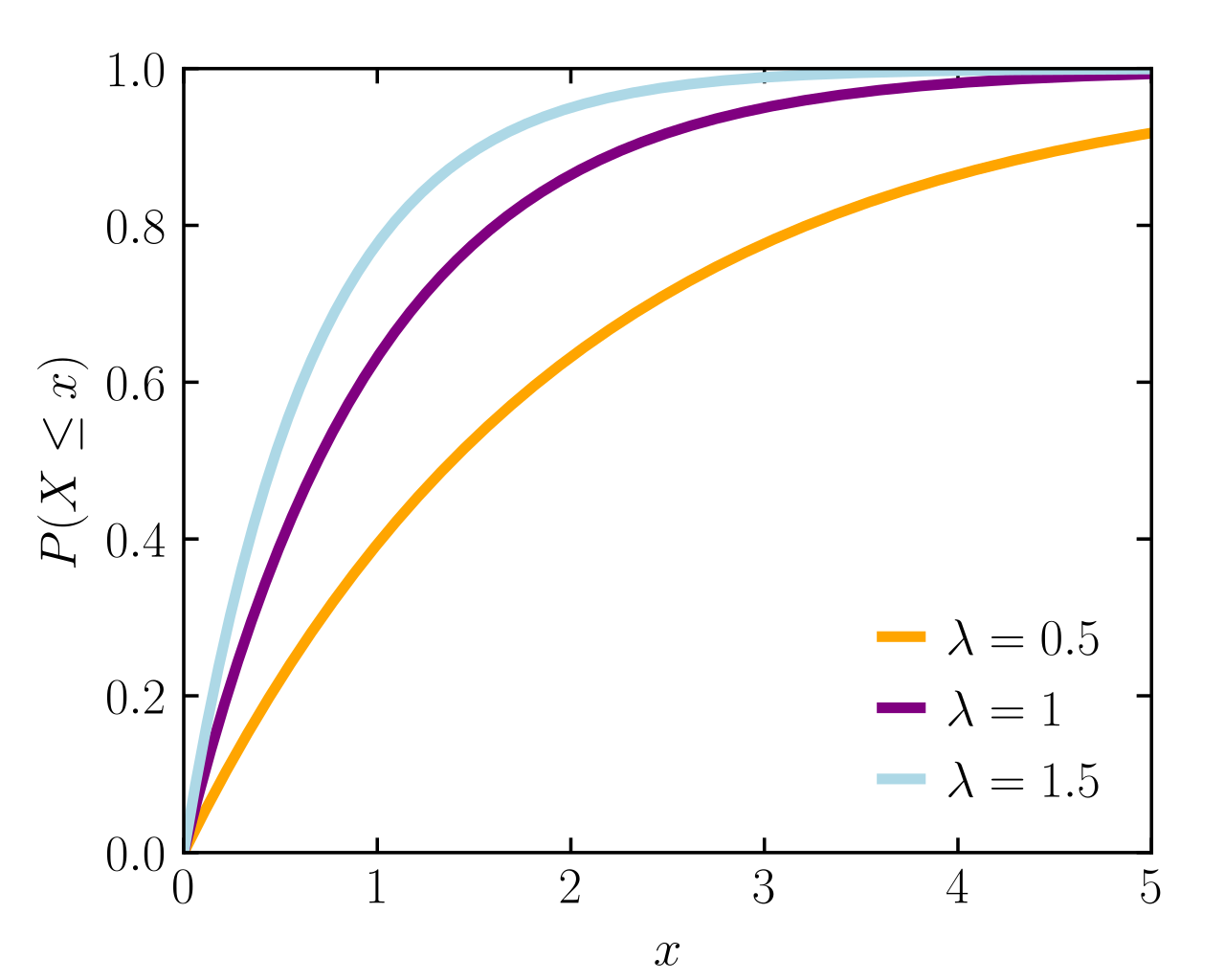
指数分布的期望与方差

定理 若 rv $X\sim\mathrm{Exp}(\lambda)$, 则

• $E(X^n)=\frac{n!}{\lambda^n},\quad n=1,2,...$
• $E(X)=\frac{1}{\lambda}$
• $D(X)=\frac{1}{\lambda^2}$

---

指数分布与 Poisson 分布

对于参数为 $\alpha$ 的 Poisson 过程，在任意给定的时间间隔 $t$ 内，事件出现的次数服从参数为 $\alpha t$ 的 Poisson 分布

• 定理：对于参数为 $\alpha$ 的 Poisson 过程，两个相邻事件发生的时间间隔服从参数为 $\alpha$ 的指数分布

---

证： Poisson 过程具有无记忆性，故不妨定义 rv $X$ 为区间 $(0,t]$ 内事件发生的次数，则 $X\sim P(\alpha t)$.

$$P\{X=k\}=\frac{(\alpha t)^{k}}{k !} \mathrm{e}^{-\alpha t},(k=0,1,2, \cdots).$$

定义 rv $Y$ 为第一次发生对应的时刻，则

$$P\{Y>t\}=P\{X=0\}=\mathrm{e}^{-\alpha t}.$$

由此可得 $Y$ 的 cdf 为 $F_Y(t)=1-\mathrm{e}^{-\alpha t}$, 进而可知 $Y\sim\mathrm{Exp}(\alpha)$.

---

指数分布的无记忆性

定理: 设随机变量 $X\sim\mathrm{Exp}(\alpha)$, 则对任意 $x,y\in\mathbb{R}^+$，

$$P\{X> x+y|X> x\}=P\{X> y\}$$

• 或 ${P\{X>x+y\}=P\{X>x\}P\{X>y\}.}$
• 如果等待时间服从指数分布，那么在已经等待了一段时间的条件下，需要继续等待的时间与前面已经等待的时间没有统计关联.
• 在 Poisson 流中，事件出现的时间间隔与起始时刻无关.

---

证：

• $P\{X>x+y | X>x\}$
  
  • $\displaystyle =\frac{P\{X>x+y, X>x\}}{P\{X>x\}}$
  • $\displaystyle =\frac{P\{X>x+y\}}{P\{X>x\}}=\frac{\int_{x+y}^{\infty} \lambda \mathrm{e}^{-\lambda t} \mathrm{d} t}{\int_{x}^{\infty} \lambda \mathrm{e}^{-\lambda t} \mathrm{d} t}$
  • $\displaystyle =\frac{\mathrm{e}^{-\lambda(x+y)}}{\mathrm{e}^{-\lambda x}}=\mathrm{e}^{-\lambda y}$
  • $\displaystyle =\int_{y}^{\infty} \lambda \mathrm{e}^{-\lambda t} \mathrm{d} t=P\{X>y\}$

---

具有无记忆性的连续型随机变量必服从指数分布

• 设连续型 rv $X$ 满足：$\forall x,y\in\mathbb{R}^+$，$P\{X>x+y\}=P\{X>x\}P\{X>y\}.$
• 记 $G(x)=P\{X>x\}=1-F_X(x)$，则 $G(x)$ 满足 Cauchy 方程:
  
  • $G(x+y)=G(x)G(y)$.
• Cauchy 方程的连续解形如：$G(x)=\exp(\alpha x)$.
• 考虑到 $G(x)\leq 1$，故 $\alpha<0$.
• 记 $\lambda=-\alpha$，则 $F_X(x)=1-G(x)=1-\exp(-\lambda x)$，即 $X\sim\mathrm{Exp}(\lambda)$.

---

指数分布的应用

指数分布常常用来刻画“寿命”的分布.

• 例： 记电子元器件的使用寿命为随机变量 $X$
  
  • 一般认为，$X$ 的主要决定因素是随机出现的电流冲击（shocks），而不是使用过程中的自然损耗（loses）.
  • 电流冲击的出现可以视为一个 Poisson 过程，因此 $X$ 服从指数分布.
  • 记 $X\sim\mathrm{Exp}(\lambda)$，则 $\lambda$ 的含义为 失效率(hazard rate).
  • 记 $\displaystyle X\sim\mathrm{EXP}(\beta),\left(\beta=\frac{1}{\lambda}\right)$，则 $\beta 的含义为 平均寿命(average life).

---

“寿命”的分布

• 电子元器件的使用寿命
• 连续两次网站访问的间隔时间
• 设备故障的间隔时间
• 两次宇宙射线到达的时间间隔
• ... ...

---

失效率

设某个研究对象的寿命为随机变量 $T$，定义其在 $t$ 时刻的失效率（hazard rate）可定义为

$$H(t)=\lim\limits_{\Delta t\to 0}\frac{P\{t<T\leq t+\Delta t|T>t\}}{\Delta t}=\frac{f_T(t)}{1-F_T(t)}.$$

• 通常情况下，$H(t)$ 关于 $t$ 是单调不减的.
• 若 $T\sim\mathrm{Exp}(\lambda)$，则 $H(t)=\lambda$，与时间无关.
• 失效率为常数是指数分布的本征性质.

---

失效率为常数的随机分布

• 设随机变量 $T$ 的失效率为常数 $\lambda$，即：$H(t)=\displaystyle \frac{f_T(t)}{1-F_T(t)}=\lambda.$
• 整理可得：$\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}F_T(t)=\lambda(1-F_T(t))$.
• 给定初值条件：$F_T(0)=0$.
• 求解初值问题可得 $F_T(t)=[1-\exp(-\lambda t)]I_{[0,\infty)}(x)$.
• 结论：失效率为常数的随机变量必服从指数分布.

---

11.2 Gamma 分布

若连续型 rv $X$ 的 pdf 形如

$$f(x;\alpha,\beta)=\left\{\begin{array}{cl}\frac{1}{\beta^{\alpha}\Gamma(\alpha)}x^{\alpha-1}\mathrm{e}^{-x/\beta}& x\geq 0\\ 0 & \text{其他}\end{array}\right.$$

其中 $\alpha,\beta>0$，则称 $X$ 服从参数为 $\alpha,\beta$ 的 Gamma 分布.

• 记为：$X\sim\Gamma(\alpha,\beta)$

---

Gamma 函数

对 $\alpha>0$, Gamma 函数 $\Gamma(\alpha)$ 定义为

$$\Gamma(\alpha)=\int_{0}^{\infty}x^{\alpha-1}\mathrm{e}^{-x}\mathrm{d}x$$

• 对任意 $\alpha>1$, $\Gamma(\alpha)=(\alpha-1)\cdot\Gamma(\alpha-1)$
  
  • 特别地，对任意正整数 $n$, $\Gamma(n)=(n-1)!$
• $\Gamma\left(\frac12\right)=\sqrt{\pi}$

---

复平面上的 Gamma 函数

---

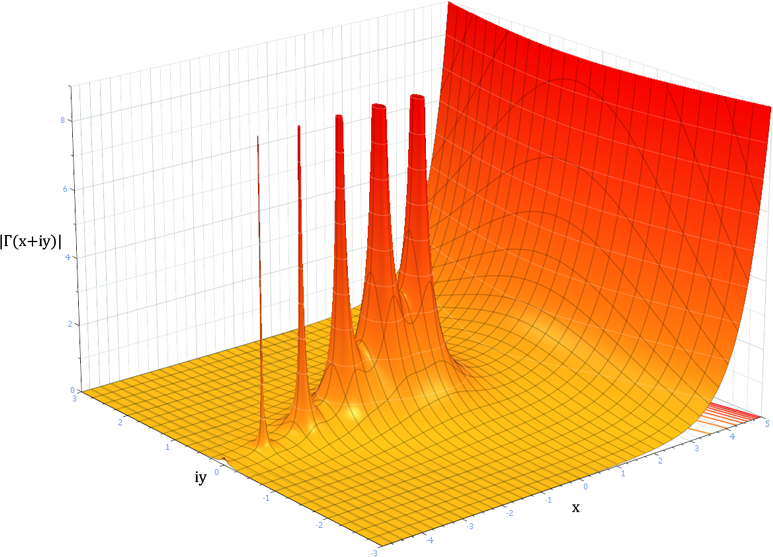
Gamma 分布的特殊情形

• 如果 $\beta=1$, 可以得到 标准 Gamma 分布，pdf 为
  
  • $f(x;\alpha)=\left\{\begin{array}{cl}\frac{x^{\alpha-1}\mathrm{e}^{-x}}{\Gamma(\alpha)}& x\geq 0\\ 0 & \text{其他}\end{array}\right.$
• 若 $\alpha=1$, 则 $X\sim\mathrm{EXP}(\beta)$, pdf 为
  
  • $f(x;\beta)=\left\{\begin{array}{cl}\frac{1}{\beta}\mathrm{e}^{-x/\beta}& x\geq 0\\ 0 & \text{其他}\end{array}\right.$

---

Gamma 分布的密度曲线

---

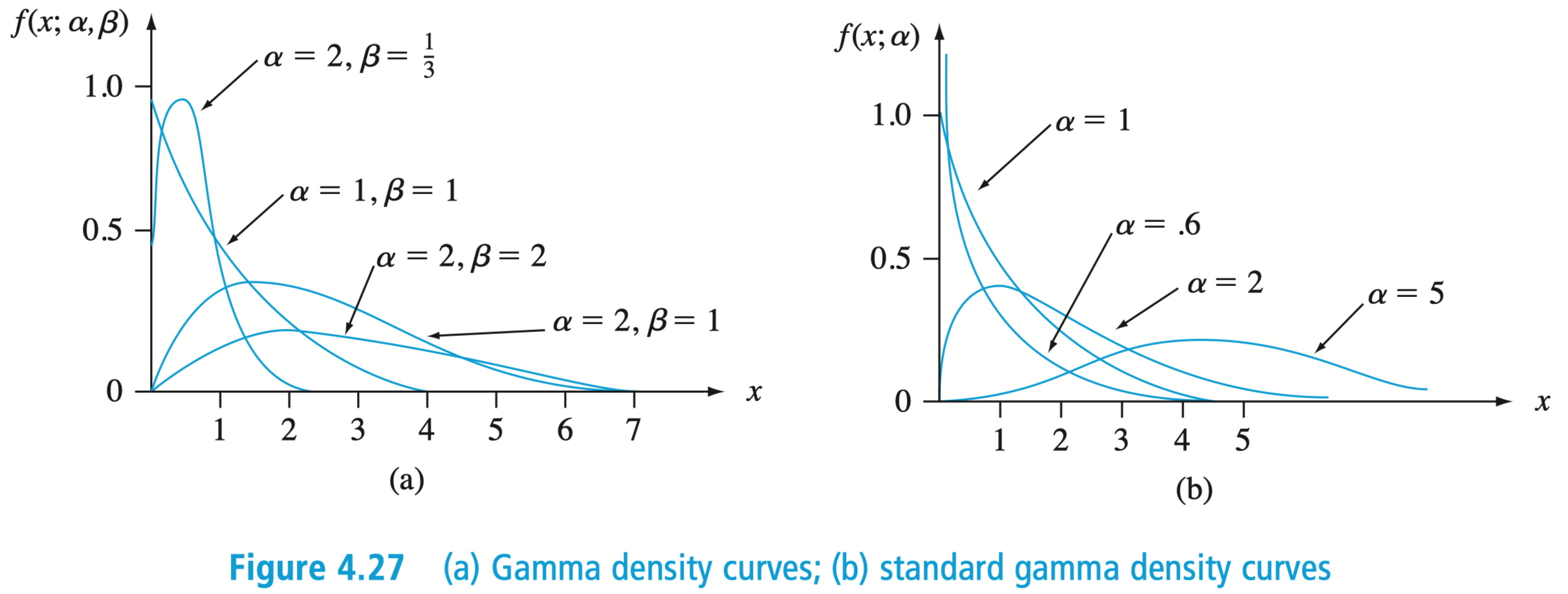
Gamma 分布的期望与方差

定理： 设 rv $X\sim\Gamma(\alpha,\beta)$，则

• $E(X)=\alpha\beta$
• $D(X)=\alpha\beta^2$

---

证：

• $E(X)=\int_{-\infty}^{\infty}x\cdot\frac{1}{\beta^{\alpha}\Gamma(\alpha)}x^{\alpha-1}\mathrm{e}^{-x/\beta}\mathrm{d}x$
  
  • $=\frac{\beta}{\Gamma(\alpha)}\int_{-\infty}^{\infty}\left(\frac{x}{\beta}\right)^{\alpha}\mathrm{e}^{-x/\beta}\mathrm{d}\frac{x}{\beta}$
  • $=\frac{\beta}{\Gamma(\alpha)}\int_{-\infty}^{\infty}y^{\alpha}\mathrm{e}^{-y}\mathrm{d}y\quad\quad \left(\text{记 }y=\frac{x}{\beta}\right)$
  • $=\frac{\beta}{\Gamma(\alpha)}\Gamma(\alpha+1)=\alpha\beta$

---

• $E(X^2)=\int_{-\infty}^{\infty}x^2\cdot\frac{1}{\beta^{\alpha}\Gamma(\alpha)}x^{\alpha-1}\mathrm{e}^{-x/\beta}\mathrm{d}x$
  
  • $=\frac{\beta^2}{\Gamma(\alpha)}\int_{-\infty}^{\infty}\left(\frac{x}{\beta}\right)^{\alpha+1}\mathrm{e}^{-x/\beta}\mathrm{d}\frac{x}{\beta}$
  • $=\frac{\beta^2}{\Gamma(\alpha)}\int_{-\infty}^{\infty}y^{\alpha+1}\mathrm{e}^{-y}\mathrm{d}y\quad\quad \left(\text{记 }y=\frac{x}{\beta}\right)$
  • $=\frac{\beta^2}{\Gamma(\alpha)}\Gamma(\alpha+2)=\beta^2(\alpha+1)\alpha$
• $D(X)=E(X^2)-\left[E(X)\right]^2=\alpha\beta^2$

---

Gamma 分布的应用

• Gamma 分布也是一种“寿命”的分布
• 例：具有冷备份的冗余系统，记其寿命为随机变量 $X$
  
  • 系统中共有 $\alpha$ 个部件，每个的平均寿命是 $\beta$.
  • 系统运行时，只有一个部件处于工作状态.
  • 如果运行中的部件失效，则启动一个后备的部件.
  • 记每个部件的寿命为 $X_i,i=1,...,\alpha$，$X_i\sim\mathrm{EXP}(\beta)$.
  • 若每个部件的寿命相互独立，则 $X= \sum\limits_{i=1}^{\alpha}X_i \sim\Gamma(\alpha,\beta)$.

---

小结

• 指数分布：$X\sim\mathrm{Exp}(\lambda)$
  
  • 熟练掌握：cdf、pdf、期望、方差
• 指数分布的性质
  
  • 与 Poisson 分布的关系
  • 无记忆性
• 了解 Gamma 分布和指数分布族

---

Logic and mathematics are nothing but specialised linguistic structures.
-- Jean Piaget

---

指数分布族

形如

$$f_X(x;\boldsymbol{\theta})=h(x)\exp(\boldsymbol{\lambda}^{\mathrm{T}}(\boldsymbol{\theta})\boldsymbol{\phi}(x)-A(\boldsymbol{\theta})),\;(x\in\mathbb{R}).$$

的一元 pdf/pmf 统称 指数族概率函数 (exponential family).

其中 $\boldsymbol{\theta}\in\mathbb{R}^n$，$\boldsymbol{\lambda}:\mathbb{R}^n\to\mathbb{R}^n$，$\boldsymbol{\phi}:\mathbb{R}\to\mathbb{R}^n$, $h:\mathbb{R}\to \mathbb{R}$,

$$A(\boldsymbol{\theta})=\ln\int_{\mathbb{R}}h(x)\exp(\boldsymbol{\lambda}^{\mathrm{T}}(\boldsymbol{\theta})\boldsymbol{\phi}(x))\mathrm{d}x.$$

---

正态分布

$$f_X(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right).$$

• $\boldsymbol{\theta}=(\mu,\sigma)^{\mathrm{T}}$
• $\boldsymbol{\lambda}(\boldsymbol{\theta})=\left(\frac{\mu}{\sigma^2},-\frac{1}{2\sigma^2}\right)^{\mathrm{T}}$
• $\displaystyle\boldsymbol{\phi}(x)=(x,x^2)^{\mathrm{T}}$
• $h(x)=\frac{1}{\sqrt{2\pi}}$
• $A(\boldsymbol{\theta})=\frac{\mu^2}{2\sigma^2}+\ln\sigma$

---

指数分布

$$\begin{aligned} f_X(x)&=\mu\exp(-\mu x)I_{[0,\infty)}(x)\\ &=\left\{\begin{array}{cl} \mu\exp(-\mu x), & x\geq 0 \\ 0, & x<0 \end{array}\right. \end{aligned}$$

• ${\theta}=\mu$
• ${\lambda}({\theta})=-\theta$
• $h(x)=\mu I_{[0,\infty)}(x)$
• $A({\theta})=0$

---

二项分布

$$\begin{aligned} P\{X=x\}&=C_n^xp^x(1-p)^{n-x}\\ &=C_n^x\exp\left[x\ln\frac{p}{1-p}+n\ln(1-p)\right] \end{aligned}$$

• ${\theta}=p$
• ${\lambda}({\theta})=\ln\frac{\theta}{1-\theta}$
• $h(x)=C_n^x$
• $A({\theta})=-n\ln(1-\theta)$

---

Poisson 分布

$$P\{X=x\}=\frac{\mu^x}{x!}\exp(-\mu)=\frac{1}{x!}\exp(x\ln\mu-\mu)$$

• ${\theta}=\mu$
• ${\lambda}({\theta})=\ln\theta$
• $h(x)=\frac{1}{x!}$
• $A({\theta})=\theta$

---

带有线性约束的最大熵问题

• $\displaystyle \max\limits_f\left(-\int_{\mathbb{R}}f(x)\ln(f(x))\mathrm{d}x\right)$
  
  • $\displaystyle \mathrm{s.t.} \int_{\mathbb{R}}f(x)\mathrm{d}x=1$ and $\displaystyle \int_{\mathbb{R}}\phi_k(x)f(x)\mathrm{d}x=m_k,\;k=1,...,n.$
• 解之可得：$\displaystyle f(x)\varpropto\exp\left( \sum\limits_{k=1}^n\theta_k\phi_k(x) \right)$
• 结论：在线性约束下，最大熵分布都属于指数分布族.