@blueband21c
2023-04-24T12:43:26.000000Z
字数 7041
阅读 2715
第十八讲 条件数学期望
概率论与数理统计 讲义 NUDT 2023SP
随机变量的条件分布
- 离散型:条件分布律
- 取值范围:,前提:
- 连续型:条件密度
- 取值范围:,前提:
18.1 条件数学期望
离散型: 若 ,则称
为 对 在 条件下的条件数学期望连续型: 若 ,则称
为 对 在 条件下的条件数学期望
条件期望的几何意义
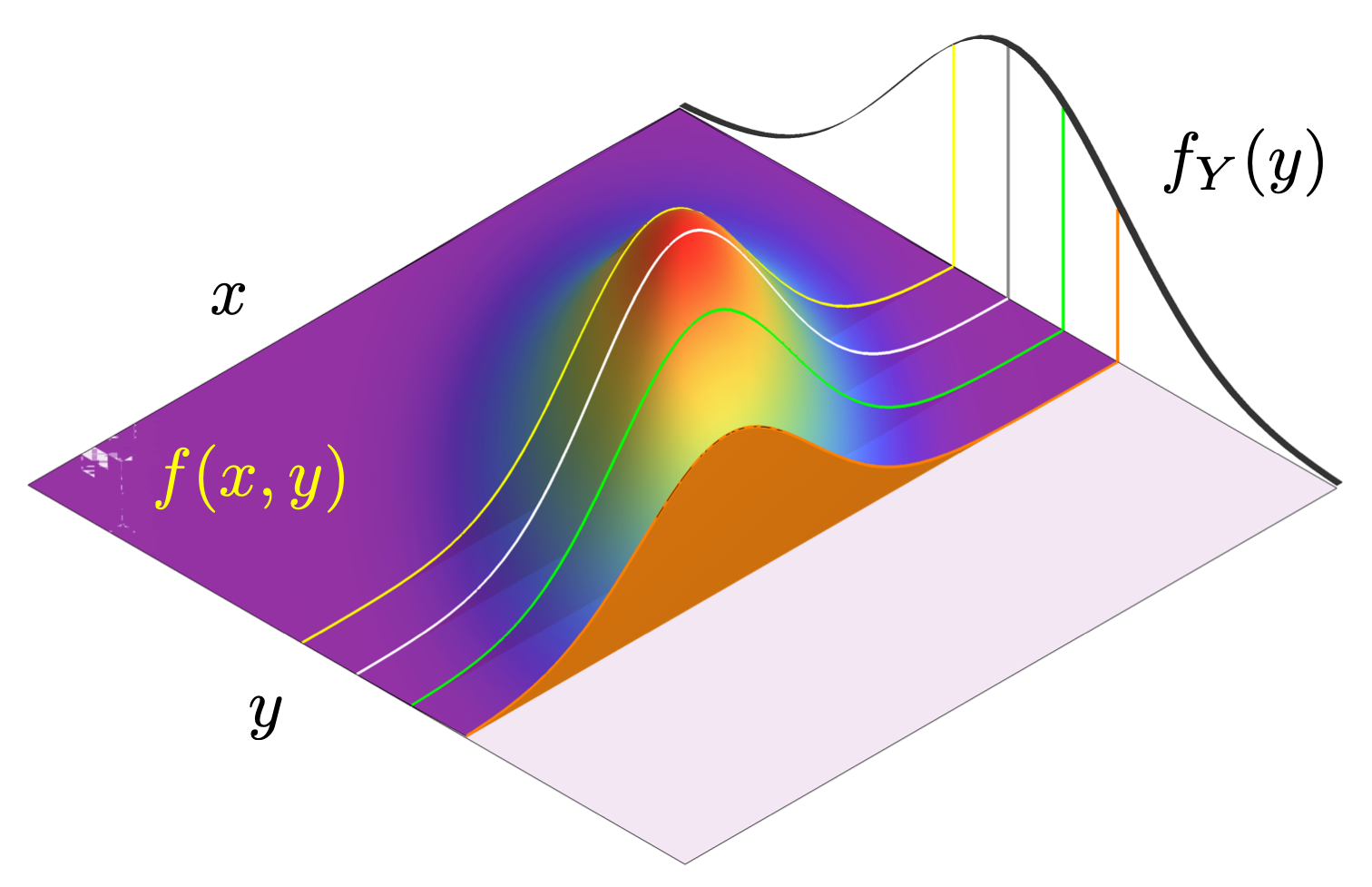
例 设 服从平面区域 上的均匀分布,求 .
提示:
- .
条件期望的本质
- 是一个数.
- 的值与 有关.
- 是随机变量 的取值.
- 故 是某个
随机变量的值. - 将这个随机变量记为 ,称为 对 的条件期望.
例 设 服从单位圆上的均匀分布,求 和 .
18.2 全期望公式
- 根据随机变量 的类型
- 离散型:
- 连续型:
例: 设随机变量 有密度函数
随机变量 ,求 及 .
提示:
- 时,,故 .
-
全期望公式与全概率公式
- 设 是一个事件,其
示性函数 - 进而 ,.
- 令 ,代入全期望公式即得全概率公式
连续型的全概率公式
例 如图,在 内任取一点 ,在其底边 上任取一点 ,求直线 与 相交的概率.
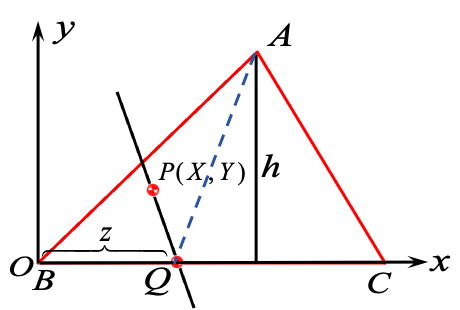
- 提示: 定义 rv
- 事件 :直线 与 相交
- 发生,当且仅当
- 由全概率公式
条件期望的性质
- 若 相互独立,则
- 对常数 ,
- 对任意 ,
- 设 为连续函数,则
例:顾客的平均消费额
- 设进入某商店的顾客购买商品的概率是 .
- 购买商品的顾客的消费金额 .
- 求每个顾客的平均消费金额.
提示:
- 定义事件 :顾客购买商品
- rv 表示顾客消费的金额,则
- 由全期望公式
-
例:巴格达窃贼问题
- 某窃贼被关在3个门的地牢中.
- 1号门通向自由,出这个门3小时后便回到地面;
- 2号门通向一个通道,在此通道中走5个小时返回地牢;
- 3号门通向一个更长的通道,在此通道中走7个小时返回地牢;
- 如果窃贼选择3个门的可能性相等,求他为获得自由奔走的平均时长.
提示:
- 设窃贼需要走 小时到达地面, 为其每次选择的门的编号.
- .
- 由已知 ,,.
- 代入计算 .
- 解得 .
随机个随机变量之和的期望
定理 假设 为独立同分布的随机变量序列,其期望与方差均存在,分别记为 . 如果 为取值自然数的随机变量,与每个 独立,且 都存在,则
- .
- .
证明:1. .
证明:2.
- 因为 相互独立,故
-
-
例:商店的平均营业额
- 某商店一天内到达的顾客数 ,顾客购买商品的概率是 ,而购买商品的顾客消费金额 .
- 假设每个顾客是否购买商品是独立的,且 与 独立.
- 求商店一天的平均营业额.
提示:
- 设每个顾客消费的金额为
- 由前例
18.3 最优预测的构造
定理 设 的二阶矩均存在,若以连续函数 作为 的预测,则当 时均方误差 取最小值.
- 即:对任意 ,总有 .
- 称 为 关于 的回归函数.
提示: 以连续型为例. 记 的联合密度与边缘密度分别为 .
-
- 其中 是在 条件下 的条件分布关于直线 的转动惯量.
- 由方差的性质,当且仅当 时该值取到最小,为 .
- 因为 非负,由此即知 使得 达到最小.
二维正态分布
设 ,求 关于 的回归函数.
- 可见 关于 的条件分布仍然是正态分布,于是易知所求回归函数
小结
- 条件期望 是随机变量
全期望公式
- 全概率公式
随机个随机变量之和的期望
