第十讲 正态分布

概率论与数理统计 讲义 NUDT 2023SP

---

---

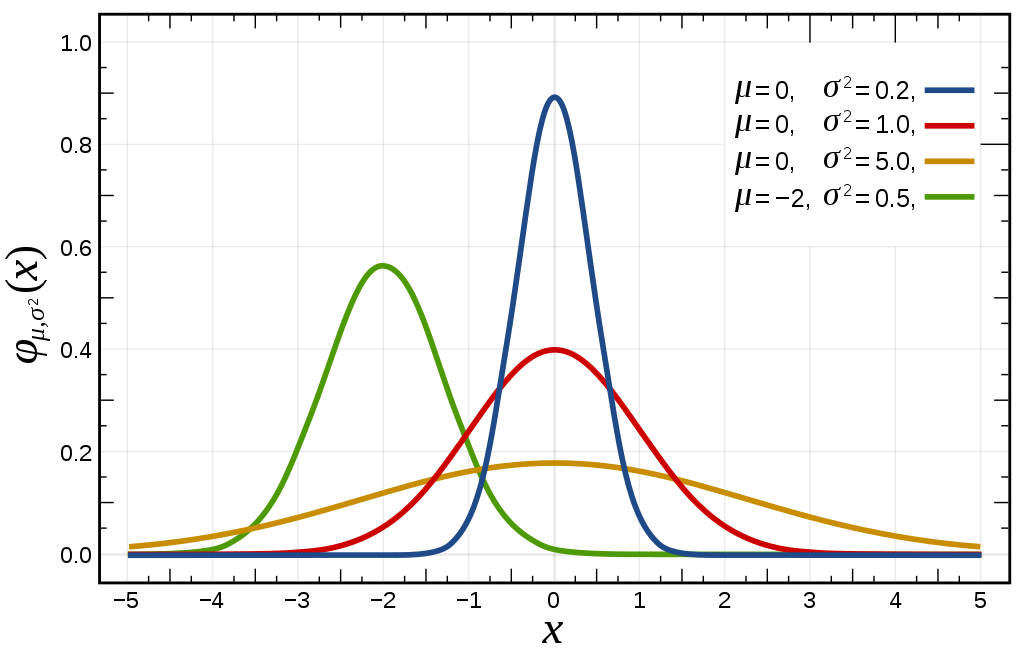
10.1 正态分布

如果连续型 rv $X$ 的 pdf 为

$$f(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}\mathrm{e}^{-\frac{(x-\mu)^2}{2\sigma^2}},\quad (-\infty<x<\infty)$$

则称 $X$ 服从参数为 $\mu$ 和 $\sigma>0$ 的正态分布 (Normal distribution)

• 记为: $X\sim N(\mu,\sigma^2)$

---

Gauss 积分

$$\int_{-\infty}^{\infty}\mathrm{e}^{-x^2}\mathrm{d}x=\sqrt{\pi}$$

• 记 $u=\frac{x-\mu}{\sqrt{2}\sigma}$
• $\int_{-\infty}^{\infty}f(x;\mu,\sigma)\mathrm{d}x=\int_{-\infty}^{\infty}\frac{1}{\sigma\sqrt{2\pi}}\mathrm{e}^{-\frac{(x-\mu)^2}{2\sigma^2}}\mathrm{d}x$
  
  • $=\frac{1}{\sqrt{\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-u^2}\mathrm{d}u=1$
• 正态分布也称为 Gauss 分布（Gaussian distribution）或 Laplace-Gauss 分布

---

正态分布的期望与方差

定理 设 rv $X\sim N(\mu,\sigma^2)$, 则

• $E(X)=\mu$
• $D(X)=\sigma^2$

---

证： 记 $f(x)=f(x;\mu,\sigma)$.

• $E(X)=\int_{-\infty}^{\infty}xf(x)\mathrm{d}x$
  
  • $=\int_{-\infty}^{\infty}(x-\mu)f(x)\mathrm{d}x+\mu\int_{-\infty}^{\infty}f(x)\mathrm{d}x$
  • $=\int_{-\infty}^{\infty}(x-\mu)\frac{1}{\sigma\sqrt{2\pi}}\mathrm{e}^{-\frac{(x-\mu)^2}{2\sigma^2}}\mathrm{d}x+\mu$
  • $=\int_{-\infty}^{\infty}y\frac{1}{\sigma\sqrt{2\pi}}\mathrm{e}^{-\frac{y^2}{2\sigma^2}}\mathrm{d}y+\mu \quad\left( y=x-\mu\right)$
  • $=0+\mu=\mu$

---

• $D(X)=E[(X-E(X))^2]=E[(X-\mu)^2]$
  
  • $=\int_{-\infty}^{\infty}(x-\mu)^2\frac{1}{\sqrt{2\pi}\sigma}\mathrm{e}^{-\frac{(x-\mu)^2}{2\sigma^2}}\mathrm{d}x$
  • $=\frac{2\sigma^2}{\sqrt{\pi}}\int_{-\infty}^{\infty}y^2\mathrm{e}^{-y^2}\mathrm{d}y \quad \left(\text{记 } y=\frac{x-\mu}{\sqrt2\sigma}\right)$
  • $=\frac{\sigma^2}{\sqrt{\pi}}\int_{-\infty}^{\infty}y\mathrm{e}^{-y^2}\mathrm{d}y^2$
  • $=\frac{\sigma^2}{\sqrt{\pi}}\left(-y\mathrm{e}^{-y^2}\bigg|_{-\infty}^{\infty}+\int_{-\infty}^{\infty}\mathrm{e}^{-y^2}\mathrm{d}y\right)$
  • $=\frac{\sigma^2}{\sqrt{\pi}}\left(-0+0+\sqrt{\pi}\right)=\sigma^2$

---

$$\begin{aligned} E\left[(X-\mu)^n\right]&=\displaystyle\int_{-\infty}^{\infty}(x-\mu)^n\dfrac{1}{\sigma\sqrt{2\pi}}\exp\left[-\dfrac{(x-\mu)^2}{2\sigma^2}\right]\mathrm{d}x\quad\left(\text{令 } y=\dfrac{x-\mu}{\sigma\sqrt{2}}\right)\\ &=\dfrac{2^{n/2}\sigma^n}{\sqrt{\pi}}\displaystyle\int_{-\infty}^{\infty}y^n\exp(-y^2)\mathrm{d}y \end{aligned}$$

当 $n$ 为奇数时，被积函数是奇函数，上式等于 $0$; 若 $n$ 为偶数，则令 $z=y^2$，于是

$$\begin{aligned} E\left[(X-\mu)^n\right]&=\dfrac{2^{n/2}\sigma^n}{\sqrt{\pi}}\displaystyle\int_{0}^{\infty}z^{\frac{n-1}{2}}\mathrm{e}^{-z}\mathrm{d}z=\dfrac{2^{n/2}\sigma^n}{\sqrt{\pi}}\Gamma\left(\dfrac{n+1}{2}\right)\\ &=\dfrac{2^{n/2}\sigma^n}{\sqrt{\pi}}\dfrac{n-1}{2}\dfrac{n-3}{2}\cdots\dfrac{1}{2}\Gamma\left(\dfrac{1}{2}\right)=(n-1)!!\sigma^n \end{aligned}$$

---

10.2 标准正态分布

概率分布 $N(0,1)$ 称为 标准正态分布(standard normal distribution).

• 标准正态 rv 一般记为 $Z$，其 pdf 为

  • $f(z;0,1)=\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{z^2}{2}},\quad (-\infty<z<\infty)$

• $Z\sim N(0,1)$ 的 cdf 一般记为 $\Phi(z)$.

---

标准正态分布的密度与分布函数

---

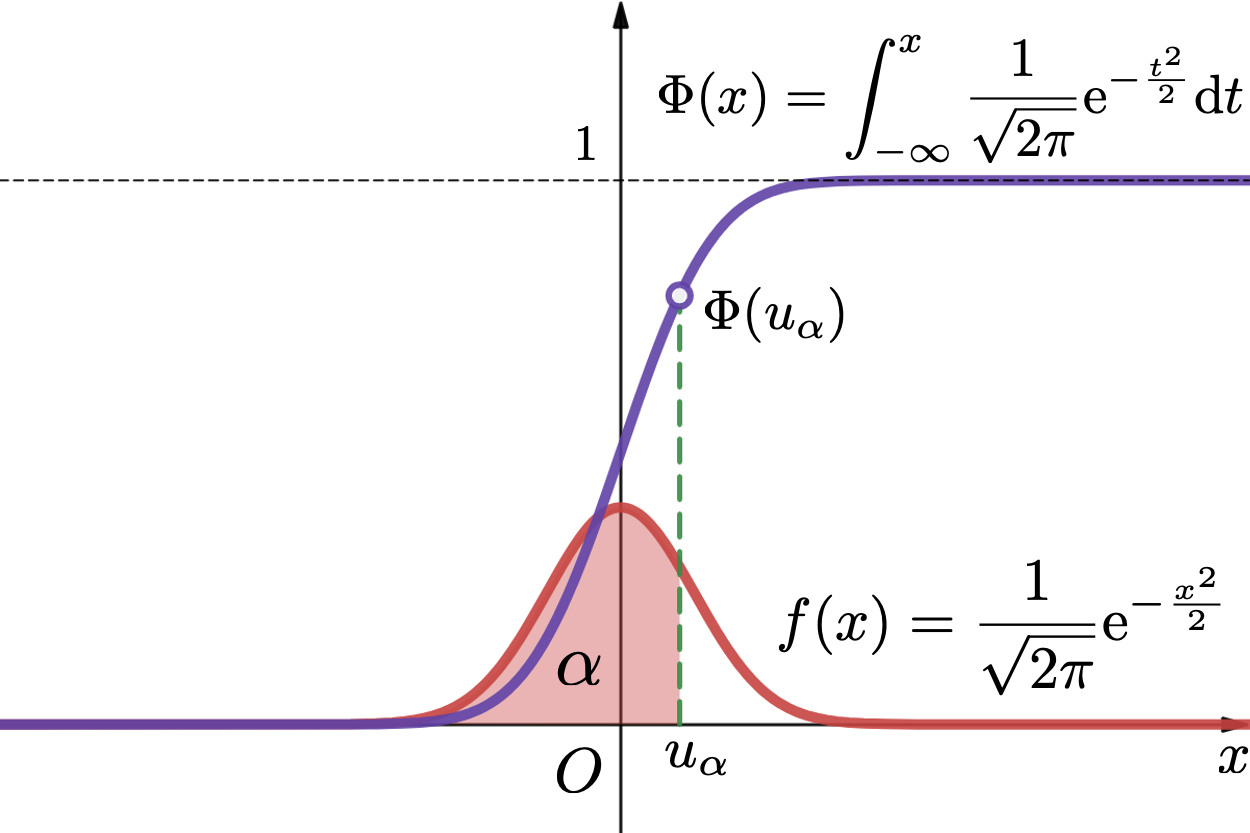
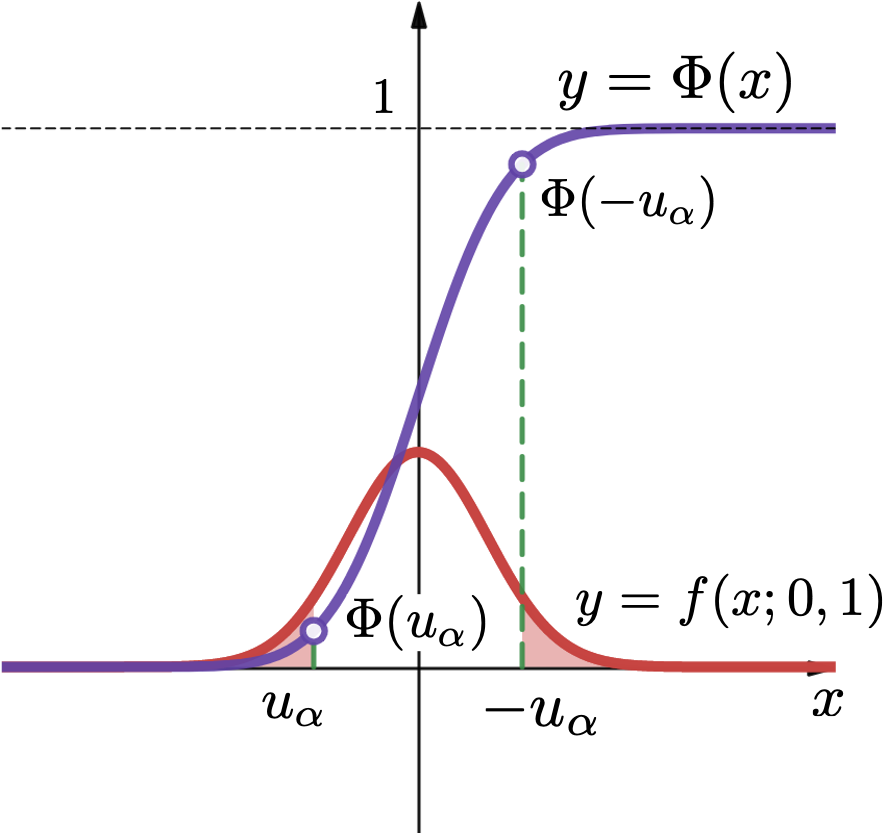
标准正态分布的分位点

给定 $0<\alpha<1$, 标准正态分布的 $\alpha$ 分位点 $u_{\alpha}$ 定义为

$${\Phi(u_{\alpha})=\alpha.}$$

• 对称性：
  
  1. ${-u_{\alpha}=u_{1-\alpha}.}$
  2. ${\Phi(u_{\alpha})+\Phi(-u_{\alpha})=1.}$

---

正态分布 rv 的线性变换

定理 设 rv $X\sim N(\mu,\sigma^2)$, 定义

$$Y=aX+b,\;(a,b\in\mathbb{R})$$

则 $Y\sim N(a\mu+b,a^2\sigma^2)$.

• 正态随机变量经过线性变换仍服从正态分布.
• 推论：$X\sim N(\mu,\sigma^2)$，则 $Z=\frac{X-\mu}{\sigma}\sim N(0,1)$.

---

证明 $\bbox[yellow]{Y=aX+b\sim N(a\mu+b,a^2\sigma^2).}$

设 $a>0$（$a<0$ 的情况可以类似证明）.

$$F_Y(y)=P\{Y\leq y\}=P\{aX+b\leq y\}=P\{X\leq\dfrac{y-b}{a}\}=F_X\left(\dfrac{y-b}{a}\right)$$

$$\begin{aligned} f_Y(y)&= \dfrac{\mathrm{d}}{\mathrm{d}y}F_Y(y)=\dfrac{\mathrm{d}}{\mathrm{d}y}F_X\left(\dfrac{y-b}{a}\right)=f_X\left(\dfrac{y-b}{a}\right)\dfrac{1}{a}\\ &=\dfrac{1}{a\sigma\sqrt{2\pi}}\exp\left[-\dfrac{1}{2\sigma^2}\left(\dfrac{y-b}{a}-\mu\right)^2\right]\\ &=\dfrac{1}{a\sigma\sqrt{2\pi}}\exp\left\{-\dfrac{1}{2(a\sigma)^2}\left[y-(a\mu+b)\right]^2\right\} \end{aligned}$$

由此可知 $Y\sim N(a\mu+b,a^2\sigma^2)$.

---

正态随机变量相关的概率计算

推论 设 rv $X\sim N(\mu,\sigma^2)$, 则

• $P\{X\leq b\}=\Phi\left(\frac{b-\mu}{\sigma}\right)$
• $P\{X\geq a\}=1-\Phi\left(\frac{a-\mu}{\sigma}\right)$
• $P\{a\leq X\leq b\}=\Phi\left(\frac{b-\mu}{\sigma}\right)-\Phi\left(\frac{a-\mu}{\sigma}\right)$

---

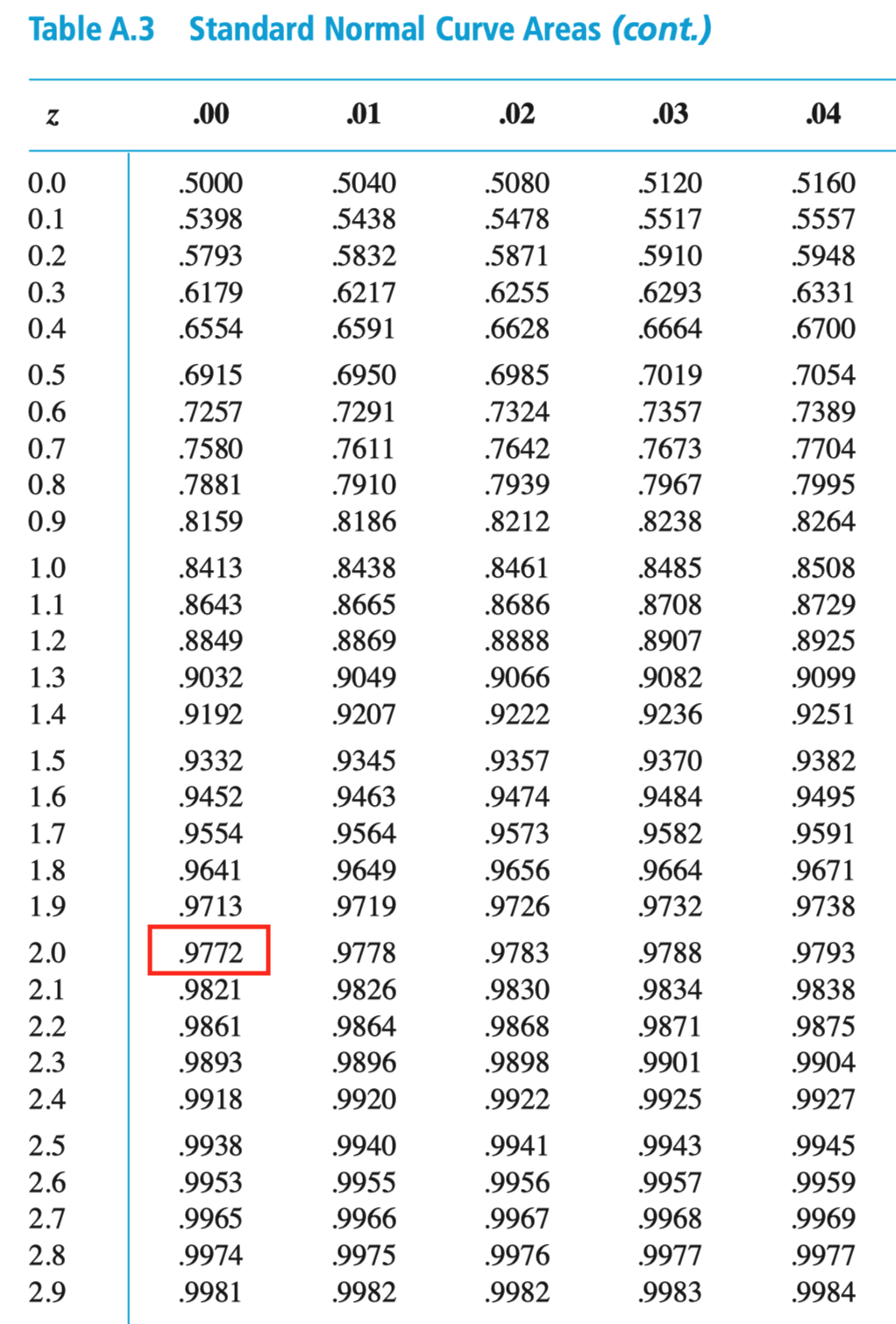
例：男性身高超过 1.9 m 的概率

设成年男性的身高 $X\sim N(1.70,0.1^2)$. 任选一名成年男性，求其身高超过 $1.90$ 米的概率.

---

解： 令 $Z=\frac{X-1.70}{0.1}$, 则 $Z\sim N(0,1)$.

$$\begin{aligned} P&\{X>1.9\}=P\left\{\frac{X-1.7}{0.1}>\frac{1.9-1.7}{0.1}\right\}\\ &=P\{Z>2\}=1-\Phi(2)\approx 1-0.9772=0.0228. \end{aligned}$$

---

例：走哪条路更好？

某人上班通勤有两条不同的路径:

• 路径 I: 穿过城市中心，所需时间 $X\sim N (50,10^2)$ (距离短，车流量大)

• 路径 II: 走环线，所需时间 $X \sim N (60,4^2)$ (距离长，车流量小)

  1. 如果有 $70$ 分钟的时间，走哪条路比较好？
  2. 如果只有 $65$ 分钟的时间，走哪条路比较好？

---

解： 选择道路的依据是走该道路能够按时到达的概率，即：要优先选择 $P\{X\leq \text{给定时限}\}$ 更大的路径.

如果有 $70$ 分钟可用. 对于路径 I: $\frac{X-50}{10}\sim N(0,1)$,

$$P\{X \leq 70\}=\Phi\left(\frac{70-50}{10}\right)=\Phi(2)=0.9772$$

对于路径 II: $\frac{X-60}{4}\sim N(0,1)$,

$$P\{X \leq 70\}=\Phi\left(\frac{70-60}{4}\right)=\Phi(2.5)=0.9938.$$

由此可见，应该选择路径 II.

---

如果有 $65$ 分钟可用. 对于路径 I: $\frac{X-50}{10}\sim N(0,1)$,

$$P\{X \leq 65\}=\Phi\left(\frac{65-50}{10}\right)=\Phi(1.5)=0.9332$$

对于路径 II: $\frac{X-60}{4}\sim N(0,1)$,

$$P\{X \leq 65\}=\Phi\left(\frac{65-60}{4}\right)=\Phi(1.25)=0.8944$$

由此可见，此时应该选择路径 I.

---

正态分布的应用

• 正态分布常常被称为误差的分布，适合于用来刻画各种随机误差相关的指标.
• 如果一个随机指标是由数量众多且相互独立的微小因素叠加而成的，那么这个随机指标将服从或近似地服从正态分布.
• 例如：各种测量的误差、炮弹落点的偏差、某个班级的课程考试成绩、成年人的身高与体重、一个地区的家庭年收入、农作物产量、海浪的高度，等等.
• 中心极限定理为以上的论述提供了理论依据.

---

10.3 正态分布的其他性质

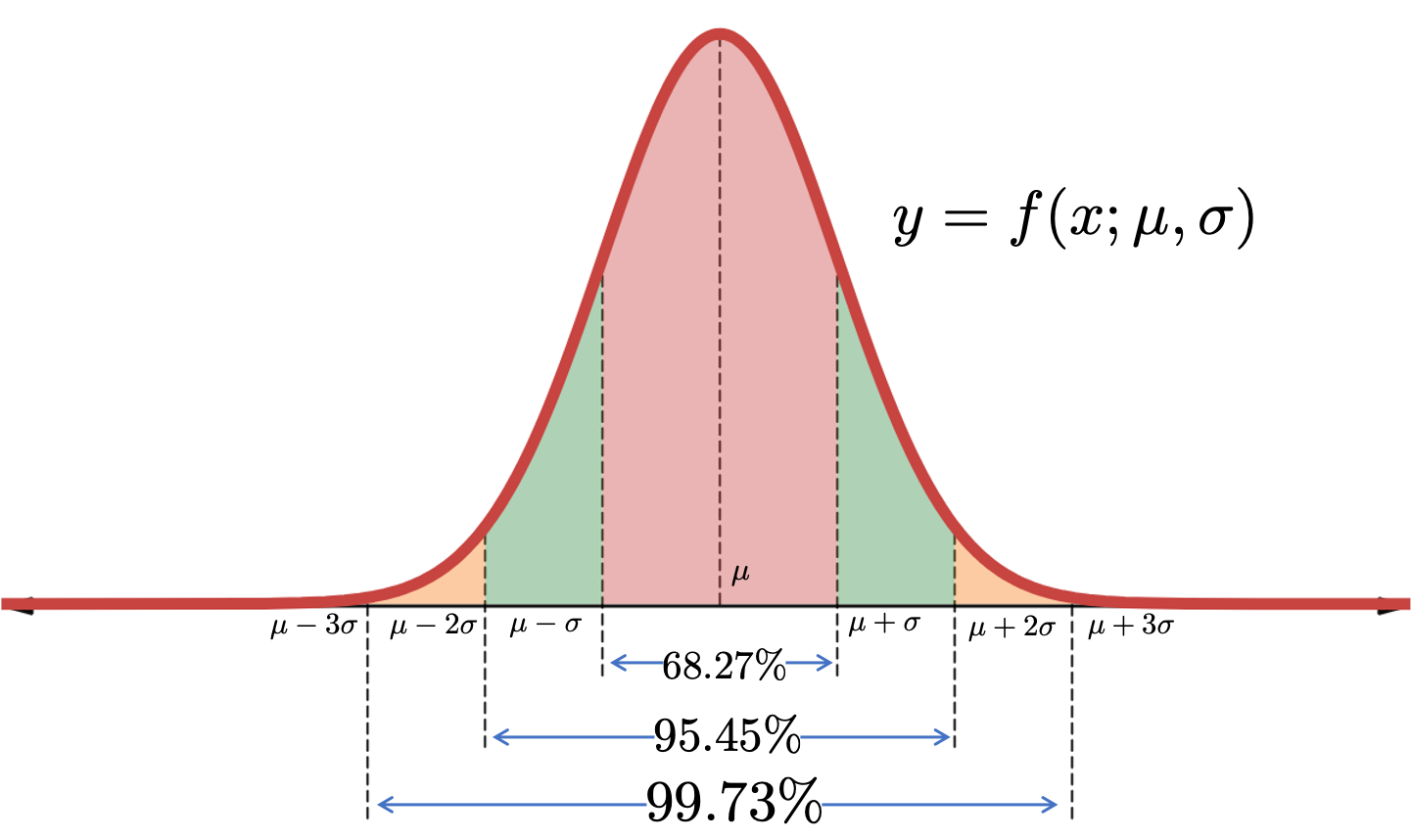
3-σ 原理

---

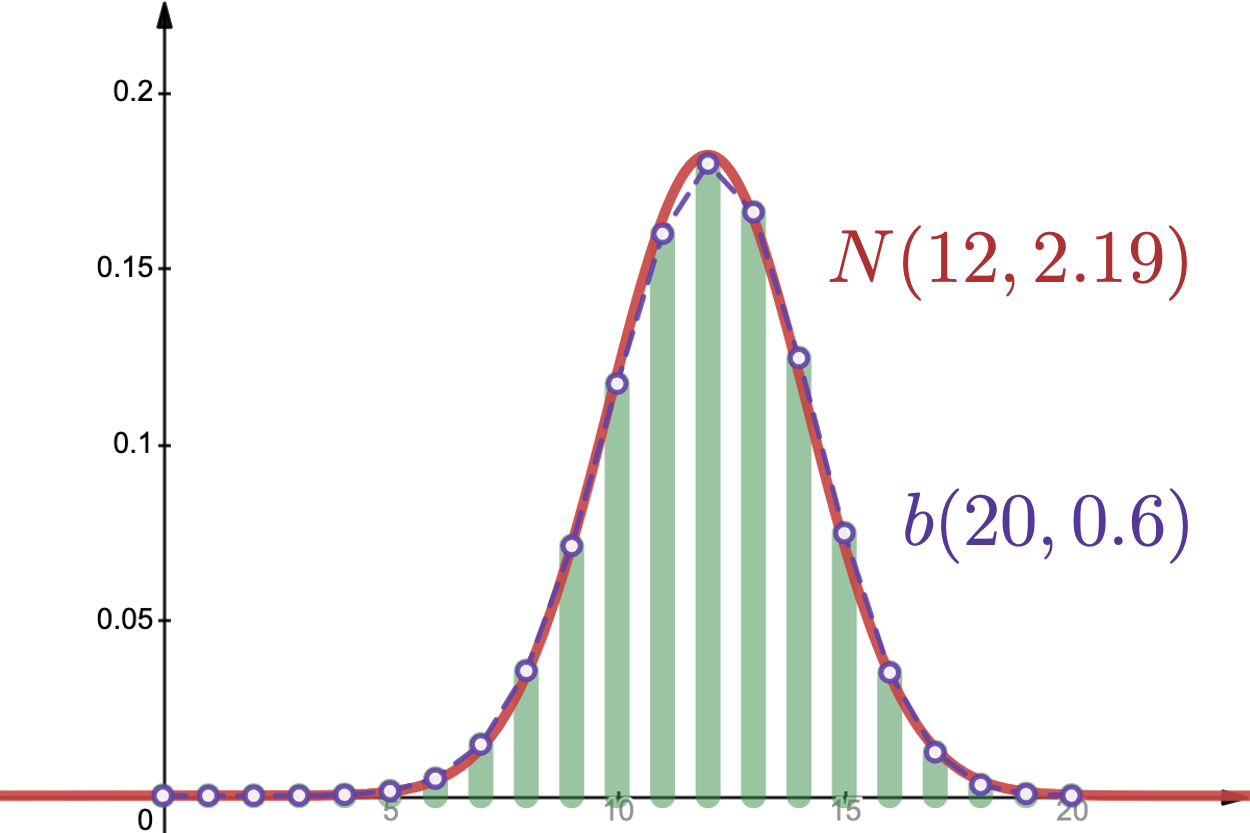
二项分布的正态近似

---

Galton 钉板

• Also known as the Bean Machine or quincunx, is a device invented by Sir Francis Galton to demonstrate the central limit theorem.
• In particular with sufficient sample size the binomial distribution approximates a normal distribution.

Sir Francis Galton (1822-1911)

• English Victorian era statistician, polymath, sociologist, psychologist, anthropologist, eugenicist, tropical explorer, geographer, inventor, meteorologist, proto-geneticist, and psychometrician.
• Created the statistical concept of correlation and widely promoted regression toward the mean.

---

小结

• 正态分布：$N(\mu,\sigma^2)$
  
  • pdf： $f(x)=\frac{1}{\sqrt{2\pi}\sigma}\mathbb{e}^{-\frac{(x-\mu)^2}{2\sigma^2}}$
  • $E(X)=\mu,\;D(X)=\sigma^2$
  • 线性性： $aX+b\sim N(a\mu+b,a^2\sigma^2)$
• 标准正态分布：$N(0,1)$
  
  • cdf：$\Phi(x)$
  • 分位点：$\Phi(u_{\alpha})=\alpha$
• 重点：用 $\Phi(x)$ 表示任意正态随机变量相关的概率

---

It is impossible to be a mathematician without being a poet in soul.
-- Sofia Vasilyevna Kovalevskaya

---

火炮射击

一门火炮对一个目标进行打击, 炮弹的毁伤幅员是以炸点为中心的矩形, 其纵深平行于射击方向为 $4$ 米, 正面为 $8$ 米. 目标点若位于炸点的毁伤幅员内则被毁伤. 假定火炮射击的误差在纵深方向服从方差为 $64$ 的正态分布, 在水平方向服从方差为 $25$ 的正态分布. 同时假定炮弹在纵深方向与水平方向的落点互不干扰. 问:
(1) 该门火炮瞄准目标时, 发射一枚炮弹即可摧毁该目标的概率？
(2) 若要以 $95\%$ 的概率击毁该目标, 至少应该发射几枚炮弹？

---

解:

(1) 以目标为原点建立坐标系. 假定炮弹的落点坐标为 $(x, y)\in\mathbb{R}^2$, 若该目标被毁伤, 则炮弹的落点范围需落在区域 $D=\{-4\leq x\leq 4, -2\leq y\leq 2\}$ 内.

故该目标被摧毁的概率为

$$\begin{aligned} P\{(X,Y)\in D\}&=P\{-4\leq X\leq 4, -2\leq Y\leq 2\}\\ &=P\{-4\leq X\leq 4\}P\{-2\leq Y\leq 2\}\\ P\{-4\leq X\leq 4\}&=P\{X\leq 4\}-P\{X\leq -4\}\\ &= P\{X/8\leq 4/8\}-P\{X/8\leq -4/8\}\\ &=\Phi(0.5)-\Phi(-0.5)=2\Phi(0.5)-1\approx 0.383 \end{aligned}$$

同理可计算得 $P\{-2\leq Y\leq 2\}=2\Phi(0.4)-1\approx 0.3108$.

综上 $P\{(X,Y)\in D\}\approx 0.119$.

---

(2) 记事件 $X=\text{目标被命中次数}$, 则发射 $n$ 枚炮弹击中目标的概率为

$$\begin{aligned} P\{目标被命中\}&=P\{X\geq 1\}=1-P\{X=0\}\\ &=1 - (1-0.119)^n\geq 0.95 \end{aligned}$$

计算可得 $n=\frac{\log(0.05)}{\log(0.881)}\approx 23.64,$ 故发射 $24$ 枚炮弹即可以 $95\%$ 的概率摧毁该目标.