第十三讲 智能计算——遗传算法

数学建模 讲义 NUDT 2023SP

---

---

13.1 什么是智能计算

• 智能计算 （计算智能，Computational Intelligence）usually refers to the ability of a computer to learn a specific task from data or experimental observation.
  
  • 例如：以生物进化的观点认识和模拟智能
  • 例如：研究在复杂多变的环境中启用或促进智能行为的自适应机制
• 在此，将智能计算视为求解非线性优化问题的若干算法的总体，主要包括：遗传算法、模拟退火算法、粒子群算法、蚁群算法、人工神经网络 等

---

传统优化算法

• 非线性优化问题一般没有确定性的通用求解方法，大多数时候都是采用迭代（最速下降、共轭梯度）求解
• 迭代的算法框架：
  
  1. 选定一个初值.
  2. 根据当前值选定一个前进方向.
  3. 确定一个前进步长.
  4. 在特定的方向上前进一定的步长，得到新的当前值，如果满足迭代终止条件则结束，否则转 2.

---

迭代算法的主要不足

• 不同迭代算法的区别主要在于初值、前进方法和前进步长的选取方法不同.
• 选取方向、确定步长时，一般需要利用目标函数的解析性质，比如：连续性、可微性等，如果函数不具备这些性质，则无法使用这些方法求解.
• 这些方法主要的缺点是容易陷入局部极值点.
  
  • 当求得一个局部极值后，算法往往会中止.

---

智能计算算法的特点

1. 模拟或参考某种自然现象或物理过程，对问题的要求较低，目标函数的形式更灵活
   
   • 算法可求解的问题的范围比较大，可以求解很多有趣的问题
   • 各种不同的问题可以使用相同的求解策略
2. 算法都包含 随机选取，随机生成 等操作，因此结果有一定的随机性
   
   • 算法有跳出局部最优解的能力，对于复杂问题，所得到的结果往往比传统方法得到的解更优
3. 算法的速度，解的最优性往往没有保证

---

13.2 遗传算法与进化论

• 遗传算法（进化算法/计算，Genetic Algorithm, GA）是一类模拟自然选择和遗传学机理的计算模型，是一种通过模拟自然进化过程搜索最优解的方法.
• 20 世纪六、七十年代，美国密歇根大学的 John Holland 和他的学生提出了遗传算法最初的框架
• 经过几十年的发展，各种类型的遗传算法越来越多，并且被应用于许多领域，是最重要的优化算法之一

---

自然界的进化过程

• 物竞天择，适者生存
  
  • 只有生存能力强，能够适应环境的个体才能够幸存下来，并通过交配、繁殖，将其有利于物种生存的基因遗传给后代
  • 个体的基因有可能发生变异
  • 经过自然选择过程，对物种生存有利的变异累积下去，不理想的变异则被淘汰

---

Darwin vs Lamarck

• Charles Robert Darwin，1809-1882：遗传变异、自然选择
• Chevalier de Lamarck，1744-1829：用进废退、获得性遗传
  
  • 用进废退：经常使用的器官会逐渐发达，不使用的器官会逐渐退化
  • 获得性遗传：后天获得的性状是可以遗传的，因此生物可以把后天锻炼的成果遗传给下一代
  • 强调外界环境是生物发生变异的主要原因，并对生物进化有巨大推动作用

---

现代观点

• 一直以来，分子遗传学表明，生物的性状功能无论再常用或不常用，也不会编码到染色体中
• 但是，现代生物学研究发现确实有些后天获得的特征可以传给下一代.
• 表征遗传学（Epigenetics）：DNA 甲基化和组蛋白修饰；因为生物存在某“偏好”，导致病毒对基因的修改被遗传下来.
• 目前演化生物学界仍在争论对这些机制在生物演化中的重要性，但新的发现表明：Lamarck 的学说在一定程度上，是正确的.

---

模拟自然界的进化

• 迭代与演化
  
  • 物种的变异与自然界的选择是两个独立的过程，二者交替进行，周而复始
  • 变异随机发生，从而在遗传的基础上，产生出各种不同的可能
  • 自然界（系统）对已经出现的个体进行选择，但不直接决定变异的内容和方向

---

13.3 遗传算法的原理与实现

$$\boxed{\begin{array}{c|l} 生物学 & 遗传算法\\ \hline 个体 & 算法处理的最基本对象，即一个可行解 \\ 种群 & 不断进化的对象，即一组可行解 \\ 基因 & 个体的特征，是可行解的编码形式 \\ 交叉 & 两个父代个体交换部分基因，生成子代个体，用于产生新的可行解 \\ 变异 & 某些基因的随机变化，用于产生新的可行解 \\ 反转 & 某段基因的反转，用于产生新的可行解 \\ 适应度 & 个体对环境的适应程度，相当于可行解与目标的匹配程度 \\ 选择与淘汰 & 根据适应度值，保留种群中的优胜个体（可行解），去掉较差的 \end{array}}$$

---

遗传算法的基本框架

1. 确定编码方式，随机生成初始种群；
2. 迭代直到满足终止条件：
   
   • 计算种群中每个个体的适应度函数值，通过选择淘汰不适应的个体；
   • 以一定概率通过交叉生成新的个体；
   • 以一定概率对新的个体进行变异、反转等操作；
   • 产生出下一代的种群.

---

遗传算法的实现细节

• 解的表达：个体（可行解）的编码方式
• 解的选择：
  
  • 构造适应度函数
  • 确定选择（淘汰）的策略
  • 注：两者通常是相互联系的
• 新解的产生：
  
  • 交叉、变异、反转等操作的具体实现方式

---

1. 编码

• 遗传算法本质上是在个体（可行解）构成的空间中进行搜索，编码就是可行解具体的表示形式
• 编码在设计遗传算中的作用体现在：
  
  1. 编码决定了个体的排列形式，从而决定了选择、交叉和变异等操作的进行方式
  2. 编码方法的好坏直接决定了交叉与变异等遗传操作的计算效率和执行难度，从而直接影响遗传算法运行的效率
  3. 编码决定了问题求解的精度，一个好的编码方法应该具有保持解空间拓扑连续性的特点（即：相似的解具有相似的编码）

---

常见的编码方案

• 遗传算法的编码方案有很多，最常见的是二进制串编码方式
  
  • 二进制编码（binary encoding）：以二进制字符 0 与 1 为基本单元的定长字符串编码
  • 格雷码（Gray coding）：为了弥补二进制码不能保持可行解空间连续性的缺陷而提出的编码方式
  • 实数编码，用一个 $n$ 维实数向量对个体进行编码
• 无论哪种方案，都应尽量保持个体的编码长度固定，避免使用不定长编码，减少程序设计难度

---

二进制编码

• 二进制字符串可对应于二进制整数，经过变换之后，可与一定精度的实数对应
• 优点：通用、简明、易于各种进化操作
  
  • 与十进制以及英文字母相比，在执行交叉和变异操作时更为简便
• 不足：可能破坏可行解空间的拓扑连续性，两个在解空间上非常接近的解，在编码后可能相隔非常远
  
  • 比如，在 0 到 15 的整数集中，7 与 8 是邻近的，但是其 4 位二进制编码分别为 0111 和 1000，差异（编辑距离）较大

---

格雷码（Gray code）

• 格雷码弥补了二进制码不能保持可行解空间连续性的缺陷
• 格雷码在形式上仍然是二进制字符串，是二进制编码的一种变形
• 但是，格雷码在连续的两个相邻整数之间所对应的编码值之间仅有一个码位不相同，其他码位完全相同

$$\boxed{\begin{array}{c|c|c} 十进制整数 & 标准二进制码 & 格雷码 \\ \hline 0 & 0000 & 0000 \\ 1 & 0001 & 0001 \\ 2 & 0010 & 0011 \\ 3 & 0011 & 0010 \\ 4 & 0100 & 0110 \\ 5 & 0101 & 0111 \\ 6 & 0110 & 0101 \\ 7 & 0111 & 0100 \\ 8 & 1000 & 1100 \\ 9 & 1001 & 1101 \\ 10 & 1010 & 1111 \\ 11 & 1011 & 1110 \\ 12 & 1100 & 1010 \\ 13 & 1101 & 1011 \\ 14 & 1110 & 1001 \\ 15 & 1111 & 1000 \end{array}}$$

---

标准二进制编码与格雷码的互转

• 设某一整数的二进制编码为：$B=b_n b_{n-1} \ldots b_2 b_1$，格雷码为：$G=g_n g_{n-1} \ldots g_1$，$\oplus$表示异或运算（不带进位的二进制加法）

• 二进制编码转格雷码：$\left\{\begin{array}{l} g_n = b_n, \\ g_i = b_i \oplus b_{i+1}, i = n-1,\ldots, 1 \end{array}\right.$

• 格雷码的最高位与二进制编码相同，其余各位是二进制编码中对应位和其左边一位的异或值

• 格雷码转二进制编码：$\left\{\begin{array}{l} b_n = g_n, \\ b_i = g_i \oplus b_{i+1}, i = n-1, \ldots,1 \end{array}\right.$

• 二进制编码的最高位与格雷码相同，其余各位是格雷码对应位与其左边一位对应的二进制编码的异或值

---

2. 适应度函数

• 为了确定一个遗传算法中个体的生存能力，需要用某个函数来量化其所对应的可行解究竟有多好，这个函数就是 适应度函数（Fitness Function）
• 适应度函数将个体的编码映射为一个标量值，比如，如果用 $n$ 维向量对个体进行编码，那么适应度函数可以表示为：$f:\boldsymbol{X}^n\to \mathbb{R}$
• 适应度函数通常赋予优秀的个体较大的适应度值，劣质的个体较小的值
  
  • 优化的目标是寻找适应度函数值尽可能大的个体
  • 选择规则可能对适应度函数有一定的要求（例如要求适应度函数非负）

---

与优化目标函数的联系与区别

• 原问题的优化目标是构造适应度函数的基础，适应度函数可以视为优化目标的一种具体表现形式
  
  • 两者在形式上不要求完全相同，但优化方向必须一致
  • 如果原问题有明确的目标函数，并且满足遗传算法对适应度函数的要求，可以直接作为适应度函数
• 适应度函数与原问题的优化目标函数不是两个完全相同的概念
  
  • 原问题的优化目标可能是模糊的、笼统的、难以计算的
  • 但适应度函数必须明确、具体、可计算（但不一定要有解析表达式）

---

3. 选择规则

• 选择的主要目的在于使当前种群中优良的个体拥有更多的机会繁衍后代，以便将其优质基因传递下去
• 同时，选择规则还应该保证种群始终具有一定的多样性，即以一定的概率保留一部分相对较差的个体
  
  • 目的在于使算法具有跳出局部最优解的能力，避免算法早熟而收敛到次优解
• 常见的选择方法包括：比例选择法 (轮盘赌选择法)、锦标赛选择法、精英选择法、排序选择法

---

比例选择法（轮盘赌选择法）

• 比例选择法按个体的适应度大小占总适应度的比例确定选择概率
• 设种群中有 $n$ 个个体，适应度函数为 $f$
• 个体 $\boldsymbol{x}_i$ 的适应度为 $f(\boldsymbol{x}_i)$，则其被选中的概率为：$P(\boldsymbol{x}_i)={f(\boldsymbol{x}_i)}\bigg/{\sum\limits_{j=1}^n f(\boldsymbol{x}_j)}$
• 这里要求适应度函数 $f$ 是非负的，并且适应度越大表示个体越优良
• 不足：选择与适应度成正比，导致较强个体的子代可能在子代中主导地位更强，影响种群的多样性

---

锦标赛选择法

• 锦标赛选择法每次从种群中随机选择 $m\;(m<n)$ 个个体作为一组，相互比较，保留其中最好的个体
• 需要选出多少个个体，以上操作就进行多少次
• $m$ 的取值应该适中
  
  • $m$ 越大，当前种群的最优个体越容易主导种群的发展
  • $m$ 越小，选中不良个体的概率就越大，可能影响进化的效率

---

精英选择法

• 精英选择法确保当前种群中一定比例的最优个体能存活到下一代，最优个体不经过变异，直接复制到新种群中
• 每次直接复制到下一代的个体越多，种群的多样性就越少

排序选择法

• 根据个体的适应度，由大到小对种群进行排序，指定其序号，然后按照事先设计好的概率表按序分配给个体，作为各自的选择概率
• 选择概率与适应度没有直接关系，而仅与次序有关，序号越大，被选中的概率越低，递减的速度视问题的需要指定
• 选择概率与序号的关系需要事先确定

---

4. 新个体（可行解）的产生方式

• 产生新解的方法一般统称为 遗传算子（Genetic Operator）
• 常见的遗传算子：交叉、变异、反转
• 以下讨论均以二进制字符串编码方式为前提

---

交叉

• 交换两个个体的一部分基因，以生成新个体
  
  • 在遗传算法中，交叉是应用最普遍的遗传算子
• 单点交叉：在个体串中随机选定一个交叉点，将两个父代个体该点前后的子串进行互换，生成两个新个体. 比如：
  
  • $\mbox{个体 A：}1001|111\rightarrow 1001000\mbox{：新个体 A'}$
  • $\mbox{个体 B：}0011|000\rightarrow 0011111\mbox{：新个体 B'}$
• 两点交叉：随机选择两个交叉点，交换两个交叉点之间的一段. 比如：
  
  • $\mbox{个体A：}10|0111|1\rightarrow 1011001\mbox{：新个体A'}$
  • $\mbox{个体B：}00|1100|0\rightarrow 0001110\mbox{：新个体B'}$

---

变异

• 个体中某一个或某几个基因以一定的概率随机发生变动
  
  • 比如：$\mbox{个体A：}1\underline{0}011\underline{1}1\rightarrow 1101101\mbox{：新个体A'}$

反转

• 在一个个体的编码中随机挑选两个反转点，将两个反转点之间的基因逆序，从而实现基因的重排
  
  • 比如：$\mbox{个体A：}10|0111|1\rightarrow 1011101\mbox{：新个体A'}$

---

5. 终止条件

常用的终止条件：

• 找到最优解
• 种群达到指定的代数
• 消耗完预算（如：计算时间、费用）
• 适应度稳定在一定范围，迭代不能进一步提高适应度
• 手工确定
• 以上条件的各种组合

---

13.4 遗传算法应用实例

---

1. 可微函数的最值问题

求一元函数

$f(x)=x\sin(10\pi x)+2$

在区间 $[-1,2]$ 上的最大值.

• 数值解：最大值约为 3.85，最大值 $x=1.85$ 附近

---

编码

• 区间 $[-1,2]$ 中每一个实数值都是问题的一个潜在的可行解
• 由于精度的限制，只能取满足一定精度要求的一个子集，比如要求精确到 6 位小数
• 对这个子集中的每一个点，既可以使用二进制字符串编码，也可以直接使用一个浮点数进行编码
• 以下采用标准二进制字符串编码

---

二进制编码的长度

• 如果要求精确到 6 位小数，考虑到区间长度为 $3$，所以至少要将区间分为 $3/0.000001=3\times 10^6$ 等份
• 又因为长度为 $n$ 的二进制字符串可以构成 $2^n$ 个不同编码，并且 $2097152=2^{21}<3\times 10^6<2^{22}=4194304$
• 因此编码的二进制字符串长度至少为 22 位

---

编码转换

• 一个 22 位的二进制字符串可以视为一个 22 位的二进制整数 $b$，使用下面的公式可以将 $b$ 映射为区间 $[-1,2]$ 上精确到 6 位小数的实数：
  
  • $x=-1+b\cdot \frac{2-(-1)}{2^{22}-1}$
• 而区间 $[-1,2]$ 上精确到 6 位小数的实数 $x$，使用下面的公式编码为 22 位二进制整数 $b$
  
  • $b=\mbox{round}{\left(\frac{2^{22}-1}{2-(-1)}\cdot(x+1)\right)}_2$，其中 round 表示四舍五入函数
• 例如：0000000000000000000000 对应 -1.000000，1111111111111111111111 对应 2.000000， 1001100101110011010011 对应 0.798247

---

其他要素

• 适应度函数：由于 $f(x)$ 在区间 $[-1,2]$ 上非负，并且是求最大值，因此可直接使用 $f(x)$ 作为适应度函数
• 选择规则：比例选择法
• 交叉采用单点交叉方式
• 加入一定比例的变异、反转等操作

---

计算结果

• 取种群规模为 50，交叉概率 0.75，变异概率 0.10，代数上限 200
• 某一次计算所找到的最佳个体为：
  
  • $b^*=1111001101000000001010$
  • $x^*=1.850594$
  • $f(x^*)=3.850272$
• 实际：$f_{\max}=f(1.85)=3.85$

---

---

---

关于结果的说明

• 初始种群是随机生成的，基本上均匀分布在 $[-1,2]$ 整个区间上
• 前几代迭代的效果不太明显，但种群的分布呈现出整体向右侧移动的趋势
• 经过 20 代左右，种群多数个体已经聚集在最优值附近
• 迭代过程中，种群始终保持了一定的多样性

---

收敛速度与平均适应度

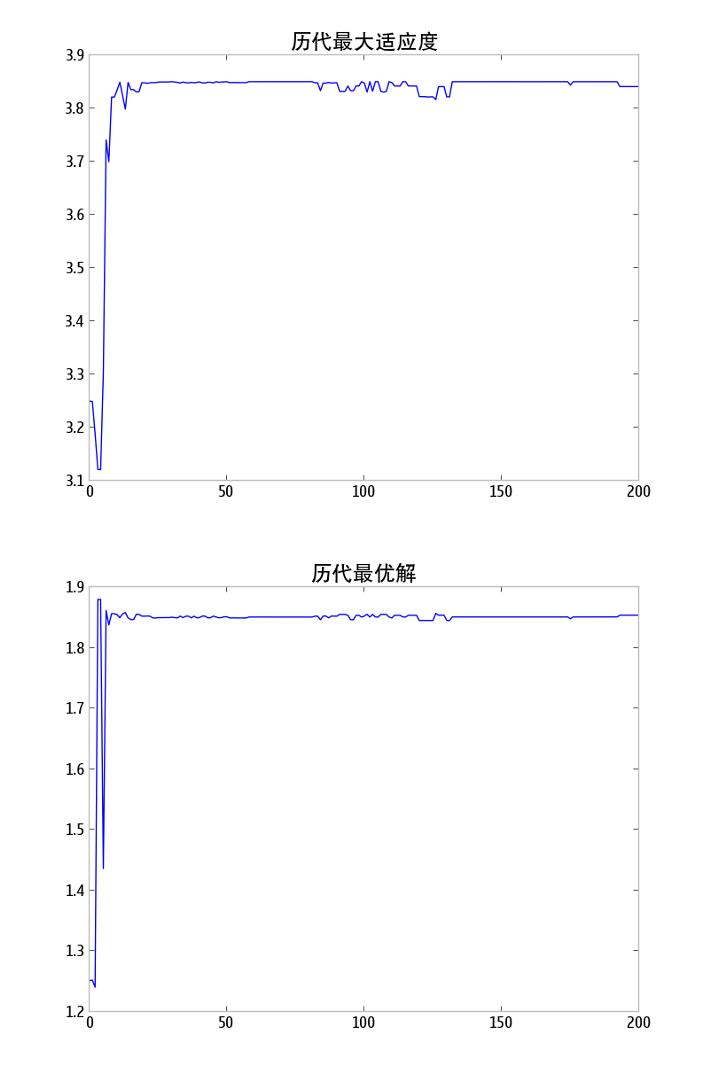
• 从历代最大适应度曲线可以看出，在这个例子中，算法收敛的速度比较快，结果比较稳定
• 每一代的平均适应度也是衡量算法优劣的一项指标

---

2. 求解"十滴水"游戏

---

游戏规则

• 在 $6\times 6$ 大小的盘面上，随机分布 4 种大小不同的水珠若干，每个水珠分别包含 1-4 滴水 (对应地称为一到四级水珠)
• 游戏开始时提供 10 滴水，每次可向一个水珠加 1 滴水，使水珠变大一级
• 如果给四级水珠再增加 1 滴水则会使其爆裂为 4 个水滴，并向四个方向飞溅
• 每个飞溅出来的水滴碰到的水珠也会升一级或爆裂，以此类推
• 当盘面上所有水珠被消除即可进入下一关
• 当所有水滴都用完，盘面上仍有水珠没有被消除，则游戏结束

---

附加规则

• 奖励机制或积分系统 [可选]
  
  • 例如，如果点击一次连续消除了多个水珠，则系统会根据连续消除水珠的数量多少奖励若干滴水，或者，每次过关时奖励 1 滴水
• 由于奖励机制和积分规则不统一，以下只考虑游戏的基本规则
  
  • 即，对于给定的游戏开局，求解过关策略，使得过关所用的水滴最少（点击次数最少），不考虑奖励的水滴或积分

---

问题的特点

• 不是常规的优化问题，难以转化为经典的规划问题
• 盘面的尺寸不是太大，当最少过关水滴数较小时，穷举搜索法能够较快的得到问题的最优解，甚至是全部的最优解
• 搜索空间随着水滴数成指数级增长，搜索法对于需要较多水滴才能完全消除的局面，求解速度会非常慢，很可能在有限的时间内给不出一个可行解

---

用遗传算法求解

• 能否使用遗传算法求解，取决于遗传算法所需的要素能否实现，其中，编码和适应度函数是关键
  
  • 编码：一个潜在的可行解就是一个点击（位置）序列，实际操作时只需按照该序列在盘面上依次加水（点击）
  • 适应度函数：给定一个点击序列，可以通过模拟点击判断按照此序列操作能否将全部水滴消除，以及需要多少步
    
    • 该函数没有解析表达式

---

编码

• 使用方阵 $\boldsymbol{A}=[a_{ij}]_{6\times 6}$ 记录当前的盘面信息，其中 $a_{ij}\in\{0,1,2,3,4\}$ 表示在第 $i$ 行第 $j$ 列的位置中的水（滴数）量
• 每个位置可以记录为 $(i,j)$，其中 $i,j=1,...,6.$
• $(i,j)$ 出现在序列的第 $k$ 个位置表示第 $k$ 步点击该位置（在该位置加水）
• $l$ 次点击的序列可记为长度为 $l$ 的向量：$\bbox[yellow]{\boldsymbol{c}=[(i_1, j_1),(i_2, j_2),\ldots,(i_l, j_l)]}$
• 另一种编码方式：将每个位置记录为一个两位整数 $ij$，于是点击序列 $\boldsymbol{c}=[i_1 j_1, i_2 j_2, \ldots, i_l j_l]$

---

适应度函数

• 按照点击序列的顺序，依次模拟每次点击后盘面的变化情况，根据最终的结果，评价该点击序列的优劣
• 最终可能出现的情况只有两种：
  
  1. 依次点击 $k$ 次（$k\leqslant l$）后，盘面被清空.
  2. 依次点击 $l$ 次后，盘面上仍然剩余 $r$ 个水珠.
• 对于第一种情况，显然 $k$ 越小越好，或者说 $l-k$ 越大越好.
• 对于第二种情况，一般来说，可以认为 $r$ 越小越好.

---

适应度函数的定义

$$f(\boldsymbol{c})=\left\{ \begin{array}{ll} l-k, & \mbox{情况 1：盘面被清空} \\ -r, & \mbox{情况 2：余下了 } r \text{ 个水珠} \end{array} \right.$$

• 适应度函数 $f$ 是一个取值为 $-36$ 至 $l-1$ 之间所有整数的函数
• 如果后续希望使用比例选择法，可以通过平移 $f'=f+37$ 将适应度变换为非负函数

---

当前适应度函数的缺陷

• 当出现情况 2 时，清除盘面上剩余水珠所需要的水滴数，不只是与水珠的数量有关，还与水珠的位置分布以及饱满程度有关
• 为解决这一问题，除了可以修改 $f$ 的定义，针对情况 2 设计更有区分度的指标以外，还可以简单的增大 $l$ 来解决
• 适应度函数明确、具体、可计算，但是可直接用于计算的解析表达式，只能模拟完成点击来得到结果
• 模拟点击过程是求解的关键，也是相对复杂的部分，算法实现需要考虑的细节比较多

---

选择规则

• 考虑到前述 $f$ 的缺陷，以及适应度函数值的实际含义，这里不考虑使用比例选择法
• 使用 改进的精英选择策略
  
  • 适应度最高的一定比例的个体直接进入下一代，为保证种群的多样性，再从后面的个体中随机选择一定比例进入下一代
  • 已入选的个体交叉生成剩余数量的个体，再进行变异、反转等操作

---

变异

• 随机选定一个变异点后，将该点所对应的坐标，随机向上、下、左、右四个方向中的一个方向移动一步或两步
  
  • 如果移动会导致出界，可以认为是移动到盘面的另一侧
  • 也可以设计为向周围 8 个方向变化，并引入对应的越界处理方法

反转

• 选定两个反转点后，将两点之间的序列反转即可

---

实现中的几个问题

• 如果某一个体的适应度为 $l-k$ 大于 0，说明它只需要 $k$ 滴水就能清空盘面，则该个体在参与交叉、变异或反转时，位置点的选择需要
  限定在前 $k$ 个元素进行
• 适应度函数值最大为 $l-1$，因此如果找到适应度为 $l-1$ 的个体，就是找到了最优解，算法可以停止
• 坐标可以改为从 0 开始计数，即 $i,j$ 的取值范围不是 1-6，而是 0-5。这样便于处理出界的情况，也与很多程序设计语言的习惯一致

---

总结

对于十滴水游戏，使用遗传算法求解有以下特点：

• 不是一个常规的优化问题，很难使用传统优化模型来刻画和求解
• 当 $l$ 比较小时，没有暴力搜索法速度快，但当 $l$ 比较大时，算法优势明显，可以在相对较短的时间内给出令人满意的解，虽然并不能保证是最优解
• 适应度函数是通过模拟点击来实现的，而不是计算得到，与常见的遗传算法不同
• 算法灵活，计算适应度时，很容易加上对奖励和积分系统的处理

---

遗传算法在数学建模竞赛中的应用

美赛中，很多题目可以使用遗传算法求解，并且这些题目几乎都是侧重于设计的优化问题：

• 2003 年 B 题，Gamma 刀治疗方案
• 2003 年 C 题，机场安检问题
• 2006 年 A 题，喷淋灌溉系统的布局与移动问题
• 2007 年 B 题，登机顺序问题
• 2008 年 B 题，数独游戏设计问题
• 2009 年 A 题，交通环岛信号灯设计问题
• 2011 年 A 题，滑雪道设计

---

相关文献：

• Fei S, Lin Y, Hong W. The Genetic Algorithm-Based Optimization Approach for Gamma Unit Treatment[J]. MAP Journal, 2003, 23(3): 323–338.
• Michelle R. Livesey, Carlos A. Diaz, Terrence K. Williams. Advancing Airport Security through Optimization and Simulation[J]. UMAP Journal, 2003, 24(2): 141–152.
• Dunham B, Francischetti S, Nixon K. Sprinkler Systems for Dummies: Optimizing a Hand-Moved Sprinkler System[J]. UMAP Journal, 2006, 27(3): 237–254.
• Li Q, Mehta A, Wise A. Novel Approaches to Airplane Boarding[J]. UMAP Journal, 2007, 28(3): 353–370.
  Mantere T, Koljonen J. Solving and rating sudoku puzzles with genetic algorithms[C]//New Developments in Artificial Intelligence and the Semantic Web, Proceedings of the 12th Finnish Artificial Intelligence Conference STeP. 2006: 86–92.
• Zhu Z A, Mao T, Huang Y. Three Steps to Make the Traffic Circle Go Round[J]. UMAP Journal, 2009, 30(3): 261–280.
• Gong E, Wang X, Li R. A Half-Blood Half-Pipe, A Perfect Performance[J]. UMAP Journal, 2011, 32(2): 109–122.

---

Gamma 刀治疗方案 — MCM 2003 B

• 立体定位放射外科，用单一高剂量离子化射束在 X 光机精确界定下照射颅内的一个小的 3D 脑瘤，与此同时，不能以任何显著的处方剂量伤及周边的脑组织
• 一般有三种形式的射束可以采用，分别是 Gamma 刀单元，带电重粒子射束，以及来自直线加速器的外用高能光子束
• Gamma 刀单元具备的单一高剂量离子化射束，是 201 个钴-60单位源通过厚重的盔状物发射出来的
• 所有的 201 条射束同时交会于一个中心 (最大放射剂量点)，从而在有效剂量的水平上形成一个近似球形的剂量分布
• 照射这个中心来达到处方剂量称为一个 shot

---

参数说明

• 多个 shot 可以表述为不同的球（大小和中心可能不同）
• 四个可以互换的外部校准的盔状物分别具有 4，8，14 和 18mm 的射束通道直径，都可以用来照射不同尺寸的体积
• 对于大于一个 shot 的目标体积，可以用多个 shot 来覆盖整个目标
• 实际上，大多数目标体积要用 1 到 15 个 shot 加以处理
• 在这里，目标体积是一个有界的通常包含数百万个点的三维数字图像

---

对治疗方案的要求

• 放射外科强调消除肿瘤细胞同时保存正常的结构
• 由于治疗过程中会涉及物理限制和生物不确定性，一个治疗方案就需要考虑到所有那些限制和不确定性，为此一般提出如下的要求
  
  • 穿过目标体积的剂量梯度最小
  • 为目标体积配置特异性的相同剂量轮廓线
  • 为目标和关键器官配置特异性的剂量—体积限制条件
  • 对正常组织或器官的整个体积照射要剂量总和最小
  • 对指定的正常组织点的剂量要限制在忍耐剂量以下
  • 使关键体积所需的最大剂量达到最小

---

Gamma 单元治疗方案的附加限制

• 禁止 shot 伸展到目标以外
• 禁止 shot 交迭（避免热点）
• 用有效的剂量覆盖尽可能多的目标体积，至少 90% 目标体积要被 shot 覆盖
• 用尽可能少的 shot
• 任务：用球体填充问题模型来建立最优的 Gamma 刀治疗方案，并且提出一个求解的算法. 在设计算法时你要记住: 它必须是相当有效率的.

---

为什么使用遗传算法进行求解？

• 很难直接求解出满足各种约束的最优的方案
  
  • 甚至约束条件的显式的数学表达式本身就很难写出
• 不同 shot 数、不同直径、不同位置的组合非常多
• 如果给定一种组合，评价其优劣是相对比较容易的
• 问题另外一个困难在于多目标之间的平衡

---

13.5 遗传算法的适用范围和优缺点

• 遗传算法与经典优化算法的主要区别在于搜索过程不同，引导搜索方向的信息不同
  
  • 搜索过程：经典优化算法使用确定的规则，从解空间中的一点移动到另一点，搜索过程只能顺序进行；遗传算法根据概率进行移动，移动方向不确定，并且可以从多个初始点开始搜索，搜索过程可以并行进行
  • 引导信息：经典优化算法一般需要使用导数信息来确定搜索方向；遗传算法的搜索只依赖于个体的适应度，适应度函数不必使用导数信息.
• 总体上，经典的优化算法在求解线性规划、二次规划，以及其他某些特定问题时更有优势；遗传算法对于非连续、不可微和带噪声的问题则更有效.

---

遗传算法的优缺点

• 优点：

  • 提供了一种通用的求解框架，适用范围较广
  • 不需要导数等信息
  • 有一定的跳出局部最优解的能力
  • 容易并行求解
  • 容易与其他方法结合

• 不足：

  • 设计合适的编码方式和适应度函数一般比较困难
  • 对于大规模问题，速度较慢
  • 结果的最优性一般没有保证

---

遗传算法的适用范围

• 如果问题有精确的、效率高的确定性解法，优先考虑使用该解法
• 如果问题具备以下特征，可以尝试使用遗传算法：
  
  • 解空间比较明确，但规模较大
  • 问题没有直接解法或直接解法计算量过大
  • 对每一可行解，容易进行编码，并且容易评价其优劣

---

课后思考

（$\star\star$）使用遗传算法或模拟退火算法求解下列优化问题：求一元函数 $f(x)=x^2\sin(30 x)+1.5$ 在区间 $[-1, 2]$ 上的最大值.