壳层定理

Blog

---

来源：维基百科Shell theorem和殼層定理

gfield

经典力学里，牛顿给出和证明了壳层定理：

• 考察球对称质量均匀分布的物体与球体外一物体之间的万有引力，可以将球对称物体质量视为集中于球心。
• 球对称质量均匀分布的物体与其内部的物体之间的万有引力为0。

下面给出证明。

球对称质量均匀分布的物体与球体外一物体之间的万有引力

我们考察一个均匀实心球体与球外距离球心$r$处一质点$m$之间的万有引力。球体可以视为无穷多极薄的同心球壳所组成，如果每个球壳与$m$的万有引力与一个位于球壳球心处的质点与$m$的万有引力完全相同，则球体与$m$之间的万有引力也可以视为一个位于球心的质点与$m$的万有引力。下图为半径为$R$的球壳。

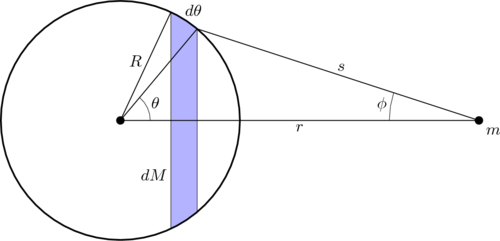
球体可划分为无数极薄的同心球壳，图为半径为$R$的球壳。注$d\theta$为无穷小角度，非弧长，弧长为$Rd\theta$

把球壳划分为无数薄圆环，即图中阴影部分，薄圆环上各点与$m$的距离为$s$。薄圆环质量为

$$\begin{equation} dM=\frac{M}{4\pi R^2}2\pi R^2 \sin\theta d\theta=\frac{M}{2} \sin\theta d\theta \label{massring} \end{equation}$$

薄圆环上 各部分与$m$的万有引力的合力将指向球壳中心，即

$$\begin{equation} dF_r=\frac{Gm}{s^2}dM\cos\phi =\frac{GmM}{2}\frac{\sin\theta \cos\phi }{s^2} d\theta \label{dFr} \end{equation}$$

积分，得球壳与$m$之间的万有引力为

$$\begin{equation} F_r=\int dF_r =\frac{GmM}{2}\int \frac{\sin\theta \cos\phi }{s^2} d\theta \label{Fr} \end{equation}$$

根据余弦定理，

$$\begin{equation} \cos\phi = \frac{r^2+s^2-R^2}{2rs} \label{cosphi} \end{equation}$$

$$\begin{equation} \cos\theta = \frac{r^2+R^2-s^2}{2rR} \label{costheta} \end{equation}$$

对$\eqref{costheta}$两边微分，

$$\begin{equation} \sin\theta d\theta = \frac{s}{rR}ds \label{dtheta} \end{equation}$$

将$\eqref{dtheta}$和$\eqref{cosphi}$代入$\eqref{Fr}$，得

$$\begin{equation} \begin{split} F_r=&\frac{GmM}{2}\int_0^{\pi} \frac{\cos\phi }{s^2}\sin\theta d\theta \\ =& \frac{GmM}{2rR}\int \frac{\cos\phi }{s}ds \\ =&\frac{GmM}{4r^2R}\int_{r-R}^{r+R} \left ( 1 + \frac{r^2-R^2 }{s^2} \right ) ds \\ =&\frac{GmM}{r^2} \end{split} \label{intFr} \end{equation}$$

可见，球壳与$m$的万有引力可以视为一个位于球壳球心处的质点与$m$的万有引力。

$\eqref{intFr}$式中的积分限如下图所示：

最后，将质量为$dM$的无限薄球壳与$m$的万有引力积分（这里要注意符号的意义，前面$M$为球壳质量，$dM$为薄圆环质量元的质量，以下$M$是实心球质量，$dM$为薄球壳质量元的质量），可得实心球与球外质点的万有引力。

$$\begin{equation} F_{total}=\int dF_r =\frac{GmM}{r^2}\int dM \label{Ftot} \end{equation}$$

半径为$x$，厚度为$dx$的球壳的质量为

$$\begin{equation} dM=\frac{M}{\frac{4}{3}\pi R^3}4\pi x^2 dx = \frac{3Mx^2}{R^3} dx \label{massshell} \end{equation}$$

代入$\eqref{Ftot}$，得

$$\begin{equation} F_{total}=\int dF_r =\frac{3GmM}{r^2R^3}\int_0^R x^2 dx=\frac{GmM}{r^2} \label{Ftotal} \end{equation}$$

可见，实心球对球外质点的万有引力与将球质量集中于球心所得的质点与球外质点的万有引力完全相同。

球对称质量均匀分布的物体与其内部的物体之间的万有引力

空心球壳质量为$M$，与其内部一质点之间万有引力由$\eqref{intFr}$式来计算，只是积分限有所变化，由下图可知，积分限为$R-r$和$R+r$：

$$\begin{equation} F_r = \frac{GmM}{4r^2R}\int_{R-r}^{R+r} \left ( 1 + \frac{r^2-R^2 }{s^2} \right ) ds =0 \label{innFr} \end{equation}$$

于是证明出，球对称质量均匀分布的物体与其内部的物体之间的万有引力为0。

推广

如果万有引力的与距离的关系为$\propto r^{-p}$，根据$\eqref{innFr}$式，球壳对球壳内部的质点的万有引力为

$$\begin{equation} F_r = \frac{GmM}{4r^2R}\int_{R-r}^{R+r} \left ( \frac{1}{s^{p-2}} + \frac{r^2-R^2 }{s^p} \right ) ds \label{innFrp} \end{equation}$$

如果要使$F_r=0$，必须要有$p=2$。