证明ln2=0 和 2=1

Blog

---

课程讲义：Be careful when manipulating conditonally convergent series

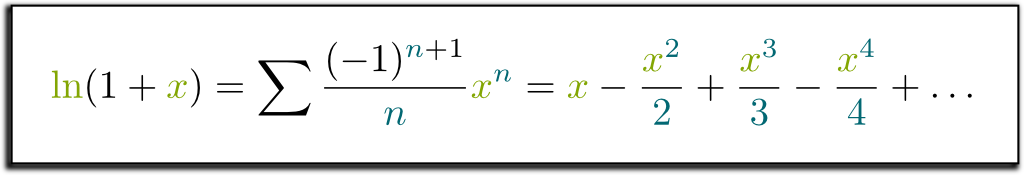
级数求和一定要注意收敛条件，否则会得到很荒谬的结论，比如可以证明 ln2=0 和 2=1

我们知道下式成立：

$$\begin{equation} \ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\ldots \label{eq1} \end{equation}$$

所以有：

$$\begin{equation} \ln 2=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots \label{eq2} \end{equation}$$

现在我们来证明 $\ln2=0$。

$$\begin{equation*} \begin{split} \ln 2 =& 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\ldots\\ =&\left (1+\frac{1}{3}+\frac{1}{5}+\ldots\right )-\left (\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\ldots\right )\\ =&\left (1+\frac{1}{3}+\frac{1}{5}+\ldots\right )+\left (\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\ldots\right )-\\ &2\left (\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\ldots\right )\\ =&\left (1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\ldots\right )-\left (1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\ldots\right )\\ =&0 \end{split} \end{equation*}$$

得证。

现在我们来证明 $2=1$。

已知：

$$\begin{equation*} \ln 2 = 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\frac{1}{9}-\frac{1}{10}+\ldots \end{equation*}$$

两边乘以 $2$，有：

$$\begin{equation*} \begin{split} 2 \ln 2 =& 2-1+\frac{2}{3}-\frac{1}{2}+\frac{2}{5}-\frac{1}{3}+\frac{2}{7}-\frac{1}{4}+\frac{2}{9}-\frac{1}{5}+\ldots \\ =&1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}+\ldots \\ =&\ln 2 \end{split} \end{equation*}$$

所以有：

$$\begin{equation*} 2 = 1 \end{equation*}$$

以上这两个荒谬的结论的证明，哪里出了问题？

问题在于 $\ln(1+x)$ 展开成的级数方程$\eqref{eq1}$不是绝对收敛的，而是条件收敛的，条件收敛的级数是不可以任意调整级数各项的位置的。