第9讲：相空间流体和吉布斯-刘维尔定理

Blog 物理理论最低基础

---

莱尼喜欢看河，尤其喜欢看漂浮物顺流而下。他猜想漂浮物如何穿过礁石，如何陷入漩涡。但是河流整体，水量，流切变，河的分流和汇聚，这是莱尼所看不到的。

相空间流体

在经典力学里，注视一个特别的初始条件，再随之在相空间走过特定轨迹，这是很自然的事情。但是还有一个更大的图像，突出强调轨迹的总集合。这个更大的图像可以直观显示所有可能的起点和所有可能的路径。不要再拿着铅笔点住相空间一点，然后沿着一条路径画线，而是做点更有雄心的事情。想象一下，你有无穷多支铅笔，用它们在相空间均匀地点点（均匀在这里的意思是在$q,p$空间点的密度处处相等）。把这些点看做假想的填充相空间的流体的组成粒子。

每个点都按照哈密顿方程运动：

$$\begin{equation} \begin{split} & \dot{q}_i=\frac{\partial H}{\partial p_i}\\ & \dot{p}_i=-\frac{\partial H}{\partial q_i} \end{split} \label{eq1} \end{equation}$$

这样，流体连绵不断地流过相空间。

谐振子是说明相空间流体的好例子。在第8讲，我们看到每个点做匀速圆周运动。（注意：我们谈的是相空间，不是坐标空间，在坐标空间，谐振子做的是一维往复运动。）整个流体做刚性运动，绕着相空间原点做匀速圆周运动。

现在我们回到一般情况。如果坐标数目是$N$，则相空间就是$2N$维的。相空间流体以特定的方式流动。流动的特点之一是，每一点的能量值——$H(q,p)$的值——始终保持不变。能量相等的点组成一个平面，比如能量值为$E$的平面由以下方程描述：

$$\begin{equation} H(q,p)=E \label{eq2} \end{equation}$$

对于每个$E$，都有一个关于$2N$个相空间变量的方程，因此可以定义一个$2N-1$维的面。换言之，每个$E$都对应一个面，所有的$E$对应的面可填充整个相空间。你可把相空间看做按方程$\eqref{eq2}$定义的等能线图，如图1。如果相空间流体的一点位于某等能面上，这点就会一直呆在这个等能面上。这就是能量守恒。

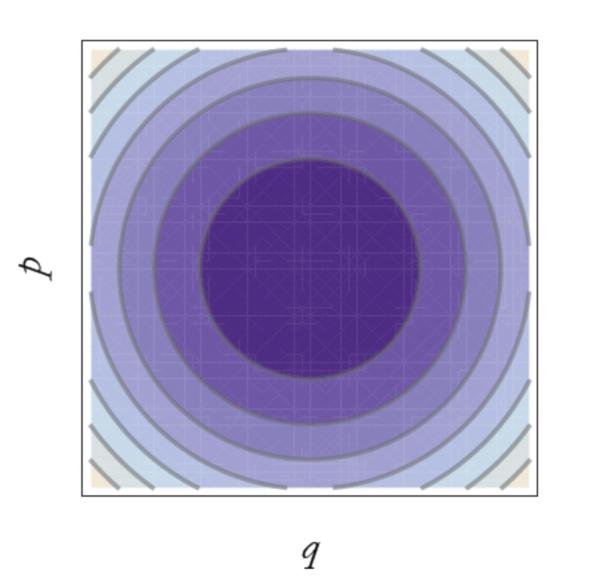
图1 谐振子等能面

对于谐振子，相空间是二维的，能量面是圆，圆的方程为：

$$\begin{equation} \frac{\omega}{2}(q^2+p^2)=E \label{eq3} \end{equation}$$

对于一般的力学系统，能量面非常复杂，无法画出来，但是原理是一样的：能量面一层一层填充相空间，相空间流体流动过程中保持各点一直呆在初始时刻所在的能量面内。

简短回顾

我们暂停一下，回顾一下第1讲的内容。在第1讲，我们讨论过硬币、色子，还有运动定律最基本的思想。我们描述这些定律用的方法，是用箭头连着表示系统状态的点，表示系统演化的过程和方向。我们还解释过，有些定律是允许的，有些定律是禁止的，可允许的定律是可逆的。可允许的定律有什么特点？答案是每个点都有一个箭头指向自己，也有一个箭头从自己指向别的点。如果有一点，指向自己的箭头多于从自己指向外部的箭头，则相应的定律是不可逆的。同样地，从自己指向外部的箭头多于指向自己的箭头，相应的定律也是不可逆的。这两种情况都是禁止的。现在我们分析一下相空间流体流动的可逆性。

流和散度

我们考虑通常空间里流体流动的几个简单的例子。暂时先忘掉相空间，只考虑通常的三维空间（坐标轴分别为$x,y,z$）的普通流体。流动可用速度场描述。空间每一点的速度矢量都标记出来，所有这些速度矢量就组成速度场$\vec{v}(x,yz)$，如图2所示。

图2. 速度场

我们还可以用速度的分量描述速度场：$v_x(x,y,z),v_y(x,y,z),v_z(x,y,z)$。一点的速度也可能是依赖时间的，但是我们只考虑不依赖时间的情况，即只考虑定常流。

我们还假设流体是不可压缩的，即一定量的流体总占据同样的体积，也即流体密度（单位体积内的分子数）是均匀的并且是保持不变的。考虑如下小立方体盒子：

$$\begin{equation*} \begin{split} & x_0<x<x_0+dx\\ & y_0<y<y_0+dy\\ & z_0<z<z_0+dz \end{split} \end{equation*}$$

不可压缩性意味着每个这么大盒子里的流体粒子数都是一定的，并且单位时间净流入盒子的流体也是0（流入流出的流体正好相等）。单位时间从面$x=x_0$流入盒子的分子数目，正比于穿过此面的流速 $v_x(x_0)$。

如果$v_x(x_0)=v_x(x_0+dx)$，则从$x=x_0$处流入盒子的流体等于从$x=x_0+dx$处流出盒子的流体。但是，如果$v_x$随位置变化，流入流出的流体就不相等，从这两个面净流入盒子的流体分子数正比于

$$\begin{equation*} -\frac{\partial v_x}{\partial x}dxdydz \end{equation*}$$

同样的道理也适用于$y_0$和$y_0+dy$，也适用于$z_0$和$z_0+dz$。把这三项都加起来，即净流入盒子的分子数为

$$\begin{equation*} -\left (\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\right )dxdydz \end{equation*}$$

括号里面的各导数有一个专门的名字：矢量场$\vec{v}(t)$的散度，记为：

$$\begin{equation} \nabla \cdot \vec{v}=\left (\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\right ) \label{eq4} \end{equation}$$

散度之名恰如其分，表示流体的分子外散而流，增大流体占据的体积。如果流体是不可压缩的，流体的体积不变，因此散度必须为0。

理解不可压缩性的一个方法是，认为流体的各分子，或是流体中的各点，都是不可压缩的，不能压缩进更小的体积，也不可以凭空消失或出现。发挥点想象力，你可以看出不卡压缩性与可逆性非常类似。在第1讲的各例子中，箭头也定义一种流。在某种意义上说，至少在可逆情况下，这种流也是不可压缩的。现在可以提出一个问题，相空间中的流动是不可压缩的吗？答案是，是的，如果系统满足哈密顿方程的话。有一个定理表述了这种不可压缩性，这个定理就是刘维尔定理。

刘维尔定理

我们再回到相空间中的流动，考虑相空间中每点流速的分量。相空间流体不是三维的，而是$2N$维的，坐标为$q_i$、$p_i$。因此速度场有$2N$个分量，$N$个$q_i$，$N$个$p_i$，分量记为$v_{q_i}$和$v_{p_i}$。

方程$\eqref{eq4}$所定义散度概念，很容易推广至任意维空间，相空间流体的散度为以下$2N$项的和：

$$\begin{equation} \nabla \cdot \vec{v}=\sum_i \left (\frac{\partial v_{q_i}}{\partial q_i}+\frac{\partial v_{p_i}}{\partial p_i}\right ) \label{eq5} \end{equation}$$

如果流体是不可压缩的，那么方程$\eqref{eq5}$比为0。要证明这一点，我们需要知道速度场的分量，即假想的相空间流体的组成粒子的速度。

相空间中任意一点的速度的分量为：

$$\begin{equation*} \begin{split} & v_{q_i}=\dot{q}_i\\ & v_{p_i}=\dot{p}_i \end{split} \end{equation*}$$

而且，$\dot{q}_i$ 和 $\dot{p}_i$正是哈密顿方程中的量，根据方程$\eqref{eq1}$，有

$$\begin{equation} \begin{split} & v_{q_i}=\frac{\partial H}{\partial p_i}\\ & v_{p_i}=-\frac{\partial H}{\partial q_i} \end{split} \label{eq6} \end{equation}$$

把方程$\eqref{eq6}$带入方程$\eqref{eq5}$，得

$$\begin{equation} \nabla \cdot \vec{v}=\sum_i \left (\frac{\partial }{\partial q_i}\frac{\partial H}{\partial p_i}-\frac{\partial }{\partial p_i}\frac{\partial H}{\partial q_i}\right ) \label{eq7} \end{equation}$$

二阶导数，如$\frac{\partial }{\partial p_i}\frac{\partial H}{\partial q_i}$，结果与求导顺序无关，因此方程$\eqref{eq7}$中括号中的两项正好抵消，因此有：

$$\begin{equation*} \nabla \cdot \vec{v}=0 \end{equation*}$$
因此，相空间中流体是不可压缩的，这在经典力学中被称为刘维尔定理，尽管与法国数学家约瑟夫·刘维尔几乎没什么关系。这个定理是美国物理学家吉布斯于1903年首先发表的，因此也称为吉布斯-刘维尔定理。

我们前面提到，流体不可压缩意味着每个小盒子的净流入量为0，这也是流体的不可压缩性的定义。这个定义还有个等价的表述。想象某个时刻一定体积的流体，这团流体可以为任何形状。追踪流体中每一点的运动，过一段时间后，这团流体就会呈现出其他形状，但是只要流体是不可压缩的，这团流体的体积就保持不变，在任意时刻的体积都与初始时刻的体积相同。因此刘维尔定理可重新表述为：任意一团相空间流体的体积都不随时间变化。

比如谐振子，相空间流体绕着原点做圆周运动，很明显任意一团相空间流体的体积保持不变，甚至它们连形状也不变。但是形状不变是谐振子的特殊性质。现在我们看另一个例子。考虑如下形式的哈密顿量：

$$\begin{equation*} H=pq \end{equation*}$$

你很可能没见过这个哈密顿量，但是这个哈密顿量完全可以存在的。我们先写出运动方程：

$$\begin{equation*} \begin{split} & \dot{q}=q\\ & \dot{p}=-p \end{split} \end{equation*}$$
解出这个微分方程组，可以看出$q$随时间指数增大，$p$以同样的速率随时间指数减小。换言之，流沿着$p$轴压缩，而沿着$q$轴膨胀，压缩的量与膨胀的量相同。每一团流体沿着$q$轴被拉伸，沿着$p$轴被挤压。很明显，流体团形状极端扭曲，但是相空间体积不变。

刘维尔定理是与第1讲中的可逆性最接近的类比。在量子力学里，刘维尔定理被代之以幺正性。

泊松括号

19世纪法国数学家思考力学的时候发明了这些极其漂亮的数学形式，他们在想些什么呢？（哈密顿例外，他是爱尔兰人）他们是如何得到作用量原理、拉格朗日方程、哈密顿量、刘维尔定理？他们是在解物理题吗？他们只是为了玩出漂亮的方程吗？还是只是为了设计新的物理原理？我认为这些因素都有一点，但在各个方面都取得了极大成功。但是这些极大的成功直到20世纪量子力学被发现之后才变得清晰。看起来好像数代人之前的数学家机具洞察力，他们发明了百年之后量子概念的等价概念。

还没完。还有一个力学形式理论，即泊松括号，以法国数学家泊松的名字命名，这好像也是个超越时代的理论。下面我们介绍泊松括号。考虑某个关于$q_i$和$p_i$的函数，这样的函数有动能、势能、角动量等等，当然还有其他各种我们可能感兴趣的物理量。我们先不指明具体函数，记为$F(q,p)$。

我们现在细致考察$F(q,p)$。首先，它是相空间中的位置的函数。但是如果我们追踪相空间中任何一点——体系的任何真实的轨迹——都对应一个函数值$F$，即$F$的值随沿着轨迹而变。换言之，体系沿着某轨迹的运动使$F$称为时间的函数。我们现在计算$F$如何随着给定一点的运动而变，即计算$F$的时间导数：

$$\begin{equation*} \dot{F}=\sum_i \left ( \frac{\partial F}{\partial q_i}\dot{q}_i+\frac{\partial F}{\partial p_i}\dot{p}_i \right ) \end{equation*}$$
代入哈密顿方程，得：

$$\begin{equation} \dot{F}=\sum_i \left ( \frac{\partial F}{\partial q_i}\frac{\partial H}{\partial p_i}-\frac{\partial F}{\partial p_i}\frac{\partial H}{\partial q_i} \right ) \label{eq8} \end{equation}$$

我也不知道泊松如何发明了他的括号，我怀疑是方程$\eqref{eq8}$的右边他写烦了，决定用新的符号简化一下。拿出两个相空间的函数，$G(q,p)$和$F(q,p)$。先不管它们的物理意义，也不管是不是其中一个是否是哈密顿量。$F$和$G$的泊松括号定义为：

$$\begin{equation} \{F,G\}=\sum_i \left ( \frac{\partial F}{\partial q_i}\frac{\partial G}{\partial p_i}-\frac{\partial F}{\partial p_i}\frac{\partial G}{\partial q_i} \right ) \label{eq9} \end{equation}$$

泊松再写方程$\eqref{eq8}$就简洁了，可写为：

$$\begin{equation} \dot{F}=\{F,H\} \label{eq10} \end{equation}$$

方程$\eqref{eq10}$神奇之处在于它的涵意极其丰富。任何物理量的时间导数都可以写为该物理量与哈密顿量的泊松括号。甚至连哈密顿方程本身也包括在内。要看出这一点，令$F$为任何一个$q$，由方程$\eqref{eq10}$，有：

$$\begin{equation*} \dot{q}_k=\{q_k,H\} \end{equation*}$$
把上式中的泊松括号写开，其实只有一项，即$q_k$对自身的求导那一项。由于$\frac{dq_k}{dq_k}=1$，于是泊松括号$\{q_k,H\}$恰好等于$\frac{\partial H}{\partial p_k}$，这正是哈密顿方程组中的第一个方程。同理，哈密顿方程组的第二个方程等价于
$$\begin{equation*} \dot{p}_k=\{p_k,H\} \end{equation*}$$

注意到在这个形式理论中，哈密顿方程组的泊松括号形式的这两个方程是同号的，$q$和$p$分别对应的方程的符号差异隐藏在泊松括号的定义里。

法国人对优雅的迷恋回报丰厚。泊松括号成为量子力学里最基本的量：对易子。