插播数学1：空间、三角、矢量

物理理论最低基础 Blog

---

“乔治，我们现在在哪里？”
乔治拿出地图，展开在莱尼面前：“我们在这里，坐标36.60709N, –121.618652W.”
莱尼问：“嘛是坐标？”

坐标

要定量描述点，我们需要一个坐标系。建立坐标系第一步是在空间选取一个点作为原点，一般要求选的原点，能使方程尽可能简单。比如，研究太阳系，原点选在太阳上，理论方程方程会很简单，如果选在其他地方，问题就会变得很复杂。严格来讲，原点可以任意选取，但是一旦选定，就不能变动了。

下一步就是选三个互相垂直的坐标轴。这三个坐标轴的位置也可以是任意的，只要互相垂直就行。一般让坐标轴交于原点。这三个轴常称为$x$, $y$ 和 $z$，也常叫做$x_1$, $x_2$, $x_3$。这种坐标系称作笛卡尔坐标系，如图1所示。

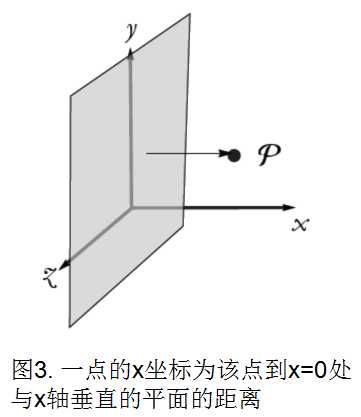
建坐标系是为了描述空间某一点，可以把这一点称为$\mathcal{P}$。由点的坐标$x$, $y$, $z$定出点$\mathcal{P}$的位置，即由三个有序数对$(x,y,z)$识别不同的点。见图2。

假想在$x=0$处放置一个平面，$x$坐标就是点$\mathcal{P}$到这个平面的垂直距离（见图3）。同理定义点的$y$和$z$坐标。由于坐标是距离，因此有长度的单位，比如米。

如果研究运动，我们还需要记录时间。时间也需要定个原点，即零时刻的时候。零时刻也可以任意选取，比如选取宇宙大爆炸发生的时刻、耶稣降生的时刻，或一个实验开始的时刻。但是一旦选定，就不能再改动了。

下一步要定义时间的方向。一般的选法是，走向未来为时间的正方向，回到过去为时间的负方向。反过来定义当然也可以，但是我们不这么做。

最后，我们需要定出时间的单位。物理学家习惯采用秒作为时间的单位，但小时、纳秒、年也可能会用到。选定好时间原点和单位，我们就可以用一个数$t$来标记时间了。

在经典力学里，我们对时间有两个隐含的假设。第一个假设是，时间均匀流逝，比如1秒的时间间隔，永远不会变。比如，重物从比萨斜塔落到地面，伽利略的时间和我们的时间是一样的。过去的1秒与现在的1秒是完全一样的。

第二个假设是，不同地点的时间可以比较。不同地方的钟可以校准之后同步运行。有了这些假设，4个坐标——$x$, $y$, $z$, $t$——就可以定义一个参考系。参考系里的任何事件都可用4个坐标予以标记。

给定一个函数，可以在坐标系里画点，比如函数$f(t)=t^2$。用一个坐标轴表示时间$t$，另外一个轴表示函数值$f(t)$，如图4。

我们用曲线把这些点连起来，填充上点之间的空间，如图5所示。

这样我们就看到了函数的样子。

练习1：用图形计算器或数学软件如Mathematica画出以下函数: $$f(t)=t^4 + 3 t^3 - 12 t^2 + t - 6$$ $$g(x) = \sin x - \cos x$$ $$\theta(\alpha)=e^{\alpha}+\alpha\ln \alpha$$ $$x(t) = \sin^2 t - \cos t$$

(注：练习1中第4个方程，原文为$x(t) = \sin^2 x - \cos x$)

三角

如果你没学过三角，或学过但忘的差不多了，可以看看这一部分。

物理学里会时时处处遇到三角。所以你需要熟悉三角里的概念、符号、方法。

在物理学里，我们一般不用度来度量角，而是用弧度，radian，$2\pi$相当于360°，$1\quad radian = 180°/\pi$，因此，$90°=\pi/2$弧度，$30°=\pi/6$弧度，因此1弧度约相当于57°，见图6.

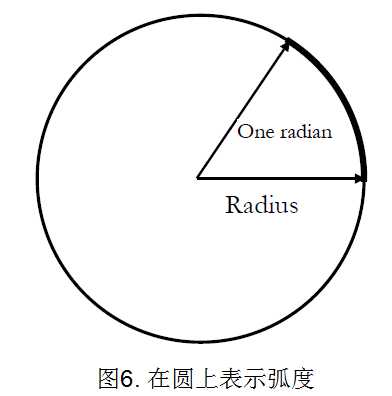
三角函数是用直角来定义的。图7为直角三角形，斜边长为$c$，底边长为$b$，高为$a$。高所对的角为$\theta$，底边所对的角$\phi$。

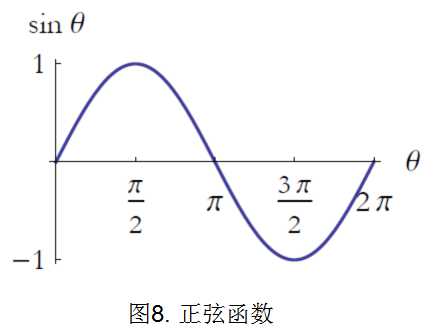
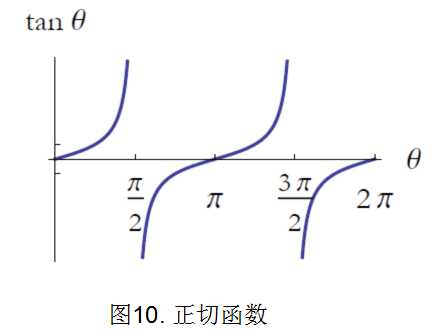
三角函数正弦、余弦、正切定义为三个边的比值，分别定义为下：

$$\sin \theta =\frac{a}{c}$$ $$\cos \theta =\frac{b}{c}$$ $$\tan \theta = \frac{a}{b}=\frac{\sin\theta}{\cos\theta}$$
这三个函数的图形见图8-10。

可以把直角三角形画在一个圆里，圆心为笛卡尔坐标系原点，如图11所示。

把原点与圆形上一点连起来，这就是直角三角形的斜边，圆形上这一点的水平和竖直分量分别是底边和高，这一点有两个坐标$x$和$y$，

$$x=c\cos\theta$$ $$y=c\sin\theta$$
直角三角形和圆的这个关系非常有用。

两角$\alpha$和$\beta$和与差的三角函数与$\alpha$和$\beta$的三角函数有如下关系：

$$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$$ $$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$$ $$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$$ $$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$$

还有一个最重要的关系：

$$\begin{equation}\sin^2\theta+\cos^2\theta=1 \label{eq:edentity}\end{equation}$$

矢量

矢量，也称向量，是空间中同时具有大小和方向的对象。比如位移就是一个矢量。如果知道一个物体从某个特殊的点开始运动，知道物体运动多远还不能确定物体的运动终点，还需要知道位移的方向才行。用带箭头的线段可以直观地表示矢量，如图12。

矢量的符号表示是字母上加箭头，比如位移的符号可表示为$\vec{r}$，矢量的大小可用绝对值符号表示，比如位移的大小可表示为$|\vec{r}|$。

下面介绍矢量的相关运算。

可以用通常的实数乘以矢量。在矢量运算里，这种实数有个专门的名字，标量。用正数乘以矢量，会使矢量的大小增大为相应的倍数。用负数乘以矢量，使矢量的方向反向。比如$-2\vec{r}$，这个矢量的大小是矢量$\vec{r}$的大小的2倍，但方向相反。

矢量也可以相加。向量$\vec{A}$和$\vec{B}$相加，保持矢量方向不变，将它们平移，把它们如图13那样摆在一起，构成四边形，和矢量就是对角线。

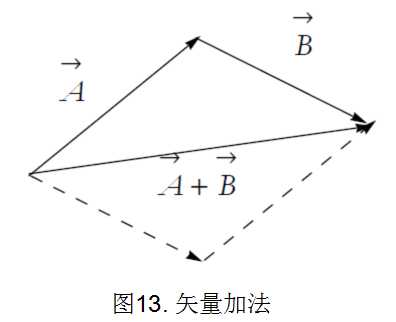
矢量也可以做减法。把一个矢量乘上-1，新矢量与另外一个矢量相加，所得矢量就是原来两个矢量的差矢量。

练习2：思考并写出矢量的减法法则。

矢量可以写成分量形式。先有三个坐标轴$x$, $y$, $z$，再定义三个单位矢量，方向分别沿坐标轴的方向，长度为1，这样的单位矢量也称基矢量。笛卡尔坐标系的三个基矢量传统上记为$\hat{i}$, $\hat{j}$, $\hat{k}$，如图14。如果三个坐标记为$(x_1,x_2,x_3)$，相应三个基矢量记为$\hat{e}_1$, $\hat{e}_2$, $\hat{e}_3$。

$V_x$, $V_y$, $V_z$为把三个基矢量加起来得到矢量$\vec{V}$所需要的数值系数，它们也称为矢量$\vec{V}$的分量。用基矢量就可以把一个任意矢量$\vec{V}$写成如下形式：

$$\begin{equation} \vec{V}=V_x\hat{i}+V_y\hat{j}+V_z\hat{k} \label{eq:lc} \end{equation}$$

方程$\ref{eq:lc}$也称为基矢量的线性组合。矢量分量可正可负。矢量也可以用分量写成这样的形式$(V_x, V_y, V_z)$。矢量的大小可由三维勾股定理求出，

$$\begin{equation} |\vec{V}|=\sqrt{V_x^2+V_y^2+V_z^2} \label{eq:norm} \end{equation}$$

标量$\alpha$与矢量$\vec{V}$可写成如下分量形式

$$\alpha\vec{V}=(\alpha V_x,\alpha V_y,\alpha V_z)$$

和矢量的三个分量分别为两个分量对应的分量的和，

$$\left (\vec{A}+\vec{B}\right )_x=A_x+B_x$$ $$\left (\vec{A}+\vec{B}\right )_y=A_y+B_y$$ $$\left (\vec{A}+\vec{B}\right )_z=A_z+B_z$$

矢量可以相乘吗？可以，但不止一种乘法。一种叫叉乘，我们这里先不讲。另一种叫点乘。我们下面说说点乘。两个矢量的点乘的结果是一个数，也即标量。两个矢量$\vec{A}$和$\vec{B}$的点乘的定义为

$$\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos\theta$$
其中，$\theta$为两个矢量的夹角。

点乘的分量形式为

$$\vec{A}\cdot\vec{B}=A_xB_x+A_yB_y+A_zB_z$$

练习3：证明一个矢量的大小满足$|\vec{A}|^2=\vec{A}\cdot\vec{A}$

练习4：两个矢量$\left(A_x=2, A_y=-3, A_z=1\right)$和$\left(B_x=-4, B_y=-3, B_z=2\right)$，计算这两个矢量的大小、点积及两个矢量的夹角

如果两个矢量的点积为0，称两个矢量正交，即互相垂直。

练习5：以下4个矢量，(1, 1, 1) (2, -1, 3) (3, 1, 0) (-3, 0, 2 )，找出正交的矢量对

练习6：你能解释两个正交的矢量的点积为什么为0吗？