插播数学3：偏微分

物理理论最低基础 Blog

---

“看那边，莱尼，那边的山和山谷美吗？”
“美，乔治。等我们有钱了我们能去那里吗？可以吗？”
乔治眯起眼睛：“你说的地方具体是哪里啊，莱尼？”
莱尼用手一指：“就是那里，乔治，那个小山谷。”

偏导数

多变量函数微积分是单变量函数微积分的推广。考虑一个多变量函数$V(x,y,z)$，自变量为$x$、$y$、$z$，这里它们不一定代表是坐标。另外，自变量数目可以多于或少于3个。

多变量微分的核心概念是偏导数。我们考虑一点$(x,y,z)$的邻域，固定$y$和$z$，看看$V$随$x$的变化率。我们想象$y$和$z$不变，那函数相当于只剩一个变量$x$了，那么$V$的导数就是

$$\begin{equation}\frac{dV}{dx}=\lim_{\Delta x \rightarrow 0}\frac{\Delta V}{\Delta x}\label{eq:der}\end{equation}$$

其中$\Delta V$定义为

$$\begin{equation}\Delta V=V(x+\Delta x,y,z)-V(x,y,z)\label{eq:dV}\end{equation}$$

注意到，$\Delta V$定义中，只有$x$有变化，$y$和$z$都没有变化。

方程($\ref{eq:der}$)和($\ref{eq:dV}$)定义的导数称为$V$对$x$的偏导数，记为

$$\frac{\partial V}{\partial x}$$
如果我们想强调$y$和$z$不变，也可记为
$$\left(\frac{\partial V}{\partial x}\right)_{y,z}$$

同样地，我们可以定义函数对另外任何一个变量的偏导数，如对$y$的偏导数为：

$$\frac{\partial V}{\partial y}=\lim_{\Delta y \rightarrow 0}\frac{\Delta V}{\Delta y}$$
$V$对$y$的偏导也可记为如下简化符号：
$$\frac{\partial V}{\partial y}=\partial_y V$$

多级导数也可定义。把$\frac{\partial V}{\partial x}$看成$x$、$y$、$z$的函数，也可以对其求微分。函数$V$对$x$二阶偏导为：

$$\frac{\partial^2 V}{\partial x^2}=\partial_x\left(\frac{\partial V}{\partial x}\right)=\partial_{x,x}V$$

还可定义混合偏导。比如，$\partial_y V$对$x$的偏导为

$$\frac{\partial^2 V}{\partial x \partial y}=\partial_x\left(\frac{\partial V}{\partial y}\right)=\partial_{x,y}V$$

混合偏导一个有趣并且很重要的性质是混合偏导与求导顺序无关，即

$$\frac{\partial^2 V}{\partial x \partial y}=\frac{\partial^2 V}{\partial y \partial x}$$

|练习1：求以下二元函数的一阶和二阶偏导（包括混合偏导）：$F(x,y)=x^2+y^2$、$F(x,y)=\sin(xy)$、$F(x,y)=\frac{x}{y}e^{(x^2+y^2)}$、$F(x,y)=e^x\cos y$|
|-----------|
（注：原文函数有误：$x^2+y^2=\sin(xy)$、$\frac{x}{y}e^{x^2+y^2}$）

驻点和函数极值

考虑一个一元函数$F(y)$，如图1所示。

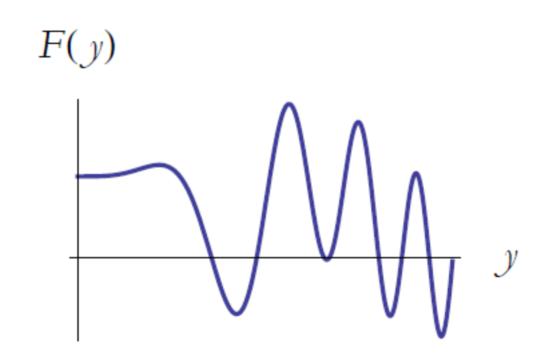
图1. 函数F(y)的图

在曲线上一些地方，$y$往任何方向变化，都会使函数值$F$增大，这些地方称为极小值点，见图2中的标记，

图2. 极小值点

在每个局域极小点往$y$的任何方向走，你都会高于点$F(y)$。每个点都处在一处洼地的底部。曲线上最低的极小值点称为最小值点。

函数在某点取极小值的一个条件是函数在此点对独立变量的导数为0。这是个必要条件，但不是充分条件。满足这一条件的点为驻点：

$$\frac{dF(y)}{dy}=0$$

要判断是不是极小值点还需要看看驻点的性质，也即对函数求二阶导数。如果二阶导数大于0，

$$\frac{d^2F(y)}{dy^2}>0$$
那么附近各点都高于驻点，此驻点为函数的极小值点。

如果函数在驻点的二阶导数小于0，

$$\frac{d^2F(y)}{dy^2}<0$$
那么附近各点都低于驻点，此驻点为函数的极大值点。见图3中标注各点。

图3. 极大值点

如果函数在驻点的二阶导数等于0，

$$\frac{d^2F(y)}{dy^2}=0$$
函数的导数在驻点改变符号，此驻点称为函数的拐点。

图4为拐点示例。

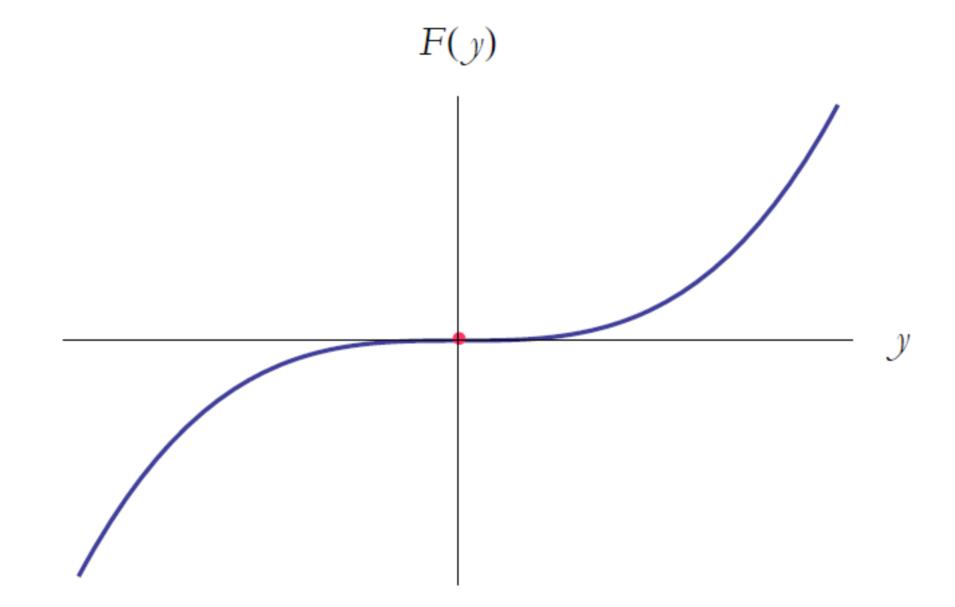
图4. 拐点

高维驻点

多变量函数也有极小值点、极大值点和驻点。想象一片山地，海拔高度是纬度和经度的函数，把函数记为$A(x,y)$，山峰和山谷分别为极大值点和极小值点。这些点还不是山区仅有的局部平坦的地方，还有两山之间的鞍点。见图5所示。

图5. 多变量函数

在山峰处，你不管往哪个方向走，你都会往低处走。在山谷处正相反，你不管往哪个方向走，你都会往高处走。但是这些地方都是平的。

还有些地方是平的。两山之间有些地方称为山鞍，鞍点也是平的。在鞍点你沿某个轴的任意方向，你的高度会上升，但是如果你沿垂直轴的任意方向走，你的高度又下降。

沿着$x$轴把山切开，并使刀片通过$A$的一个极小值点，见图6所示。

图6. 沿x轴切割函数

很明显，在极小值点$A$对$x$的导数为0，即

$$\frac{\partial A}{\partial x}=0$$

同样地，我们也可以沿$y$轴把山切开，于是也有

$$\frac{\partial A}{\partial y}=0$$

即在极小值点，或在驻点，函数对每个变量的一阶导数都为0。如果$A$的方向空间多于两个，在驻点$A$对所有方向$x_i$的导数都为0：

$$\begin{equation}\frac{\partial A}{\partial x_i}=0 \label{eq:Mstat}\end{equation}$$

以上方程有个简记法。当一点$x$变化一点点，函数值的改变量为

$$\delta A=\sum_i\frac{\partial A}{\partial x_i}\delta x_i$$

方程($\ref{eq:Mstat}$)等价于

$$\begin{equation}\delta A=0 \label{eq:Mstateq}\end{equation}$$

假设我们已经找到满足以上条件的一点，我们如何知道这一点是对应极小值点还是极大值点，抑或鞍点？我们需要看二阶导数。但是二阶导数有很多。比如对于二维的情况，我们有以下二阶导数：$\frac{\partial^2 A}{\partial x^2}$、$\frac{\partial^2 A}{\partial y^2}$、$\frac{\partial^2 A}{\partial x \partial y}$、$\frac{\partial^2 A}{\partial y \partial x}$，最后两个结果相等。

这些二阶导数写在一起，组成一个矩阵，这个矩阵叫做海森矩阵：

$$H=\begin{pmatrix}\frac{\partial^2 A}{\partial x^2}&\frac{\partial^2 A}{\partial x \partial y}\\\frac{\partial^2 A}{\partial y^2}&\frac{\partial^2 A}{\partial y \partial x}\\ \end{pmatrix}$$

关于矩阵的重要的量是行列式和迹。海森矩阵的行列式为

$$\mathrm{Det} H=\frac{\partial^2 A}{\partial x^2} \frac{\partial^2 A}{\partial y^2}-\frac{\partial^2 A}{\partial x \partial y} \frac{\partial^2 A}{\partial y \partial x}$$
迹为
$$\mathrm{Tr} H=\frac{\partial^2 A}{\partial x^2}+ \frac{\partial^2 A}{\partial y^2}$$

这里不具体解释矩阵、行列式和迹这些概念。你知道有这些东西还有以下规则就可以了：
如果海森矩阵的行列式和迹都是正的，那么对应的驻点为极小值点。
如果海森矩阵的行列式是正的，迹都是负的，那么对应的驻点为极大值点。
如果海森矩阵的行列式是正的，不管迹符号为何，对应的驻点为鞍点。

这里只写出了两变量函数的具体规则。对于更多变量的函数，规则的形式更为复杂。下面我们具体算一下两变量函数。比如，考虑函数

$$F(x,y)=\sin x + \sin y$$
求导，
$$\frac{\partial F}{\partial x}=\cos x$$
$$\frac{\partial F}{\partial y}=\cos y$$
由于$\cos\frac{\pi}{2}=0$，显然点$(\pi/2,\pi/2)$是一个驻点。

要知道这个点的类型，还得计算二阶导数

$$\frac{\partial^2 F}{\partial x^2}=-\sin x$$
$$\frac{\partial^2 F}{\partial y^2}=-\sin y$$
$$\frac{\partial^2 F}{\partial x \partial y}=\frac{\partial^2 F}{\partial y \partial x}=0$$

由于$\sin\frac{\pi}{2}=1$，计算海森矩阵的行列式和迹，行列式和迹都大于0，所以点$(\pi/2,\pi/2)$是个极小值点。

练习2：考虑以下各点$(\pi/2,-\pi/2)$、$(-\pi/2,\pi/2)$、$(-\pi/2,-\pi/2)$，判断这些点是不是以下函数$F(x,y)=\sin x +\sin y$、$F(x,y)=\cos x$的驻点，并判断驻点的类型。