第2讲：运动

Blog 物理理论最低基础

---

莱尼抱怨：“乔治，跳跃频闪的东西令我不爽。时间是蹦蹦跳跳而溜去的吗？我希望事情平滑而行。”乔治思考片刻，擦掉黑板，“好的，莱尼，今天我们就学习平滑变化的系统。”

插播数学：微分

在本书中，我们主要处理的问题是，看物理量如何随时间变化。经典力学主要研究事物如何平滑变化，用数学中的术语就是连续变化。状态将动力学定律随时间演化连续更新，不同于上一节中的频闪变化。因此，我们有兴趣学学独立变量$t$的函数。

数学上处理连续变化需要用微分。微分与极限密切相关，我们先讨论下极限。我们考虑一个数列$l_1$, $l_2$, $l_3$, $\ldots$, 它们越来越靠近某个值$L$，$L$即成为数列的极限。比如数列：0.9, 0.99, 0.999, 0.9999, . . . ，这个数列的极限为1。数列里没有数字1，但是它们越来越靠近1。我们用如下符号表示这个事情：

$$\lim_{i \rightarrow \infty }l_i=L$$
这个式子表示的意思是当$i$趋于无穷的时候，$L$为$l_i$的极限。

这个思想也可用于函数。我们考虑函数$f(t)$，我们想知道当$t$越来越靠近某个值（比如$a$）时函数值如何变化。如果当$t$趋近于$a$时，$f(t)$可任意接近某个值$L$，我们称$t$趋近于$a$时，$f(t)$的极限为$L$，记作

$$\lim_{_{t \rightarrow a} }f(t)=L$$

$f(t)$是变量$t$的函数，$t$变化，则$f(t)$也变化，微分就是讨论函数的变化率。想法是这样的，知道某瞬时的函数值为$f(t)$，然后让时间变化一点点，看看函数值变化多少。变化率为函数值$f$的变化量与自变量$t$变化量的比值。变化量用大写希腊字母$\Delta$表示，时间$t$的变化量即为$\Delta t$（注意这不是$\Delta \times t$）。在时间间隔$\Delta t$内，函数值从$f(t)$变化到$f(t+\Delta t)$，函数的变化量为

$$\Delta f=f(t+\Delta t)-f(t)$$

要精确定义时刻$t$时函数的变化量，必须让$\Delta t$趋于0，而此时，$\Delta f$也趋于0，但二者的比值一般不为0，有个极限值，这个极限就是$f(t)$对$t$的导数，

$$\begin{equation}\frac{df}{dt}=\lim_{\Delta t \rightarrow 0}\frac{\Delta f}{\Delta t} = \lim_{\Delta t \rightarrow 0}\frac{f(t+\Delta t)-f(t)}{\Delta t}\label{eq:derive}\end{equation}$$

现在让我们练习下求导计算。比如计算函数$f(t)=t^2$的导数。根据方程$\ref{eq:derive}$计算导数。先计算

$$f(t+\Delta t)=(t+\Delta t)^2=t^2+2t\Delta t+\Delta t^2$$
减去$f(t)$，
$$f(t+\Delta t)-f(t)=(t+\Delta t)^2-t^2=2t\Delta t+\Delta t^2$$
两边除去$\Delta t$，
$$\frac{f(t+\Delta t)-f(t)}{\Delta t}=\frac{2t\Delta t+\Delta t^2}{\Delta t}=2t+\Delta t$$
当$\Delta t$趋于0时，上式第一项不受影响，第二项将消失。记住一点：当计算导数时，$\Delta t$的高阶项将为0。因此，
$$\lim_{\Delta t \rightarrow 0}\frac{2t\Delta t+\Delta t^2}{\Delta t}=2t$$
即$t^2$的导数为
$$\frac{d(t^2)}{dt}=2t$$

下面我们考虑一般的幂函数，$f(t)=t^n$。先计算$f(t+\Delta t)=(t+\Delta t)^n$，它可由二项式定理进行计算，

$$\begin{equation*} \begin{split} f(t+\Delta t)=&(t+\Delta t)^n=t^n+nt^{n-1}\Delta t + \frac{n(n-1)}{2}t^{n-2}\Delta t^2\\ &+\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^3+\dots+\Delta t^n \end{split} \end{equation*}$$
减去$f(t)$，得
$$\begin{equation*} \begin{split} \Delta f=&f(t+\Delta t)-f(t)=t^n+nt^{n-1}\Delta t + \frac{n(n-1)}{2}t^{n-2}\Delta t^2\\ &+\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^3+\dots+\Delta t^n -t^n\\ =&nt^{n-1}\Delta t + \frac{n(n-1)}{2}t^{n-2}\Delta t^2\\ &+\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^3+\dots+\Delta t^n \end{split} \end{equation*}$$
除以$\Delta t$
$$\begin{equation*} \begin{split} \frac{\Delta f}{\Delta t}=&nt^{n-1} + \frac{n(n-1)}{2}t^{n-2}\Delta t\\ &+\frac{n(n-1)(n-2)}{3}t^{n-3}\Delta t^2+\dots+\Delta t^{n-1} \end{split} \end{equation*}$$
令$\Delta t \rightarrow 0$，得导数为
$$\frac{dt^n}{dt}=nt^{n-1}$$
即便$n$不是整数，上式依然成立，$n$可为任意实数或复数。

这里说几个特例。$n$=0$，此时$f(t)=1$，导数为0——任何常函数的导数也都为0。$n$=0$，此时$f(t)=t$，导数为1——变量 自己对自己的导数为1。

下面列举几个常见的导数。

$$\frac{d(\sin t)}{dt}=\cos t$$ $$\frac{d(\cos t)}{dt}=-\sin t$$ $$\begin{equation}\frac{d(e^t)}{dt}=e^t\label{eq:et}\end{equation}$$ $$\frac{d(\ln t)}{dt}=\frac{1}{t}$$

方程$\ref{eq:et}$值得说一说。如果$t$是整数，$e^t$的含义很明显，比如$e^3=e\times e \times e$。方程$\ref{eq:et}$就是$e^t$的定义，导数就是自身。

关于导数还有几条有用的规则。你可以作为联系证明一下。第一条规则，常数的导数为0。这容易理解，导数是变化率，而常数没有变化，因此有

$$\frac{dc}{dt}=0$$

常数与函数$f(t)$乘积也是函数，它的导数等于常数乘以函数$f(t)$的导数，

$$\frac{d(cf)}{dt}=c\frac{df}{dt}$$

函数代数和的导数等于各个函数导数的代数和，比如两个函数$f(t)$和和$g(t)$，有如下关系：

$$\frac{d(f+g)}{dt}=\frac{d(f)}{dt}+\frac{d(g)}{dt}$$
函数的积的导数满足如下关系：
$$\frac{d(fg)}{dt}=g(t)\frac{d(f)}{dt}+f(t)\frac{d(g)}{dt}$$

$f(g)$是$g$的函数，$g(t)$是$t$的函数，那么$f$最终是$t$的函数，这种函数称为隐函数。你要是想知道某个$t$对应的$f$值，你需要先计算$g(t)$，然后计算$f(g)$。函数$f$对时间$t$的导数满足如下关系：

$$\frac{d(f)}{dt}=\frac{d(f)}{dg}\frac{d(g)}{dt}$$
这称为链式规则。链式规则可以让你想出一个中间函数，方便地计算一个复杂的函数的导数。比如计算如下函数的导数，
$$f(t)=\ln t^3$$
设计一个中间函数$g(t)=t^3$，于是有$f(g)=\ln g$，然后应用链式规则
$$\frac{df}{dt}=\frac{df}{dg}\frac{dg}{dt}$$
应用求导公式，$\frac{df}{dg}=\frac{1}{g}$，$\frac{dg}{dt}=3t^2$，带入上式，
$$\frac{df}{dt}=\frac{3t^2}{g}$$
带入$g(t)=t^3$，得
$$\frac{df}{dt}=\frac{3}{t}$$

应用以上规则你可以方便地计算导数。以上基本上就是求导的所有规则。

练习1：计算以下函数的导数： $$f(t) = t^4 + 3 t^3 - 12 t^2 + t - 6$$ $$g(x)=\sin x - \cos x$$ $$\theta(\alpha)=e^{\alpha} + \alpha\ln \alpha$$ $$x(t)=\sin^2t-\cos t$$

（注：第4个函数原文误为$x(t)=\sin^2x-\cos x$）

练习2：导数的导数称为二阶导数，写为$\frac{d^2f(t)}{dt^2}$。计算练习1中各函数的二阶导数。

练习3：应用链式规则，计算以下函数的导数： $$g(t) = \sin(t^2) - \cos(t^2)$$ $$\theta(\alpha)=e^{3\alpha} +3\alpha\ln (3\alpha)$$ $$x(t)=\sin^2(t^2)-\cos(t^2)$$

练习4：证明函数和与积的求导法则和链式规则。

练习5：证明方程$\ref{eq:et}$。

粒子运动

点粒子是个理想化的概念，任何东西都如一个点那么小，即便是电子也不会那么小。但是，在很多情况下，我们可以忽略物体的形状，当做一个点来处理。比如地球显然不是一个点，但计算地球绕太阳公转时的轨道的时候，我们忽略地球的大小，也可以得到精度很高的结果。

粒子的位置可由三个空间坐标给出，粒子的运动通过每个时刻粒子的位置来定义。数学上，给出三个空间坐标随时间$t$变化的函数:$x(t)$，$y(t)$，$z(t)$，即指明了一个位置。

粒子在$t$时刻的位置还可以用矢量$\vec{r}(t)$表示，有三个分量$x(t)$，$y(t)$，$z(t)$。粒子走过的路径（称为轨迹）用$\vec{r}(t)$表示。经典力学要干的工作就是根据初始条件和动力学定律确定出$\vec{r}(t)$。

除了位置，粒子另外一个最重要的信息是速度。速度也是矢量。定义矢量需要一点微积分知识。

考虑一个粒子在$t$时刻及随后晚一点点时刻$t+\Delta t$的位移。在这个很小的时间间隔$\Delta t$内，粒子从$x(t)$，$y(t)$，$z(t)$处运动至$x(t+\Delta t)$，$y(t+\Delta t)$，$z(t+\Delta t)$，或者用矢量表示，从$\vec{r}(t)$运动至$\vec{r}(t+\Delta t)$处。位移可定义为：

$$\Delta x = x(t+\Delta t) - x(t)$$ $$\Delta y = y(t+\Delta t) - y(t)$$ $$\Delta z = z(t+\Delta t) - z(t)$$
或
$$\Delta \vec{r} = \vec{r}(t+\Delta t) - \vec{r}(t)$$
位移即是在粒子在很短的时间$\Delta t$内走过的位移。速度为位移除以时间$\Delta t$，并取极限$\Delta t$趋于零。如$x$方向的速度为
$$v_x = \lim_{\Delta t \rightarrow 0}\frac{\Delta x}{\Delta t}$$
这实际上就是$x$对时间求导。
$$v_x = \frac{dx}{dt}=\dot{x}$$ $$v_y = \frac{dy}{dt}=\dot{y}$$ $$v_z = \frac{dz}{dt}=\dot{z}$$

变量上一点表示对时间求导。这可以用于任何量对时间求导。比如$T$表示一壶水的温度，$\dot{T}$表示温度的时间变化率。这种表示方法我们还会多次遇到。

一直要写$x$，$y$，$z$，显得很繁琐，我们可约化成一个符号。坐标的三个分量可记为$x_i$，速度的分量可记为$v_i$：

$$v_i=\frac{dx_i}{dt}=\dot{x}_i$$
其中， $i$取的值为$x$，$y$，$z$。速度也可用矢量表示：
$$\vec{v}=\frac{d\vec{r}}{dt}=\dot{\vec{r}}$$
速度的大小为$|\vec{v}|$，
$$|\vec{v}|^2=v_x^2+v_y^2+v_z^2$$
速度的大小表示粒子运动的快慢，也称为速率。

加速度表示速度如何变化。粒子的速度如果是个常矢量，即粒子的速度不发生变化，则粒子没有加速度。速度是常矢量不仅仅表示速度的大小不发生变化，还表示速度的方向不发生变化。速度的大小和方向只要有其一发生变化，即速度发生变化，即有加速度。加速度是速度对时间的导数：

$$a_i=\frac{dv_i}{dt}=\dot{v}_i$$
用矢量表示：
$$\vec{a}=\frac{d\vec{v}}{dt}=\dot{\vec{v}}$$
$v_i$是$x_i$对时间的一阶导数，$a_i$是$v_i$对时间的一阶导数，因此，$a_i$是$x_i$对时间的二阶导数，
$$a_i=\frac{d^2x_i}{dt^2}=\ddot{v}_i$$
变量上面的两个点表示对时间的二阶导数。

举例

考虑一个粒子，自$t=0$时开始运动，运动方程如下：

$$x(t)=0$$ $$y(t)$$ $$z(t)=z(0)+v(0)t-\frac{1}{2}gt^2$$
很明显，粒子在$x$和$y$方向上没有运动，只沿着$z$轴运动，常数$z(0)$和$v(0)$表示$z$方向上粒子的初始位置和初始速度。$g$也是一个常数。

对时间求导，可得粒子的速度，

$$v_x(t)=0$$ $$v_y(t)=0$$ $$v_z(t)=v(0)-gt$$
速度的$x$和$y$分量总是零，速度的$z$分量在$t=0$时刻的值为$v(0)$。

随着时间的流逝，$-gt$这一项就不再是零了，最终会超过$v(0)$，粒子沿$z$轴负方向运动。

再对时间求一次导，可得粒子加速度，

$$a_x(t)=0$$ $$a_y(t)=0$$ $$a_z(t)=-g$$
加速度沿$z$轴方向，是个负的常数。如果$z$轴竖直向上，粒子向下加速，就像下落的物体那样。

下面我们考虑一个振荡的粒子，粒子在$x$方向往复运动。由于沿$y$和$z$方向没有运动，我们将其忽略。三角函数就可表示一个简单的振荡运动，

$$x(t)=\sin \omega t$$
其中，希腊字母$\omega$为常数，它的数值越大，表示振荡的越快，这种运动叫简谐振动，如图1所示。

下面计算速度和加速度。$x(t)$对时间的一阶导数即为速度，

$$v_x=\frac{dx(t)}{dt}=\frac{d}{dt}\sin \omega t = \omega \cos \omega t$$
加速度是$x(t)$对时间的二阶导数，也即$v_x(t)$对时间的一阶导数，
$$a_x=\frac{d^2x}{dt^2}=\frac{dv_x(t)}{dt}=-\omega^2\sin \omega t$$

有一些有趣的事情值得注意。当粒子处于最极大或最极小值时，粒子速度为零。fangu反过来，当粒子处于$x=0$处时，粒子速度达到极大或极小。这种情况我们称粒子位置与速度反相，相位差90°。见图2和图3。

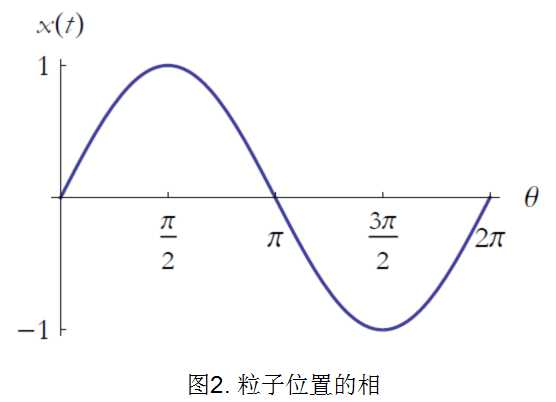
粒子位置与加速度也有联系，二者都正比于$\sin \omega t$，但是符号相反，当粒子位置是正(负)的时候，粒子的加速度为负(正)。即不管粒子在哪里，粒子都往原点加速，位置和加速度反相，相位差为180°。

练习6：粒子完成一个运动周期需要多长时间？

下一个例子，粒子绕原点做匀速圆周运动，即以恒定速率沿圆周运动。我们可以不考虑$z$轴，只考虑$x$, $y$平面上的运动。要描述这一运动，需要两个函数$x(t)$和$y(t)$。我们考虑粒子沿逆时针方向运动，轨迹的半径为$R$。

把运动投影到$x$和$y$轴上，可以使运动更直观。粒子绕着原点转圈，它的$x$坐标从$-R$到$R$之间来回变换，$y$坐标也是一样，但是$x$和$y$坐标有90°的相位差，当$x$坐标达到最大值，$y$坐标为0，反之亦然。

对于逆时针的匀速圆周运动，运动方程如下：

$$x(t)=R\cos \omega t$$ $$y(t)=R\sin \omega t$$
其中，$\omega$为圆频率，表示单位时间内粒子转过的角的弧度。粒子转一圈用的时间为运动周期：
$$T=\frac{2\pi}{\omega}$$

由运动方程就可以计算速度分量和加速度分量：

$$v_x=-R\sin \omega t$$ $$v_y=R\cos \omega t$$ $$a_x=-R^2\cos \omega t$$ $$a_y=-R^2\sin \omega t$$

可以看出圆周运动一个有趣的性质：加速度与位置矢量平行反向，即加速度的方向指向原点。牛顿曾用这个性质分析过月亮的运动。

练习7：证明位置矢量和速度矢量正交

练习8：给出以下位置矢量，计算对应的速度矢量和加速度矢量，并用画图软件作出各位置矢量及其对应的s速度矢量和加速度矢量的图。 $$\vec{r}=(\cos \omega t, e^{\omega t})$$ $$\vec{r}=\left (\cos (\omega t-\phi), \sin (\omega t-\phi)\right)$$ $$\vec{r}=(c\cos^3t,c\sin^3t)$$