计算物理期末作业（random walks）

王冠 天眷班 2014301020003

摘要

　　在以前我们学习过不确定的系统如混沌系统，但大多数时候我们将重点放在确定性的系统上，这次作业我们研究一个随机系统———随机行走。

背景

　　随机游走（random walk）也称随机漫步，随机行走等是指基于过去的表现，无法预测将来的发展步骤和方向。核心概念是指任何无规则行走者所带的守恒量都各自对应着一个扩散运输定律，接近于布朗运动，是布朗运动理想的数学状态，现阶段主要应用于互联网链接分析及金融股票市场中。　

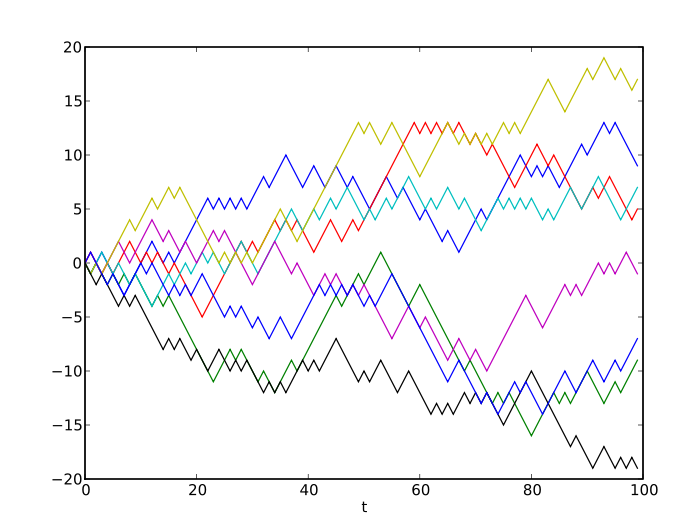
正文

　　首先我们要构建模型，和普通的动态系统不同，随机行走没有动态方程。但是他的运动可以按照如下过程来进行描述：
　　首先设置一个位置为ｘ，然后产生一个随机数ｍ（０＜＝ｍ＜＝１），将ｍ和一个确定的概率数Ｐ进行比较，当ｍ大于Ｐ时，ｘ＋１，当ｍ小于Ｐ时，ｘ－１。（此时假设每一步都是均匀的）
　　同时行走的距离$x^{2}$与时间t成正比。
　　则程序如下：

import numpy as np
from pylab import *
from math import *
import random
def Random_walk():
    x=[0]
    x2=[0]
    global n
    n=100
    for i in range(n):
        r=random.uniform(0,1)
        if r<0.5:
            x.append(x[i]+1)
        else:
            x.append(x[i]-1)
        x2.append(x[i+1]**2)
        print r
    x2=array(x2)
    return [x,x2]
n=100
time=range(n+1)
m=500
x_1=Random_walk()[0]
x_2=Random_walk()[0]
x2=Random_walk()[1]
for i in range(m):
    x2=x2+Random_walk()[1]
x2=x2/(m+1)
figure(figsize=[16,8])
subplot(121)
plot(time,x_1)
plot(time,x_2)
xlim(0,100)
xlabel('step number')
ylabel('x')
title('Random walk in one dimension')
subplot(122)
scatter(time,x2,s=1)
plot(time,time)
xlim(0,100)
xlabel('step number')
ylim(0,100)
ylabel('$<x^2>$')
title('Random walk in one dimension')
show()

运行结果如下：
1、


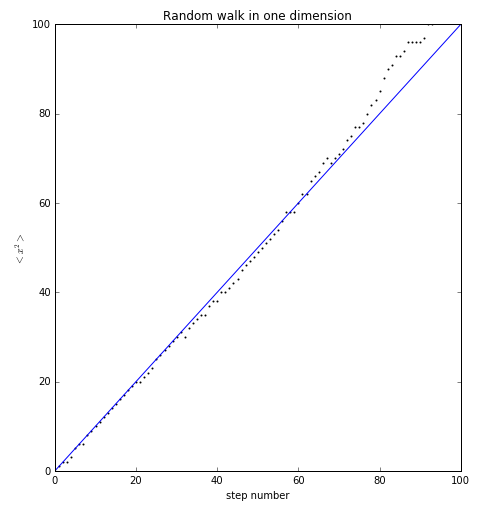
2、


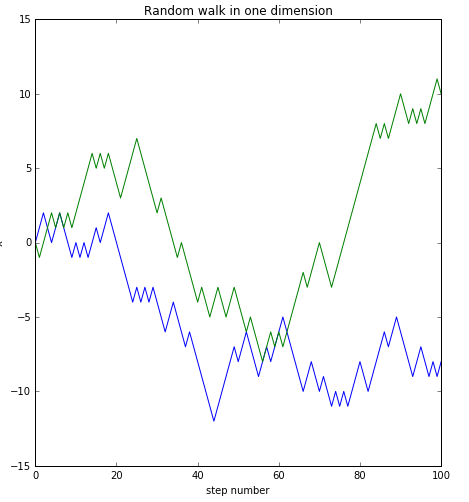
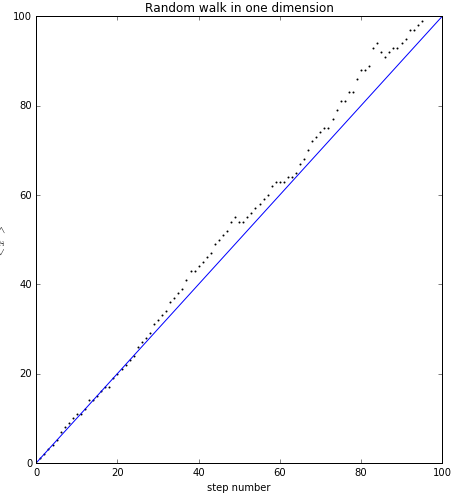
　　由两次运行结果可知，即使对于相同的程序，运行多次结果也是完全不同的，同时由运行结果图二可知，这些点都在一条线的附近，因此$x^{2}$与时间t呈线性关系。
此为一般情况下的随机行走情况，下面对随机行走进行多方面考虑：
（1）随机行走中向左走和向右走的概率不一样，假设向左走的概率P=0.3，则有

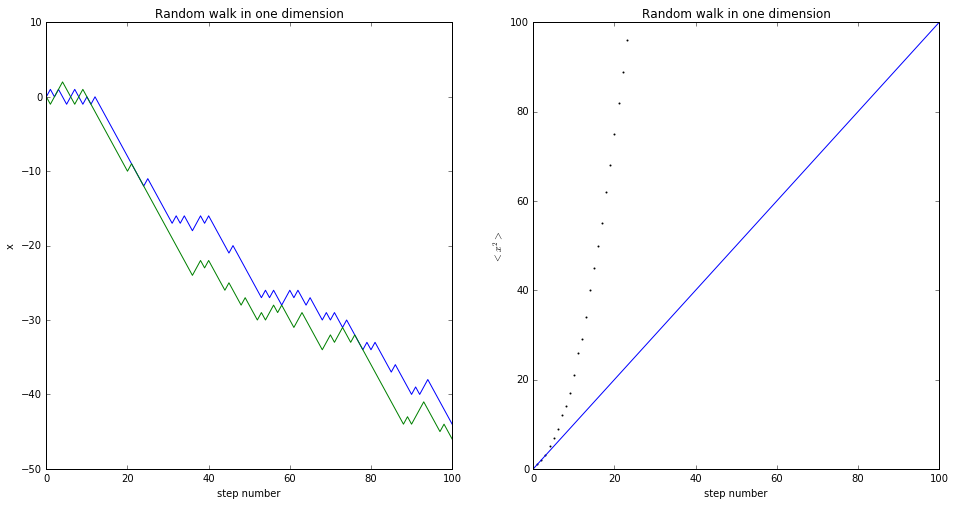
可以看出此时运行结果已经有蛮大的偏向性。
（2）随机行走中一步迈的距离随机，处于0~1之间，则程序为：

import numpy as np
from pylab import *
from math import *
import random
def Random_walk():
    x=[0]
    x2=[0]
    global n
    n=100
    for i in range(n):
        dx=random.uniform(-1,1)
        x.append(x[i]+dx)
        x2.append(x[i+1]**2)
    x2=array(x2)
    return [x,x2]
n=100
time=range(n+1)
m=500
x_1=Random_walk()[0]
x_2=Random_walk()[0]
x2=Random_walk()[1]
for i in range(m):
    x2=x2+Random_walk()[1]
x2=x2/(m+1)
time=array(time)
figure(figsize=[16,8])
subplot(121)
plot(time,x_1)
plot(time,x_2)
xlim(0,100)
xlabel('step number')
ylabel('x')
title('Random step length')
subplot(122)
scatter(time,x2,s=1)
plot(time,time/3.0)
xlim(0,100)
xlabel('step number')
ylim(0,)
ylabel('$<x^2>$')
text(60,15,'$<x^2>=t/3$')
title('Random step length')
show()

运行结果为：

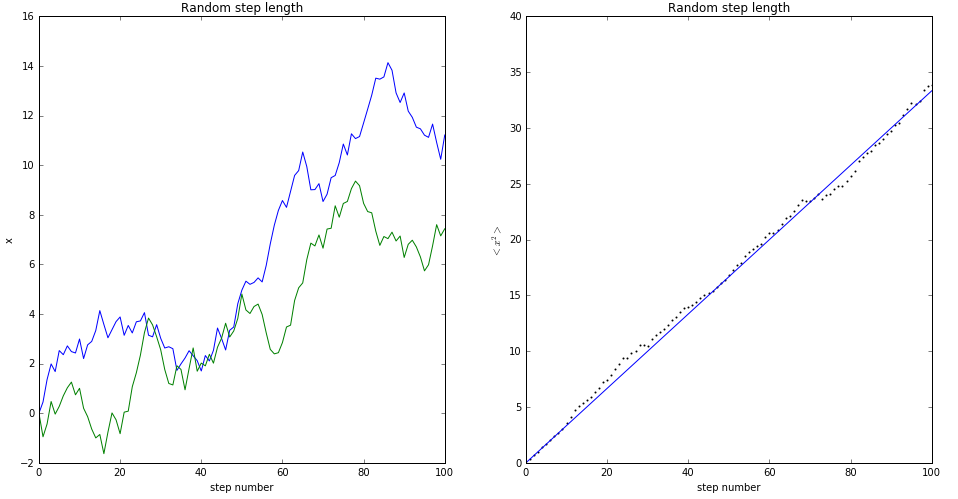
（3）二维运动时，在程序中用两个数组进行表示即可，可得到如下运行结果：

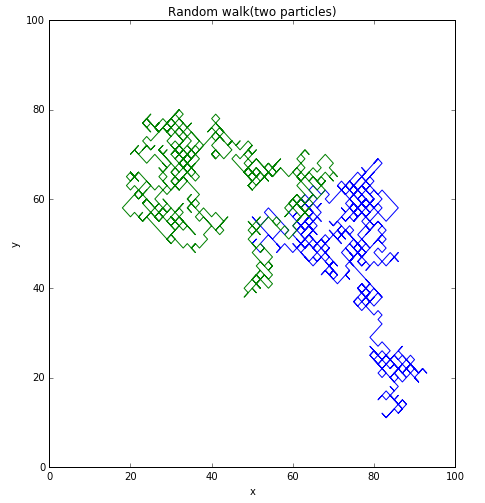
（4）在三维运动中，其运动程序如下：

import numpy as np
from pylab import *
from math import *
import random
import mpl_toolkits.mplot3d
def Random_walk():
    x=[0]
    y=[0]
    z=[0]
    r2=[0]
    global n
    n=500
    for i in range(n):
        r_x=random.uniform(0,1)
        r_y=random.uniform(0,1)
        r_z=random.uniform(0,1)
        if r_x<0.5:
            x.append(x[i]+1/sqrt(3))
        else:
            x.append(x[i]-1/sqrt(3))
        if r_y<0.5:
            y.append(y[i]+1/sqrt(3))
        else:
            y.append(y[i]-1/sqrt(3))
        if r_z<0.5:
            z.append(z[i]+1/sqrt(3))
        else:
            z.append(z[i]-1/sqrt(3))
        r2.append(x[i+1]**2+y[i+1]**2+z[i+1]**2)
    r2=array(r2)
    return [x,y,z,r2]
n=500
time=range(n+1)
m=500
Ran=Random_walk()
x=Ran[0]
y=Ran[1]
z=Ran[2]
r2=Ran[3]
for i in range(m):
    r2=r2+Random_walk()[3]
r2=r2/(m+1)
fig = figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x, y, z)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
title('random walk(three dimension)')
figure()
scatter(time,r2,s=1)
plot(time,time)
xlim(0,500)
xlabel('step number')
ylim(0,500)
ylabel('$<x^2>$')
title('Random walk(three dimension)')
show()

运行结果为：

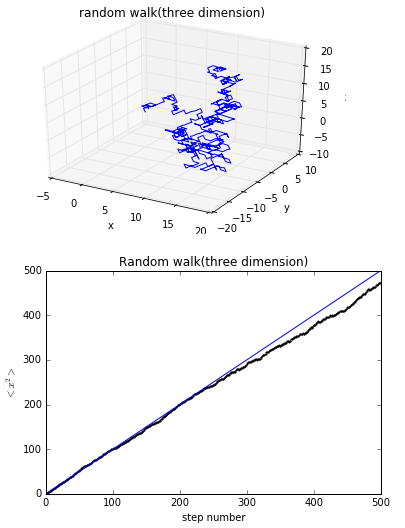
由图二可以看出，其运动距离与步数仍然成正比线性关系。
1000步时

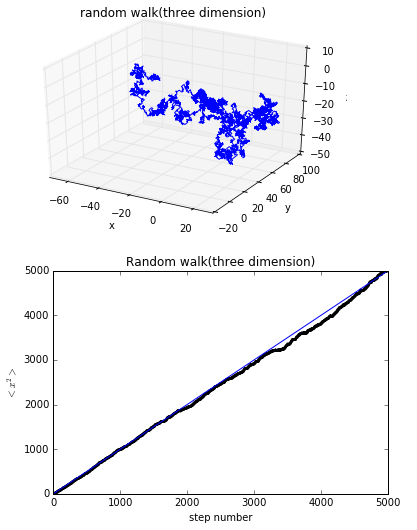
5000步时

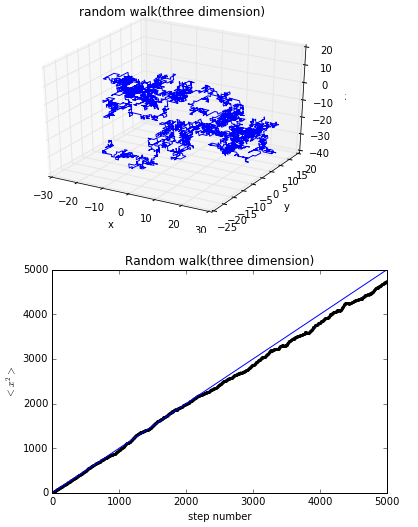
结论

随机行走模型在实际操作中具有很大的不确定性，但是距离与步数具有一定的关系（大多为线性）。

致谢及参考文献

蔡教授的认真指导.
宗玥同学的耐心讨论.
Nicholas J. Giordano & Hisao Nakanishi.计算物理.清华大学出版社.