@zy-0815
2016-11-26T16:35:08.000000Z
字数 3846
阅读 3091
计算物理第十次作业
计算物理
摘要
我们将研究行星的轨道运动,探究其影响因素,并应用于研究水星近日点进动,同时解答习题4.8和4.10
背景
太阳系,作为我们探索外太空的第一步,一直以来备受我们关注,而对他的探索也从未停止。为何唯独这看似普通的第三颗行星上会出现智慧生命,还有没有未被探测到的新行星,太阳系内还有那些适宜生命生存的地方。而了解这一切的起源,都基于我们对太阳系最初的探索,即行星轨道的观测和计算。
1. 基本运动公式
根据我们之前学过的知识,即牛顿定律,我们知道地球和太阳间的引力遵循如下公式:
其中和分别为太阳和地球的质量,为日地距离,为万有引力常数
因此我们有:
考虑到,则有:
又因为:,使用欧勒法则有:
2.开普勒三定律:
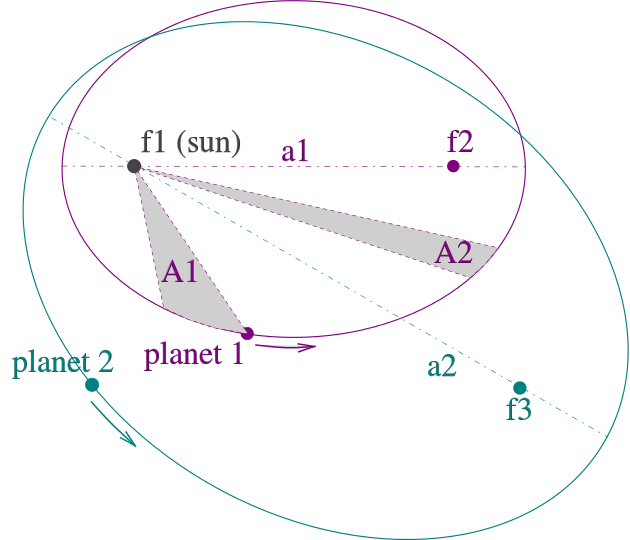
1.所有行星绕太阳的轨道都是椭圆,太阳在椭圆的一个焦点上。
2.行星和太阳的连线在相等的时间间隔内扫过相等的面积。
3.所有行星绕太阳一周的恒星时间(T )的平方与它们轨道长半轴(a)的比值是一个常数,即
3. 平方反比定律和轨道稳定性
极坐标下的运动方程:
考虑及我们可以解出:
其中为偏心率,当时为圆,时为椭圆,时为抛物线,时为双曲线。
我们研究行星运动,故只考虑椭圆,则有,, 且则有
我们不禁会考虑,若引力不是平方反比会怎样,因此对于
我们可以考虑改变的值来观察轨道的变化
3. 水星近日点进动
根据相对论,我们修正万有引力
正文
1. 主体程序
import pylab as plimport mathclass Solar_system :def __init__(self,i=0,initial_x=1,initial_y=0,initial_vx=0,initial_vy=2*math.pi,\total_time=10, time_step=0.002, radius=1):self.x=[initial_x]self.y=[initial_y]self.vx=[initial_vx]self.vy=[initial_vy]self.r=[radius]self.time=total_timeself.dt=time_stepself.t=[0]def run(self):_time=0while(_time<self.time):self.vx.append(self.vx[-1]-4*pow(math.pi,2)*self.x[-1]/pow(self.r[-1],3)*self.dt)self.x.append(self.x[-1]+self.vx[-1]*self.dt)self.vy.append(self.vy[-1]-4*pow(math.pi,2)*self.y[-1]/pow(self.r[-1],3)*self.dt)self.y.append(self.y[-1]+self.vy[-1]*self.dt)self.t.append(_time)_time += self.dtdef show_results(self):pl.plot(self.x,self.y)pl.title('Solar system')pl.xlabel('x(AU)')pl.ylabel('y(AU)')pl.legend()pl.show()a = Solar_system()a.run()a.show_results()
2. 平方反比定律和轨道稳定性
我们为了研究非平方反比定律下行星轨道,因此这里需要修改万有引力公式,即
因此在程序中需要修改
self.r.append(math.sqrt(pow(self.x[-1],2)+pow(self.y[-1],2)))self.vx.append(self.vx[-1]-4*pow(math.pi,2)*self.x[-1]/pow(self.r[-1],1+self.beta)*self.dt)self.x.append(self.x[-1]+self.vx[-1]*self.dt)self.vy.append(self.vy[-1]-4*pow(math.pi,2)*self.y[-1]/pow(self.r[-1],1+self.beta)*self.dt)self.y.append(self.y[-1]+self.vy[-1]*self.dt)
3.水星近日点进动
这里需要考虑相对论效应,修改万有引力公式:
故程序修改如下
self.r.append(math.sqrt(pow(self.x[-1],2)+pow(self.y[-1],2)))self.vx.append(self.vx[-1]-4*pow(math.pi,2)*(1+self.alpha/pow(self.r[-1],2))*self.x[-1]/pow(self.r[-1],1+self.beta)*self.dt)self.x.append(self.x[-1]+self.vx[-1]*self.dt)self.vy.append(self.vy[-1]-4*pow(math.pi,2)*(1+self.alpha/pow(self.r[-1],2))*self.y[-1]/pow(self.r[-1],1+self.beta)*self.dt)self.y.append(self.y[-1]+self.vy[-1]*self.dt)
结论
1.开普勒定律
基本图像(圆轨道)
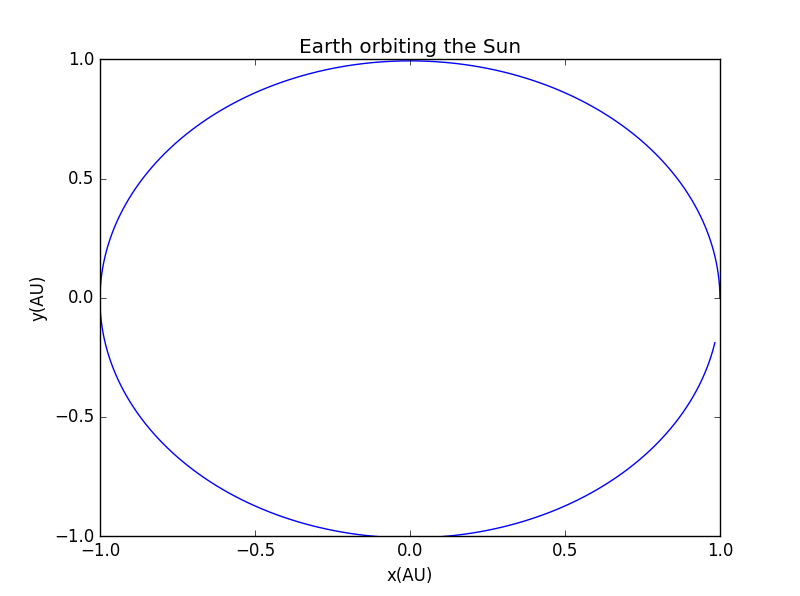
椭圆轨道
我们可以通过修改e的值来影响轨道形状:
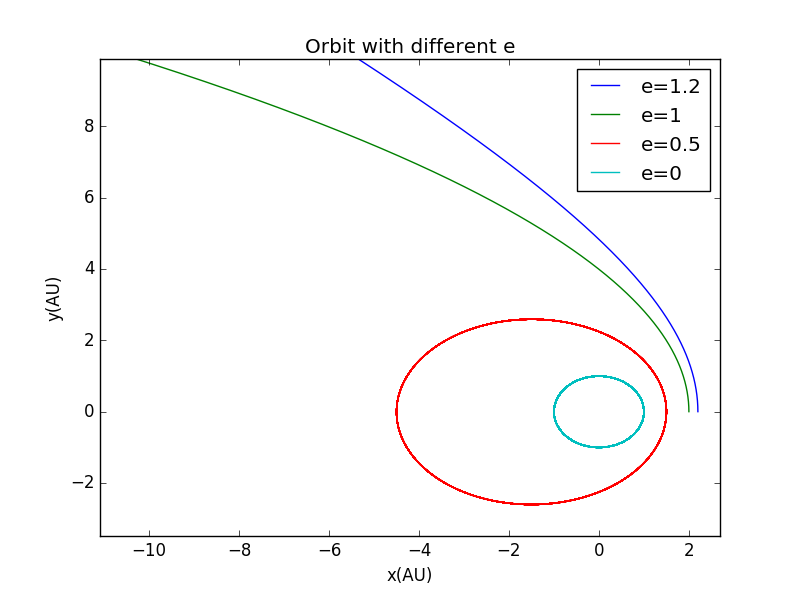
即当时为圆,时为椭圆,时为抛物线,时为双曲线。
当然,我们也可以通过改变初始速度达到目的:
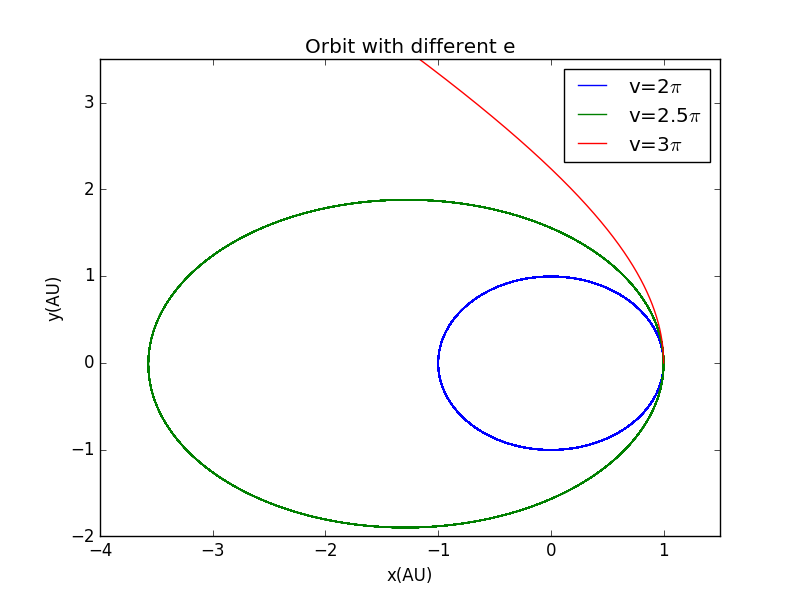
这也是航天器变轨的基本规律
2.平方反比定律
若我们将的指数改变,会引起一系列变化
为了对比方便,我们将坐标轴范设为相同,且打点画图:
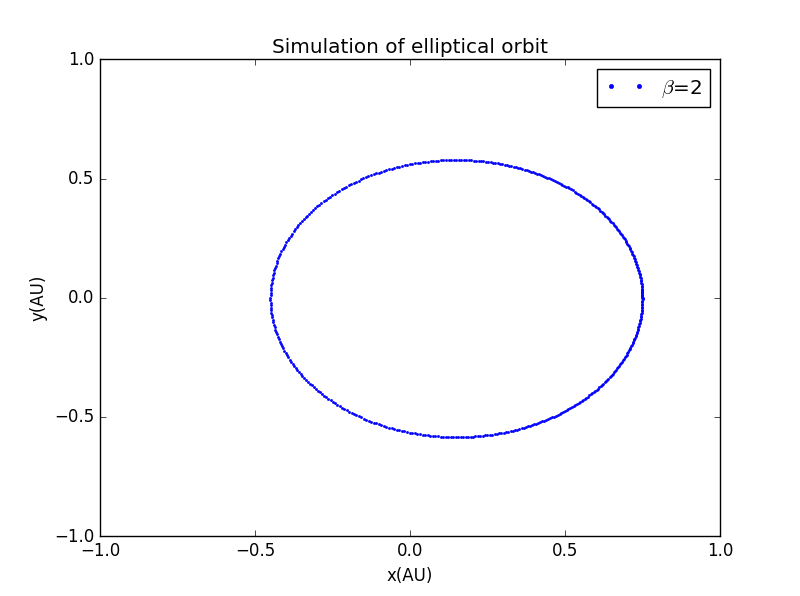
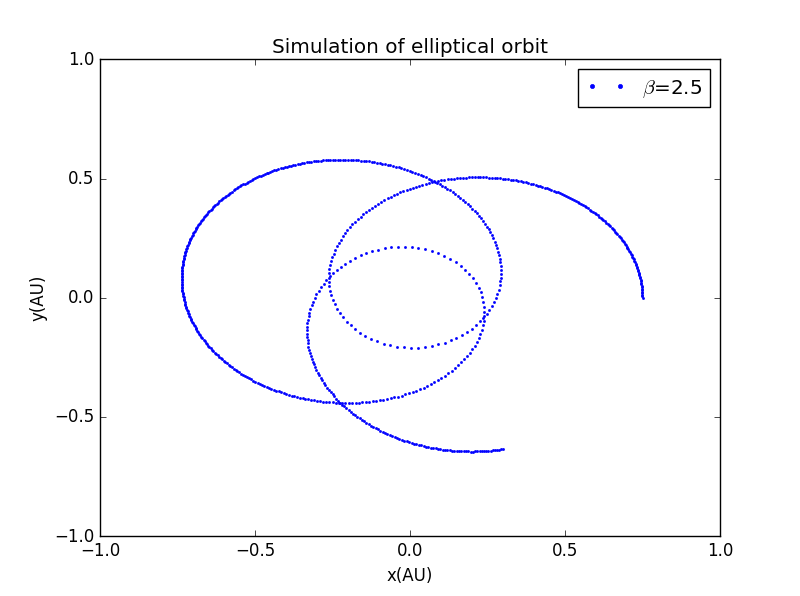
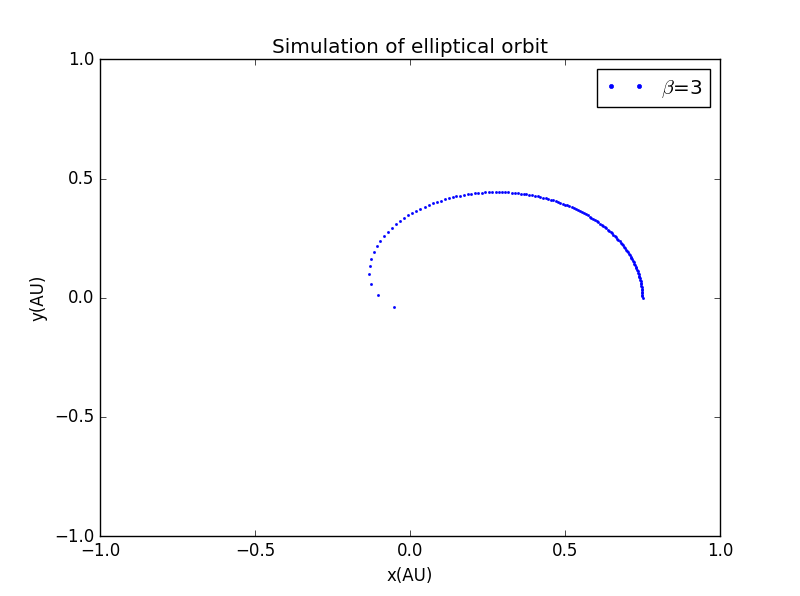
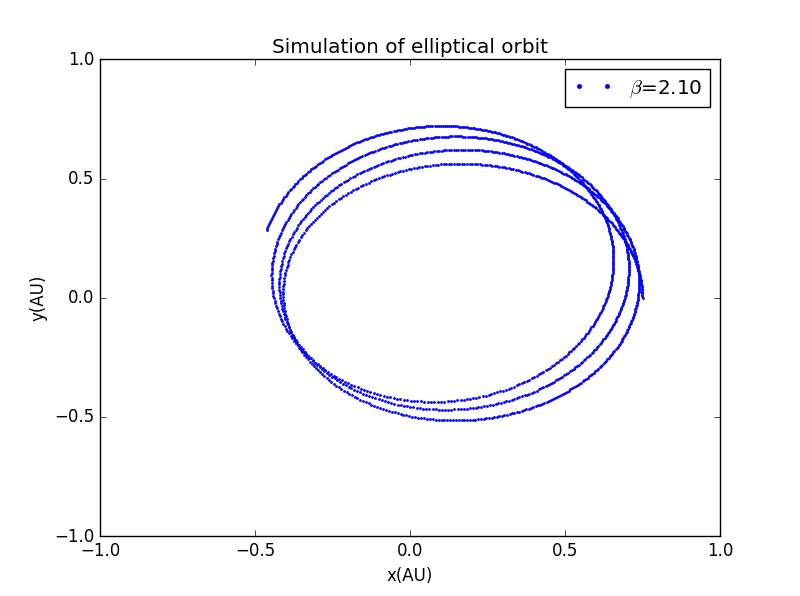
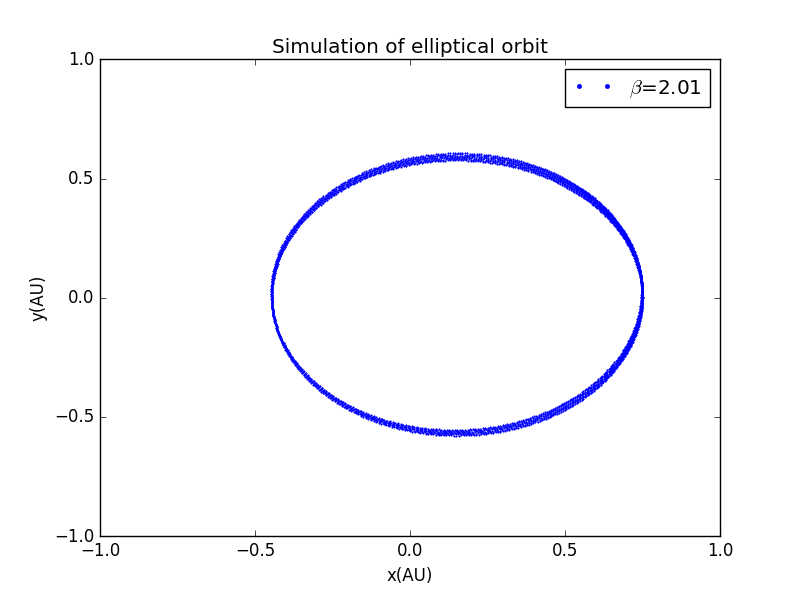
3.近日点进动
这里我们考虑实际的参量,即,,,,因此我们调整坐标系及参量绘图如下
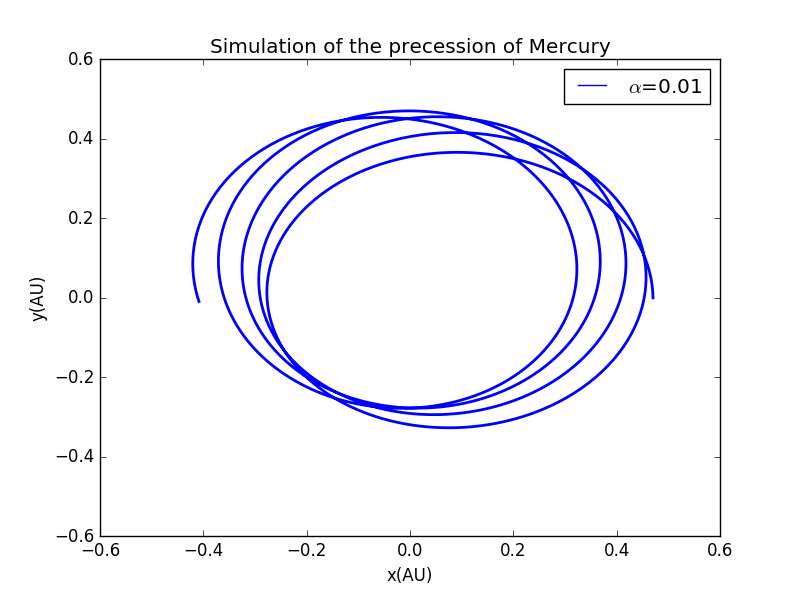
分析和的关系:
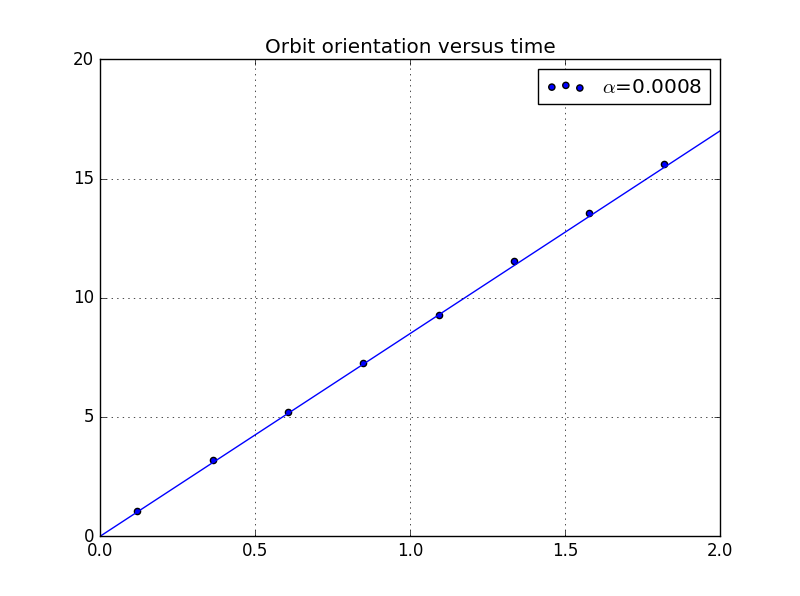
我们可以改变的值,从而得到不同的结果:
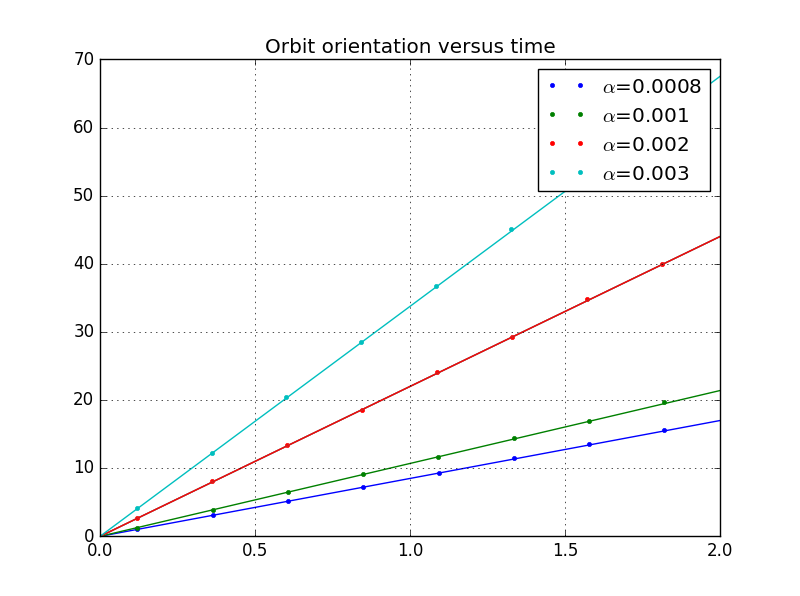
因此我们还可以做出和的图像如下:
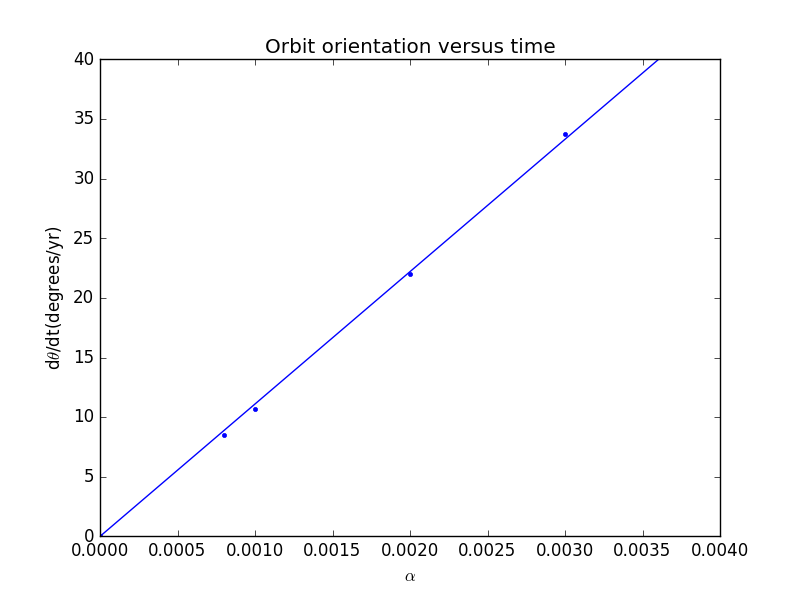
4.Vpython
当然,我们还可以用Vpython对运动进行模拟,以更好的了解行星的运动

致谢
张梓桐同学帮忙指正了一些小bug
