计算物理第七次作业

计算物理

---

摘要

本次作业就3.12 3.13 3.14题进行解答,即对单摆运动进行进一步的探讨，包括两个同时释放但初始角度有细微差别的单摆间角度的关系，以及角度和角速度之间的关系。

背景介绍

单摆作为物理学中一例经典的理想模型，我们在之前的学习中以及有了比较深刻的了解，这里我们通过计算机，将通过对其运动图像的分析和观察，从而对简谐振动有更进一步的理解和认识。

正文

1. 单摆和阻尼运动

首先，我们需要做基本的准备工作，即做出简谐摆的运动图像，为了尽可能考虑实际情况，我们还需要引入阻尼项和受迫振动项。

$$\begin{eqnarray*} \frac{d^2\theta}{dt^2}&=&-\frac{g}{l}\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)\\ if　we　set　\omega&=&\frac{d\theta}{dt}\\ \frac{d\omega}{dt}&=&-\frac{g}{l}\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)\\ \frac{d\theta}{dt}&=&\omega\\ So　we　have\\ \omega_{i+1}&=&\omega_i-(\frac{g}{l}\theta+q\frac{d\theta}{dt}-F_Dsin(\Omega_Dt))dt　　　　(1)\\ \theta_{i+1}&=&\theta_i+\omega_{i+1}dt　　　　　　　　　　　　　　　　　(2)\\ \end{eqnarray*}$$
由上面（1）（2）式，我们可以写出如下程序：

import pylab as pl
import math
class Simple_Pendulum :
    def __init__(self,i=0,initial_theta=0.2,time_step=0.04,total_time=20,length=1,\
                 g=9.8, initial_omega=0,q=1,Fd=0.2,omegaD=2):
        self.theta=[initial_theta]
        self.theta0=[initial_theta]
        self.t=[0]
        self.omega=[initial_omega]
        self.dt=time_step
        self.time=total_time
        self.g=g 
        self.l=length
        self.q=q
        self.Fd=Fd
        self.omegaD=omegaD
    def run(self):
        _time=0
        while(_time<self.time):
            self.omega.append(self.omega[-1]-((self.g/self.l)*math.sin(self.theta[-1])+\
                 self.q*self.omega[-1]-self.Fd*math.sin(self.omegaD*self.t[-1]))*self.dt)            
            self.theta.append(self.theta[-1]+self.omega[-1]*self.dt)
            self.t.append(_time)            
            _time += self.dt
    def show_results(self):
        pl.plot(self.t,self.theta)
        pl.xlabel('time(s)')
        pl.ylabel('theta')
        pl.show()
a = Simple_Pendulum()
a.run()
a.show_results()  

程序运行结果如图：

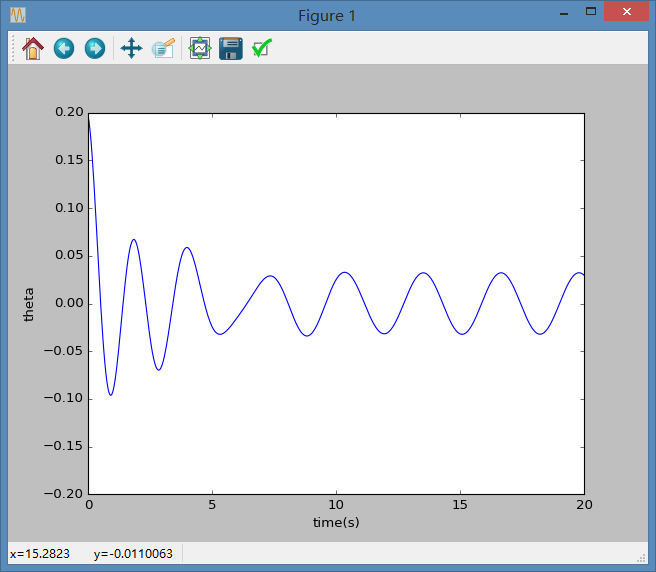
结果与书上Figure 3.5相同

2. Problem 3.13&3.14

接下来开始考虑两单摆角度差的关系，并回答习题3.13和3.14相关内容

2.1 首先，我们先进行准备工作，即作出$\Delta \theta$与t的关系图像，这里仅需将代码做如下改动：

self.omega1.append(self.omega1[-1]-((self.g/self.l)*math.sin(self.theta1[-1])+\
self.q*self.omega1[-1]-self.Fd*math.sin(self.omegaD*self.t[-1]))*self.dt)            
self.theta1.append(self.theta1[-1]+self.omega1[-1]*self.dt)
self.omega2.append(self.omega2[-1]-((self.g/self.l)*math.sin(self.theta2[-1])+ self.q*self.omega2[-1]-self.Fd*math.sin(self.omegaD*self.t[-1]))*self.dt)            
self.theta2.append(self.theta2[-1]+self.omega2[-1]*self.dt)

另外为了更加直观地看出变化，还需将坐标轴纵轴改为对数坐标，这一功能通过函数semilog实现，结果如图：

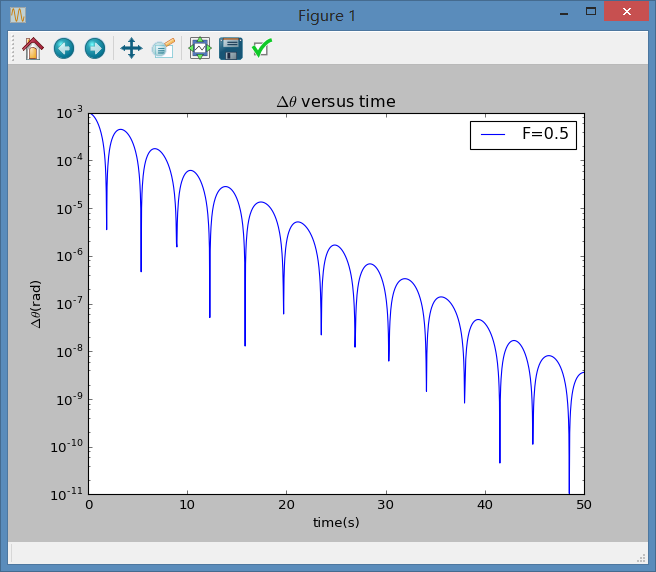
2.2 我们考虑给予两个摆不同的阻尼系数，首先，我们先看不同阻尼系数下的运动情况：

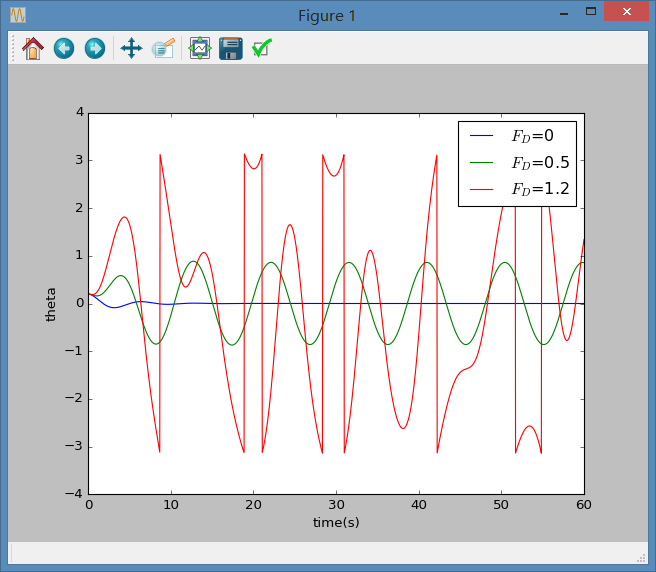
为了效果更明显，我们选择0.5与1.2两个，修改程序后，我们得到如下结果：

这里我们取$F_{D1}=0.5,F_{D2}=1.2$

3. Problem 3.12

3.1 首先我们作出最基本的图像，即用点图作出$\theta与\omega$的关系图像，主程序如下：

import pylab as pl
import math
class Simple_Pendulum :
    def __init__(self,i=0,initial_theta=0.2,time_step=0.04,total_time=60,length=9.8,\
                 g=9.8, initial_omega=0,q=0.5,Fd=0.5,omegaD=0.66667):
        self.theta=[initial_theta]
        self.theta0=[initial_theta]
        self.t=[0]
        self.omega=[initial_omega]
        self.dt=time_step
        self.time=total_time
        self.g=g 
        self.l=length
        self.q=q
        self.Fd=Fd
        self.omegaD=omegaD
    def run(self):
        _time=0
        while(_time<self.time):
            self.omega.append(self.omega[-1]-((self.g/self.l)*math.sin(self.theta[-1])+\
                 self.q*self.omega[-1]-self.Fd*math.sin(self.omegaD*self.t[-1]))*self.dt)            
            self.theta.append(self.theta[-1]+self.omega[-1]*self.dt)
            self.t.append(_time)            
            _time += self.dt
            if(self.theta[-1]>=math.pi):
                self.theta[-1]=self.theta[-1]-2*math.pi
            if(self.theta[-1]<=-math.pi):
                self.theta[-1]=self.theta[-1]+2*math.pi 
    def show_results(self):
        pl.plot(self.theta,self.omega,'.')
        pl.xlabel('time(s)')
        pl.ylabel('theta')
        pl.legend()
        pl.ylim(-1,1)
        pl.show()        
        pl.title('$\omega$ versus $\\theta$ with $F_{D}$=0.5' )
a = Simple_Pendulum()
a.run()
a.show_results()  

结果如图：

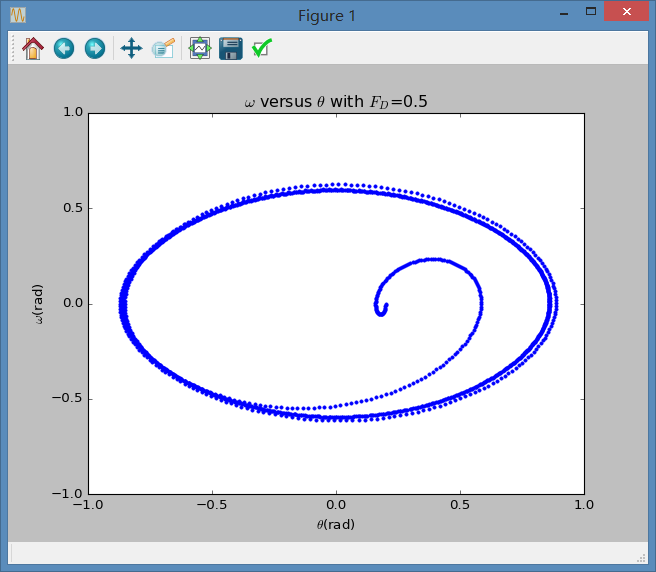
3.2 这时，我们改变打点的方式，即令只在满足$t=2\pi n/\Omega_D$时打点，其中n为整数，则我们需要修改程序如下，即添加筛选功能的部分。考虑到约等号，即t不会是$2\pi/\Omega$的整数倍，即余数不会完全等于0，故仅令其小于0.1（其实更小会更符合题目要求，但为使图像效果更好，此时的总时长已被修改为3000，更大精度意味着更长的计算时间，考虑到计算能力如此更合适）：

if(self.t[-1]%(2*math.pi/self.omegaD)<0.1):
    self.a.append(self.omega[-1])
    self.b.append(self.theta[-1])

这样，我们得到如下图像：

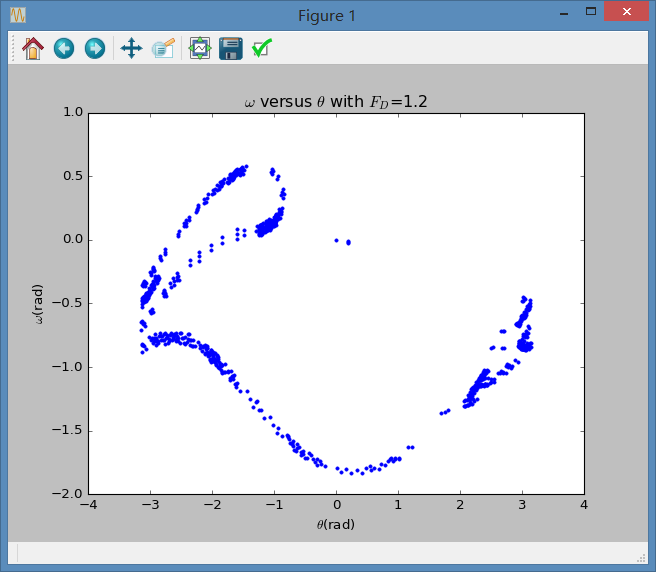
3.3 接下来，我们改变条件，即令 $t$ 满足最大驱动力或在相空间最高点差$\pi/4$时打点，则需将条件修改如下：

if((self.t[-1]-math.pi/4)%(2*math.pi/self.omegaD)<0.1 ):
     self.a.append(self.omega[-1])
     self.b.append(self.theta[-1])

结论

我们通过以上的探索，可以整理结果如下：
1. $\Delta \theta$与$t$的关系如下图所示：

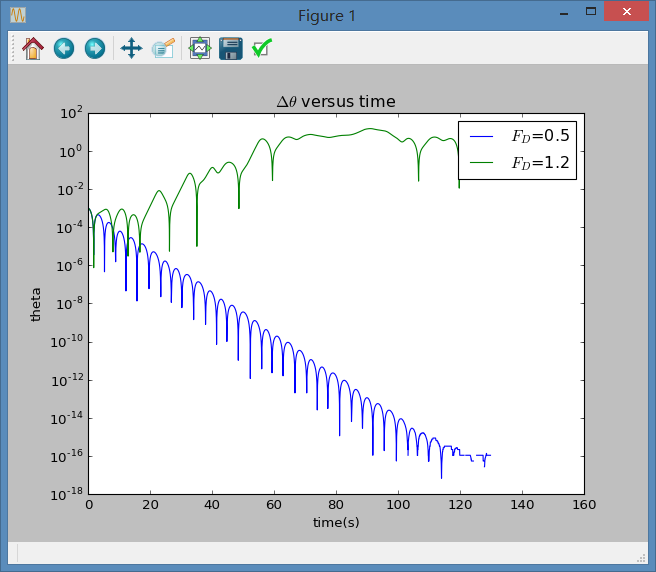
2.当我们使初始的两个单摆有不同的阻尼系数时，有如下图像：

3.随后考虑$\omega与\theta$之间的关系，此时仅当$t$满足$t=2\pi n/\Omega_D$时打点如下：

当$t$ 满足最大驱动力或在相空间最高点差$\pi/4$时打点时：

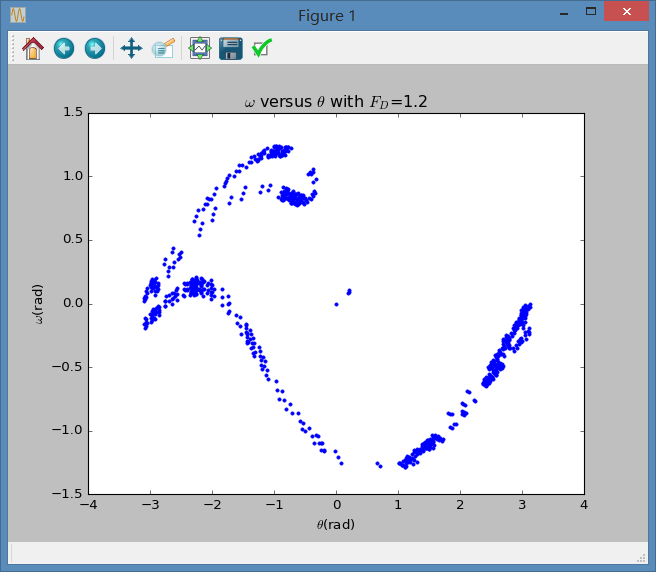
可见明显不同

反思：
1.正如figure 3.6下写道注意控制角度$\theta$的范围，否则会对结果造成影响，在本次作业初始阶段，写带受迫振动项的单摆运动程序时便出现了下列状况。开始由于没有考虑$\theta$的范围，所做图像如下：

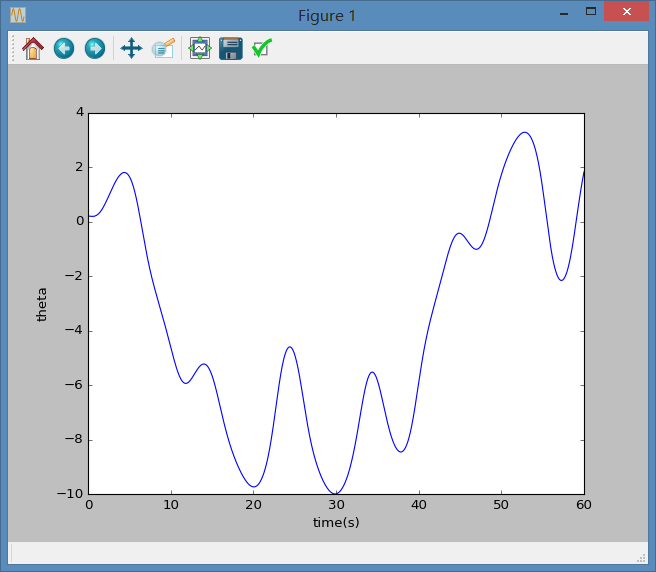
考虑后修正程序如下：

if(self.theta[-1]>=math.pi):
    self.theta[-1]=self.theta[-1]-2*math.pi
if(self.theta[-1]<=-math.pi):
    self.theta[-1]=self.theta[-1]+2*math.pi

所绘图像如下：

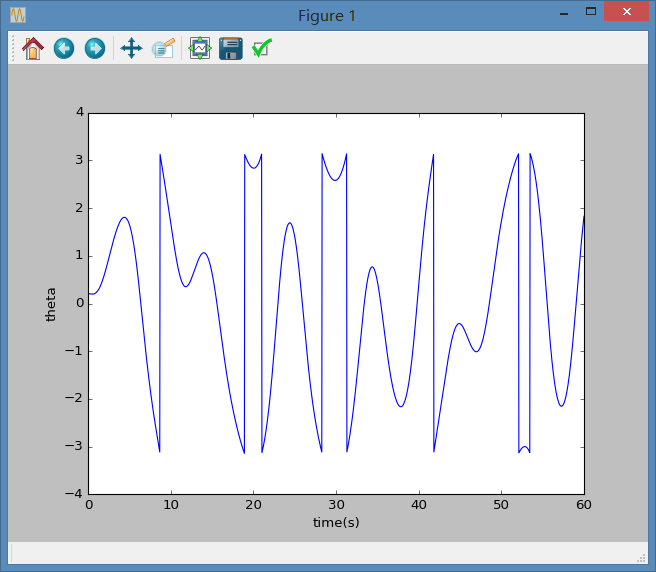
注，与书上图像不尽相同的原因是所取初始角度不同，这里为0.1rad

2.利用semilog函数改变坐标轴标度可以使图像更易于分析，在未用时所做图像如下，此为$F_D=0.5$时：

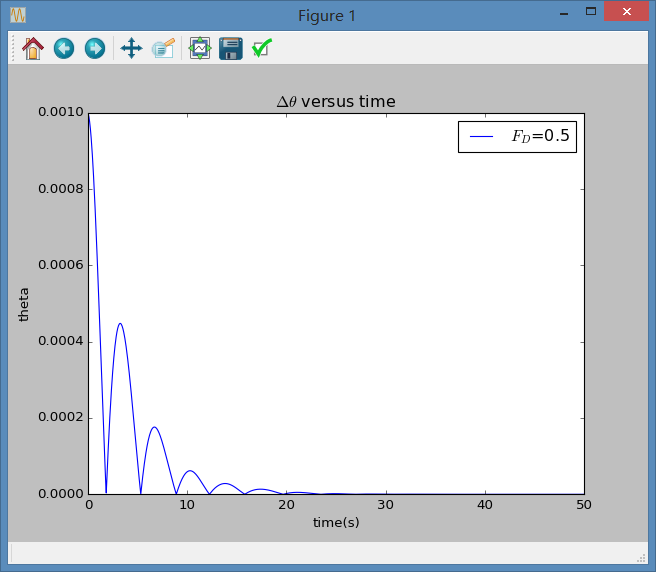
下面为修改后的图像，差异明显

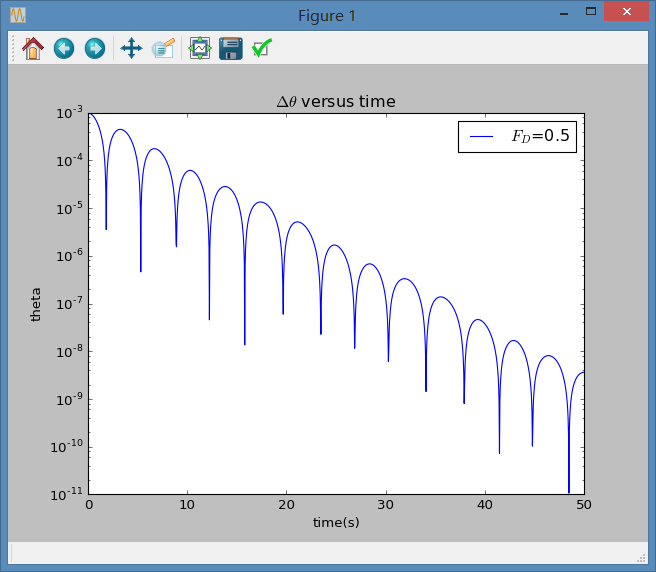
鸣谢

1.张梓桐同学提供了函数pl.semilog，使程序可以改变纵坐标轴的刻度值
2.参考网页http://ieroot.com/2014/05/07/1566.html学习了绘图技巧