计算物理第十一次作业Problem4.19

---

摘要

上次作业我们研究了太阳系中行星的运动轨迹，并且验证了开普勒第三定律，而此次作业我们将重点放在研究土星第七卫星Hyperion的混沌状态上。

背景

Hyperion就是土卫七，围绕着土星运转，1848年9月16日发现，而其形状如同一个哑铃，因此我们便可以将其模拟为一个质量分布在两端中间由无质量轻杆连接的哑铃模型，重力对其中一端质点m1的作用为：

$$\begin{eqnarray*} \vec F_1=-\frac{GM_{Sat} m_1}{r_1^3}(x_1\vec i +y_1 \vec j) \end{eqnarray*}$$
其中$M_{Sat}$是土星质量，取质心坐标$(x_c,y_c)$，可得：
$$\begin{eqnarray*} \vec \tau_1=[(x_1-x_c)\vec i +(y_1-y_c)\vec j]\times \vec F_1 \end{eqnarray*}$$
同理对于$\vec \tau_2$形式也是相同的，作用于模型上的力矩为$\vec \tau_1+\vec \tau_2$，故可得：
$$\begin{eqnarray*} \frac{d\vec w}{dt}=\frac{\vec \tau_1+\vec \tau_2}{I} \end{eqnarray*}$$
其中 $I=m_1|r_1|^2+m_2|r_2|^2$ 为转动惯量，处理可得：
$$\begin{eqnarray*} \frac{d\vec w}{dt}\approx -\frac{3GM_sat}{r_c^5} (x_csin\theta-y_ccos\theta)(x_c cos\theta+y_c sin\theta) \end{eqnarray*}$$

正文

1.由背景可得，主体程序为：

import pylab as pl
import matplotlib.pyplot as plt
import math
class Hyperion :
    def __init__(self,i=0,total_time=10, time_step=0.001, radius=1,e=0,a=1):
        self.x=[a*(1+e)]
        self.y=[0]
        self.vx=[0]
        self.vy=[2*math.pi]
        self.r=[radius]
        self.time=total_time
        self.dt=time_step
        self.beta=2
        self.alpha=0
        self.t=[0]
        self.theta=[0]
        self.w=[0]
    def run(self):
        _time=0
        GM=4*(math.pi**2)
        r=1
        while(_time<self.time):
            self.r.append(math.sqrt(pow(self.x[-1],2)+pow(self.y[-1],2)))
            self.vx.append(self.vx[-1]-4*pow(math.pi,2)*(1+self.alpha/pow(self.r[-1],2))*self.x[-1]/pow(self.r[-1],1+self.beta)*self.dt)
            self.x.append(self.x[-1]+self.vx[-1]*self.dt)
            self.vy.append(self.vy[-1]-4*pow(math.pi,2)*(1+self.alpha/pow(self.r[-1],2))*self.y[-1]/pow(self.r[-1],1+self.beta)*self.dt)
            self.y.append(self.y[-1]+self.vy[-1]*self.dt)
            self.w.append(self.w[-1]-3*GM/(r**5)*(self.x[-1]*math.sin(self.theta[-1])-self.y[-1]*math.cos(self.theta[-1]))*\
                   (self.x[-1]*math.cos(self.theta[-1])+self.y[-1]*math.sin(self.theta[-1]))*self.dt)
            self.theta.append(self.dt*self.w[-1]+self.theta[-1])
            while self.theta[-1]>=1*math.pi:
                self.theta[-1]=self.theta[-1]-2*math.pi
            while  self.theta[-1]<=-1*math.pi:
                self.theta[-1]=self.theta[-1]+2*math.pi 
            self.t.append(_time)            
            _time += self.dt
    def show_results(self):
        #pl.plot(self.x,self.y)
        plt.plot(self.t,self.w)
        plt.xlabel('x(AU)')
        plt.ylabel('y(AU)') 
        plt.legend()
        plt.title('Hyperion $\\theta$ versus time')
        plt.show()
a = Hyperion()
a.run()
a.show_results()  

运行程序可得：

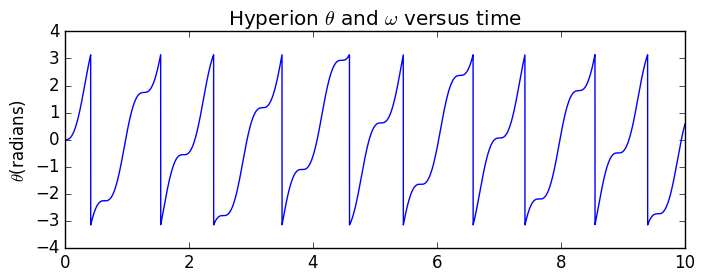
上运行结果为圆轨道时所示结果改变代码$\omega$为$\theta$可得：

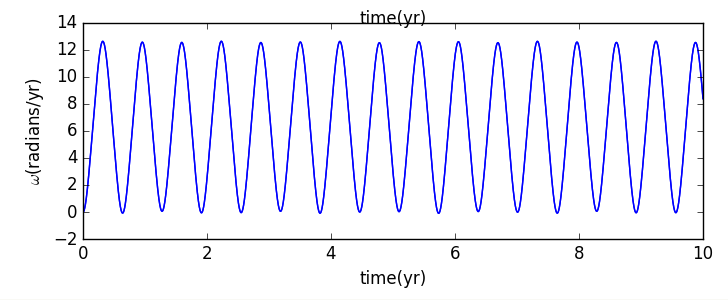
由此看出运动比较规则，同时改变离心率可得椭圆轨道图像为：


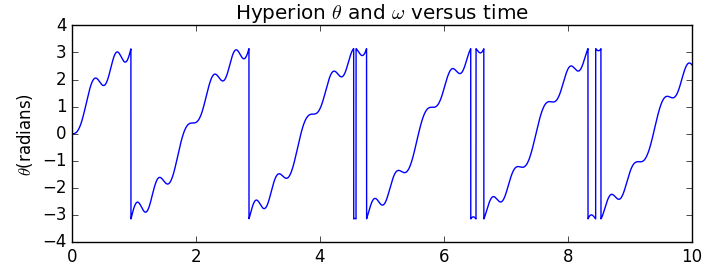
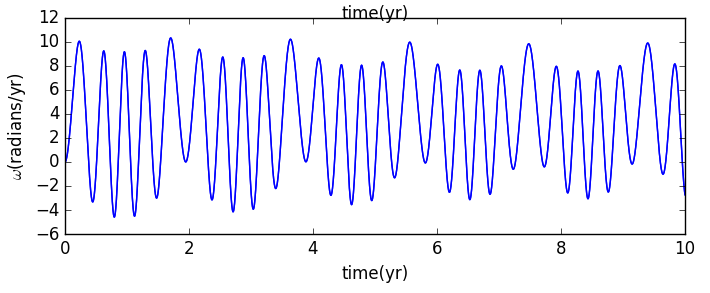
此时图像已经不再规则。
2.改变初始速度可得到运行图像为：



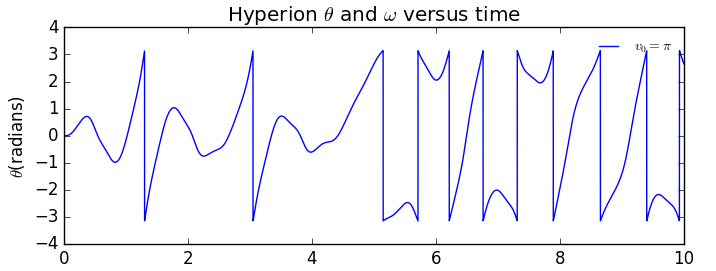
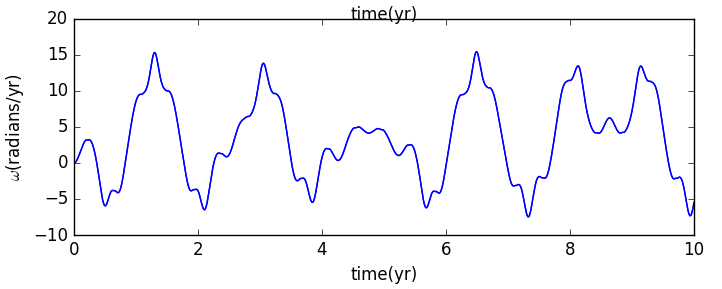
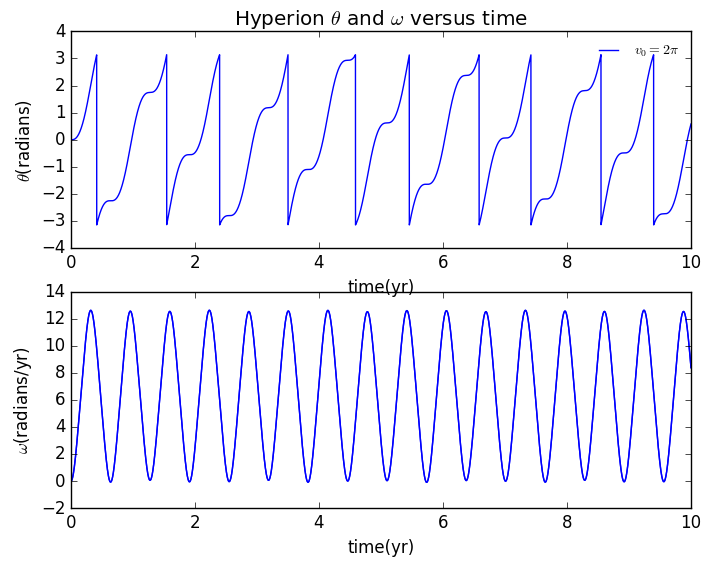
由此看出当初始速度为2π时轨道是规则的。
3.改变$\Delta\theta$的值可得：

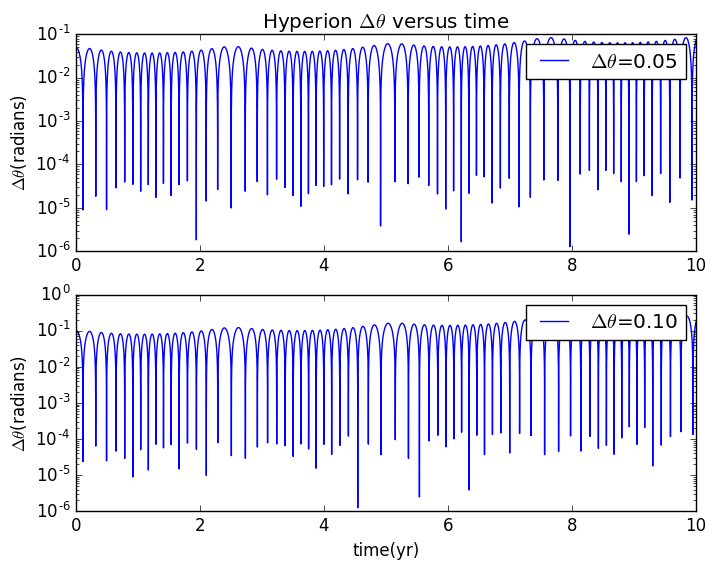
结论

对于Hyperion来说，离心率变化时，当转动轨道为圆时，$\omega、\theta$均有周期，但是当运行轨道变为椭圆，便会出现混沌现象。

致谢

由于个人电脑上Spyder被自己摸索崩溃，于是借用了宗玥同学的电脑，感谢宗玥同学的帮助。