张梓桐计算物理第六次作业

1.Problem

2.10

2.Abstract

In this passage,we are going to discuss the track of a cannon shell with adbiatic effect and wind resistance(headwind,or tailwind).Additionally,a calculation of minimun velocity with regard to a specific target is presented too.

3.Background Introduction

With the previous knowledge of Euler Method,we don't have to illustrate again the basic knowledge.What is of great importance to us is the additional wind resistance.Here we set the velocity of wind to be $\vec v_{wind}$,and the veloocity of cannon to be $\vec v$.
The components of the drag force can be represented as:

$$\begin{eqnarray*} F_{drag,x}=-B_{2}|\vec v-\vec v_{wind}|(v_{x}-v_{wind,x}) \end{eqnarray*}$$
$$\begin{eqnarray*} F_{drag,y}=-B_{2}|\vec v-\vec v_{wind}|(v_{y}-v_{wind,y}) \end{eqnarray*}$$
Noticing that the drag coefficient regarding to the velocity of cannon $\vec v$ is presented in the follow figure.

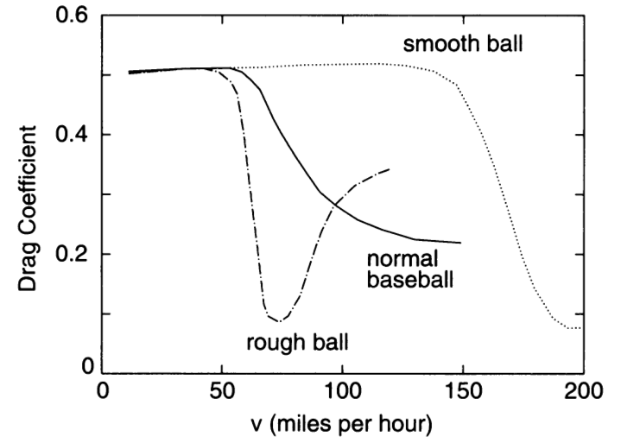
The analyatic form of $B_{2}$ can be expressed as:

$$\begin{eqnarray*} \frac{B_{2}}{m}=0.0039+\frac{0.0058}{1+e^{\frac{v-v_{d}}{\Delta}}} \end{eqnarray*}$$
Here $v_{d}$ and $\Delta$ are constant,$v_{d}=35m/s$ and $\Delta=5m/s$.
On top of that,there will be a effect of adbiatic air effect with regard to the altitude:
$$\begin{eqnarray*} F_{drag}^{*}=F(y=0)\frac{\rho}{\rho_{0}} \end{eqnarray*}$$
In the situation of adbiatic effect:
$$\begin{eqnarray*} \rho(y)=\rho_{0}(1-\frac{ay}{T_{0}})^{\alpha} \end{eqnarray*}$$
which means there will be a additional coefficient plus the wind resistance force.
$$\begin{eqnarray*} F_{drag,x}=-\frac{\rho}{\rho_{0}}B_{2}|\vec v-\vec v_{wind}|(v_{x}-v_{wind,x}) \end{eqnarray*}$$
$$\begin{eqnarray*} F_{drag,y}=-\frac{\rho}{\rho_{0}}B_{2}|\vec v-\vec v_{wind}|v_{y} \end{eqnarray*}$$
Having discussed all of the concerning factors,we finally deduce the core calculation equation:
$$\begin{eqnarray*} v_{x,i+1}=v_{x,i}-\frac{F_{drag,x}}{m}\Delta t \end{eqnarray*}$$
$$\begin{eqnarray*} v_{y,i+1}=v_{y,i}-\frac{F_{drag,y}}{m}\Delta t-g\Delta t \end{eqnarray*}$$
$$\begin{eqnarray*} x_{i+1}=x_{i}+v_{x,i}\Delta t\quad v_{x,i+1}=v_{x,i} \end{eqnarray*}$$
$$\begin{eqnarray*} y_{i+1}=y_{i}+v_{y,i}\Delta t\quad v_{y,i+1}=v_{y,i}-g\Delta t \end{eqnarray*}$$

4.Main body

4.1 The track of the cannon shell.

import math
import pylab as pl
a=1
class cannon:
    def __init__(self,intial_velocity,intial_angle,velocity_of_wind,angle_of_wind):#Variable that can be set#
        self.x=[0]
        self.y=[0] 
        time_step=0.01
        mass=10
        intial_vx=intial_velocity*math.cos(int(intial_angle)*math.pi/180)
        intial_vy=intial_velocity*math.sin(int(intial_angle)*math.pi/180)
        self.vx=[intial_vx]
        self.vy=[intial_vy] 
        self.v=[math.sqrt(intial_vx**2+intial_vy**2)]
        self.dt=time_step
        self.intial_angle=intial_angle
        self.m=mass
        self.angle_of_wind=angle_of_wind
        self.velocity_of_wind=velocity_of_wind
        self.B2=[self.m*(0.0039+0.0058/(1+math.exp((self.v[0]-35)/5)))] 
        self.delta_v_mold=[math.sqrt((intial_vx-self.velocity_of_wind*math.cos(self.angle_of_wind*math.pi/180))**2+(intial_vy-self.velocity_of_wind*math.sin(self.angle_of_wind*math.pi/180))**2)]
    def run(self):
        i=0  
        while self.y[i]>=0:
            self.B2.append(self.m*(0.0039+0.0058/(1+math.exp((self.v[i]-35)/5))))          
            self.v.append(math.sqrt(abs(self.vx[i])**2+abs(self.vy[i])**2))
            self.delta_v_mold.append(math.sqrt((self.vx[i]-abs(self.velocity_of_wind*math.cos(self.angle_of_wind*math.pi/180)))**2+(self.vy[i]-self.velocity_of_wind*math.sin(self.angle_of_wind*math.pi/180))**2))
            self.x.append(self.x[i]+self.vx[i]*self.dt)
            self.y.append(self.y[i]+self.vy[i]*self.dt)
            self.vx.append(self.vx[i]-pow(1-0.0065*self.y[i]/273,2.5)*self.B2[i]*self.delta_v_mold[i]*(self.vx[i]-self.velocity_of_wind*math.cos(self.angle_of_wind*math.pi/180))/self.m*self.dt)
            self.vy.append(self.vy[i]-10*self.dt-pow(1-0.0065*self.y[i]/273,2.5)*self.B2[i]*self.delta_v_mold[i]*(self.vy[i]-self.velocity_of_wind*math.sin(self.angle_of_wind*math.pi/180))/self.m*self.dt)
            i+=1
        self.x[-1]=(self.x[-1] * self.y[-2] - self.x[-2] * self.y[-1])/ (self.y[-2] - self.y[-1])figure_2.png-74.6kB
    def show(self):
        pl.plot(self.x,self.y,label='$\\theta=$'+str(self.intial_angle)+'$^{\circ}$'+'.x='+str(int(self.x[-1]))+',Wind velocity '+str(self.velocity_of_wind)+'\n'+'Angle of wind is '+str(self.angle_of_wind)+'$^{\circ}$')
        pl.ylim(0,300) 
        pl.xlim(0,400)
        pl.xlabel('x(m)')
        pl.ylabel('y(m)')
        pl.show()
        pl.legend(fontsize='xx-small')
class show_trajectory_of_various_angle(cannon):
    def run2(self):
        theta=0
        while theta<90:
            a=cannon(intial_angle=theta,intial_velocity=110,velocity_of_wind=10,angle_of_wind=135)            
            theta+=1
            a.run()
            a.show()
class show_trajectory_of_various_wind_velocity(cannon):
    def run3(self):
        v=0
        while v<30:
            b=cannon(intial_velocity=110,intial_angle=45,velocity_of_wind=v,angle_of_wind=135)
            v+=1
            b.run()
            b.show()
class show_trajectory_of_various_angle_of_wind(cannon):
    def run4(self):
        theta2=45
        while theta2 in [45,135]:
            c=cannon(intial_velocity=244,angle_of_wind=theta2,intial_angle=35,velocity_of_wind=22.27)
            theta2+=135
            c.run()
            c.show() 
a=show_trajectory_of_various_angle(110,45,10,135)
a.run2()      

4.2 Find the minimun firing velocity

import math
import pylab as pl
import time
a=1
class cannon:
    def __init__(self,intial_velocity,intial_angle,velocity_of_wind,angle_of_wind):#Variable that can be set#
        self.x=[0]
        self.y=[0] 
        time_step=0.01
        mass=10
        intial_vx=intial_velocity*math.cos(int(intial_angle)*math.pi/180)
        intial_vy=intial_velocity*math.sin(int(intial_angle)*math.pi/180)
        self.vx=[intial_vx]
        self.vy=[intial_vy] 
        self.v=[math.sqrt(intial_vx**2+intial_vy**2)]
        self.dt=time_step
        self.intial_angle=intial_angle
        self.m=mass
        self.angle_of_wind=angle_of_wind
        self.velocity_of_wind=velocity_of_wind
        self.B2=[self.m*(0.0039+0.0058/(1+math.exp((self.v[0]-35)/5)))] 
        self.delta_v_mold=[math.sqrt((intial_vx-self.velocity_of_wind*math.cos(self.angle_of_wind*math.pi/180))**2+(intial_vy-self.velocity_of_wind*math.sin(self.angle_of_wind*math.pi/180))**2)]
    def run(self):
        i=0  
        while self.y[i]>=-100:
            self.B2.append(self.m*(0.0039+0.0058/(1+math.exp((self.v[i]-35)/5))))          
            self.v.append(math.sqrt(abs(self.vx[i])**2+abs(self.vy[i])**2))
            self.delta_v_mold.append(math.sqrt((self.vx[i]-abs(self.velocity_of_wind*math.cos(self.angle_of_wind*math.pi/180)))**2+(self.vy[i]-self.velocity_of_wind*math.sin(self.angle_of_wind*math.pi/180))**2))
            self.x.append(self.x[i]+self.vx[i]*self.dt)
            self.y.append(self.y[i]+self.vy[i]*self.dt)
            self.vx.append(self.vx[i]-pow(1-0.0065*self.y[i]/273,2.5)*self.B2[i]*self.delta_v_mold[i]*(self.vx[i]-self.velocity_of_wind*math.cos(self.angle_of_wind*math.pi/180))/self.m*self.dt)
            self.vy.append(self.vy[i]-10*self.dt-pow(1-0.0065*self.y[i]/273,2.5)*self.B2[i]*self.delta_v_mold[i]*(self.vy[i])/self.m*self.dt)
            i+=1
        self.x[-1]=((-100-self.y[-1])*(self.x[-1]-self.x[-2])/(self.y[-1]-self.y[-2]))+self.x[-1]
        self.y[-1]=-100
        global a        
        a=self.x[-1]
    def show(self):
        pl.plot(self.x,self.y,'r',label='$\\theta=$'+str(self.intial_angle)+'$^{\circ}$'+'.x='+str(int(self.x[-1]))+',Wind velocity '+str(self.velocity_of_wind)+'\n'+'Angle of wind is '+str(self.angle_of_wind)+'$^{\circ}$')
        pl.ylim(-100,300)
        pl.xlabel('x(m)')
        pl.ylabel('y(m)')
        pl.show()
        pl.legend(fontsize='xx-small')
class find_spot(cannon):
    object_x=220
    object_y=-100
    def run4(self):
        v=67.7230
        while 67.7230<=v<68:
            theta2=14.99
            while 14.99<=theta2<20:
                c=cannon(intial_velocity=v,angle_of_wind=135,intial_angle=theta2,velocity_of_wind=10)
                c.run()
                if 220>a:
                    theta2+=0.0001
                else:
                    print theta2,'degree',a,'m',v,'m/s'
                    break
            v+=0.00001
            if 220<a:
                  break
a=find_spot(110,45,10,135)
a.run4()      

5.Track Result

5.1 Result with different intial angles

Here we set the intial velocity all to be $110m/s$.The angle of wind is $135^{\circ}$(headwind),and the velocity of wind is $10m/s$

Now we change the intial firing angles from $(0^{\circ},90^{\circ})$ with $d\theta=1^{\circ}$

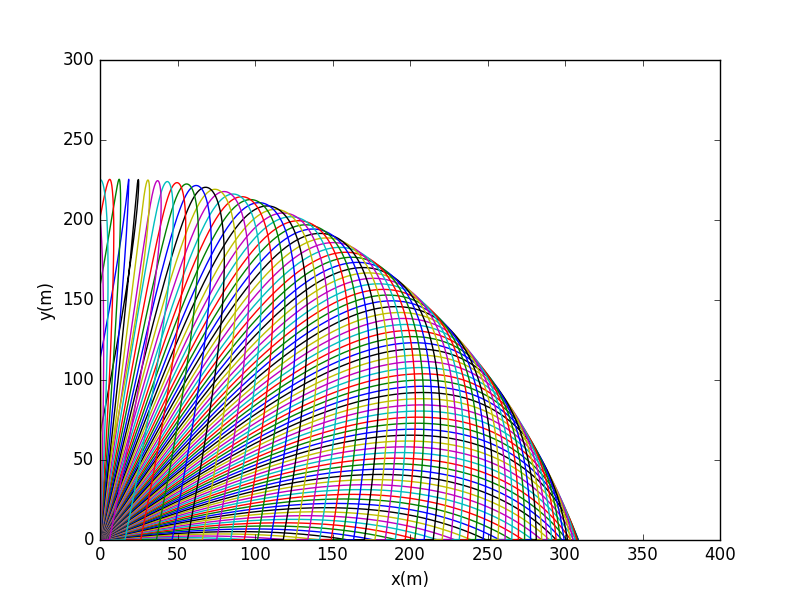
As this figure is not too compact and difficult to distinguish,we now set $d\theta=15^{\circ}$

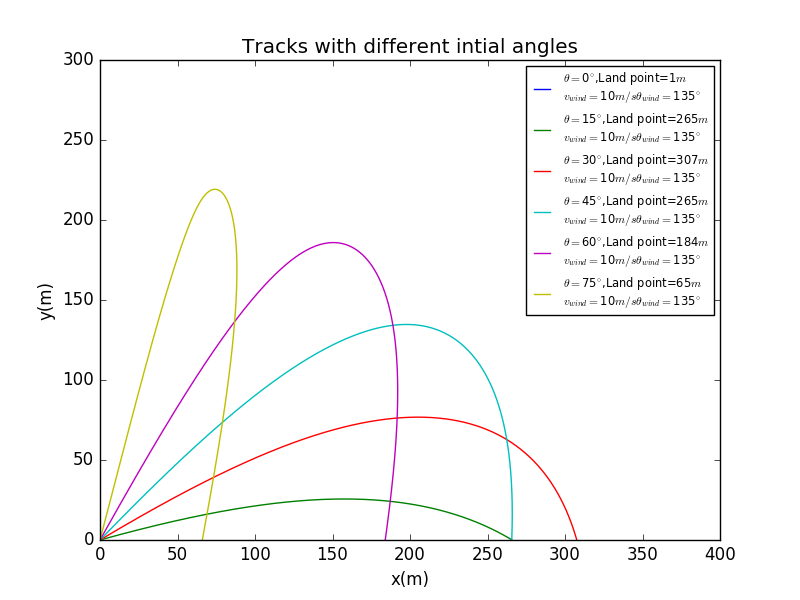
Here we can see,around $\theta=30^{\circ}$,the land point reachs max.
Now we take a closer look at $\theta$ around $30^{\circ}$.

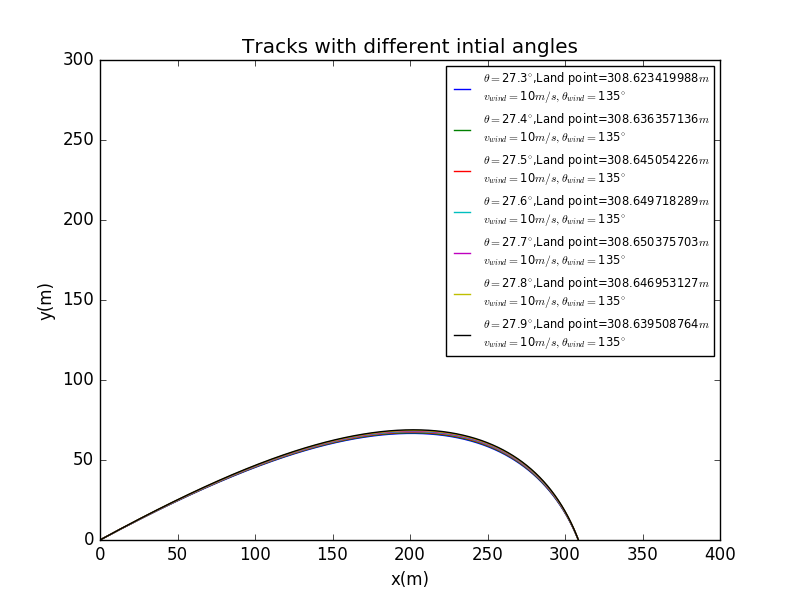
Here we can see, at around $\theta = 27.7^{\circ}$,the land point reaches the maxium.And $x_{max}=308.650m$.

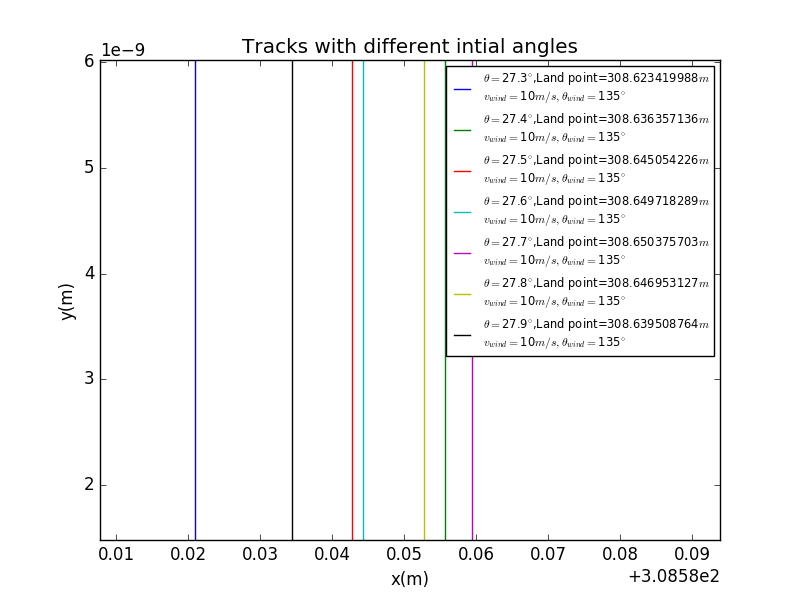
5.2 Results with different wind angles

Here we set the intial velocity all to be $110m/s$.The angle of wind is $[0^{\circ},180^{\circ}]$(from tailwind to headwind),$d\theta=2^{\circ}$,and the velocity of wind is $10m/s$.Intial angles is $45^{\circ}$.

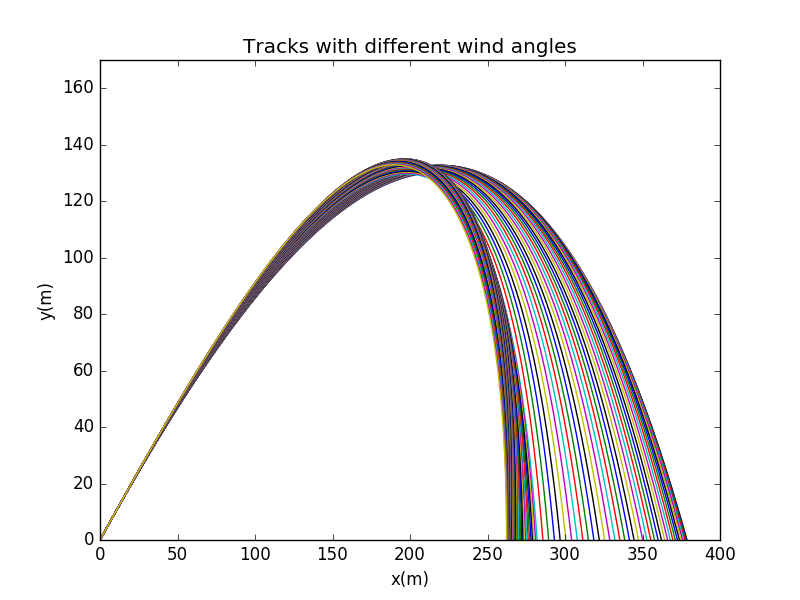
Here we can see,as the angles of wind is changed from tailwind to headwind, the land point is shifting left,which means reach a lesser distance.

To illustrate the difference with or withoud wind,I am going to attach another figure.The angle of wind is $0^{\circ}$ and $180^{\circ}$

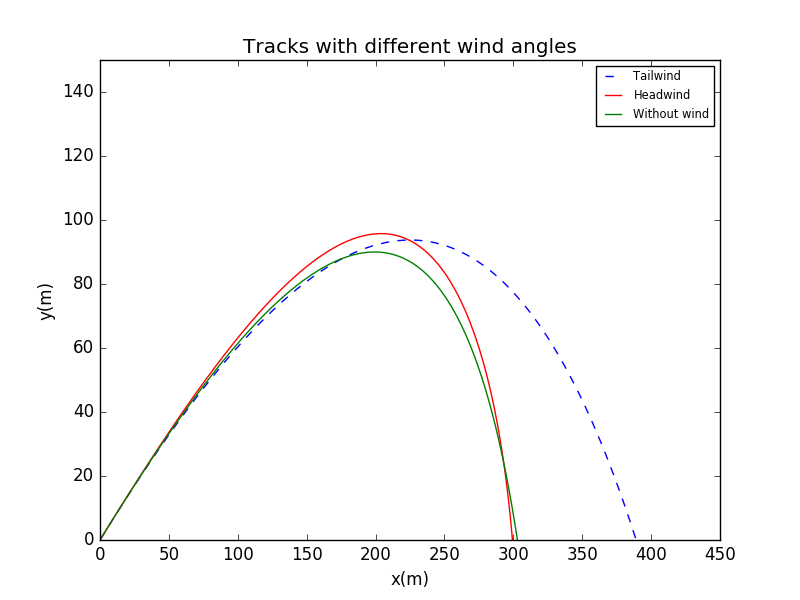
This figure corresponds well to our feeling in our life!

5.3 Results with different velocity of wind

Here we set the intial velocity all to be $110m/s$.The angle of wind is $135^{\circ}$(headwind),and the velocity of wind is $[0m/s,25m/s]$,$dv=1m/s$. Intial angles is $45^{\circ}$.

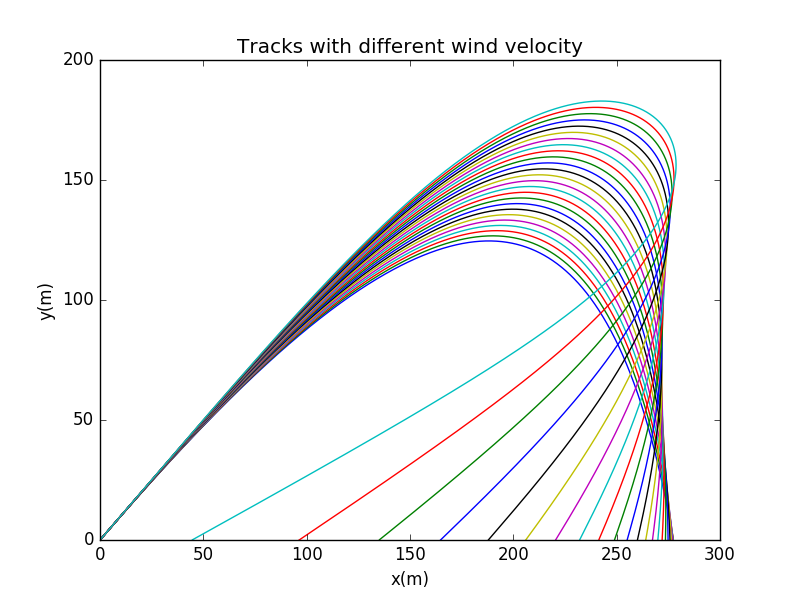
As the wind velocity is becoming larger and larger,there may be situation where the cannon shell is blown back.

6.Find the target

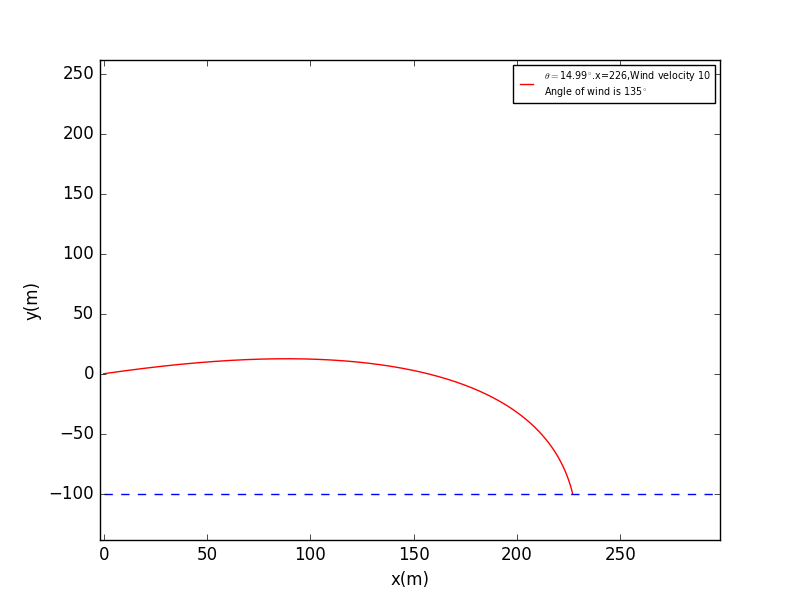
In this section,we are going to discuss about how to fire a cannon shell with the minimun velocity to reach the target.At first,we set the objec to be set in $(220,-100)$,which means the target is lower than the firing places.
However,when we are about to set the scanning interval of $\theta \in(-arctan\frac{10}{220}^{\circ},90^{\circ})$ and velocity $|\vec v| \in (0,500m/s)$ with $d\theta=0.01^{\circ}$ and $d|\vec v|=0.1m/s$.The time taken by the calculation is too long.For compromising,we set the $d\theta=1^{\circ}$ and $d|\vec v|=1m/s$ to identify the mighty intervals,and we find around $\theta=15^{\circ}$ and velocity about $67m/s$ is the ideal result.
Step by step,we narrow the section and finally finds out that at $|\vec v|=67.723m/s$ and $\theta=14.999^{\circ}$ ,the velocity reaches the minmum.

7.Acknowledgement

1.Yu kang has helped with the find-spot programming.
2.Matplotlib.