计算物理第五次作业2.9

摘要

这道题主要是要计算以一定速度和角度发射的大炮的运动轨迹，而相对于书上，此题要考虑空气阻力和空气密度随海拔高度变化，并求出相应的哪个角度大炮所运动的轨迹最远。

背景介绍

抛体运动是物理问题中一个很重要的模型，而用Python语言写出相应的程序解决具体问题也是学习后的具体应用体现。

正文

首先将空气阻力简单表示成 Fdrag=-Bv^2

而且空气密度随海拔变化为p= p0exp(-y/y0)

因此阻力可表示为Fdrag=p/p0*Fdrag(y=0)

同时根据Euler法模拟自行车运动问题和理想状态不受阻力情况下大炮运动轨迹，因此程序可写为：

import pylab as pl
import math
class  Trajectory_of_cannon:
    """
    Calculate the trajectory of the cannon shell including
    both air drag and the reduced air density at high altitudes.
    """
    def __init__(self,time_step=0.05,X=0,Y=0,initial_speed=700,initial_angel=30):
        self.theta=initial_angel
        self.Vx=[math.cos(self.theta*math.pi/180)*700]
        self.Vy=[math.sin(self.theta*math.pi/180)*700]
        self.X=[0]
        self.Y=[0]
        self.dt=time_step
        self.t=[0]
    def calculate(self):
        i=0
        while self.Y[i]>=0:                  
            V=math.sqrt(math.pow(self.Vx[i],2)+math.pow(self.Vy[i],2))
            temp_X=self.X[i]+self.Vx[i]*self.dt
            temp_Y=self.Y[i]+self.Vy[i]*self.dt
            self.X.append(temp_X)
            self.Y.append(temp_Y)
            temp_Vx=self.Vx[i]-math.exp(-self.Y[i]/10000)*0.00004*V*self.Vx[i]*self.dt
            temp_Vy=self.Vy[i]-9.79*self.dt-math.exp(-self.Y[i]/10000)*0.00004*V*self.Vy[i]*self.dt
            self.Vx.append(temp_Vx)
            self.Vy.append(temp_Vy)
            self.t.append(self.t[i]+self.dt)
            i+=1
    def show_result(self):     
        pl.plot(self.X,self.Y)
        pl.xlabel("X(m)")
        pl.ylabel("Y(m)")
        pl.xlim(0,30000)
        pl.ylim(0,20000)
        pl.show()
    def landing_point(self):              
       self.angel_point=dict()
       self.angel_point[self.theta]=self.X[-1]-self.Y[-1]*(self.X[-1]-self.X[-2])/(self.Y[-1]-self.Y[-2])
       print(self.angel_point)
a=Trajectory_of_cannon()     
a.calculate()
a.show_result() 
a.landing_point() 
class Maximum_of_range(Trajectory_of_cannon):   
     def line_of_different_angel(self): 
         self.theta=0
         for i in range(91):
             b=Trajectory_of_cannon(initial_angel=self.theta) 
             b.calculate()
             b.show_result()
             b.landing_point()
             self.theta=self.theta+1
b=Maximum_of_range()
b.line_of_different_angel() 

此为角度为25度时的轨迹图像：

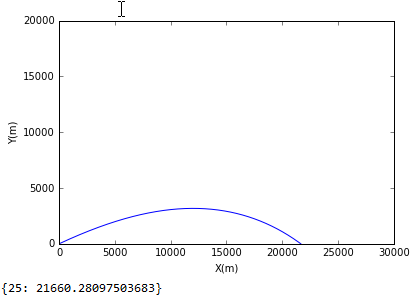
此为角度为50度是的轨迹图像：

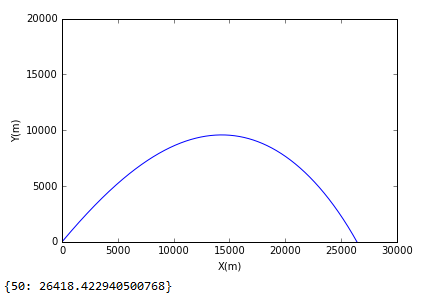
由于个人知识储备的不足，无法将所有的运动的轨迹整合在一个图片上，但通过查看结果，可看出当角度为46度时大炮运动的轨迹最远。其轨迹图为：

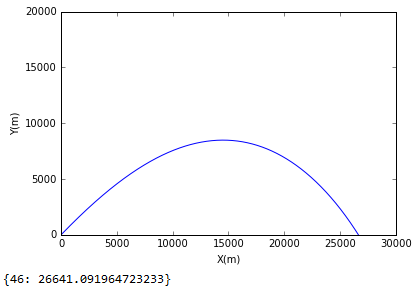
结论

当考虑空气阻力和空气密度时，大炮的发射角度为46度时运动的轨迹最远。同时不会将所有轨迹整合在一起仍然需要自己慢慢去学习。

致谢

谢谢陆文龙同学作业给予的帮助。