计算物理第八次作业Problem3.18

---

摘要

上次作业是研究微小变量对混沌系统的影响，而Problem3.18是研究连续改变$F_D$时对混沌现象的影响。

背景

由书可知，周期加倍时：

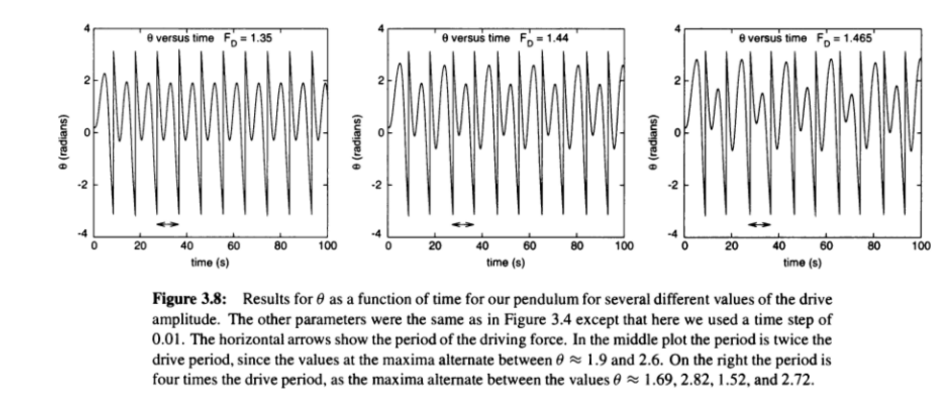
而Bifurcation diagram（分岔图）为：

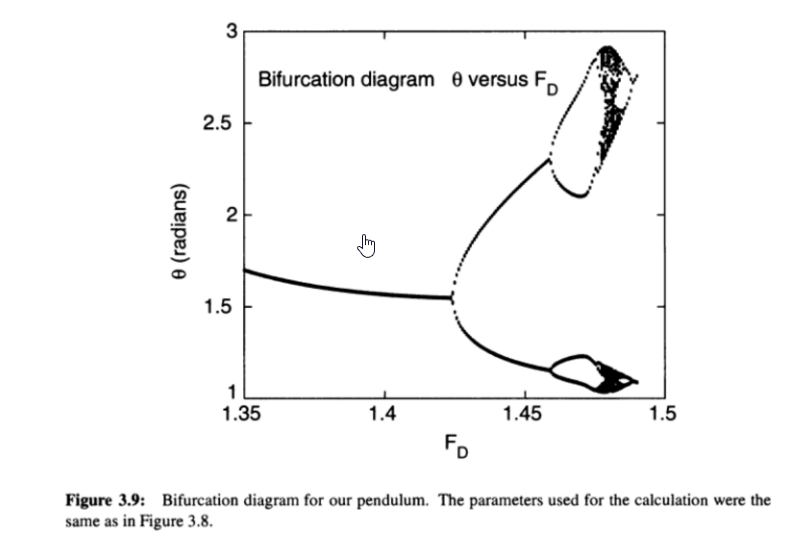
过渡点为

$$F_D\approx1.424,F_D\approx1.459$$
Feigenbaum $\delta$:
$$\delta \equiv \frac{F_n-F_{n-1}}{F_{n+1}-F_{n}}$$

正文

程序为:

import pylab as pl
import math
class Simple_Pendulum :
    def __init__(self,i=0,initial_theta=0.2,time_step=0.04,total_time=50000,length=9.8,\
                 g=9.8, initial_omega=0,q=0.5,Fd=1.2,omegaD=0.66667):
        self.theta=[initial_theta]
        self.theta0=[initial_theta]
        self.t=[0]
        self.omega=[initial_omega]
        self.dt=time_step
        self.time=total_time
        self.g=g 
        self.l=length
        self.q=q
        self.Fd=Fd
        self.omegaD=omegaD
        self.a=[0]
        self.b=[0]
    def run(self):
        _time=0
        while(_time<self.time):
            self.omega.append(self.omega[-1]-((self.g/self.l)*math.sin(self.theta[-1])+\
                 self.q*self.omega[-1]-self.Fd*math.sin(self.omegaD*self.t[-1]))*self.dt)            
            self.theta.append(self.theta[-1]+self.omega[-1]*self.dt)
            self.t.append(_time)            
            _time += self.dt
            if(self.theta[-1]>=math.pi):
                self.theta[-1]=self.theta[-1]-2*math.pi
            if(self.theta[-1]<=-math.pi):
                self.theta[-1]=self.theta[-1]+2*math.pi
            if((self.t[-1])%(2*math.pi/self.omegaD)<0.01 ):
                self.a.append(self.omega[-1])
                self.b.append(self.theta[-1])
    def show_results(self):
        pl.plot(self.b,self.a,'.',label='$F_{D}$=1.2')
        pl.xlabel('$\\theta$(rad)')
        pl.ylabel('$\omega$(rad)')
        pl.legend()
        pl.title('$\omega$ versus $\\theta$ ' )
        pl.show()        
a = Simple_Pendulum()
a.run()
a.show_results()  

运行结果为：

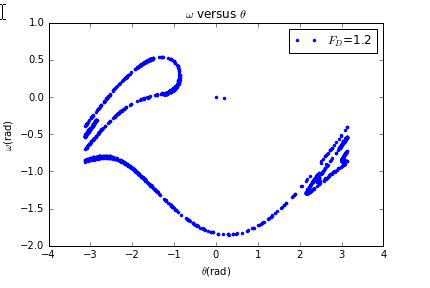
当然可以改变$F_D$的值，如$F_D=1.3$时：

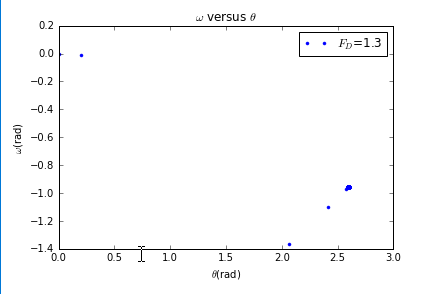
$F_D=1.4$时：

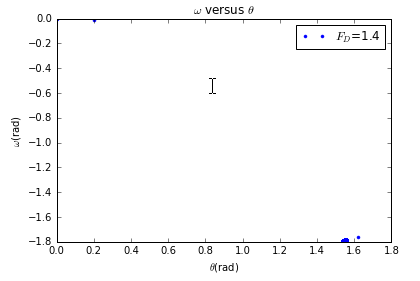
结论

混沌效应只在特殊$F_D$值附近出现。

备注

不知是否是电脑原因，安装Vpython时总是失败，因此没有及时作出程序，实在是失误。

致谢

感谢宗玥同学的耐心帮助。