@zy-0815
2016-10-31T05:16:16.000000Z
字数 2945
阅读 1282
计算物理第七次作业Problem3.14
摘要
这次作业是继续课本上对Lyapunov指数的研究,但是对两个不同的变量有个轻微的减小,观察Lyapunov指数相对于初始值的变化。
背景介绍
此次作业是对混沌系统的进一步研究,即混沌系统对初始值的极端敏感性。
正文
在书上,系统的初始值为
因此初始程序为:
import pylab as plimport mathclass pendulum:def __init__(self, time_step=0.04, theta=0.2,g=9.8,l=9.8,q =0.5,fd=1.2,wd=0.66666):self.ta=thetaself.theta=[theta]self.pi= math.piself.w = [0]self.q = qself.fd = fdself.wd = wdself.wo = g/lself.t = [0]self.dt = time_stepdef run(self):_time = 0while(self.t[-1]<=60):self.w.append(self.w[-1]-(self.wo*math.sin(self.theta[-1])+self.q*self.w[-1]-self.fd*math.sin(self.wd*self.t[-1]))*self.dt)tmp=self.w[-1]-(self.wo*math.sin(self.theta[-1])+self.q*self.w[-1]-self.fd*math.sin(self.wd*self.t[-1]))*self.dtself.theta.append(self.theta[-1] + tmp * self.dt)self.t.append(_time)_time += self.dtif (self.theta[-1] <= -math.pi):self.theta[-1] = self.theta[-1] + self.pi + math.piif (self.theta[-1] >= math.pi):self.theta[-1] = self.theta[-1] - self.pi - math.pidef show_results(self):pl.plot(self.t,self. theta)pl.xlabel(" time($s$)")pl.ylabel("angle($radians$)")pl.title("angle versus time")pl.show()a=pendulum()a.run()a.show_results()
运行可得到初试结果为:
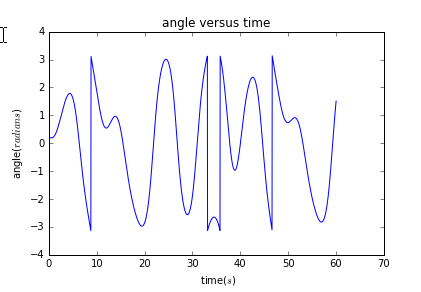
1、使q微量减小
此时可以对进行微量减小,如改变为,则程序为
import pylab as plimport mathclass pendulum:def __init__(self, time_step=0.04, theta1=0.2,theta2=0.2,g=9.8,l=9.8,q1 =0.5,q2=0.499,fd=1.2,wd=0.66666):self.theta1=[theta1]self.theta2=[theta2]self.pi= math.piself.w1 = [0]self.w2 = [0]self.dtheta=[math.fabs(theta1-theta2)]self.q1 = q1self.q2 = q2self.fd = fdself.wd = wdself.wo = g/lself.t = [0]self.dt = time_stepdef run(self):_time = 0while(self.t[-1]<=200):self.w1.append(self.w1[-1]-(self.wo*math.sin(self.theta1[-1])+self.q1*self.w1[-1]-self.fd*math.sin(self.wd*self.t[-1]))*self.dt)tmp1=self.w1[-1]-(self.wo*math.sin(self.theta1[-1])+self.q1*self.w1[-1]-self.fd*math.sin(self.wd*self.t[-1]))*self.dtself.theta1.append(self.theta1[-1] + tmp1 * self.dt)self.w2.append(self.w2[-1]-(self.wo*math.sin(self.theta2[-1])+self.q2*self.w2[-1]-self.fd*math.sin(self.wd*self.t[-1]))*self.dt)tmp2=self.w2[-1]-(self.wo*math.sin(self.theta2[-1])+self.q2*self.w2[-1]-self.fd*math.sin(self.wd*self.t[-1]))*self.dtself.theta2.append(self.theta2[-1] + tmp2 * self.dt)self.dtheta.append(math.log(math.fabs(self.theta1[-1]-self.theta2[-1])))self.t.append(_time)_time += self.dtif (self.theta1[-1] <= -math.pi):self.theta1[-1] = self.theta1[-1] + self.pi + math.piif (self.theta1[-1] >= math.pi):self.theta1[-1] = self.theta1[-1] - self.pi - math.piif (self.theta2[-1] <= -math.pi):self.theta2[-1] = self.theta2[-1] + self.pi + math.piif (self.theta2[-1] >= math.pi):self.theta2[-1] = self.theta2[-1] - self.pi - math.pidef show_results(self):pl.plot(self.t,self.dtheta,"r")pl.xlabel(" time($s$)")pl.ylabel("log(d_angle)($radians$)")pl.title("log(d_angle) versus time")pl.show()a=pendulum()a.run()a.show_results()
运行结果为:
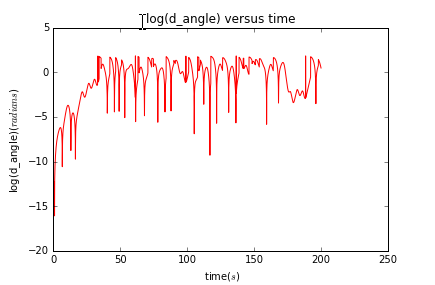
同理对于,运行结果为:
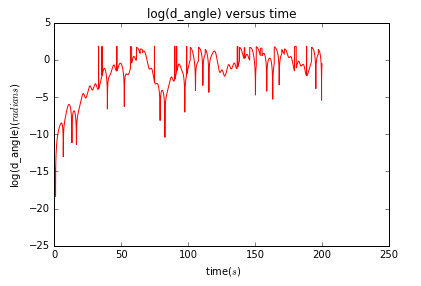
2、使进行微量减小
主程序依旧像上面一样,可以改变使得,带入后运行结果分别为:
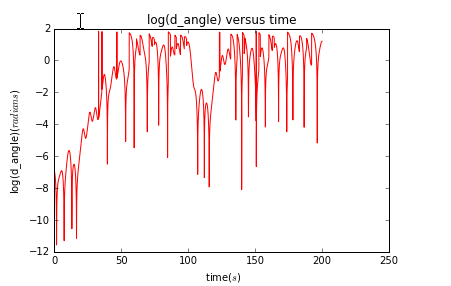

结论
由此可以看出,对于混沌系统,即使变量有着很轻微的变化,Lyapunov指数也会有很明显的变化,混沌系统对于初始值有着很高的敏感性。
致谢
感谢张梓桐同学对于程序不足之处的修改。
