计算物理课后作业Problem1.5

---

摘要

经过一段时间的学习，我们已经掌握了一定的语法和语言，而此次作业就是用Euler法解决常微分方程。

背景

学习计算物理的原因就是学习用计算机解决物理实际问题，而这次作业便是让我们开始解决实际问题，加以应用。

正文

由题可得，方程组为：

$$\begin{eqnarray*} \frac{dN_A}{dt}&=&\frac{N_B}{\tau}-\frac{N_A}{\tau}　　(1)\\　　 \frac{dN_B}{dt}&=&\frac{N_A}{\tau}-\frac{N_B}{\tau}　　(2) \end{eqnarray*}$$
可解得：
$$\begin{eqnarray*} N_A&=&N_B+100e^{-\frac{t}{\tau}}　　　(3)\\ N_B&=&N_A-100e^{-\frac{t}{\tau}}　　　(4) \end{eqnarray*}$$
由第一章PPT可知，Euler method为：
$$\begin{eqnarray*} \frac{dN_U}{dt}=\frac{N_U(t+\Delta t)-N_U(t)}{\Delta t} \end{eqnarray*}$$
于是上两式即为：
$$\begin{eqnarray*} N_A(t+\Delta t)&=&N_A+\frac{N_B-N_A}{\tau}\Delta t　　(5)\\ N_B(t+\Delta t)&=&N_B+\frac{N_A-N_B}{\tau}\Delta t　　(6) \end{eqnarray*}$$
因此学习第一章PPT便可写出代码为：

import pylab as pl
class uranium_decay:
    def __init__(self, number_of_nuclei_A = 100, number_of_nuclei_B = 0, time_constant = 1, time_of_duration = 5, time_step = 0.05):
        # unit of time is second
        self.n_uranium_A = [number_of_nuclei_A]
        self.n_uranium_B = [number_of_nuclei_B]
        self.t = [0]
        self.tau = time_constant
        self.dt = time_step
        self.time = time_of_duration
        self.nsteps = int(time_of_duration // time_step + 1)
        print("Initial number of nuclei A ->", number_of_nuclei_A)
        print("Initial number of nuclei B ->", number_of_nuclei_B)
        print("Time constant ->", time_constant)
        print("time step -> ", time_step)
        print("total time -> ", time_of_duration)
    def calculate(self):
        for i in range(self.nsteps):
            tmp1 = self.n_uranium_A[i] + (self.n_uranium_B[i] - self.n_uranium_A[i]) / self.tau * self.dt
            tmp2 = self.n_uranium_B[i] + (self.n_uranium_A[i] - self.n_uranium_B[i]) / self.tau * self.dt 
            self.n_uranium_A.append(tmp1)
            self.n_uranium_B.append(tmp2)
            self.t.append(self.t[i] + self.dt)  
    def show_results(self):
        plot1, = pl.plot(self.t, self.n_uranium_A,'b')
        plot2, = pl.plot(self.t, self.n_uranium_B,'g')
        pl.title('Nuclei Decay')
        pl.xlabel('time ($s$)')
        pl.ylabel('Number of Nuclei')
        first_legend=pl.legend([plot1, plot2], ['Particle A', 'Particle B'], loc="best")
        pl.show()
a = uranium_decay()
a.calculate()
a.show_results()

结论

（1）运行上面程序可以得出如下结果：

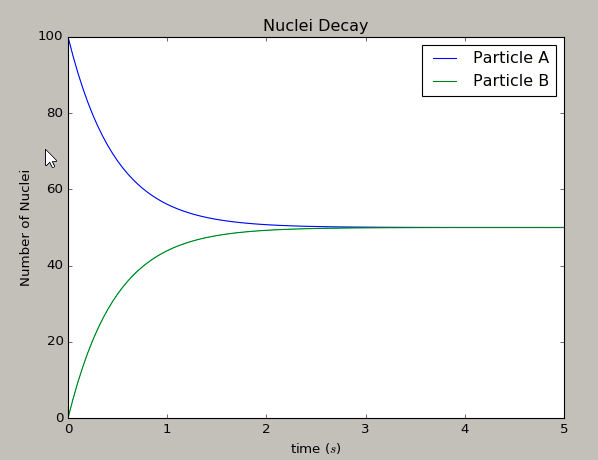
（2）虽然写出了程序，也得出了结果，但是不知道为什么PPT中有些语法的含义，删去之后便可以运行，如a.store_results()。感觉还要自己多查多练。

致谢

感谢宗玥同学提供的作业部落VIP账号，同时告诉我一些LaTeX公式编辑的语法。