计算物理第十一次作业

计算物理

---

摘要

　　本次作业将探究三体运动，并将其应用于对Hyperion运动的分析中，同时探究4.19及4.20相关问题

背景

　　行星的卫星是在太阳系中非常常见，甚至对于土星和木星来说拥有不止一颗卫星，而土星更是有其标志性的土星环而格外美丽。
　　
　　但在众多的卫星当中，有一颗尤为特殊。对于大多数卫星而言，像月球，都是做绕行星的规则运动，甚至对于月球来说，其自转周期和公转周期的吻合使得它永远只有一面朝向地球。可以对于Hyperion来说，这颗土星的卫星之一，其运动却如此与众不同。
　　
　　由于自身形状的特殊性，它只有在两个方向上可以保持稳定的旋转状态，使得这颗土星的卫星并没有一个持续不变的旋转轴线。实际上，它就像一个在轨道上运行的哑铃。
　　我们可以对它进行受力分析如下：
　　首先将其简化成哑铃，两端质量为$m_1$和$m_2$，位置分别为$(x_1,y_1)和(x_2,y_2)$， 受土星引力为$\vec F_1, \vec F_2$， 轴线与x轴成角度$\theta$，则：

$$\begin{eqnarray*} \vec F_1=-\frac{GM_sat m_1}{r_1^3}(x_1\vec i +y_1 \vec j) \end{eqnarray*}$$
　　取质心坐标$(x_c,y_c)$
$$\begin{eqnarray*} \vec \tau_1=[(x_1-x_c)\vec i +(y_1-y_c)\vec j]\times \vec F_1 \end{eqnarray*}$$
对于$\vec \tau_2$有相同形式，则作用于土卫七上的总力矩为$\vec \tau_1+\vec \tau_2$，则有下式可得：
$$\begin{eqnarray*} \frac{d\vec w}{dt}=\frac{\vec \tau_1+\vec \tau_2}{I} \end{eqnarray*}$$
　　其中 $I=m_1|r_1|^2+m_2|r_2|^2$ 为转动惯量。处理上式：
$$\begin{eqnarray*} \frac{d\vec w}{dt}\approx -\frac{3GM_sat}{r_c^5} (x_csin\theta-y_ccos\theta)(x_c cos\theta+y_c sin\theta) \end{eqnarray*}$$
　　其中 $r_c$为土星到质心的距离

正文

主程序如下：

import pylab as pl
import matplotlib.pyplot as plt
import math
class Hyperion :
    def __init__(self,i=0,total_time=10, time_step=0.001, radius=1,e=0,a=1):
        self.x=[a*(1+e)]
        self.y=[0]
        self.vx=[0]
        self.vy=[2*math.pi]
        self.r=[radius]
        self.time=total_time
        self.dt=time_step
        self.beta=2
        self.alpha=0
        self.t=[0]
        self.theta=[0]
        self.w=[0]
    def run(self):
        _time=0
        GM=4*(math.pi**2)
        r=1
        while(_time<self.time):
            self.r.append(math.sqrt(pow(self.x[-1],2)+pow(self.y[-1],2)))
            self.vx.append(self.vx[-1]-4*pow(math.pi,2)*(1+self.alpha/pow(self.r[-1],2))*self.x[-1]/pow(self.r[-1],1+self.beta)*self.dt)
            self.x.append(self.x[-1]+self.vx[-1]*self.dt)
            self.vy.append(self.vy[-1]-4*pow(math.pi,2)*(1+self.alpha/pow(self.r[-1],2))*self.y[-1]/pow(self.r[-1],1+self.beta)*self.dt)
            self.y.append(self.y[-1]+self.vy[-1]*self.dt)
            self.w.append(self.w[-1]-3*GM/(r**5)*(self.x[-1]*math.sin(self.theta[-1])-self.y[-1]*math.cos(self.theta[-1]))*\
                   (self.x[-1]*math.cos(self.theta[-1])+self.y[-1]*math.sin(self.theta[-1]))*self.dt)
            self.theta.append(self.dt*self.w[-1]+self.theta[-1])
            while self.theta[-1]>=1*math.pi:
                self.theta[-1]=self.theta[-1]-2*math.pi
            while  self.theta[-1]<=-1*math.pi:
                self.theta[-1]=self.theta[-1]+2*math.pi 
            self.t.append(_time)            
            _time += self.dt
    def show_results(self):
        #pl.plot(self.x,self.y)
        plt.plot(self.t,self.w)
        plt.xlabel('x(AU)')
        plt.ylabel('y(AU)') 
        plt.legend()
        plt.title('Hyperion $\\theta$ versus time')
        plt.show()
a = Hyperion()
a.run()
a.show_results()  

结论

1. 圆轨道中

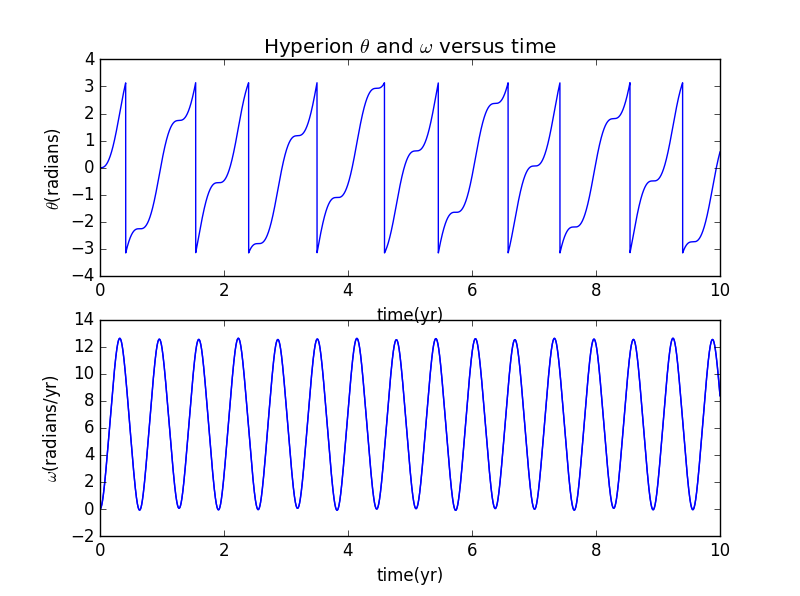
显然此时的运动还是规则的

2. 椭圆轨道

此时取$e=0.206$，则得到下图

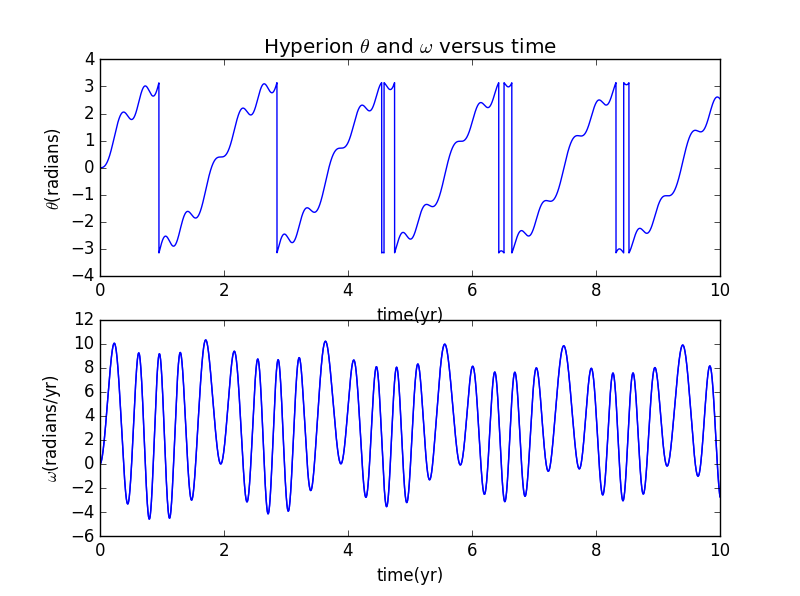
显然这个时候的运动不再规律，我们可进一步研究不同初始条件下，它的运动情况
2.1 偏心率的影响



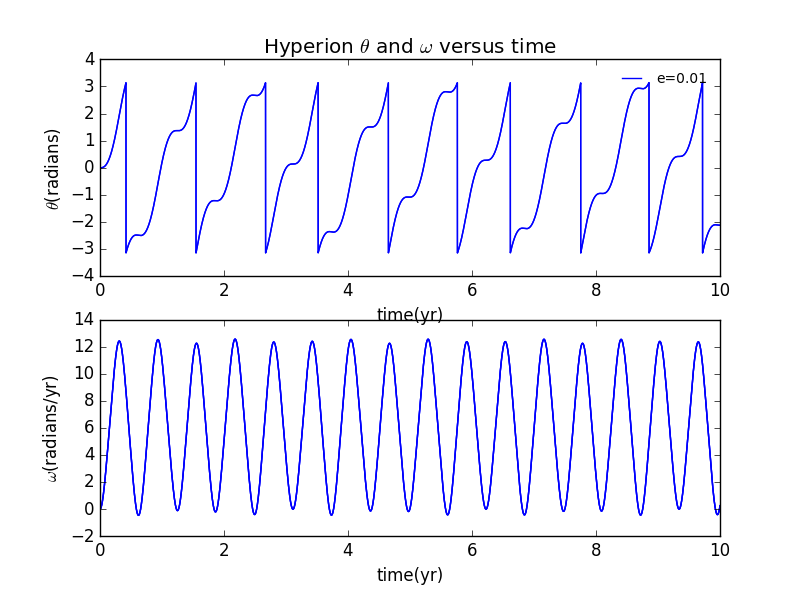
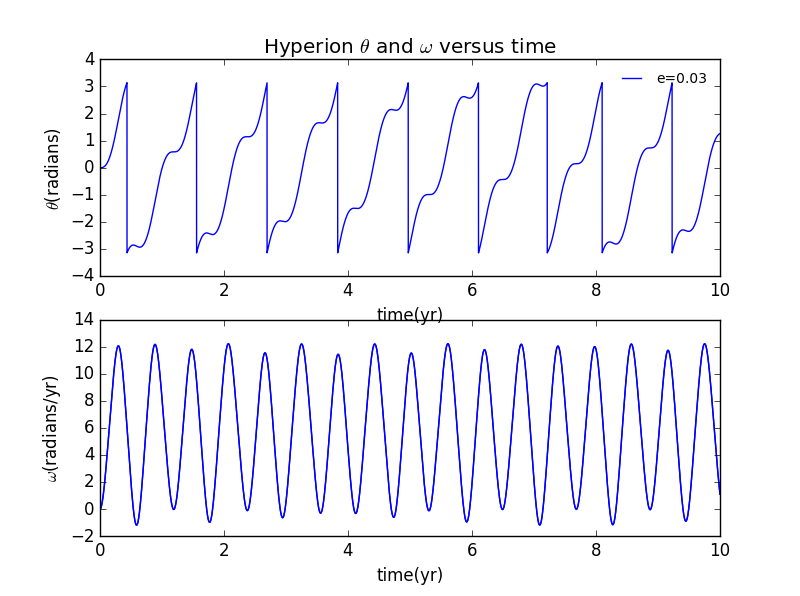
可见当$e=0.03$时，有扰动迹象，到$e=0.05$，运动已经开始混乱
2.2 初速度的影响



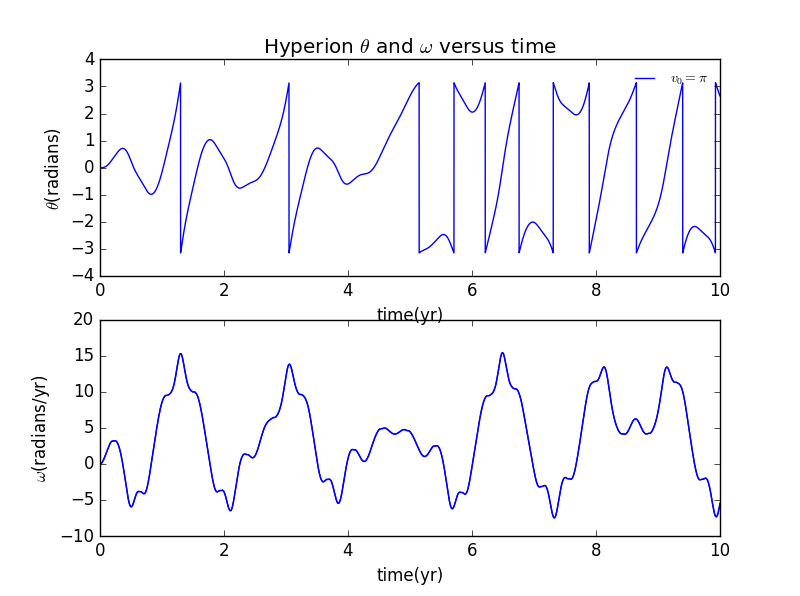
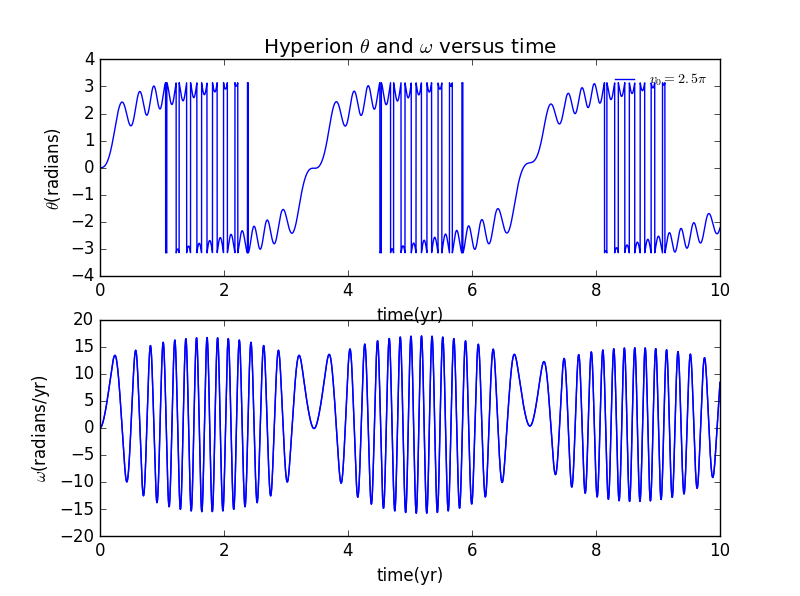
显然只有$2\pi$时的运动是稳定的，而实际运动中，也只有合适的速度才能使其绕轨运动，速度的改变会直接影响其轨道。

3 初始$\theta$值

　　3.1 改变$e$的初始值
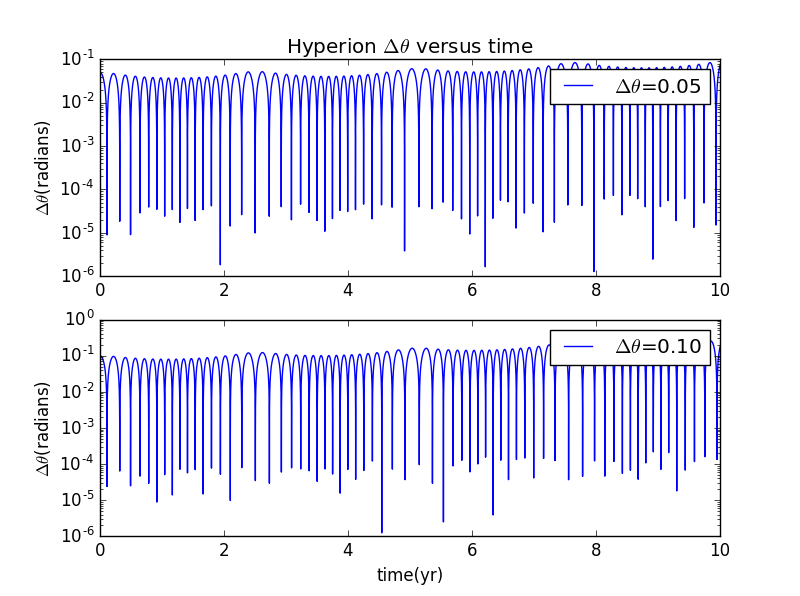
　　我们可以做$\Delta \theta$与$t$的图像，通过Lyapunov指数的变化来研究其运动规律


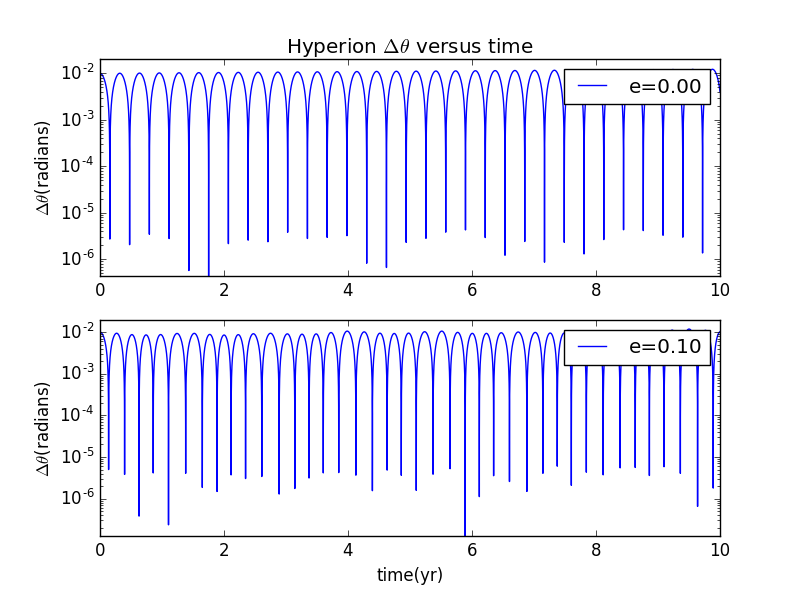
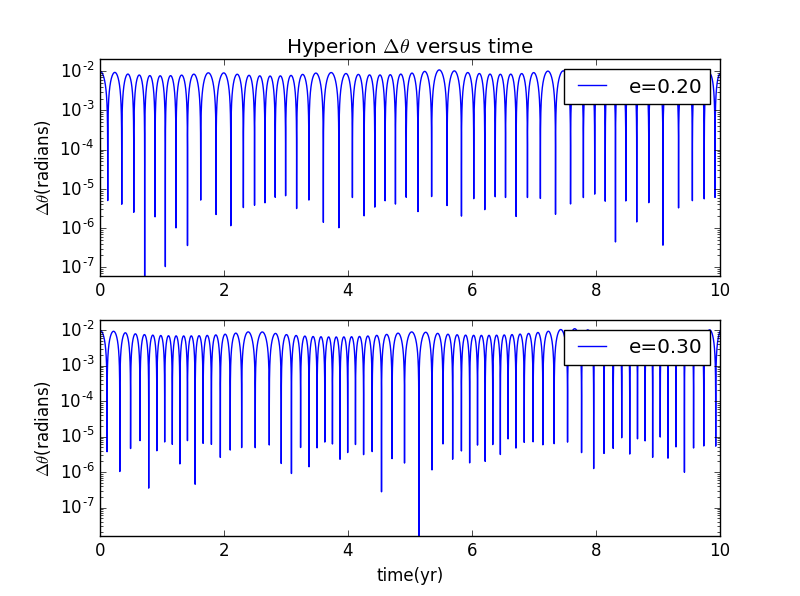
　　3.2 改变$\Delta \theta$的初始值

致谢

Wikipedia--Hyperion