计算物理第六次作业

---

摘要

此次作业为2.10的强化版，引入了迎面风阻，即完成L1。

背景介绍

上次作业中我们通过Euler法完成了对炮弹轨迹的探讨，同时此次探讨偏向理想化探讨，然则在实际问题中我们还要考虑风阻等各种问题，因此此次作业变加强了对实际性问题的研究

正文

1、对于标准情况，即考虑风阻的情况并引入绝热模型分析海拔对风阻影响。
绝热模型公式为：

$$\rho=\rho_0(1-\frac{a y}{T_0})^{\alpha}$$
其中$a=6.5*10^{-3}K/m, \alpha=2.5$,我们很快写出此时的方程如下：
$$\begin{eqnarray*} F^*_{drag}&=&\frac{\rho}{\rho_0}F_{drag}=(1-\frac{ay}{T_0})^{\alpha}\\ v_{x,i+1}&=&v_{x,i}-(1-\frac{ay_{i}}{T_0})^{\alpha}\frac{B_2vv_{x,i}}{m}\Delta t\\ v_{y,i+1}&=&v_{y,i}-g\Delta t-(1-\frac{ay_i}{T_0})^{\alpha}\frac{B_2vv_{x,i}}{m}\Delta t\\ \end{eqnarray*}$$

由此，我们可以写出程序果如下，注：以下为$\theta=45^{\circ}$的情况

import pylab as pl
import math 
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.1,\
                 initial_velocity=700,initial_x=0,initial_y=0,\
                 initial_velocity_x=700*math.cos(math.pi/4),\
                 initial_velocity_y=700*math.sin(math.pi/4)):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.vx = [initial_velocity_x]
        self.vy = [initial_velocity_y]
        self.v = [initial_velocity]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
    def run(self):
        while(1):
            s1=self.x[-1] + self.vx[-1]*self.dt
            s2=self.y[-1] + self.vy[-1]*self.dt
            v1=self.vx[-1] - self.dt *pow((1-(0.0065*self.y[-1])/300),2.5)*\
                           (self.B_2 / self.m) *self.v[-1] * self.vx[-1]
            v2=self.vy[-1] - 9.8*self.dt - self.dt *\
                           pow((1-(0.0065*self.y[-1])/300),2.5)*(self.B_2 / self.m) *\
                           self.v[-1] * self.vx[-1]
            self.x.append(s1)
            self.y.append(s2) 
            self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
            self.vx.append(v1)
            self.vy.append(v2)
            if(s2<0):
                break
    def show_results(self):
        pl.plot(self.x,self.y,'b',label='angle is 45 degree')
        pl.title('Precise guidance system')
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.legend()
        pl.ylim(0,)
        pl.show()
a = cannon()
a.run()
a.show_results()

程序运行结果如图：

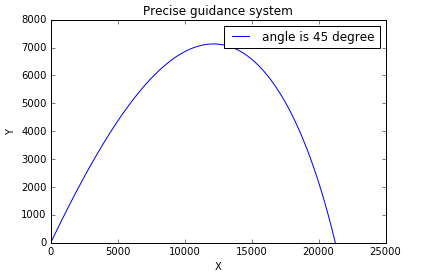
2、考虑迎面风阻，由书上（2.26）可知公式为

$$\frac{B_2}{m}=0.0039+\frac{0.0058}{1+e^{(v-v_d)/\Delta}}$$
其中$v_d=35m/s$,以及$\Delta=5m/s$
由此可知程序应为：

import pylab as pl
import math 
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.1,\
                 initial_velocity=700,initial_x=0,initial_y=0,\
                 initial_velocity_x=700*math.cos(math.pi/4),\
                 initial_velocity_y=700*math.sin(math.pi/4)):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.vx = [initial_velocity_x]
        self.vy = [initial_velocity_y]
        self.v = [initial_velocity]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
    def run(self):
        while(1):
            s1=self.x[-1] + self.vx[-1]*self.dt
            s2=self.y[-1] + self.vy[-1]*self.dt
            v1=self.vx[-1] - self.dt *pow((1-(0.0065*self.y[-1])/300),2.5)*\
                   (0.0039+0.0058/(1+math.exp((self.v[-1]-35)/5)))*\
                   self.v[-1] * self.vx[-1]
            v2=self.vy[-1] - 9.8*self.dt - self.dt *\
               pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
               0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
               self.v[-1] * self.vx[-1]
            self.x.append(s1)
            self.y.append(s2) 
            self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
            self.vx.append(v1)
            self.vy.append(v2)
            if(s2<0):
                break
    def show_results(self):
        pl.plot(self.x,self.y,'b',label='angle is 45 degree')
        pl.title('Precise guidance system')
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.legend()
        pl.ylim(0,)
        pl.show()
a = cannon()
a.run()
a.show_results()

运行结果为：

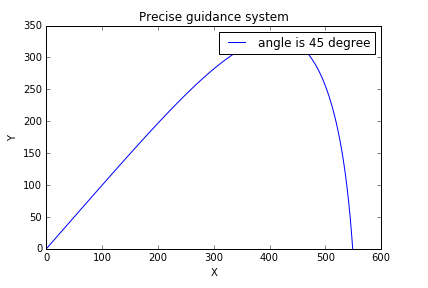
由此对比看出，当考虑迎面风阻的时候，炮弹所打的距离明显减小；
3、考虑目标位置的变化时(初始海拔为100m)，如比原位置更高时候，程序可修改为：

import pylab as pl
import math 
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.01,\
                 total_time=100, initial_velocity=700,initial_x=0,initial_y=100,\
                 initial_angle=45,angle_c=math.pi/180):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.v = [initial_velocity]
        self.vx= [initial_velocity*math.cos(initial_angle*angle_c)]
        self.vy= [initial_velocity*math.sin(initial_angle*angle_c)]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
        self.time = total_time
    def run(self):
         while(1):      
               s1=self.x[-1] + self.vx[-1]*self.dt
               s2=self.y[-1] + self.vy[-1]*self.dt
               v1=self.vx[-1] - self.dt *pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
               v2=self.vy[-1] - 9.8*self.dt - self.dt *\
                           pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
               self.x.append(s1)
               self.y.append(s2) 
               self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
               self.vx.append(v1)
               self.vy.append(v2)
               if(v2<0 and s2<200):
                   s1=self.x[-1] + self.vx[-1]*0.001
                   s2=self.y[-1] + self.vy[-1]*0.001
                   v1=self.vx[-1] - 0.001 *pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
                   v2=self.vy[-1] - 9.8*0.001 - 0.001 *\
                           pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
                   self.x.append(s1)
                   self.y.append(s2) 
                   self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
                   self.vx.append(v1)
                   self.vy.append(v2)
                   if(s2<200):
                       break
                   break
    def show_results(self):
        pl.plot(self.x,self.y,'b',label='45 degree with headwind')
        pl.title('Precise guidance system with higher target')
        pl.ylim(0,600)
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.legend()
        pl.show()
a = cannon()
a.run()
a.show_results()

运行结果为：

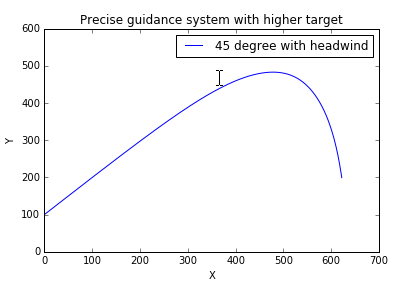
对于较低海拔，程序为：

import pylab as pl
import math 
class cannon :
    def __init__(self,i=0,air_resistance=0.00004,power=10,mass = 1,time_step=0.01,\
                 total_time=100, initial_velocity=700,initial_x=0,initial_y=100,\
                 initial_angle=45,angle_c=math.pi/180):
        self.x = [initial_x] 
        self.y = [initial_y]
        self.v = [initial_velocity]
        self.vx= [initial_velocity*math.cos(initial_angle*angle_c)]
        self.vy= [initial_velocity*math.sin(initial_angle*angle_c)]
        self.t = [0]
        self.m = mass
        self.p = power
        self.B_2 = air_resistance
        self.dt = time_step
        self.time = total_time
    def run(self):
         while(1):      
               s1=self.x[-1] + self.vx[-1]*self.dt
               s2=self.y[-1] + self.vy[-1]*self.dt
               v1=self.vx[-1] - self.dt *pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
               v2=self.vy[-1] - 9.8*self.dt - self.dt *\
                           pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
               self.x.append(s1)
               self.y.append(s2) 
               self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
               self.vx.append(v1)
               self.vy.append(v2)
               if(s2<0):
                   s1=self.x[-1] + self.vx[-1]*0.001
                   s2=self.y[-1] + self.vy[-1]*0.001
                   v1=self.vx[-1] - 0.001 *pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
                   v2=self.vy[-1] - 9.8*0.001 - 0.001 *\
                           pow((1-(0.0065*self.y[-1])/300),2.5)*(0.0039+\
                           0.0058/(1+math.exp((self.v[-1]-35)/5))) *\
                           self.v[-1] * self.vx[-1]
                   self.x.append(s1)
                   self.y.append(s2) 
                   self.v.append(math.sqrt(self.vx[-1]*self.vx[-1] + self.vy[-1]*self.vy[-1]))         
                   self.vx.append(v1)
                   self.vy.append(v2)
                   if(s2<200):
                       break
                   break
    def show_results(self):
        pl.plot(self.x,self.y,'b',label='45 degree with headwind')
        pl.title('Precise guidance system with higher target')
        pl.ylim(0,600)
        pl.xlabel('X')
        pl.ylabel('Y')
        pl.legend()
        pl.show()
a = cannon()
a.run()
a.show_results()

运行结果为：

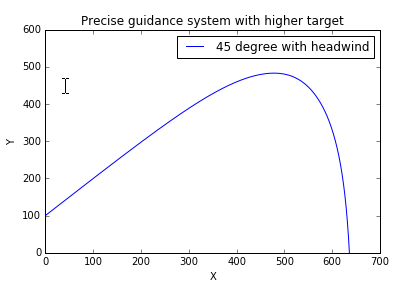
结论

（1）引入迎面风阻后，炮弹的轨迹明显变小，而这其实与初始速度有关，运行不同的初始速度，轨迹也会大不相同；
（2）对于不同高度的目标，炮弹射速和角度也有显然变化。

致谢

感谢宗玥同学的耐心帮助。