张梓桐计算物理第十三次作业

1 Problem

6.12 & 6.16

2 Abstract

In this chapeter we are going to discuss about the behavior of wave,either in ideal model or the relatively real situaion-the piano vibration.While the central ideas in this discussion are applicable to virtually all types of waves on a string.

3 Background

3.1 Wave

In physics, a wave is an oscillation accompanied by a transfer of energy that travels through a medium (space or mass). Frequency refers to the addition of time. Wave motion transfers energy from one point to another, which displace particles of the transmission medium–that is, with little or no associated mass transport. Waves consist, instead, of oscillations or vibrations (of a physical quantity), around almost fixed locations.--Wikipedia,the free encylopeida.

The central equation of wave motion is:

$$\begin{eqnarray*} \frac{\partial^2y}{\partial t^2}&=&c^2\frac{\partial^2y}{\partial x^2} \end{eqnarray*}$$

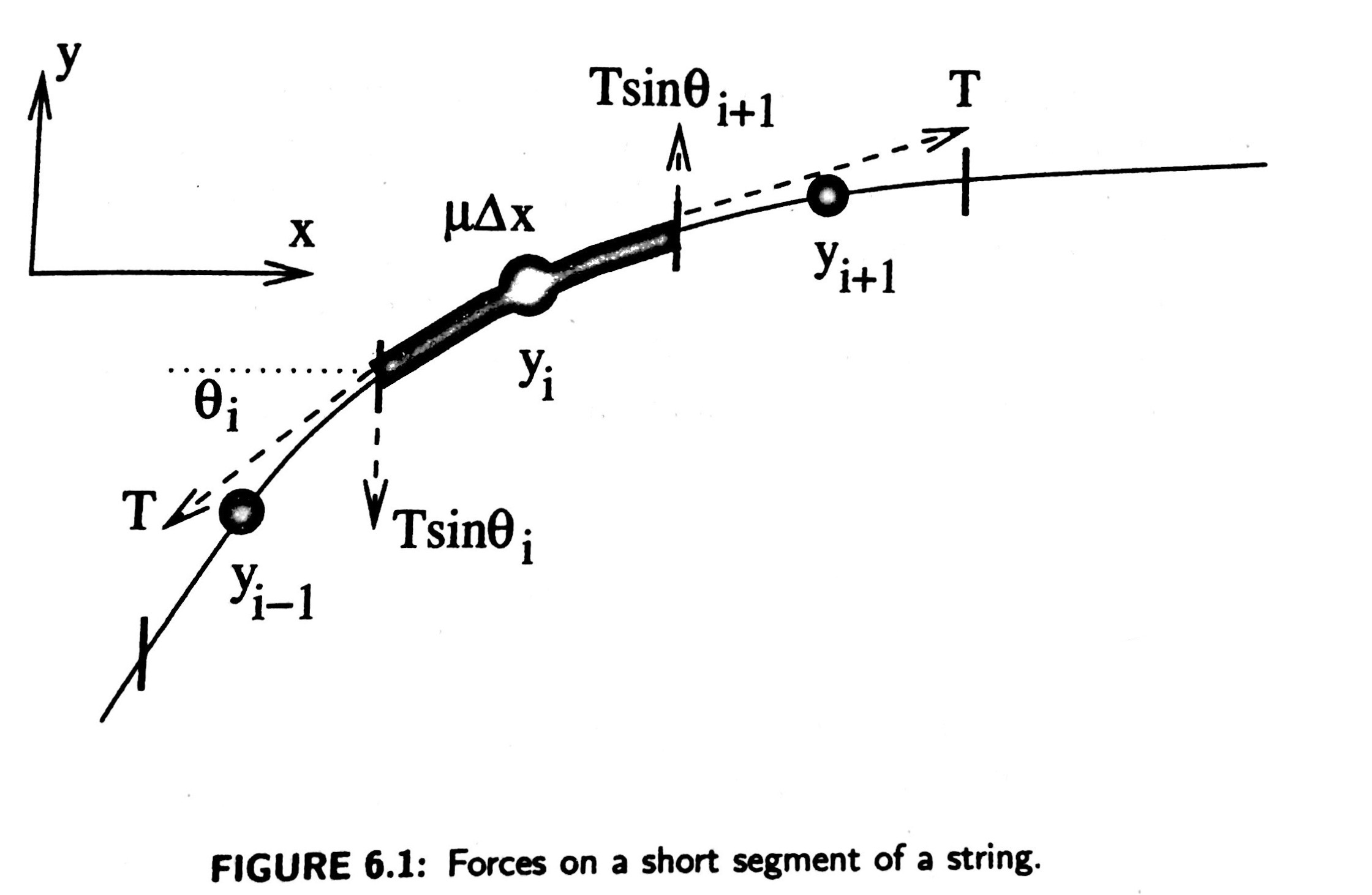
From this picture we can derive the above equation by imposing that:
$$\begin{eqnarray*} (\mu\Delta x)\frac{\partial^2y_i}{\partial t^2}&=Tsin\theta_{i+1}-Tsin\theta_{i} \end{eqnarray*}$$
Then we use a finite difference approximation for the angles:
$$\begin{eqnarray*} sin\theta_{i}\approx\frac{y_i-y_{i-1}}{\Delta x} \end{eqnarray*}$$
We obtain:
$$\begin{eqnarray*} \frac{\partial^2y_i}{\partial t^2}\approx\frac{T}{\mu}\frac{y_{i+1}-2y_i+y_{i-1}}{(\Delta x ^2)}\approx(\frac{T}{\rho})\frac{\partial^2y}{\partial x^2} \end{eqnarray*}$$
By taking time and x into finite setps $x=i\Delta x$ and $t=n\Delta t$. In the numerical approach, we rewrite the equation into this form:
$$\begin{eqnarray*} \frac{y(i,n+1)+y(i,n-1)-2y(i,n)}{(\Delta t)^2}\approx c^2[\frac{y(i,n+1)+y(i,n-1)-2y(i,n)}{(\Delta x)^2}] \end{eqnarray*}$$

3.2 Standing Waves

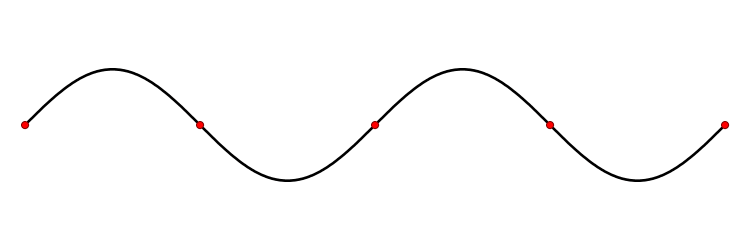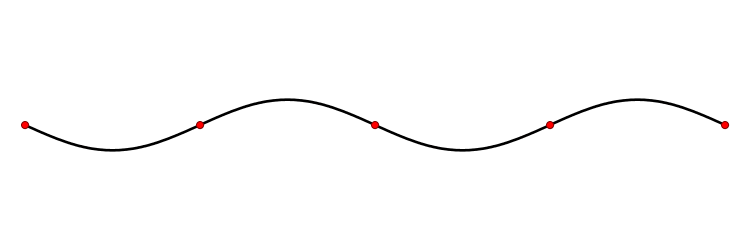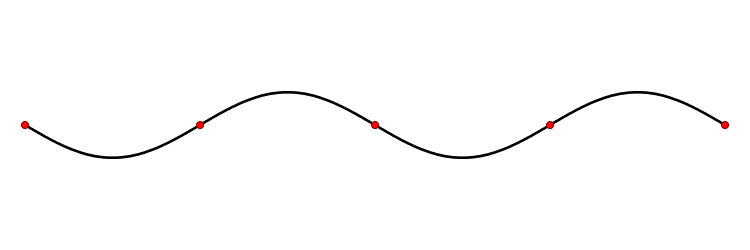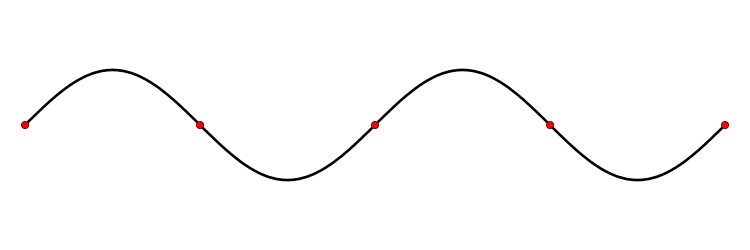
A standing wave, also known as a stationary wave, is a wave that remains in a constant position. This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling in opposite directions.

The figure on the left hand is a two-dimensional standing wave on a disk; this is the fundamental mode.The figure on the right hand is a two nodal lines crossing at the center; this is an overtone.

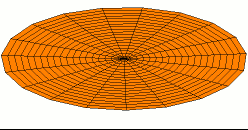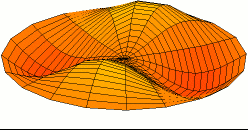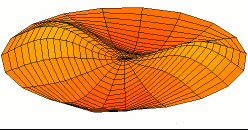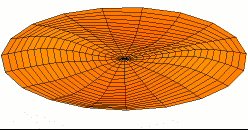
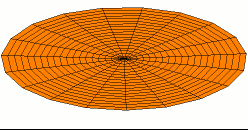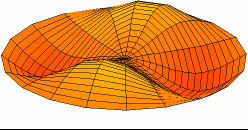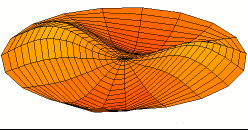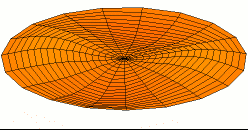
3.3 Wavepacket

In physics, a wave packet (or wave train) is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change (dispersion) while propagating.

Those figure illustrate the dispersion with or without dispersion.

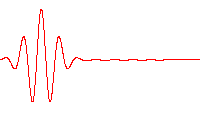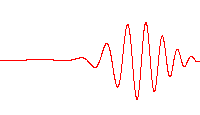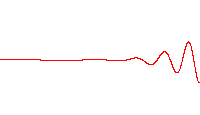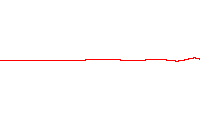
Here in our discussion the Gaussian pluck is usually used:

$$\begin{eqnarray*} y_0(x)=e^{-k(x-x_0)^2} \end{eqnarray*}$$

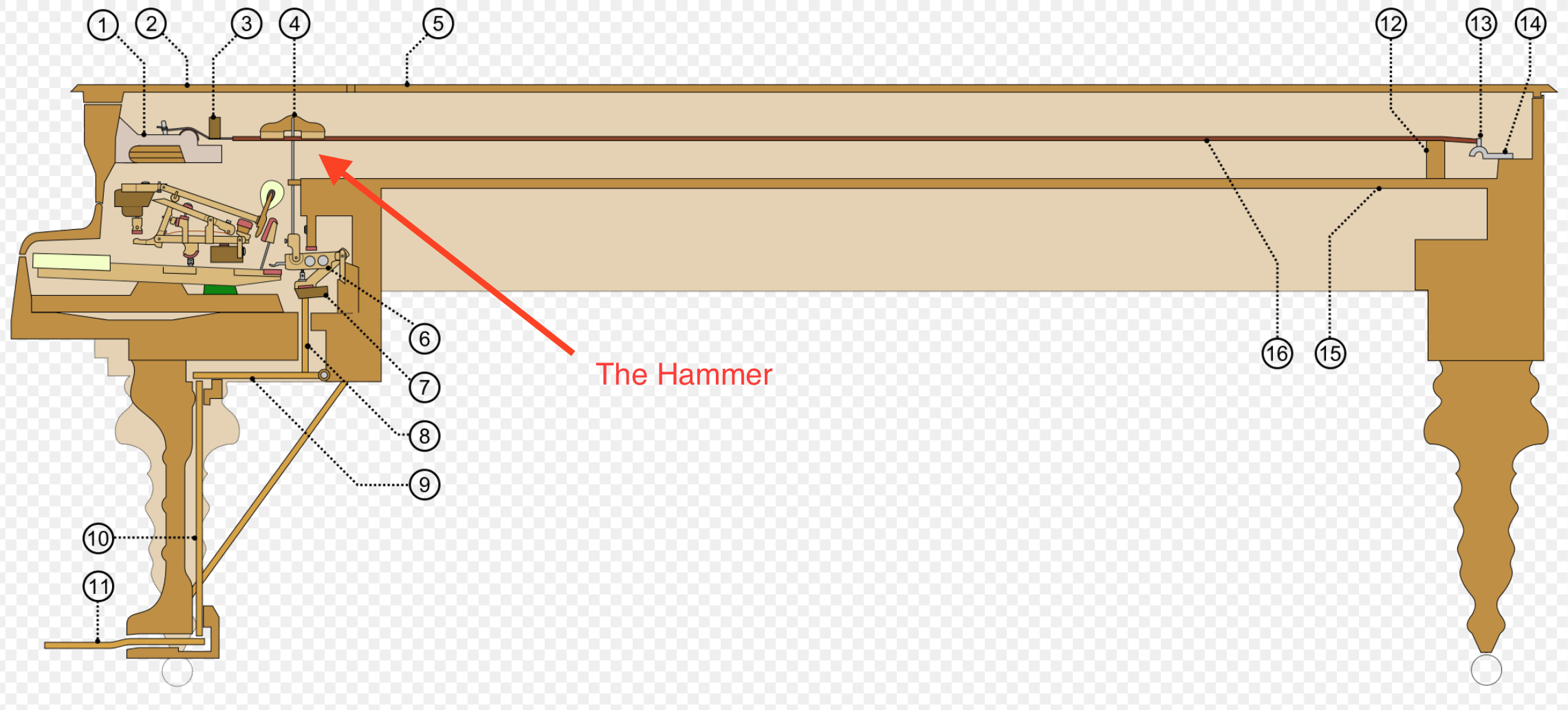
3.4 Structure of The Piano

On the piano string, waves reflect from both ends. The superposition of reflecting waves results in a standing wave pattern, but only for wavelengths $λ = 2L$, $L$, $L/2$, ... = $2L/n$, where L is the length of the string. Therefore, the only frequencies produced on a single string are $f = nv/(2L)$. Timbre is largely determined by the content of these harmonics. Different instruments have different harmonic content for the same pitch. A real string vibrates at harmonics that are not perfect multiples of the fundamental.

4 Main Body

Source Code

5 Results

5.1 Different Gaussian Wavepackets with fixed ends.

Gaussian equations are chosen as the initial condition, that is, $y(i,n=0)$. From the equation above $y(i,n=-1)$ is needed. Here we assume that the string before the instant the program begins has the same initial condition.That is to say $y(i,n=-1)=y(i,n=0)$

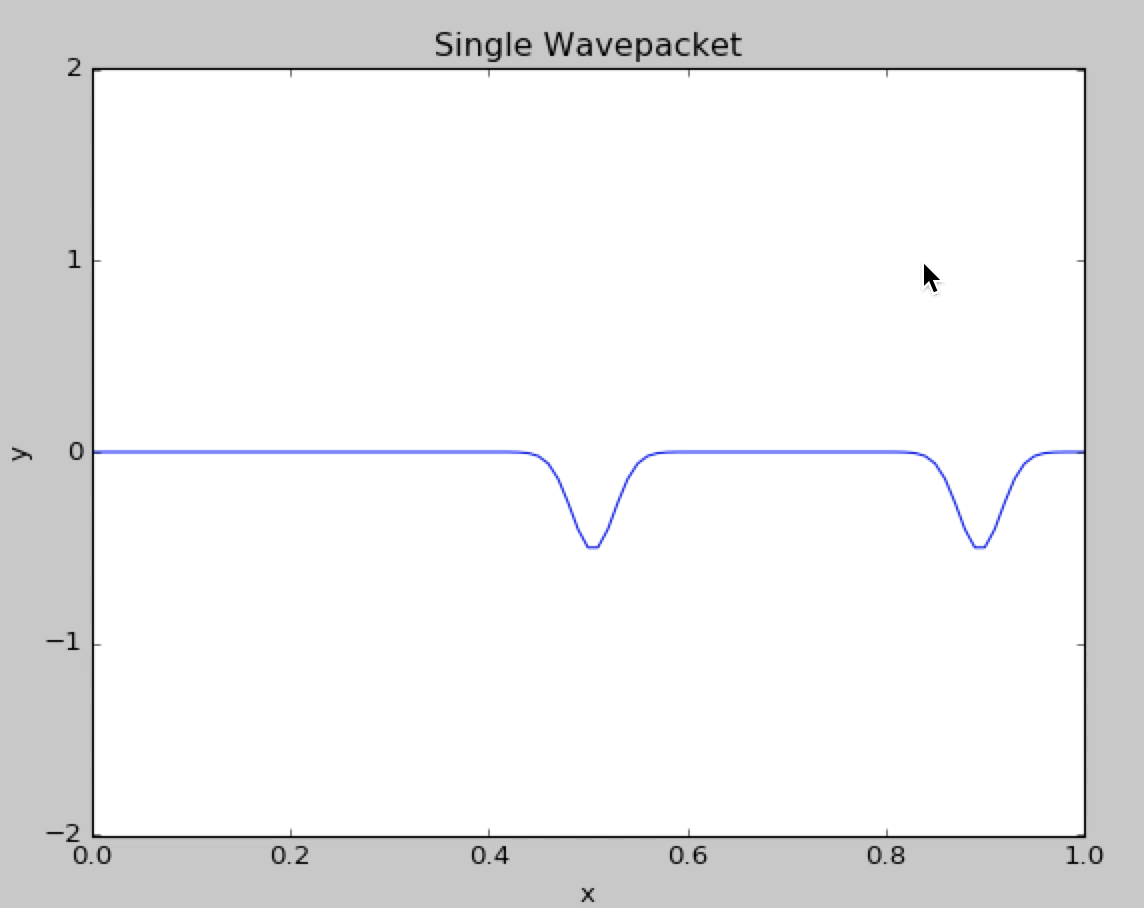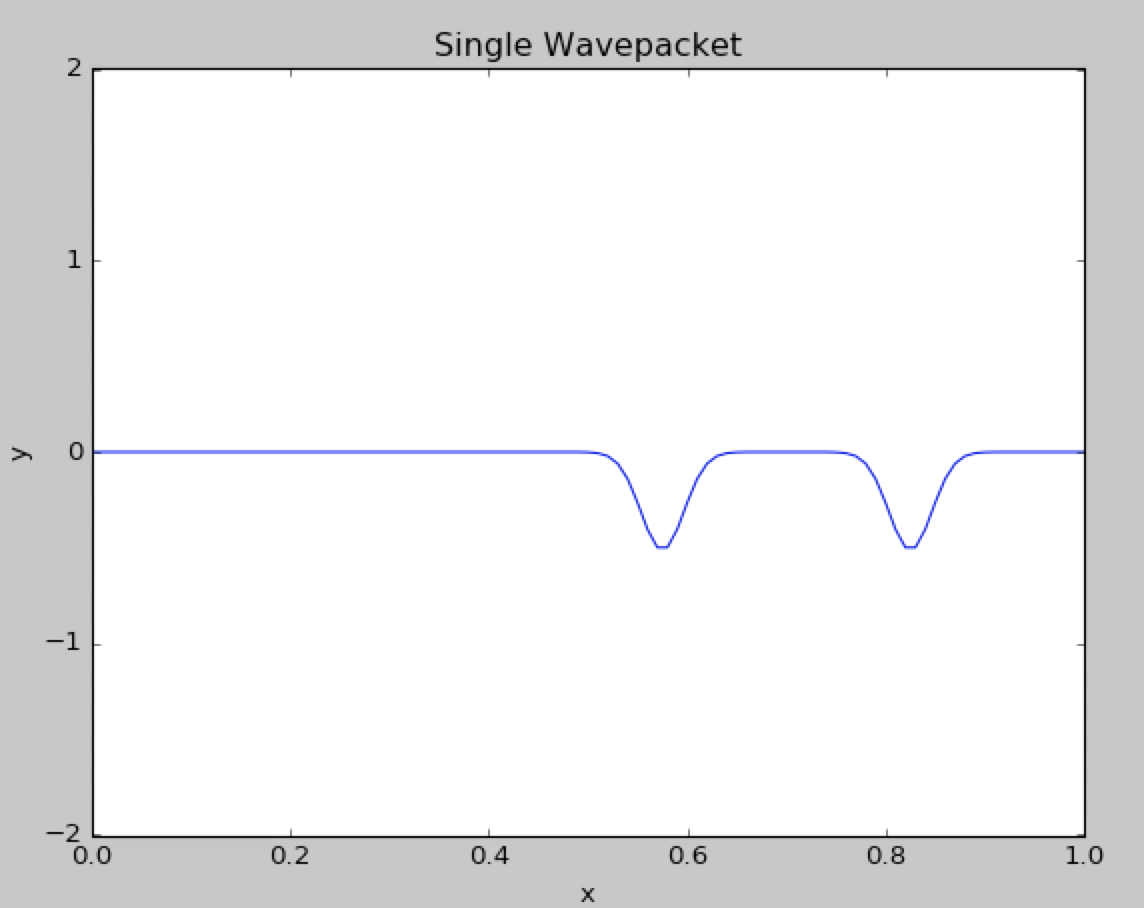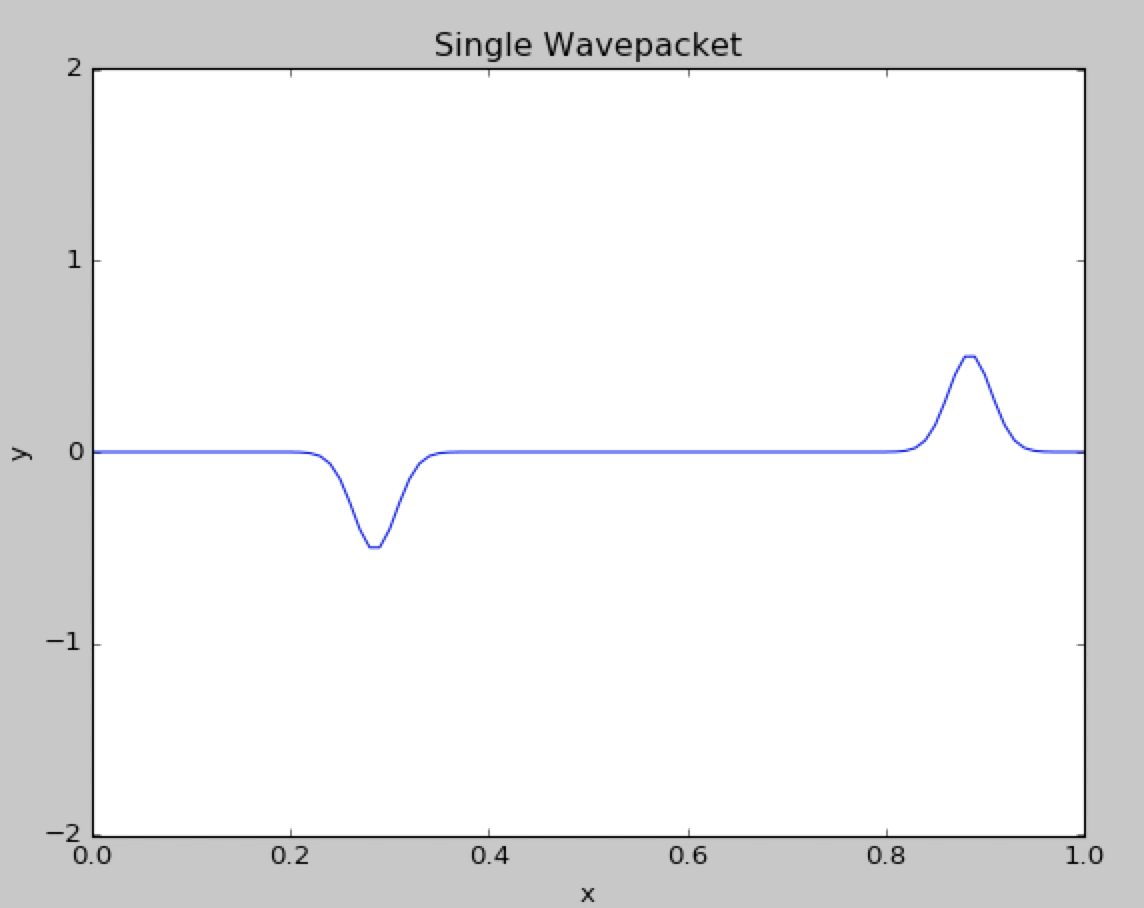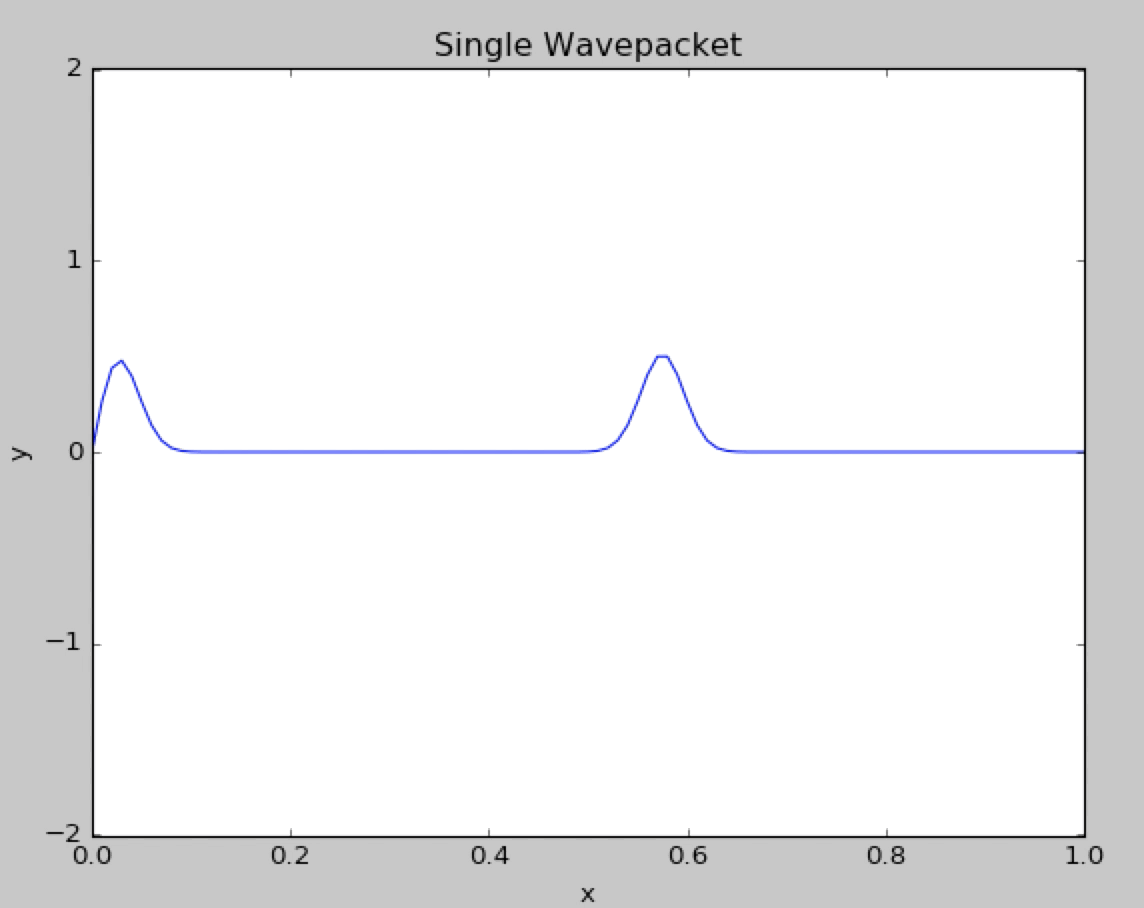
In the program we used the fixed boundary condition :

$$\begin{eqnarray*} y(0,n)=y(M,n)=0 \end{eqnarray*}$$
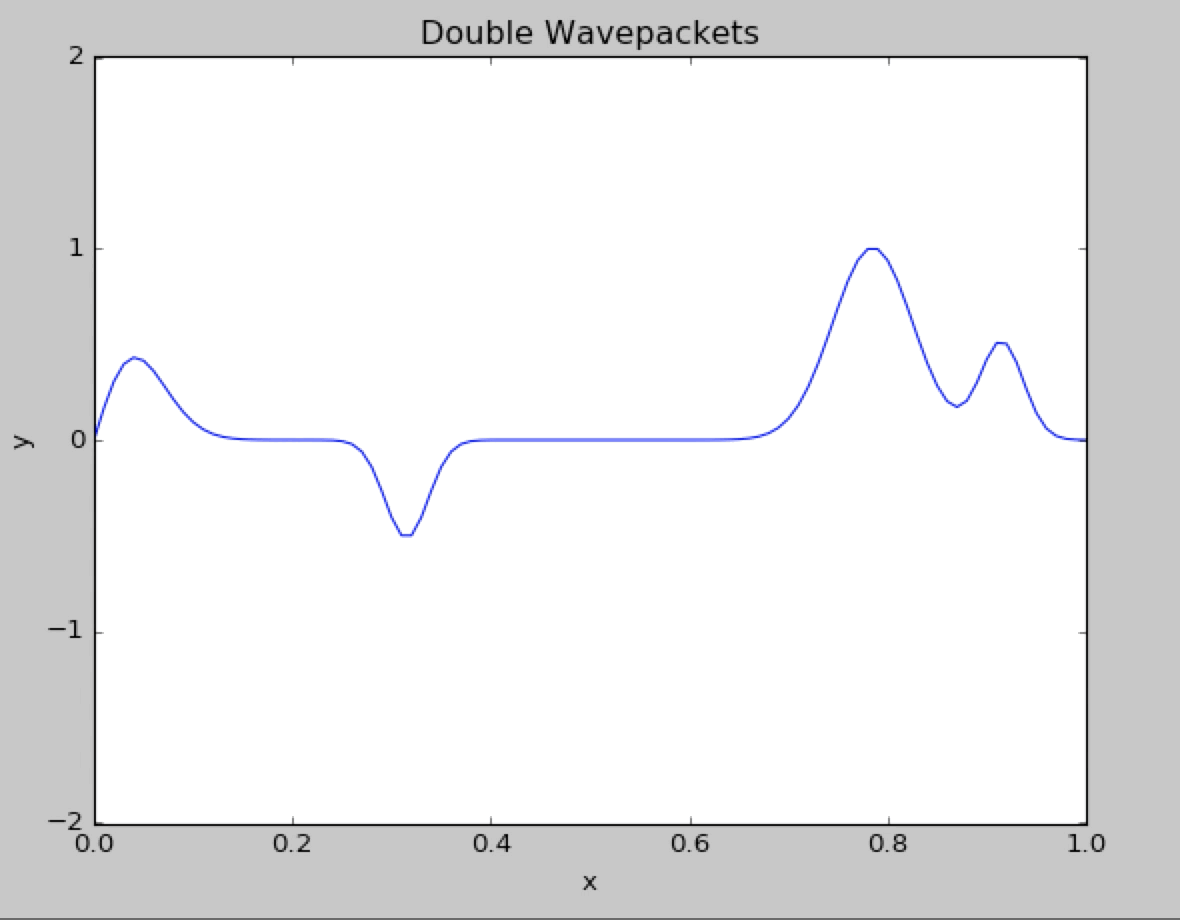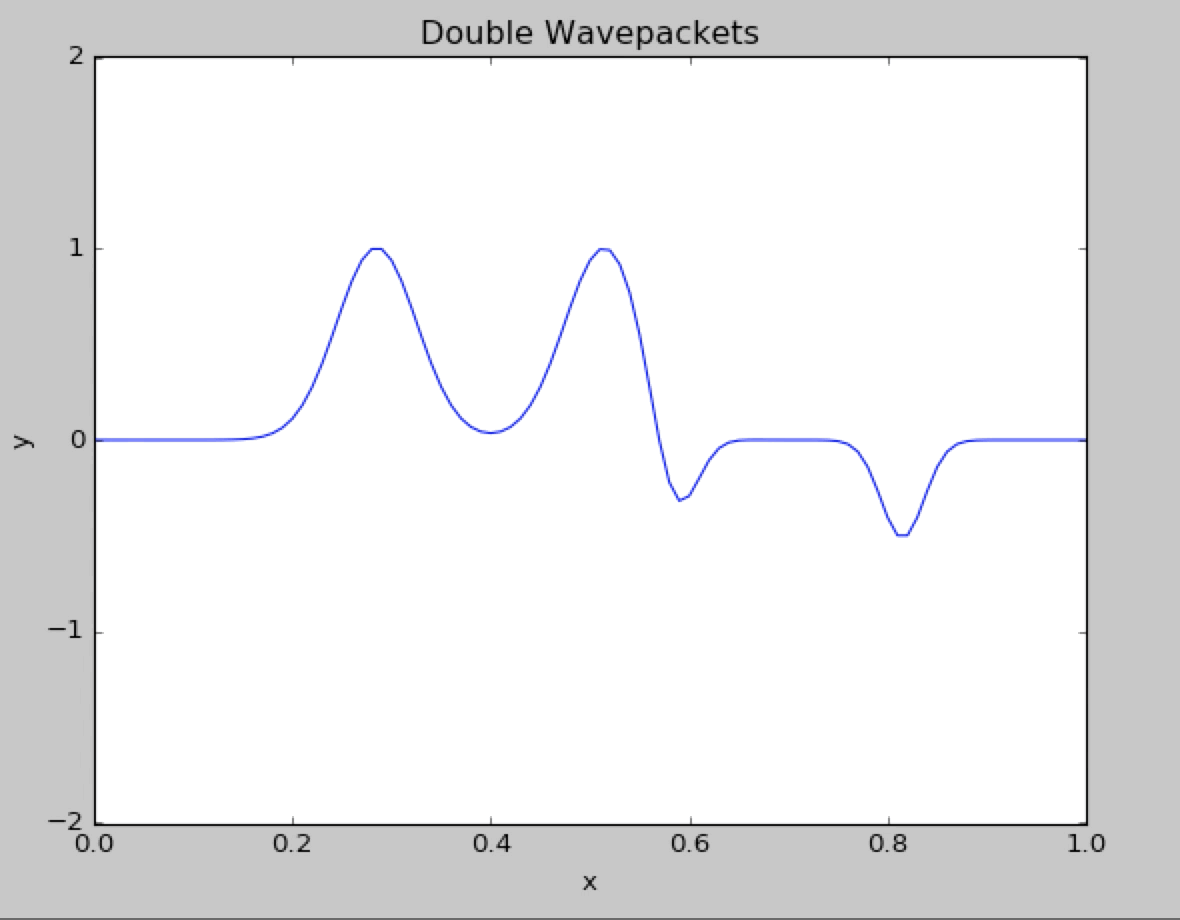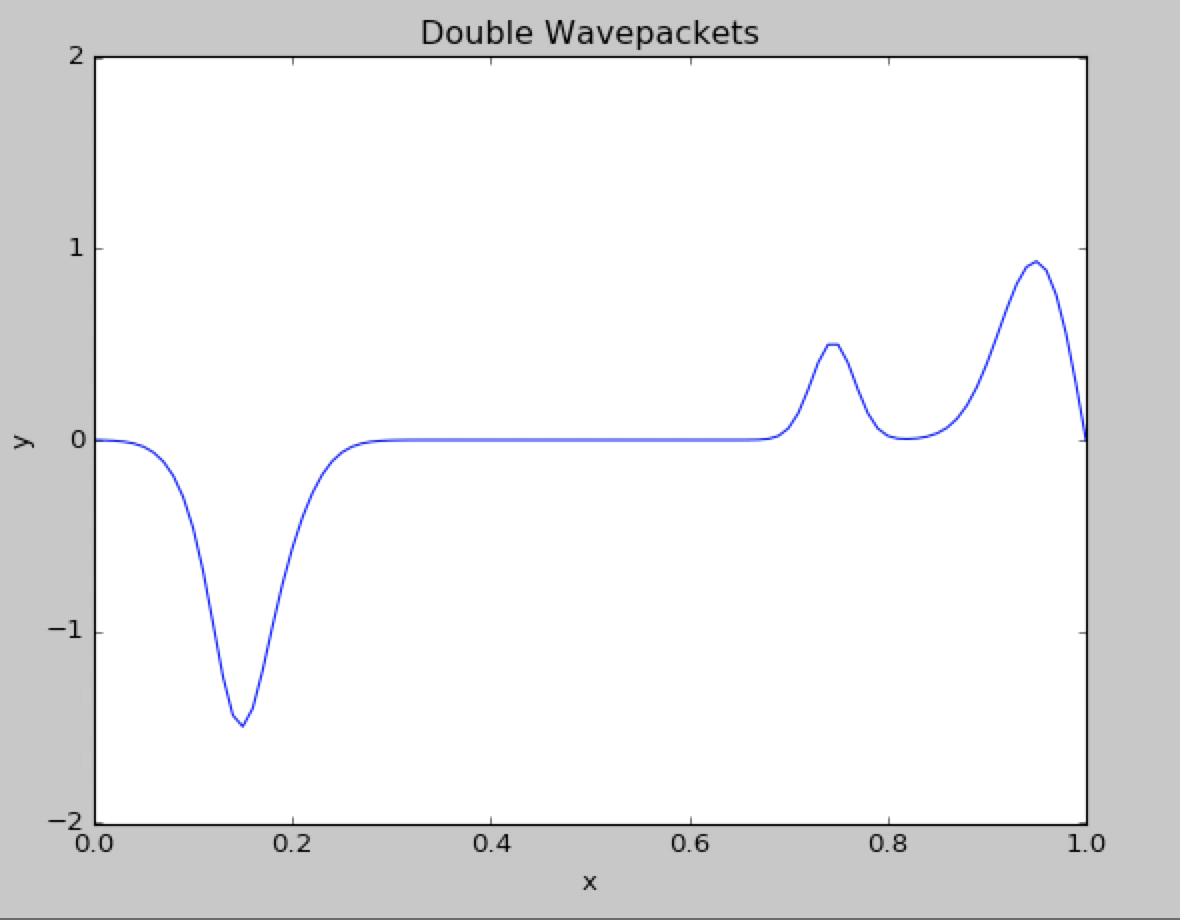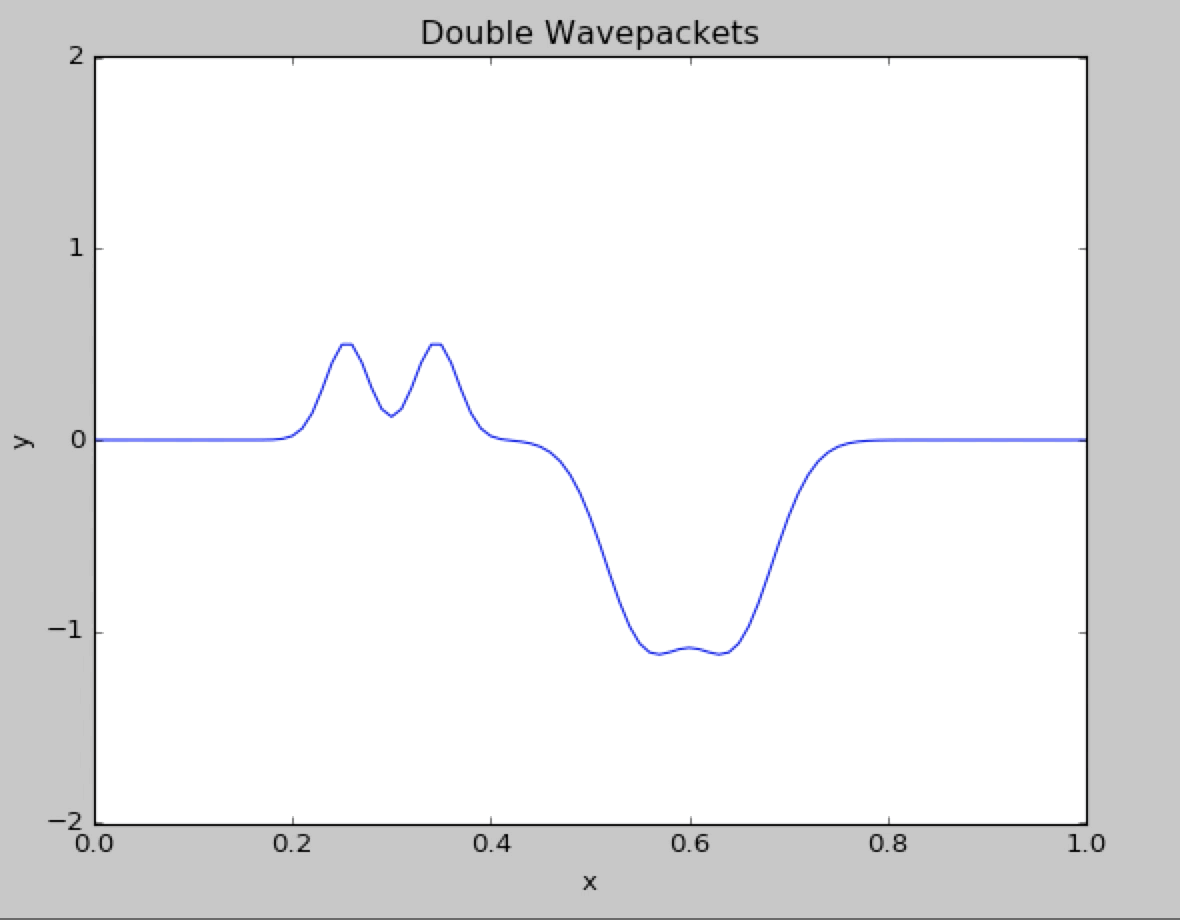
Here is a figure describing the two wavepacket came across each other, We can see that two wavepackets pass through

each other without changing shape or speed.

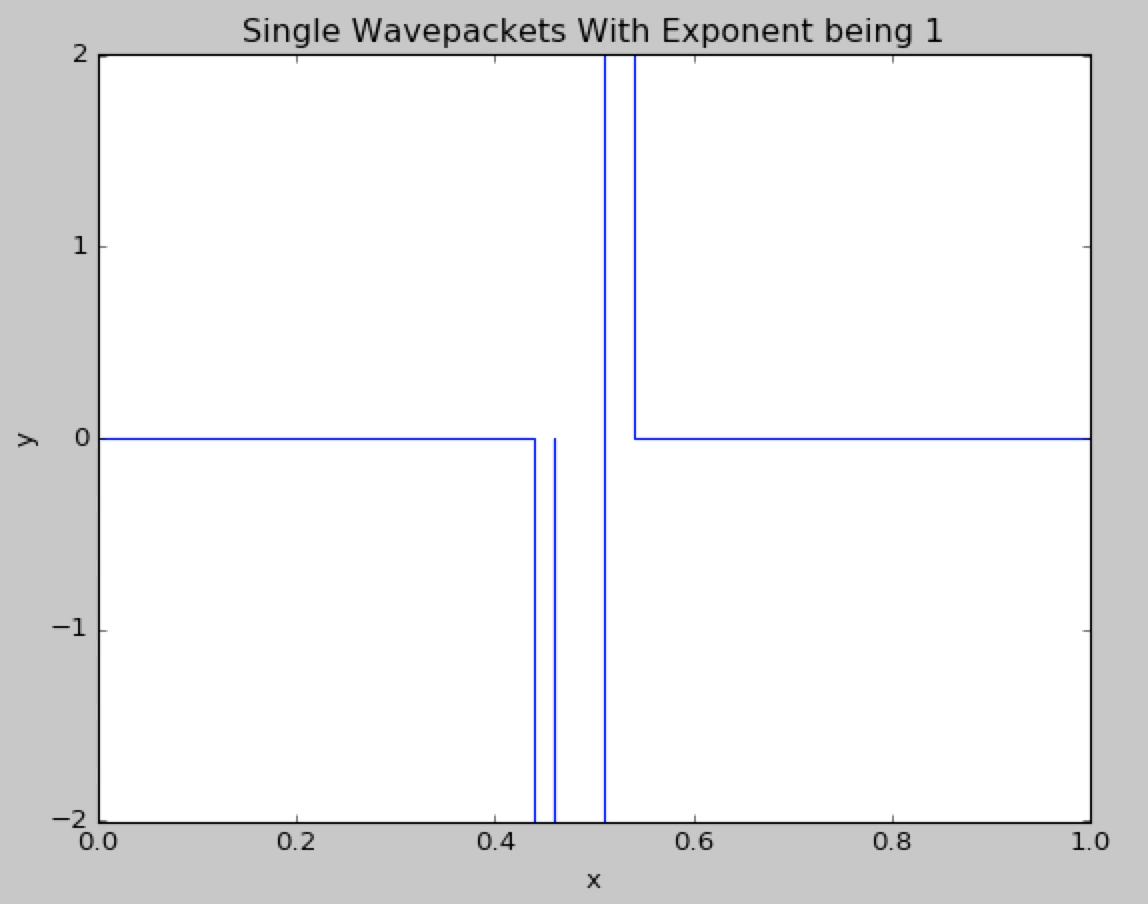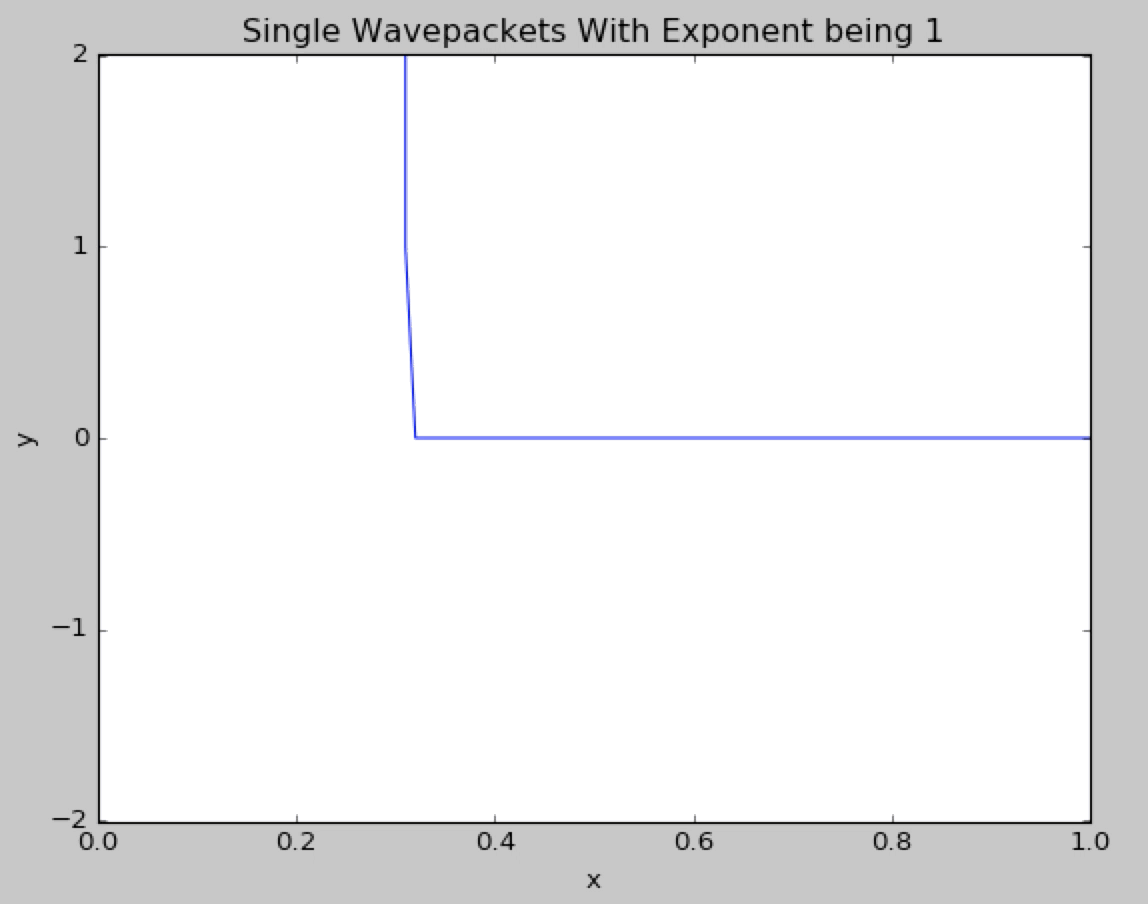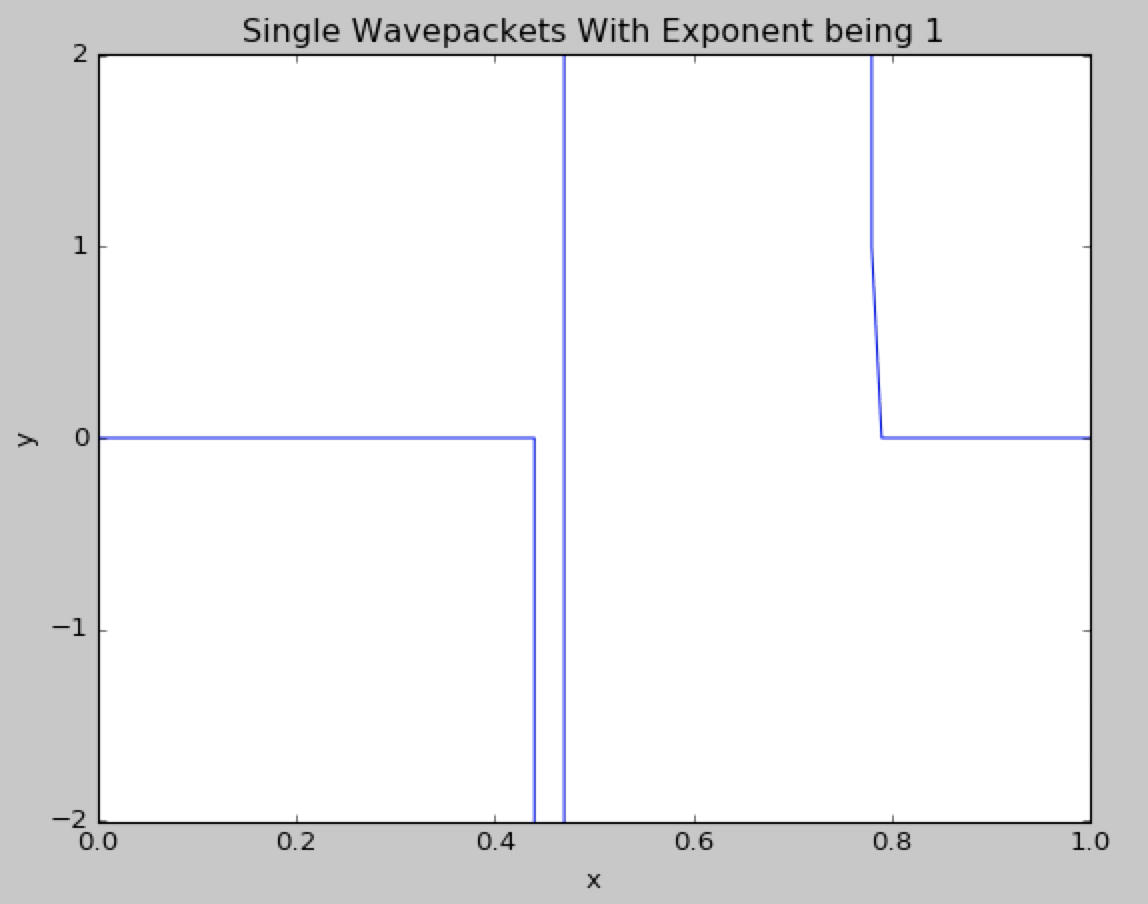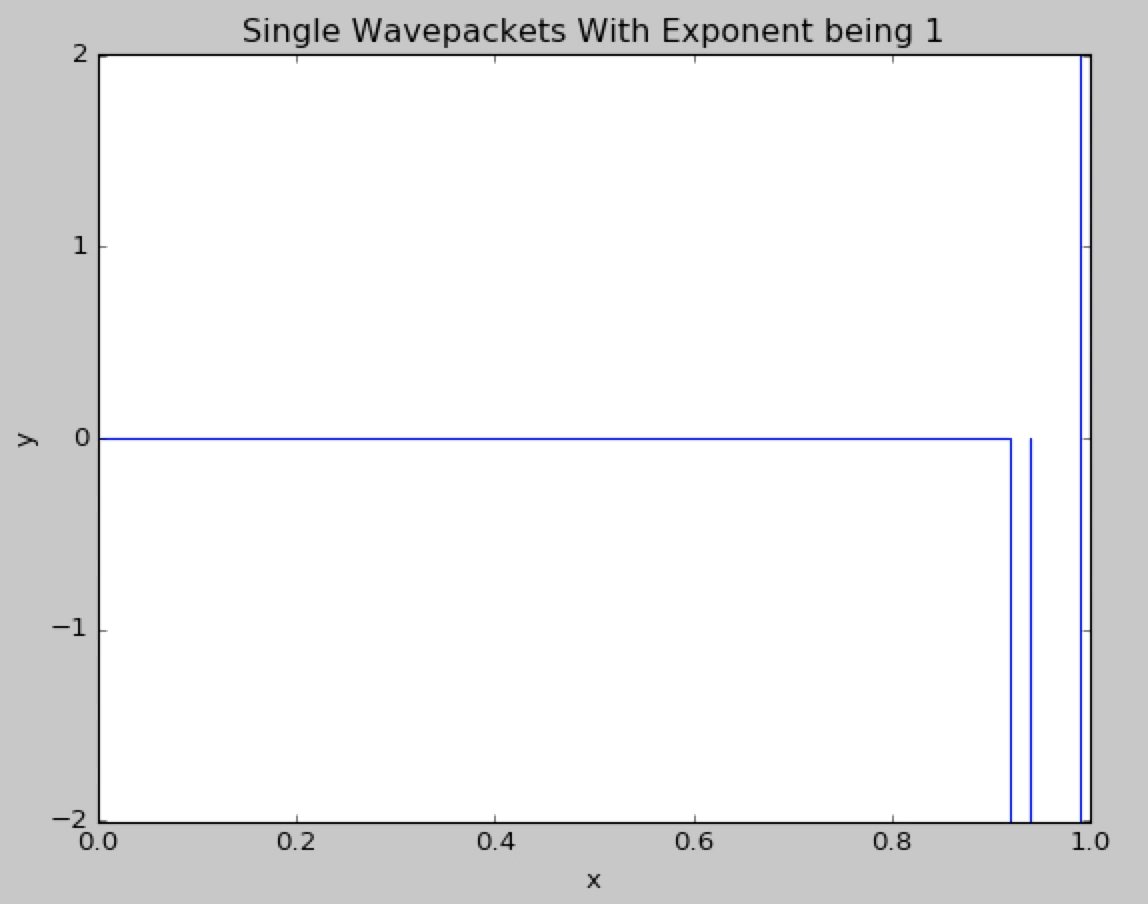
Now we change the gaussian exponent from 2 to 1.We can observe the highly unstable behavior of the wave packet.The shape of the wavepacket is resembing the square wave.

Now we change the gaussian exponent from 2 to 3.We can see in details that the wavepacket diverge.

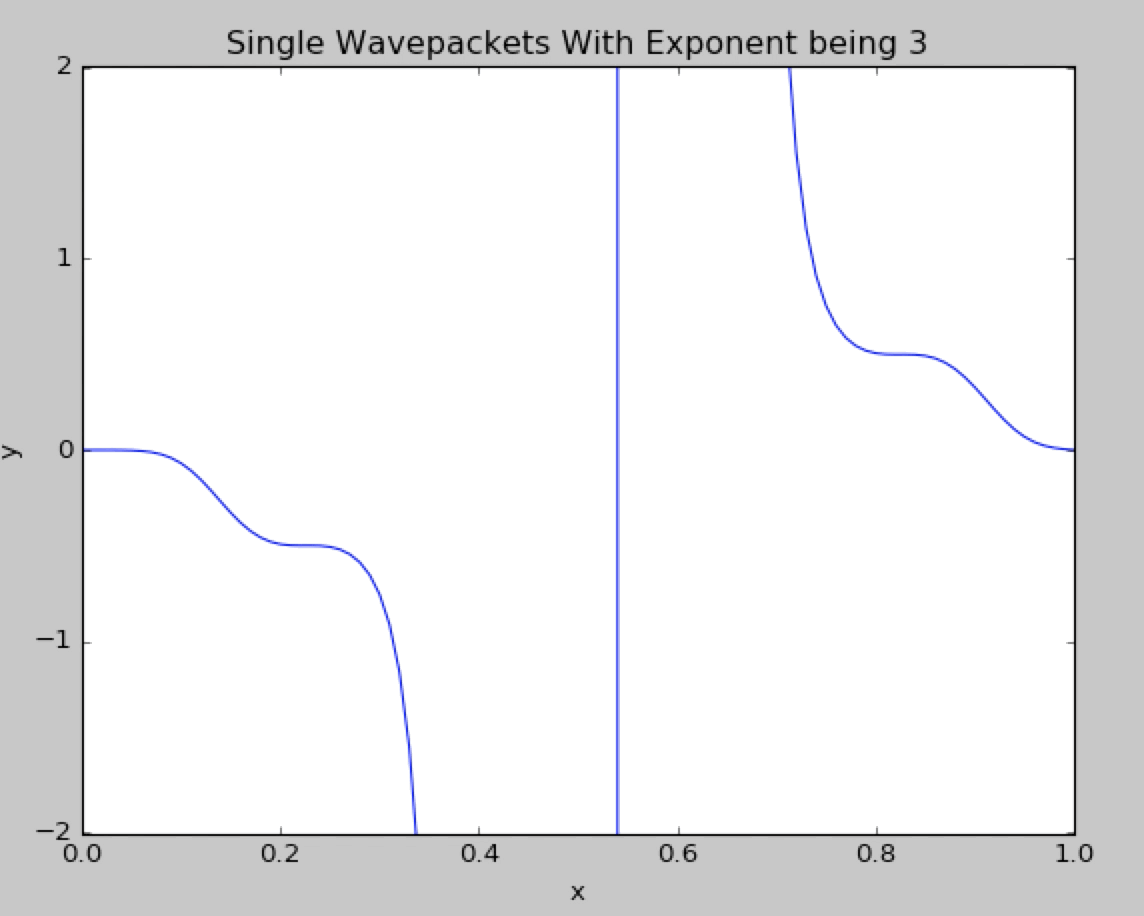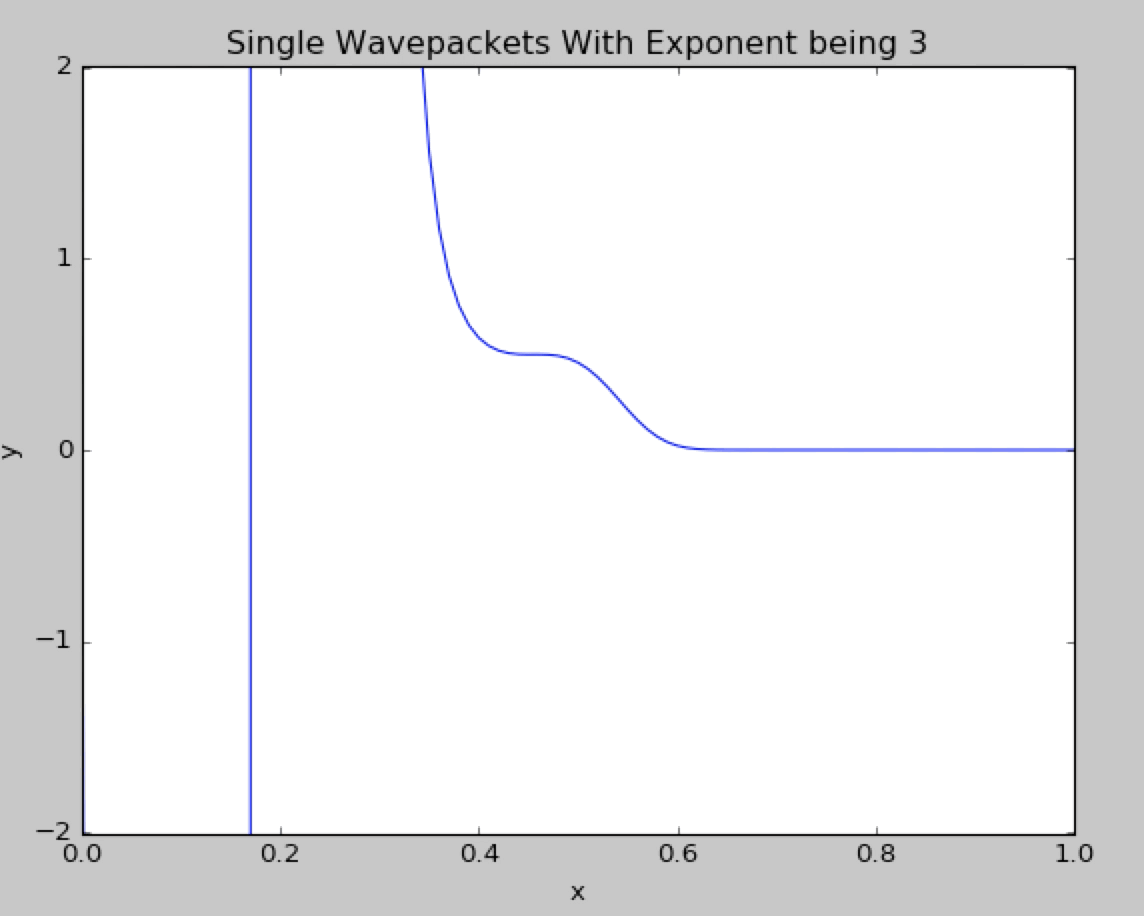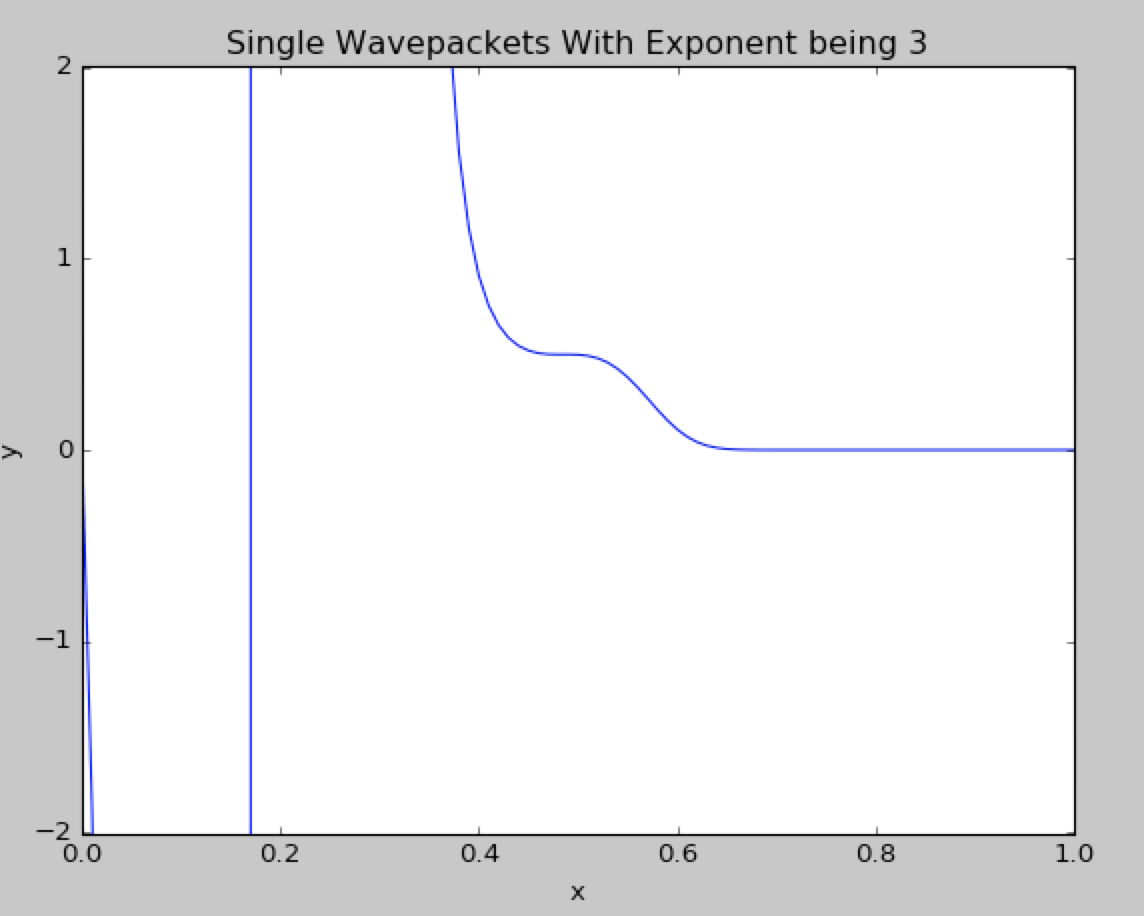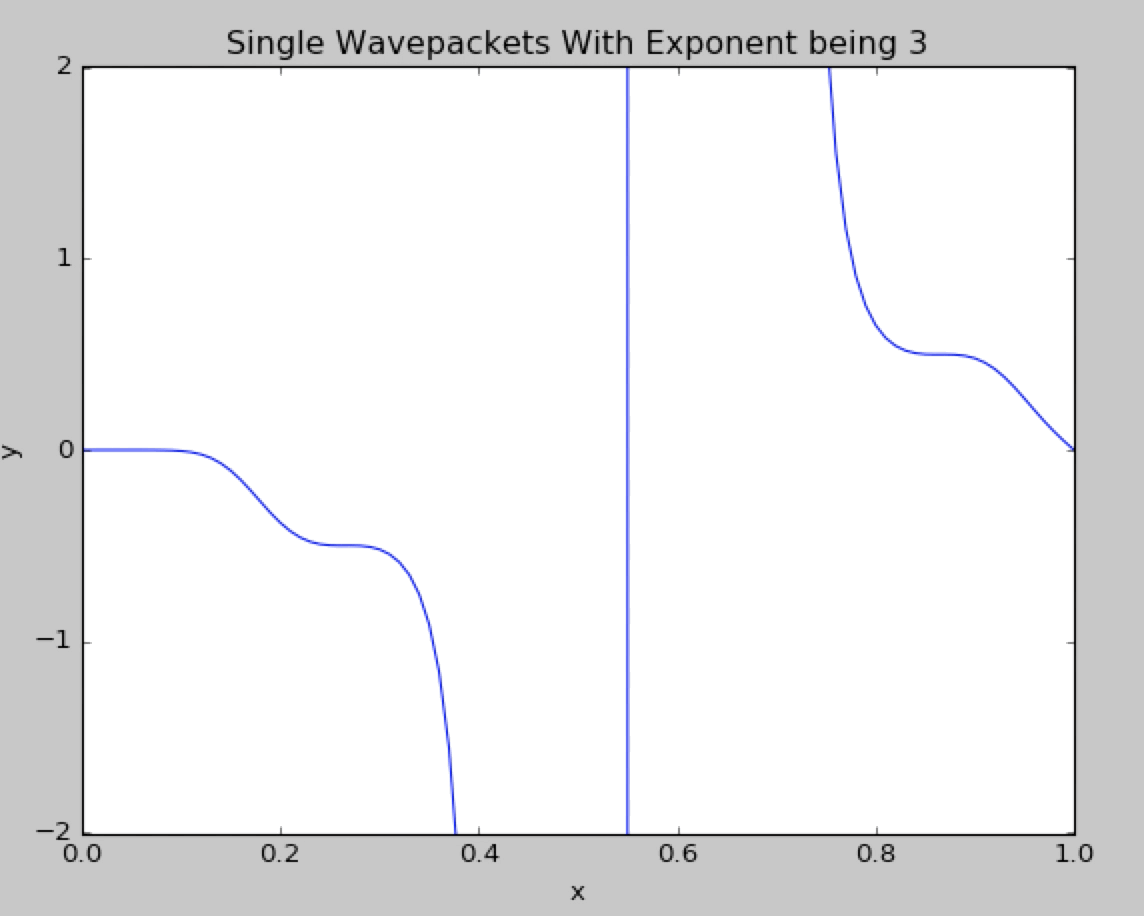
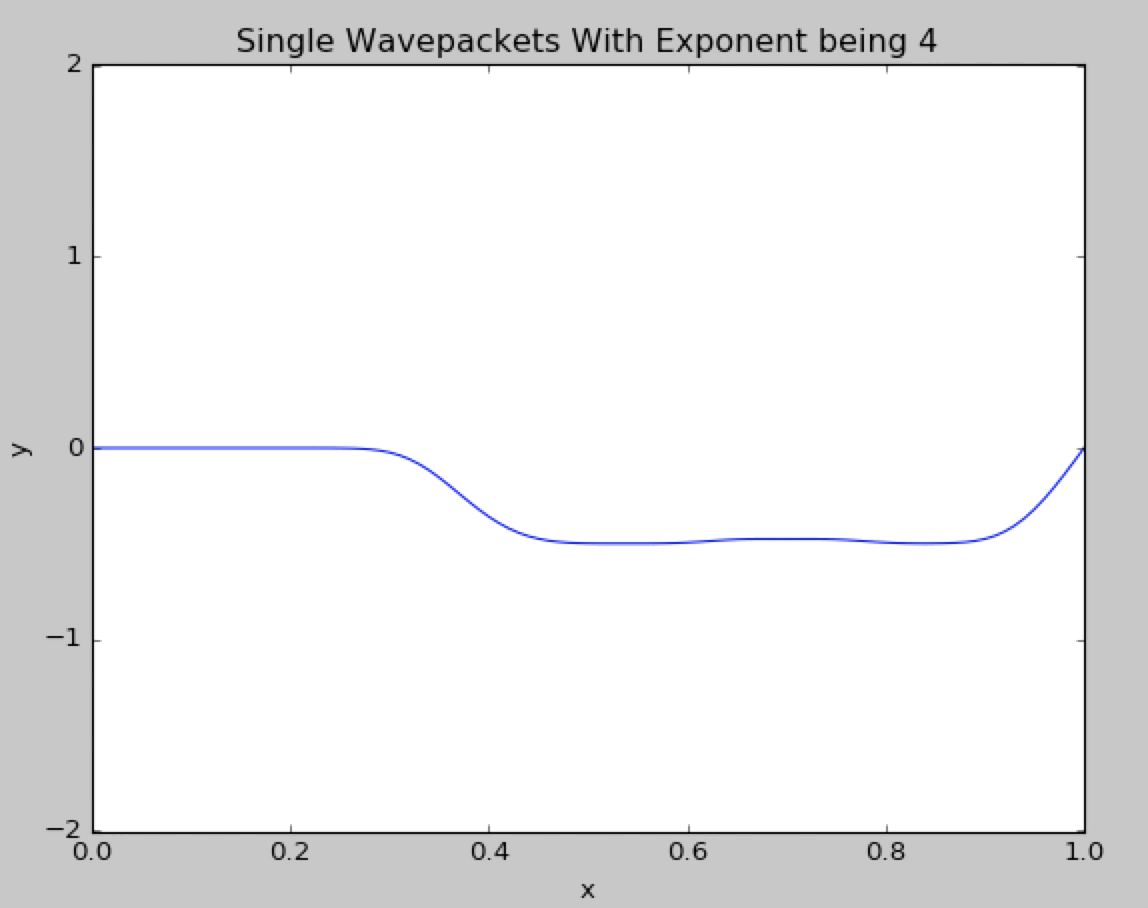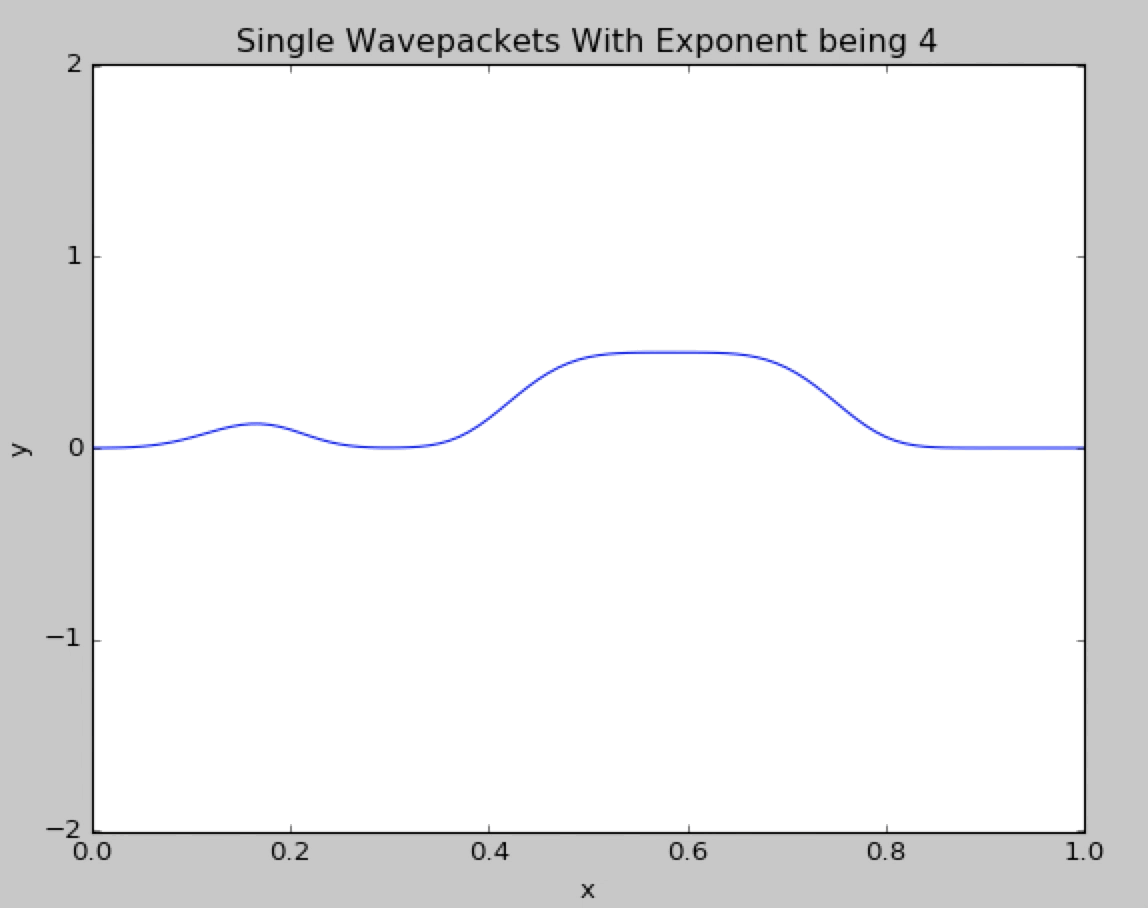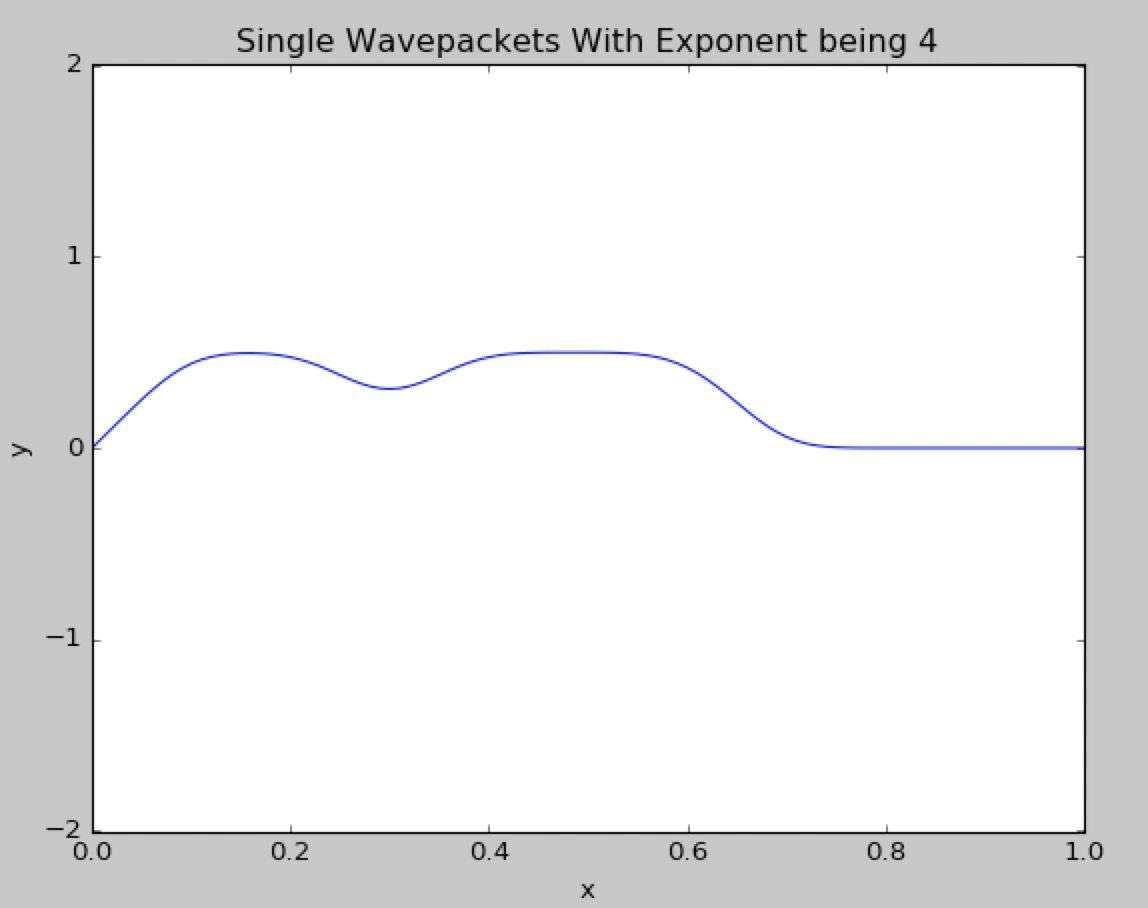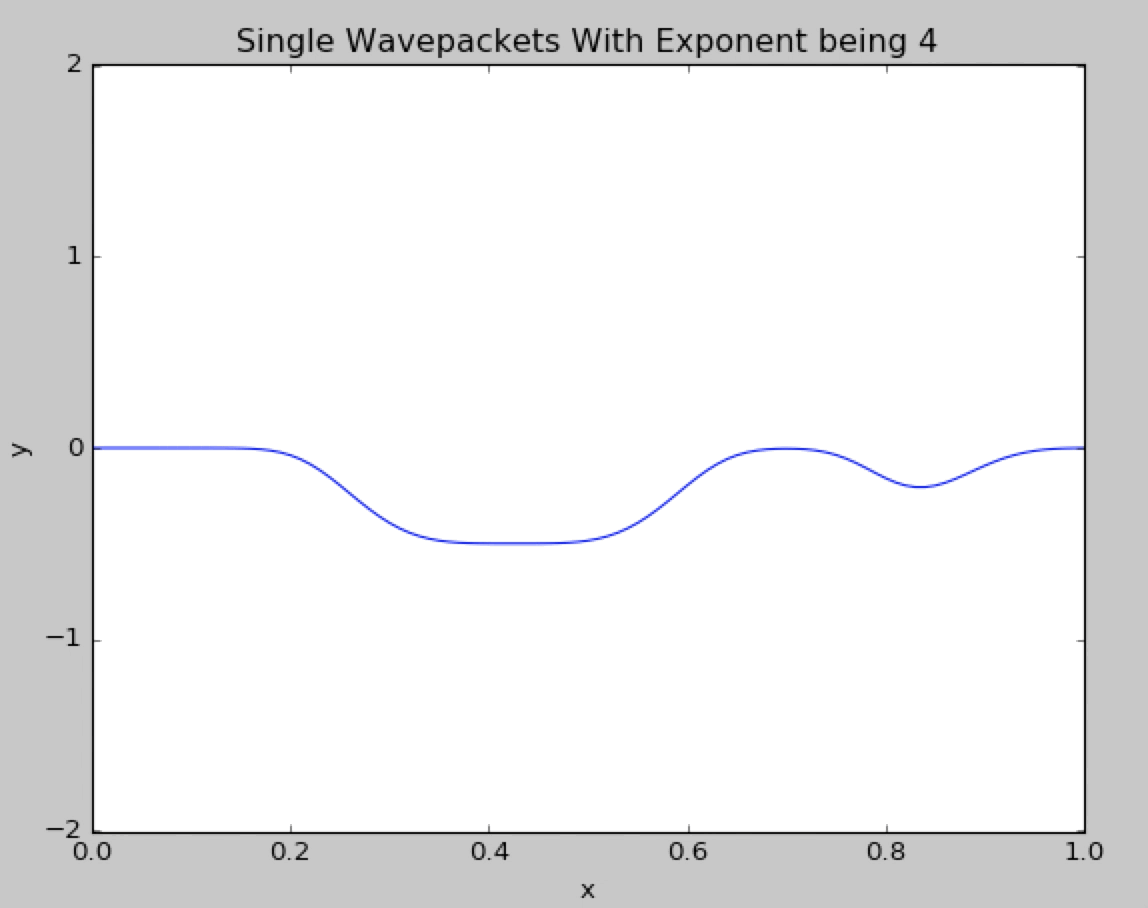
What if we change the gaussian exponent from 2 to 4.The wavepacket behaves like the normal gaussian exponent and no divergence is observed.

Here is the usual Sine wavepacket.

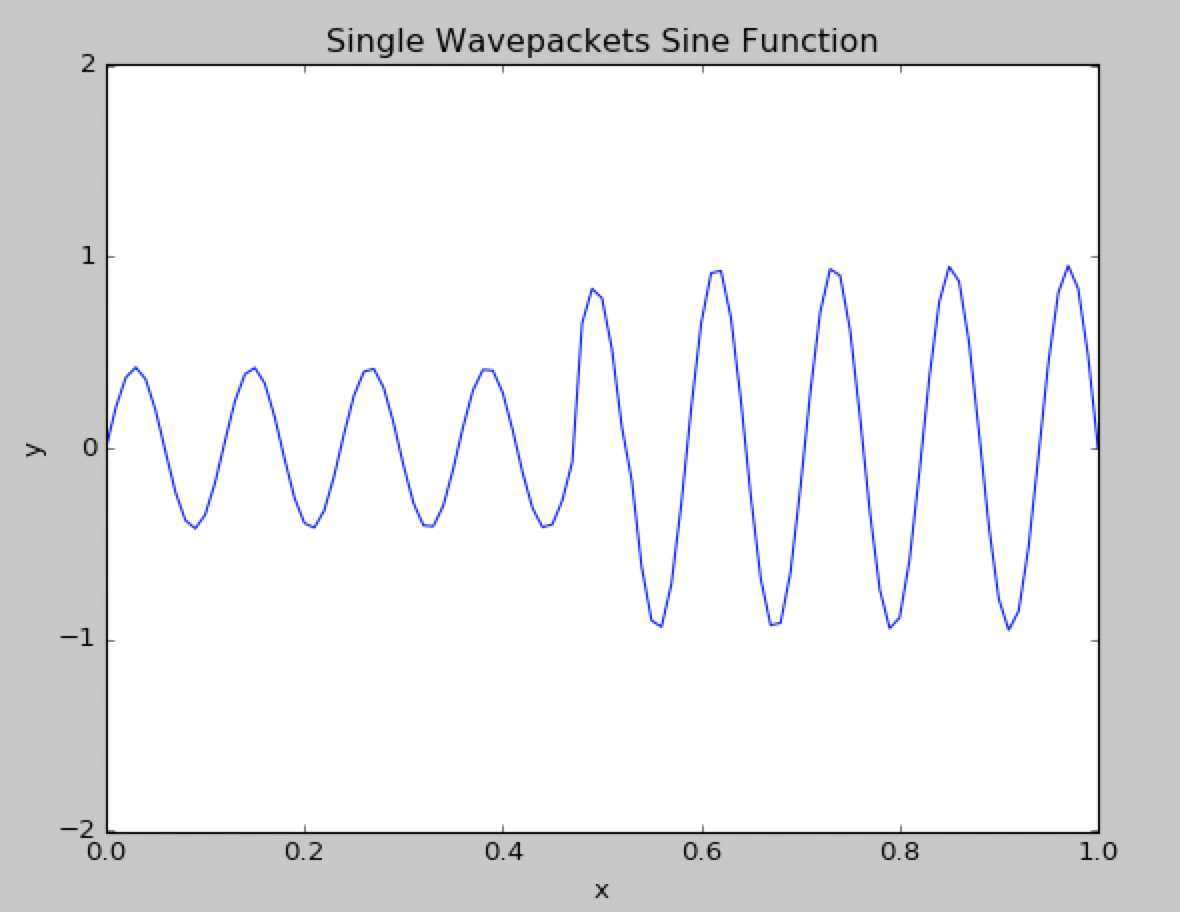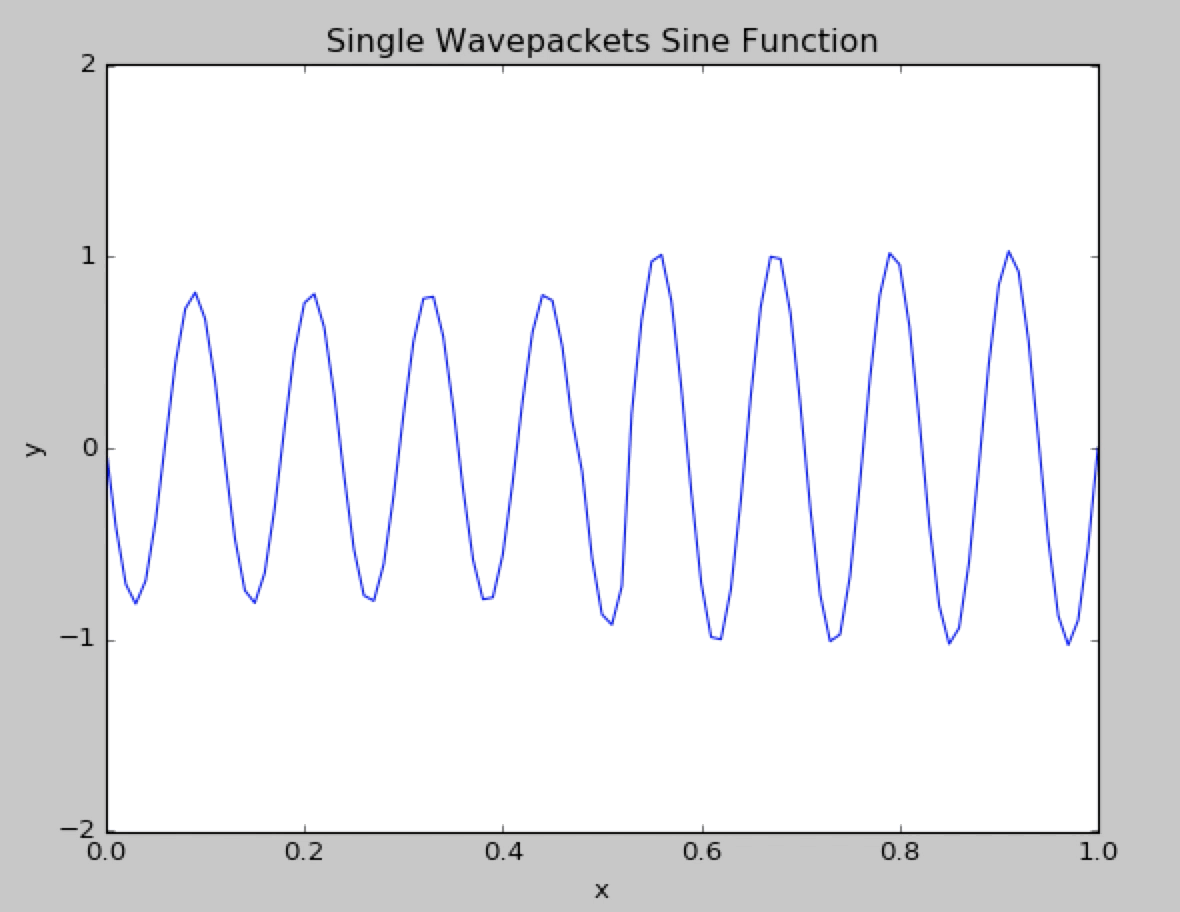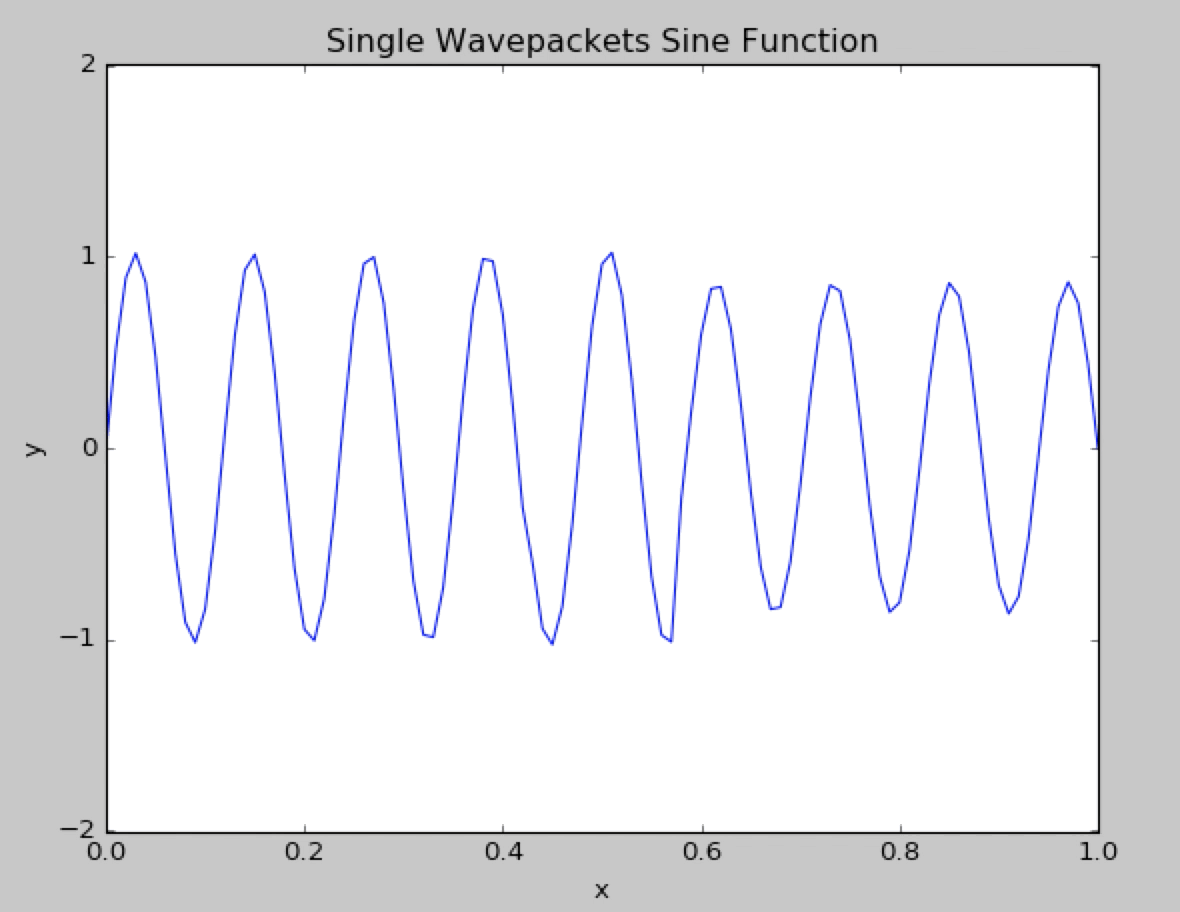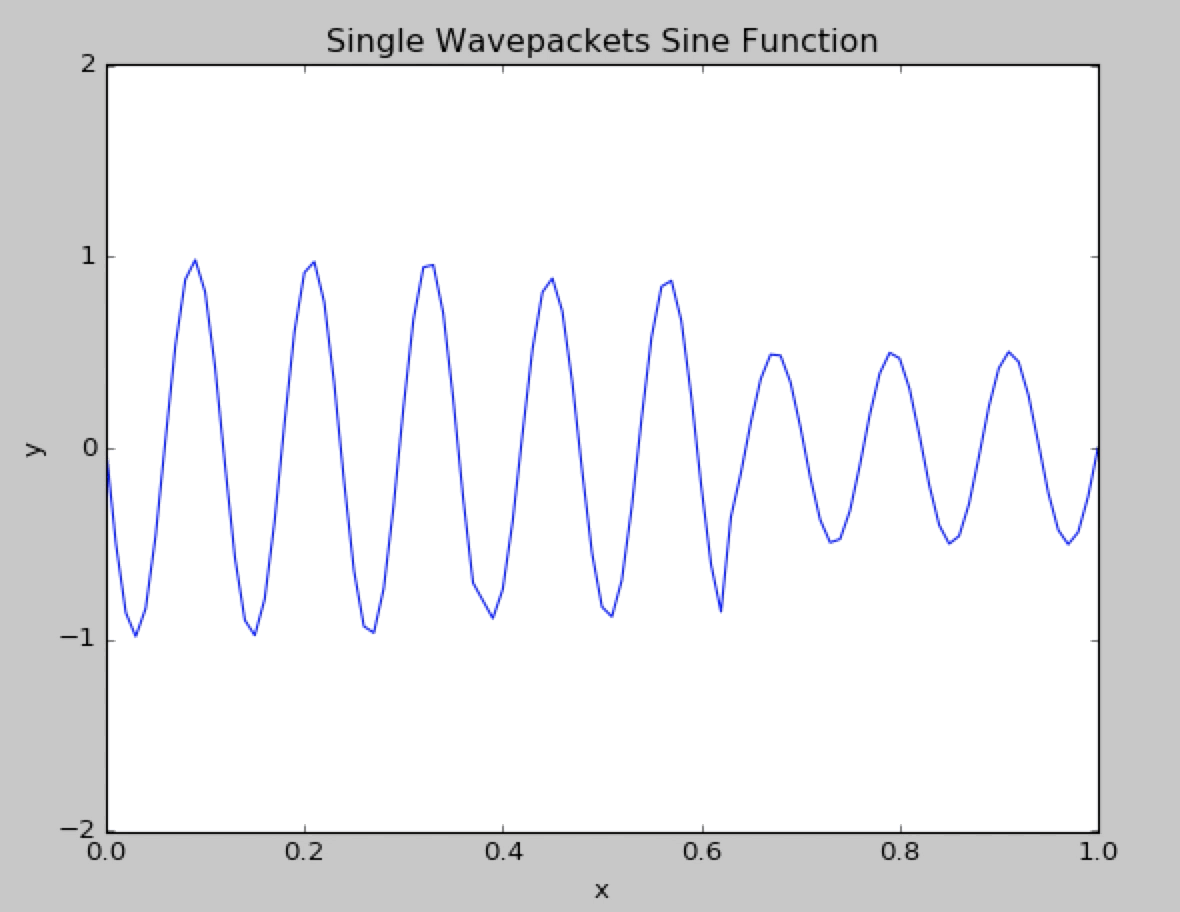
5.2 Results With Spectrum and Signal

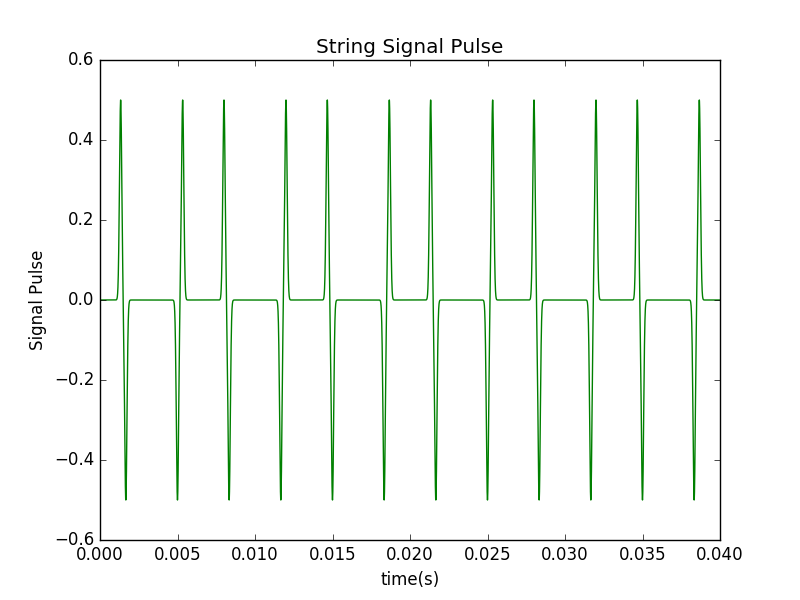
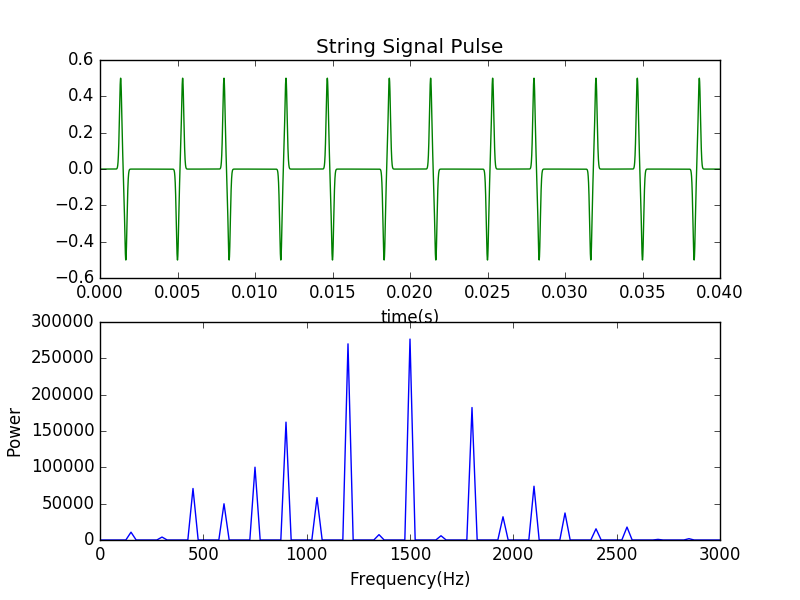
Here are the figure that illustrate the signal of the point at x=0.05.The string was excited with a Gaussian initial pluck centered at the middle of the string.

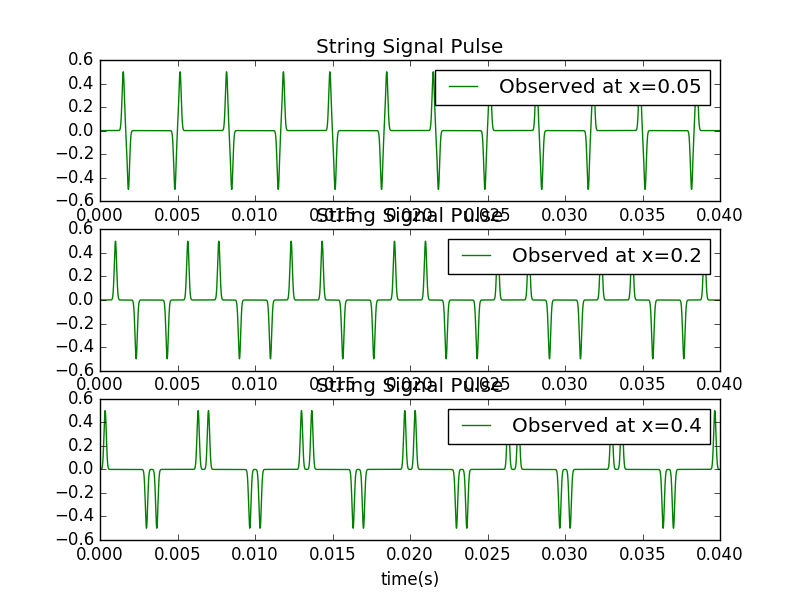
Now we observe the behavior of the signal with different places.

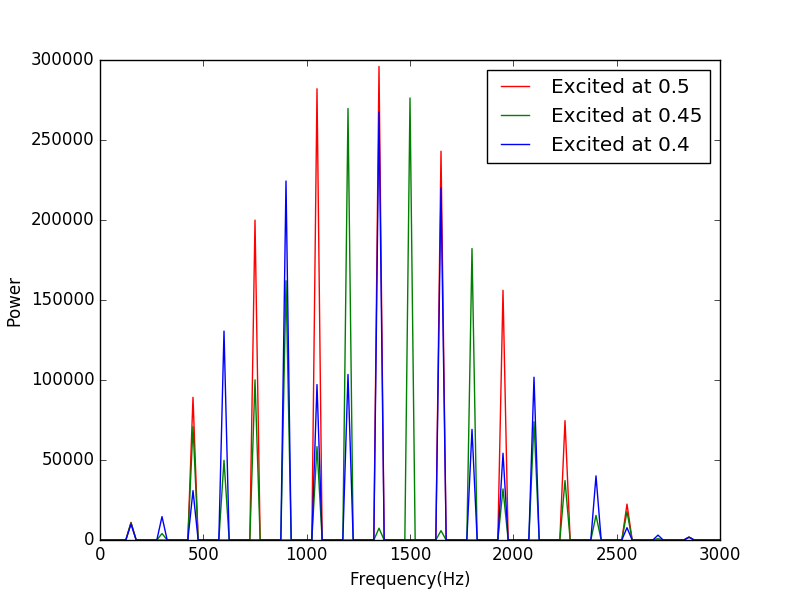
Here are the spectrum of the above signal.Here the string was excited at the center.

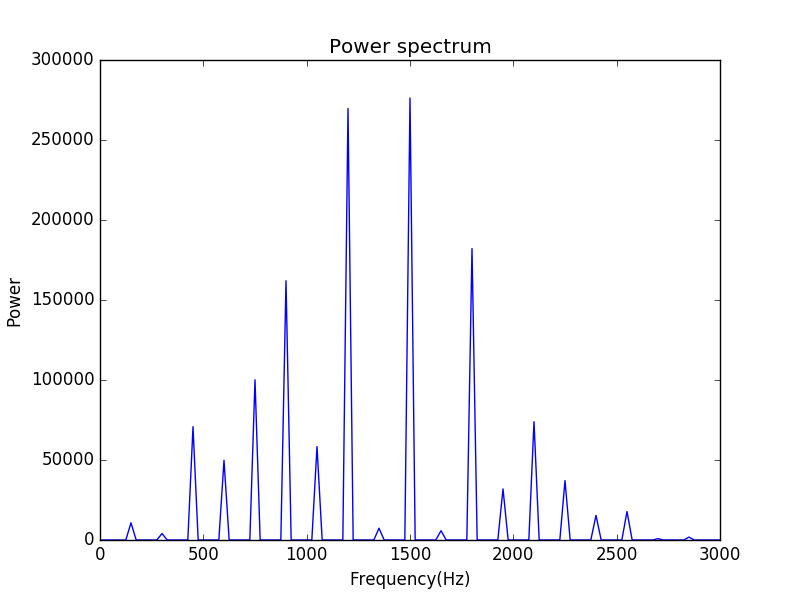
Now we combine both of these picture in order to gave a relatively clear configuration.

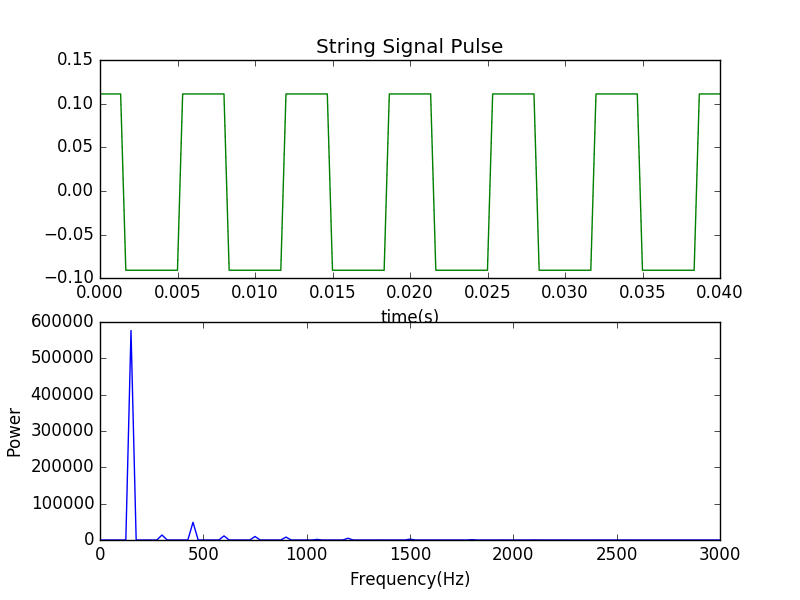
Now the intial wave packet was a real one.

The two colors specify two slightly seperated excited points.Here you can observe some disapperance of the frequency.The reason is that the only Fourier components with significant amplitudes will be those that are nonzero at the center of the string and are symmetric about the center.Hence the Fourier components,which have zero ampltitude.

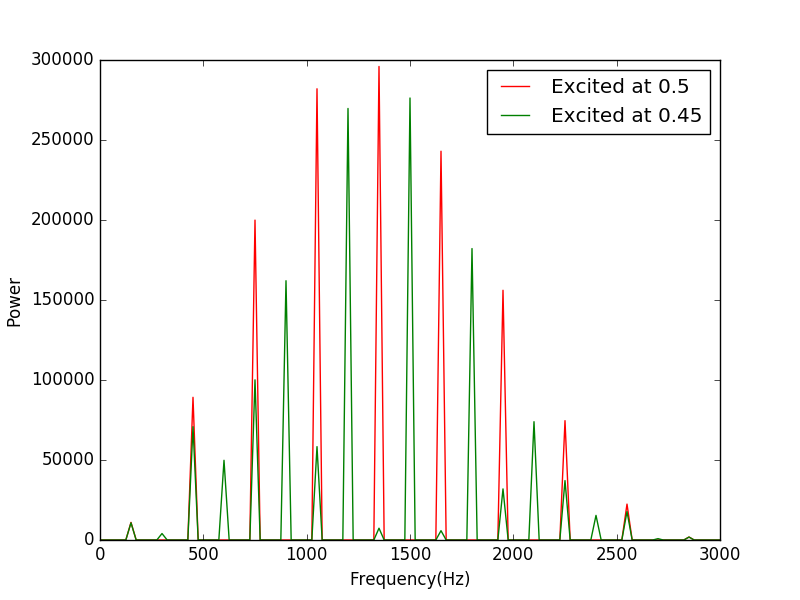
Now we can see the appearance of some already-disappeared frequency.The message of this exercise is that the frequencies that are excited will be those whose spatial modes have the same symmetry as that of the intial wavepacket.

6 Vpython

Here I found a program written by others in Vpython.org

7 Acknowledge

1.Junyi Shangguan
2.Feng Chen
3.Wikipedia.