The Homework of Chapter Four and Five

Author： 宗玥 2014301020004

Statistical-and-Thermal-Physics

---

Problem 4.1. Simple example

(a) What is the mean value of spin 2 in the above example? Why is its mean value not zero?

(a)

$$\begin{eqnarray*} \overline{s}_2&=&\sum_{i=1}^{10}P_is_{2,i}\\ &=&\frac{1}{10}[6*(+1)+4*(-1)]=\frac15 \end{eqnarray*}$$

(b) What is the probability p that a given spin points up?

(b) $\frac35$

(c) What is the probability that if spin 1 is up, then spin 2 also is up?

(c) $\frac12$

Problem 4.2. Counting microstates

(a) Consider N = 4 noninteracting spins with magnetic moment µ that can point either parallel or antiparallel to the magnetic field B. If the total energy E =−2µB, what are the accessible microstates and the probability that a particular spin is up or down?

(a) The total energy E=-2μB, then 3 spins are up. The number of accessible microstates is 4. The probability that a paricular spin is up is $\frac13$

(b) Consider N = 9 noninteracting spins with total energy E = −µB. What is the number of up spins, the number of accessible microstates, and the probability that a particular spin is up or down?

(b) The number of up spins is 5, the number of accessible microstates is 126, the probability that a particular spin is up is $\frac59$

Problem 4.3. Probability of particles moving in the same direction

Consider a one-dimensional ideal gas consisting of N = 5 particles each of which has the same speed v, but can move in one of two directions with equal probability. The velocity of each particle is independent. What is the probability that all the particles are moving in the same direction?

$2/2^5=1/16$

Problem 4.4. An Einstein solid

(a) Verify that (4.3) yields the correct answers for N = 3 and E = 3.

(a)

$$\Omega=\frac{(3+3-1)!}{3!(3-1)!}=10$$
The answer is equal to what we get above, so (4.3) is correct.

(b) What is the number of microstates for an Einstein solid with N = 4 and E = 6?

(b)

$$\Omega=\frac{(6+4-1)!}{6!(4-1)!}=84$$

(c) Suppose that N = 3 and E = 3 and the particles are labeled red, white, and blue. What is the probability that the red particle has energy equal to one?

(c) $3/10$

(d) Given that the red particle has energy 1, what is the probability that the blue particle

(d) $1/3$

Problem 4.5. Standard deviation of the energy of subsystem A

Use the results of Table 4.4 to find the standard deviation of the energy of subsystem A.

$$\begin{eqnarray*} \overline E_A&=&E(\overline E_A)=3\\ E(\overline E^2_A)&=&12\\ Var(E_A)&=&E(\overline E^2_A)-(E(E_A))^2=3\\ \sigma_{E_A}&=&\sqrt{Var(E_A)}=\sqrt{3} \end{eqnarray*}$$

Problem 4.6. Two Einstein solids in thermal contact

(a) The internal constraint is removed so that the two subsystems may exchange energy. Determine the probability PA(EA) that system A has energy EA. Plot PA versus EA and discuss its qualitative energy dependence.

(a)

$E_A$	$P$
0	0
1	0.03
2	0.06
3	0.09
4	0.11
5	0.13
6	0.14
7	0.13
8	0.11
9	0.09
10	0.06
11	0.03
12	0

(b) What is the probability that energy is transferred from system A to system B and from system B to system A? What is the probability that energy goes from the hotter to the colder system? How does this probability compare to the probability found from Table 4.3 for a smaller system? Which system was hotter initially?

(b) The probability that energy is transferred from system A to system B is 0.97. The probability that energy is transferred from system B to system A is 0.03. It just seem like the energy goes from the hotter to the colder system, and the system A is hotter initially.

(c) What is the number of accessible microstates for the composite system after the internal constraint has been relaxed? What is the change in the total entropy of the system (choose units such that k = 1)?

(c) The number of accessible microstates for the composite system after the internal constraint has been relaxed is 455. The total entropy of the system is 6.12

(d) Determine the mean energy EA, the most probable energy ˜ EA, the standard deviations σA and σB, and the relative fluctuations σA/EA. How does the value of this ratio compare with the value of the ratio calculated in Table 4.3?

(d)

$$\begin{eqnarray*} \overline E_A&=&6\\ \tilde E_A&=&6\\ \sigma_A&=&6.26\\ \sigma_B&=&6.26\\ \frac{\sigma_A}{\overline E_A}&=&1.043\\ \end{eqnarray*}$$
In table 4.3 the ratio is $\sqrt 3/3\approx 0.577$, which is smaller than it

(e) The entropy of the composite system when each subsystem is in its most probable macrostate is lnΩA( ˜ EA)ΩB(Etot − ˜ EA). Compare the value of this contribution to the value of the total entropy, lnPEA ΩA(EA)ΩB(Etot −EA), calculated in part (c)? (f) *Consider successively larger systems and describe the qualitative behavior of the various quantities.

(e)

$$ln\Omega_A(\tilde E_A )\Omega_B(E_{tot}-\tilde E_A)=ln 49=3.89$$
In (c) the total entropy is $6.12$

Problem 4.7. More on two Einstein solids in thermal contact

(a) Explore the effect of increasing the values of NA, NB, and the total energy Etot. Discuss the qualitative dependence of SA, SB, and Stot on the energy EA. In particular, explain why SAis an increasing function of EA and SB is a decreasing function of EA. Given this dependence of SA and SB on EA, why does Stot have a maximum at a particular value of EA?

(a) The function of entropy equals $kln\Omega$. While $E_A$ is encreasing the number of microstate of system A is also increasing and for system B is decreasing. When $\Omega_A=\Omega_B$, the number of microstate of the total system is the biggest, which means the $S_{tot}$ have a maximum value in this situation.

(b) The values of the magnitudes of the inverse slopes dSA/dEA and dSB/dEB can be obtained by clicking on the corresponding curves. The values of the magnitudes of the inverse slopes are given in the lower right corner. What is the relation of these slopes to the temperature? Determine the value of EA at which the slopes are equal. What can you say about the total entropy at this value of EA? Consider a number of different values for NA, NB and Etot. Be sure to include a case where NA 6= NB.

(b) When temperature is increasing the inverse slopes are increasing. When $E_A=100$ the slopes are equal. When $N_A=N_B$ the total entropy at this value of $E_A$ is at its maxmum . However when $E_A \ne E_B$, the total entropy at this point is not the maximum.

Problem 4.8. More on Einstein solids

(a) Choose E = 200 and NA = NB = 4 and estimate the width of PA(EA). [Estimate the width at half the maximum value of PA(EA).] Repeat for NA = NB = 16 and NA = NB = 64. How does the width depend on the number of particles? For example, does the width decrease linearly or by some other power of the number of particles?

(a) When $E$= 200, $N_A=N_B=4$ the width of $P_A(E_A)=6$. When $N_A=N_B=16$, the width is almost 3. When $N_A=N_B=64$, the width is almost 2. The larger number of partical the smaller width exist.

(b) Repeat part (a) but with E = 20. Do you obtain the same dependence of the width on the number of particles. If not, why not?

(b) Yes

(c) Consider E = 200, NA = 1, and NB = 15. What is the nature of PA(EA)? Explain why the curve is a decreasing function of EA.

(c) $P_A(E_A)$ shows the probability of the energy that A can get. At this situation the number of particle A is 1, which is less than B. When $E_A$ is large, the energy can transfer from A to B easily, so that the curve is high. When $E_A$ is not large enough. It is hard for A get energy from B. So the curve is low. Thus the curve is adecreasing function of $E_A$.

Problem 4.9. Qualitative behavior of the probabilities

(a) In Table 4.3 we considered a composite Einstein solid of four particles with two particles in each subsystem. Use the results of Table 4.3 to calculate the probability that subsystem A is in a particular microstate.

(a) The probability of each microstate is $1/84$

(b) The program computes the probability PA(EA) that subsystem A has energy EA. Consider NA = 4, NB = 12 and Etot = 3. Run the program and collect the data from the Data Table under the Views menu.

(b)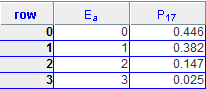

(c) Determine the probability Ps(Es) that subsystem A is in a particular microstate by dividing PA(EA) by the number of microstates with energy EA. Plot Ps(Es).

(c)

$E_A$	$P_S(E_A)$
0	0.1487
1	0.0955
2	0.0147
3	0.00125

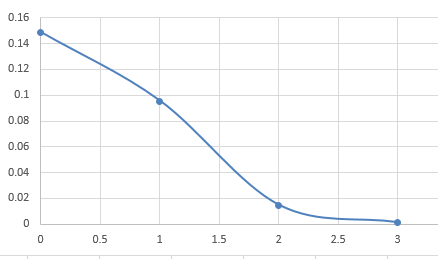
(d) Explain why the probabilities Ps and PA(EA) are not the same. Why is the probability Ps(Es) a monotonically decreasing function of Es? What is the qualitative behavior of PA(EA)?

(d) Because the number of microstate with energy $E_A$ is not same. The larger $E_A$ has larger number of microstate, so $P_S(E_S)$ is decreasing function of $E_S$. And the larger $E_A$, the less $P_A(E_A)$

Problem 4.10. Rapid increase in the number of states

(a) Consider an Einstein solid of N = 20 distinguishable particles. What is the total number of accessible microstates Ω(E) for E = 10, 102, 103,...? Is Ω(E) a rapidly increasing function of E for fixed N?

(a) When E=10, $\Omega_E=92.378$. When E=100, $\Omega_E=11271.003$. When E=1000, $\Omega_E=94600$
So it is clear that $\Omega_E$ is a rapidly increasing function of E for fixed N

(b) Is Ω a rapidly increasing function of N for fixed E?

(b) Yes it is

Problem 4.11.

Suppose that the energy of an electron in a one-dimensional box of length L is E = 144(h2/8mL2). How many microstates are there with energy less than or equal to this value of E?

$$E=144\frac{\hbar^2}{8mL^2}=\frac{n^2\hbar^2}{8mL^2}$$
So n=12, which is The number of microstates with energy less than or equal to this value of E.

Problem 4.12. Finite-size effects in two dimensions

The expression (4.39) for Γ(E) is valid only for large E because the area of a quadrant of a circle overestimates the number of lattice points nx,ny inside a circle of radius R. Use Program IdealGasNumberOfStates to explore how the relation Γ = πR2/4 approximates the actual number of microstates. The program computes the number of nonzero, positive integers that satisfy the condition n2 x + n2 y ≤ R2. What is the minimum value of R for which the difference between the asymptotic relation and the exact number is less than 1%?

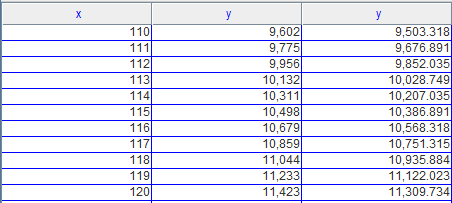
We can get when R=117, the asymptotic relation and the exact number is 0.00992. When R=116, that is 0.01036. So the minimum value of R is 117.

Problem 4.15. Approximate expression for Γ(E,V,N)

We can obtain an approximate expression for Γ(E,V,N) using simpler physical considerations. We write

$$Γ(E,V,N) ≈ \frac{1}{ N!} Γ_1(\frac{E}{ N} ,V)Γ_1(\frac{E}{ N} ,V)···Γ_1(\frac{E}{ N} ,V)= \frac{1}{ N!} Γ_1(\frac{E}{ N} ,V)^N, (4.52)$$
where Γ 1(E,V ) is the number of states of a single particle with energy less than E in a threedimensional box of volume V . We have assumed that on the average each particle has an energy E/N. Find the form of Γ(E,V,N) using the relation (4.42) for Γ1. How does the dependence on V and E of Γ(E,V,N) obtained from this simple argument compare to the V and E dependence of Γ in (4.49). What about the N dependence?

$$\begin{eqnarray*} \Gamma_1(\frac{E}{N},V)&=&\frac{4\pi}{3}\frac{V}{h^3}(2m\frac{E}{N})^{3/2}\\ \Gamma(E,V,N)&=&\frac{1}{N!}\Gamma_1(\frac{E}{N},V)^N\\ &=&\frac{1}{N!}(\frac{4\pi}{3}\frac{V}{h^3}(2m\frac{E}{N})^{3/2})^N\\ &=&\frac{1}{N!}(\frac{V}{h^3})^N(\frac{4\pi}{3})^N \frac{(2mE)^{3N/2}}{N^{3N/2}} \end{eqnarray*}$$
In (4.49)
$$\Gamma(E,V,N)=\frac{1}{N!}(\frac{V}{h^3})^{N}\frac{(2\pi mE)^{3N/2}}{(3N/2)!}$$
The dependence on V and E for two function is equal. The N dependence (4.49) is higher.

Problem 4.16. Density of states of an ideal gas

Use (4.51) to calculate the density of states g(E,V,N) and verify that Γ(E,V,N) and g(E,V,N) are rapidly increasing functions of E,V , and N.

$$\begin{eqnarray*} ln\Gamma(E)&=&Nln\frac VN+\frac32Nln\frac{mE}{3N\hbar^2}+\frac52N\\ \Gamma&=&exp(Nln\frac VN+\frac32Nln\frac{mE}{3N\hbar^2}+\frac52N)\\ g(E)&=&\frac{d\Gamma}{dE}\\ &=&\frac{3N}{2E}exp(Nln\frac VN+\frac32Nln\frac{mE}{3N\hbar^2}+\frac52N)\\ \end{eqnarray*}$$

Problem 4.17. Form of the entropy

Compare the form of S given in (4.63) with the form of S determined from thermodynamic considerations in Section 2.19.

In (4.63)

$$S(E,V,N)=Nk[ln\frac{V}{N}+\frac32ln\frac{mE}{3N\pi \hbar^2}+\frac52]$$
In section 2.19
$$\Delta S=\frac32 Nkln\frac{T_2}{T_1}+Nkln\frac{V_2}{V_1}$$
$$\begin{eqnarray*} \Delta E&=&S(E_2,V_2,N)-S(E_1,V_1,N)\\ &=&Nkln\frac{V_2}{N}\frac{N}{V_1}+\frac32Nkln\frac{mE_2}{3N\pi \hbar^2}\frac{3N\pi \hbar^2}{mE_1}\\ &=&Nkln\frac{V_2}{V_1}+\frac32Nkln\frac{E_2}{E_1}\\ &=&\frac32 Nkln\frac{T_2}{T_1}+Nkln\frac{V_2}{V_1} \end{eqnarray*}$$

Problem 4.18. Equivalent definitions of the entropy

Verify the result (4.63) for the entropy S of an ideal gas using either of the definitions of S given in (4.62). Why can we neglect ∆E compared to E when we use the definition (4.62a)?

For (4.62b)

$$\begin{eqnarray*} ln\Gamma(E,V,N)&=&Nln\frac{V}{N}+\frac32Nln\frac{nE}{3N\pi \hbar^2}+\frac52 N\\ S(E,V,N)&=&kln\Gamma(E,V,N)\\ &=&kN[ln\frac{V}{N}+\frac32ln\frac{nE}{3N\pi \hbar^2}+\frac52 ]\\ \end{eqnarray*}$$

Problem 4.19. The Sackur-Tetrode expression for the entropy

Use the relations (4.63) and (4.65) to obtain S as a function of T, V , and N instead of E, V , and N. This relation is known as the Sackur-Tetrode equation.

$$\begin{eqnarray*} S(E,V,N)&=&Nk[ln\frac{V}{N}+\frac32ln\frac{mE}{3N\pi \hbar^2}+\frac52]\\ E&=&\frac32NkT\\ S&=&Nk[ln\frac{V}{N}+\frac32ln\frac{\frac32 mNkT}{3N\pi \hbar^2}+\frac52]\\ &=&Nk[ln\frac{V}{N}+\frac32ln\frac{mkT}{2\pi \hbar^2}+\frac52] \end{eqnarray*}$$

Problem 4.20. The chemical potential of an ideal gas

Use (4.61) and (4.63) to derive the dependence of the chemical potential µ on E, V , and N for an ideal classical gas. Then use (4.65) to determine µ(T,V,N). We will derive µ(T,V,N) for the ideal classical gas more simply in Section 6.6.

$$\begin{eqnarray*} S(E,V,N)&=&Nk[ln\frac{V}{N}+\frac32ln\frac{mE}{3N\pi \hbar^2}+\frac52]\\ \frac{\mu}{T}&=&-(\frac{\partial S}{\partial N})_{E,V}\\ &=&-k(ln\frac{V}{N}+\frac32ln\frac{mE}{3N\pi \hbar^2}+\frac52)+\frac52k\\ &=&-k(ln\frac{V}{N}+\frac32ln\frac{mE}{3N\pi \hbar^2})\\ \mu&=&-\frac{2E}{3N}(ln\frac{V}{N}+\frac32ln\frac{mE}{3N\pi \hbar^2})\\ &=&kT(ln\frac{V}{N}+\frac32ln\frac{mkT}{2\pi \hbar^2}) \end{eqnarray*}$$

Problem 4.21. The energy as a function of the temperature

Solve (4.72) for n/N and verify (4.74). Then use (4.14) to solve for E as a function of T and verify (4.73) for a system of N noninteracting spins.

$$\begin{eqnarray*} \frac{1}{T}&=&-k\frac{1}{2\mu B}ln\frac{N-n}{n}\\ -\frac{2\mu B}{kT}&=&ln\frac{N-n}{n}\\ ne^{-2\mu B/kT}&=&N-n\\ N&=&n(1+e^{-2\mu B/kT})\\ p&=&\frac{n}{N}=\frac{1}{1+e^{-2\mu B/kT}}　　（4.74）\\ E&=&-(2n-N)\mu B\\ &=&-(1-e^{-2\mu B/kT})n\mu B\\ &=&-(1-e^{2\beta \mu B})\frac{e^{\beta \mu B}}{e^{\beta \mu B}+e^{-\beta \mu B}}N\mu B\\ &=&-\frac{e^{\beta \mu B}-e^{-\beta \mu B}}{e^{\beta \mu B}+e^{-\beta \mu B}}N\mu B\\ &=&-N\mu Btanh(\beta \mu B)　　　(4.73)\\ \end{eqnarray*}$$

Problem 4.22. The Einstein solid in the microcanonical ensemble

Consider a collection of N distinguishable harmonic oscillators with total energy E. The oscillators are distinguishable because they are localized on different lattice sites. In one dimension the energy of each particle is given by ǫn = (n + 1 2)~ω, where ω is the angular frequency. Hence, the total energy can be written as E = (Q + 1 2N)~ω, where Q is the number of quanta. Calculate the dependence of the temperature T on the total energy E in the microcanonical ensemble using the result that the number of accessible microstates in which N distinguishable oscillators can share Q indistinguishable quanta is given by Ω = (Q + N −1)!/Q!(N −1)! [see (4.3)]. Then use this relation to find E(T). This relation is calculated much more simply in the canonical ensemble as shown in Example 4.3.

$$\begin{eqnarray*} \frac1T&=&(\frac{\partial S}{\partial E})_{E,N}\\ &=&\frac{\partial S}{\partial Q}\frac{\partial Q}{\partial E}\\ E&=&(Q+\frac12N)\hbar \omega\\ Q&=&\frac{E}{\hbar \omega}-\frac12N\\ S&=&kln\Omega\\ &=&kln\frac{(Q+N-1)!}{Q!(N-1)!}\\ &=&k[(Q+N-1)ln(Q+N-1)-QlnQ-(N-1)ln(N-1)]\\ \frac1T&=&\frac{k}{\hbar\omega}[ln(\frac{E}{\hbar\omega}+\frac12N-1)+1-ln(\frac{E}{\hbar\omega}-\frac12N)-1]\\ &=&\frac{k}{\hbar\omega}[ln(\frac{E}{\hbar\omega}+\frac12N-1)-ln(\frac{E}{\hbar\omega}-\frac12N)]\\ E&=&N\hbar\omega[\frac12+\frac{1}{e^{\beta \hbar\omega}-1}] \end{eqnarray*}$$

Problem 4.23.

Discuss the relation between the qualitative results that we obtained based on Table 4.6 and the Boltzmann distribution in (4.79).

From Table 4.6 we know that $P_n\varpropto e^{-\beta \varepsilon_n}$
In (4.79) $P_s=\frac1Ze^{-\beta E_s}$
So they are same.

Problem 4.24. Relative abundance of two isomers

The hydrocarbon 2-butene, CH3-CH=CH-CH3, occurs in two isomers (geometrical structures) called cis and trans. The cis (on this side) isomer of 2-butene has both CH3 groups on the same side of the C=C double bond. In the trans (across) isomer the CH3 groups are on opposite sides of the double bond (see Figure 4.7). The energy difference ∆E between the two conformations is approximately ∆E/k = 4180K, with the trans isomer lower than the cis isomer. Determine the relative abundance of the two conformations at T = 300K and T = 1000K.

At 300K, $P_{cis}/P_{trans}=e^{\Delta E/kT}=1.1*10^6$
At 1000K, $P_{cis}/P_{trans}=e^{\Delta E/kT}=65$
So the probability to get trans isomer has been increased sharply

Problem 4.25. Distribution of energy in the canonical ensemble

Given what you have learned so far about the N dependence of the relative energy fluctuations, what is your best guess for the form of the probability that a system in equilibrium with a heat bath at temperature T has energy between E and E +∆E? The form of the probability distribution of the energy of a system in the canonical ensemble is derived in Section 4.14.2.

Even though the system is in equilibrium, the energy also have fluctuations. The range of this fluctuation is E and E+ΔE

Problem 4.26.

The Boltzmann probability given by (4.79) is the probability that the system is in a particular microstate with energy Es. On the basis of what you have learned so far, what do you think is the form of the probability p(E)∆E that the system has energy between E and E + ∆E?

$$\begin{eqnarray*} g(E)\Delta E&=&P(E+\Delta E)-P(E)\\ &=&\frac{dP(E)}{dE}\Delta E\\ &=&\frac{d}{dE}(\frac{e^{-\beta E_s}}{\Sigma_s e^{-\beta E_s}})\Delta E\\\ &=&\frac{-\beta e^{-\beta E}\Delta E}{\Sigma_s e^{-\beta E_s}} \end{eqnarray*}$$

Problem 4.27. Entropy of the ground state of a system of electrons

Explain why the entropy associated with the ground state of a system of N electrons is kN ln2 in zero magnetic field.

For the ground state of a system of N electrons, the number of its microstates $\Omega=2^N$. According to (4.100), we get

$$S=kln\Omega=kln2^N=kNln2$$

Problem 4.28. Thermodynamic properties of a system of harmonic oscillators

(a) Show that for one oscillator

$$\begin{eqnarray*} f &=&\frac1 2\hbar ω + kT ln(1−e^{−β\hbar ω}), (4.130) \\ s &=& k[\frac{ β\hbar ω}{ e^{β\hbar ω} −1} −ln(1−e^{−β\hbar ω})], (4.131) \\ \bar e &=&\hbar ω[\frac 1 2 +\frac{ 1}{ e^{β\hbar ω} −1}]. (4.132) \end{eqnarray*}$$
Equation (4.132) is Planck’s formula for the mean energy of an oscillator at temperature T. The heat capacity is discussed in Problem 4.50.

(a)
For one dimensional harmonic oscillator,

$$Z_1=\frac{e^{-\beta \hbar \omega/2}}{1-e^{-\beta \hbar \omega}}$$
$$lnZ_1=-\frac12\beta \hbar \omega -ln(1-e^{-\beta \hbar \omega})$$
Thus, we can show that
$$\begin{eqnarray*} f&=&-kTlnZ_1\\ &=&-kT(-\frac12\beta \hbar \omega -ln(1-e^{-\beta \hbar \omega}))\\ &=&\frac12\hbar \omega+kTln(1-e^{-\beta \hbar \omega})　　（4.130）\\ s&=&-(\frac{\partial f}{\partial T})_V\\ &=&-\frac{\partial}{\partial T}(kTln(1-e^{-\beta \hbar \omega}))\\ &=&-(kln(1-e^{-\beta \hbar \omega})+kT\frac{\frac{1}{kT^2}\hbar \omega}{e^{\beta \hbar \omega}-1})\\ &=&k[\frac{\beta\hbar\omega}{e^{\beta \hbar\omega}-1}-ln(1-e^{-\beta\hbar\omega})]　　（4.131）\\ \bar e&=&-\frac{\partial}{\partial \beta}lnZ_1\\ &=&\frac{\partial}{\partial \beta}[\frac12\beta \hbar \omega -ln(1-e^{-\beta \hbar \omega})]\\ &=&\frac12\hbar\omega-\frac{-e^{-\beta\hbar\omega}\hbar\omega}{1-e^{-\beta\hbar\omega}}\\ &=&\hbar\omega[\frac12+\frac{1}{e^{\beta\hbar\omega}-1}]　　（4.132） \end{eqnarray*}$$

(b) Given the result (4.132), what is the mean energy of a system of N harmonic oscillators in equilibrium with a heat bath at temperature T?

(b)

$$\begin{eqnarray*} Z_N&=&Z_1^N\\ \overline E&=&-\frac{\partial}{\partial \beta}lnZ_N\\ &=&-N\frac{\partial}{\partial \beta}lnZ_1\\ &=&N\hbar\omega[\frac12+\frac{1}{e^{\beta\hbar\omega}-1}] \end{eqnarray*}$$

(c) Compare your answer with the result for the energy of N harmonic oscillators calculated in the microcanonical ensemble in Problem 4.22. Do the two ensembles give identical results?

(c) They are the same result

Problem 4.34. Simulation of hard disks

(a) Run the simulation with the default parameters and record the density and the results for PA/NkT and the temperature. Is the temperature a useful quantity for hard disks? Does it fluctuate during the simulation. If not why not? Does the pressure P fluctuate?

(a)

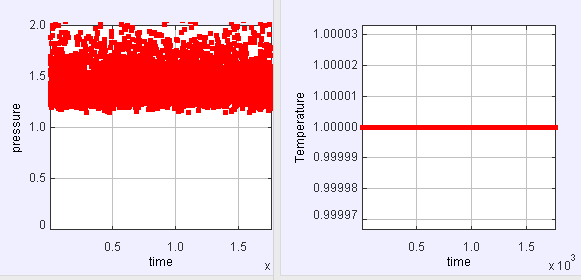
Apparently during the whole simulation the value of T is unchanged. Even though it is a useful quantity for hard disks, it doesn't fluctuate. However the pressure P fluctuates.

(b) *Compute PA/NkT as a function of density for a fixed number of particles. Is there any evidence of a phase transition where the slope of the pressure with respect to density changes abruptly?

(b)

Problem 5.1. Comparison of the results for two ensembles

(a) Compare the result (5.6) for the mean energy E(T) of a system of noninteracting spins in the canonical ensemble to the result that you found in Problem 4.21 for T(E) using the microcanonical ensemble.

(a) The result (5.6) for the mean energy $\bar E(T)$ is equal to the result we found in Problem 4.21

$$\overline E(T)=-N\mu Btanh(\beta \mu B)$$
$$E=-N\mu Btanh(\beta \mu B)$$
They are same

(b) Why is it much easier to treat a system of noninteracting spins in the canonical ensemble?

(b) Because in the canonical ensemble system, T,V,N is fixed. When we try to find the result for the mean energy as a function of T, we will find it much easier.

(c) What is the probability p that a spin is parallel to the magnetic field B given that the system is in equilibrium with a heat bath at temperature T? Compare your result to the result in (4.74) using the microcanonical ensemble.

(c)

$$p=\frac{e^{\frac{\mu B}{kT}}}{e^{\frac{\mu B}{kT}}+e^{-\frac{\mu B}{kT}}}$$

(d) What is the relation of the results that we have found for a system of noninteracting spins to the results obtained in Example 4.2?

(d) For the result we have found for a system of noninteracting spins, when we set N=2, we will get the result in Example 4.2.

Problem 5.2.

Relation of the susceptibility to the magnetization fluctuations Use considerations similar to that used to derive (5.15b) to show that the isothermal susceptibility can be written as

$$χ =\frac{1}{ kT}[\overline {M^2} −\overline M^2] . (5.17)$$ Note the similarity of the form (5.17) with the form (4.88) for the heat capacity $C_V$

$$\begin{eqnarray*} \overline {M^2}&=&\frac{1}{Z}\sum_s M^2 e^{-\beta(E_{0,s}-M_sB)}\\ &=&\frac{1}{\beta^2 Z}\frac{\partial^2Z}{\partial B^2}\\ \overline M&=&\frac{1}{\beta Z}\frac{\partial Z}{\partial B}\\ \chi&=&(\frac{\partial M}{\partial B})_T\\ &=&\frac{\partial}{\partial B}(\frac{1}{\beta Z}\frac{\partial Z}{\partial B})\\ &=&-\frac{1}{\beta Z^2}(\frac{\partial Z}{\partial Z})^2+\frac{1}{\beta Z}\frac{\partial^2Z}{\partial B^2}\\ &=&\beta[\frac{1}{\beta^2Z}\frac{\partial^2Z}{\partial B^2}-\frac{1}{\beta^2Z^2}(\frac{\partial Z}{\partial Z}^2)]\\ &=&\frac{1}{kT}[\overline{M^2}-\overline M^2] \end{eqnarray*}$$ .

Problem 5.3. Thermodynamics of noninteracting spins

(a) Plot the magnetization given by (5.18) and the heat capacity C given in (5.8) as a function of T for a given external magnetic field B. Give a simple argument why C must have a broad maximum somewhere between T = 0 and T =∞.

(a)

$$\begin{eqnarray*} M&=&N\mu tanh(\beta \mu B)\\ &=&N\mu tanh(\frac{\mu B}{kT})\\ C&=&kN(\beta \mu B)^2sech^2\beta\mu B\\ &=&kN(\frac{\mu B}{kT})^2sech^2\frac{\mu B}{kT} \end{eqnarray*}$$
This function must increses first and then decreses, which means it must have a broad maximum somewhere between T=0 and T=∞

(b) Plot the isothermal susceptibility χ versus T for fixed B and describe its limiting behavior for low temperatures.

(b)

$$\chi=\frac{N\mu^2}{kT}sech^2(\frac{\mu B}{kT})$$
When T is low enough, $\chi \to 0$

(c) Calculate the entropy of a system of N noninteracting spins and discuss its limiting behavior at low (kT ≪ µB) and high temperatures (kT ≫ µB). Does S depend on kT and µB separately?

(c)

$$\begin{eqnarray*} S&=&-(\frac{\partial F}{\partial T})_{V,N}\\ &=&-\frac{\partial}{\partial T}(-NkTln(2cosh\frac{\mu B}{kT}))\\ &=&Nkln(2cosh\frac{\mu B}{kT})+NkT(-\frac{\mu B}{kT^2}tanh\frac{\mu B}{kT})\\ &=&NK[ln(2cosh\frac{\mu B}{kT})-\frac{\mu B}{kT}tanh\frac{\mu B}{kT}] \end{eqnarray*}$$
When $kT\ll\mu B$, $S\to 0$
When $kT\gg\mu B$, $S\to Nkln2$

Problem 5.4. Adiabatic demagnetization

(a) If B = 4 tesla, at what temperature is 75% of the spins oriented in the +z direction?

(a)

$$\begin{eqnarray*} p&=&\frac{e^{\frac{\mu B}{kT}}}{e^{\frac{\mu B}{kT}}+e^{\frac{-\mu B}{kT}}}=0.75\\ e^{\frac{\mu B}{kT}}&=&3e^{-\frac{\mu B}{kT}}\\ T&=&\frac{2\mu B}{kln3}=4.89K \end{eqnarray*}$$

(b) Assume that N = 1023, T = 1K, and B is increased quasistatically from 1tesla to 10tesla. What is the magnitude of the energy transfer from the heat bath?

(b)

$$\begin{eqnarray*} \Delta E&=&-N\mu 10 tanh\frac{10\mu}{kT}+N\mu tanh\frac{\mu}{kT}\\ &=&-0.38J \end{eqnarray*}$$

(c) If the system is now thermally isolated at T = 1K and B is quasistatically decreased from 10tesla to 1tesla, what is the final temperature of the system? This process is known as adiabatic demagnetization. (This problem can be solved without elaborate calculations.)

(c)

$$\begin{eqnarray*} E_1&=&-N\mu10tanh\frac{10\mu}{kT_1}\\ E_2&=&-N\mu tanh\frac{\mu}{kT_2}\\ E_1&=&E_2\\ T_2&=&1.185K \end{eqnarray*}$$