张梓桐计算物理第十一次作业

1 Problem

4.19 4.20

2 Abstract

Three-body system is famous for its complexity and an analytical solution is known not to exist. This is where numerical solutions can show its values in scientific significance.
It is known that te motion of asteriods located near the Kirkwood gaps is believed to be chaotic.And there is various chaotic motion of planet which will be a fairly difficult stimulation.However,there is one case of chaos in our solar system that is accessible to a fairly simple stimulation,that is the Hyperion.In this passage,we are going to investigate the properities of the movement of Hyperion.And the behavior of two slightly different intial conditions.

3 Background.

3.1 Physical characteristics

Hyperion, also known as Saturn VII, is a moon of Saturn discovered by William Cranch Bond, George Phillips Bond and William Lassell in 1848. It is distinguished by its irregular shape, its chaotic rotation, and its unexplained sponge-like appearance. It was the first non-round moon to be discovered.

One interseting phenomenon that the moons of the Earth spins about its axis in such a way that it always keeps one particular side facing Earth.That is,its spin is synchronized with its orbital motion about Earth.

The Voyager 2 images and subsequent ground-based photometry indicated that Hyperion's rotation is chaotic, that is, its axis of rotation wobbles so much that its orientation in space is unpredictable. Its Lyapunov time is around 30 days. Hyperion, together with Pluto's moons Nix and Hydra,is among only a few moons in the Solar System known to rotate chaotically, although it is expected to be common in binary asteroids. It is also the only regular planetary natural satellite in the Solar System known not to be tidally locked.---Wikipedia

The formulation of the synchronized spin is not discussed here,it's clearly illustrated in the text book on page 123.Additionally,it turns out that all of the moons in the solar system except one exhibit such synchronism.The exception is Hyperion.

Hyperion is unique among the large moons in that it is very irregularly shaped, has a fairly eccentric orbit, and is near a much larger moon, Titan. These factors combine to restrict the set of conditions under which a stable rotation is possible. The 3:4 orbital resonance between Titan and Hyperion may also make a chaotic rotation more likely. The fact that its rotation is not locked probably accounts for the relative uniformity of Hyperion's surface, in contrast to many of Saturn's other moons, which have contrasting trailing and leading hemispheres.---Wikipedia

First published in 1989, Hyperion has the structure of a frame story, similar to Geoffrey Chaucer's Canterbury Tales and Giovanni Boccaccio's Decameron. The story weaves the interlocking tales of a diverse group of travelers sent on a pilgrimage to the Time Tombs on Hyperion. The travelers have been sent by the Church of the Final Atonement, alternately known as the Shrike Church, and the Hegemony (the government of the human star systems) to make a request of the Shrike. As they progress in their journey, each of the pilgrims tells their tale.
。

Hyperion 亥伯龙是希腊神话中的一位巨人的名字，该亚与乌拉诺斯儿子,Helios赫利俄斯(太阳神）的父亲。
也是月亮神和缪斯女神之父，中文又译作“许珀里翁”、“亥帕瑞恩”等。

3.2 Calculation Part

To simulate the motion of Hyperion we will first make few simplifying assumptions.Our goal will not be to perform a relastic simulations.Rather,our objective is simply to show that the motion of such an irregularly shaped moon can be chaotic.With that goal in mind we consider the model with two bodies.We have two particles $m_1$ and $m_2$,connected by a massless rod in orbit around a massive object located at the origin.
There are two forces acting on each of the masses,the force of gravity from Saturn and the force from the rod.Since we are interested in the motion about the center of mass,the force from the rod does not contribute.

$$\begin{eqnarray*} \vec F_1=-\frac{GM_sat m_1}{r_1^3}(x_1\vec i +y_1 \vec j) \end{eqnarray*}$$ .
The coordinateed of the center of mass are $(x_c,y_c)$,so that $(x_1-x_c)\vec i +(y_1-y_c)\vec j$ is the vector from the center of mass to $m_1$.The torque on $m_1$ is then:
$$\begin{eqnarray*} \vec \tau_1=[(x_1-x_c)\vec i +(y_1-y_c)\vec j]\times \vec F_1 \end{eqnarray*}$$
With a similiar expression for $\vec \tau_2$.The total torque on the moon is just $\vec \tau_1+\vec \tau_2$,and this is related to the time derivtive of $\omega$ by:
$$\begin{eqnarray*} \frac{d\vec w}{dt}=\frac{\vec \tau_1+\vec \tau_2}{I} \end{eqnarray*}$$
where $I=m_1|r_1|^2+m_2|r_2|^2$ is the moment of inertia.Putting this all together yields, after some algebra.
$$\begin{eqnarray*} \frac{d\vec w}{dt}\approx -\frac{3GM_sat}{r_c^5} (x_csin\theta-y_ccos\theta)(x_c cos\theta+y_c sin\theta) \end{eqnarray*}$$
where $r_c$ is the distance from the center fo mass to Saturn

4 Main body

Source Code

5 Results

5.1 Results with different $dt$

First of all,We shall see the most general situation with the circular orbit.We plot $\theta$ versus time.With $dt$=0.0001 .However there is some disorder that should not exsist in this oribit orbit.So here we take this as a consequence of $dt$.

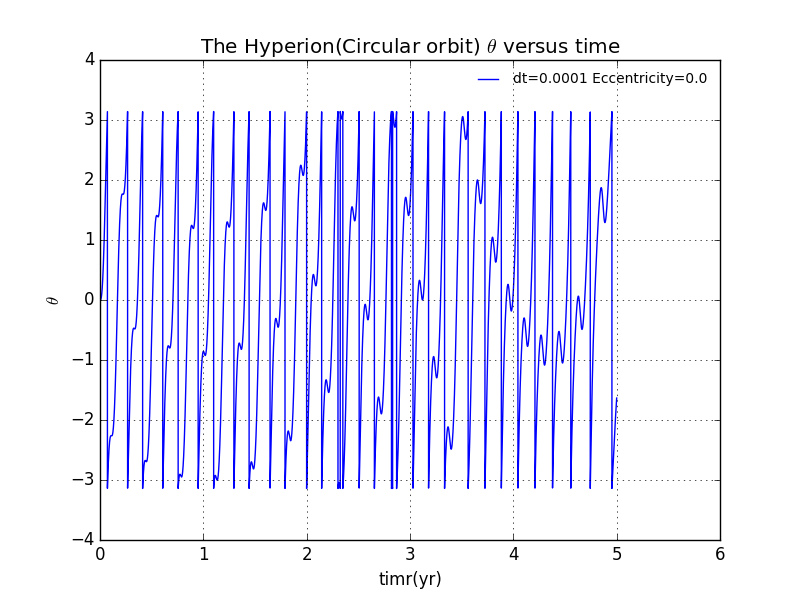
In the area closed by RED-LINE,we see obviously diorder of the plot.

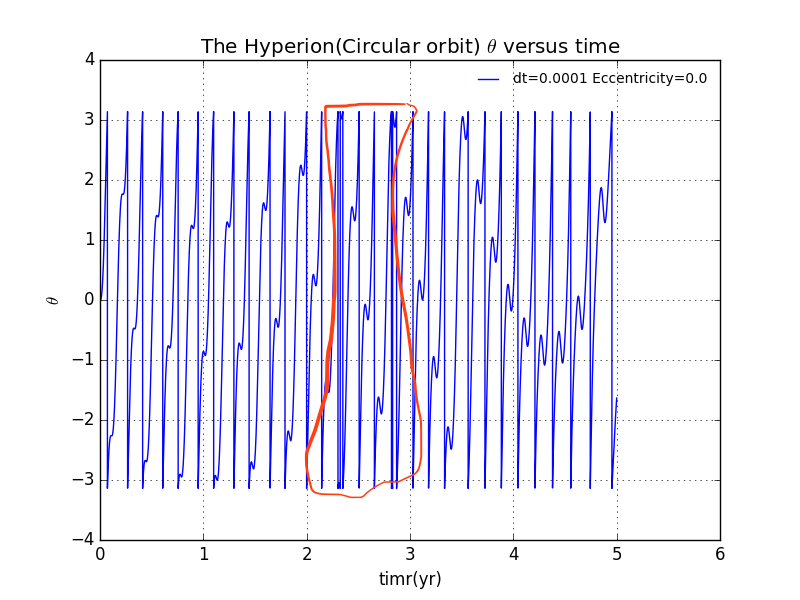
We take $dt$ to seperately be 0.0001,0.00001.

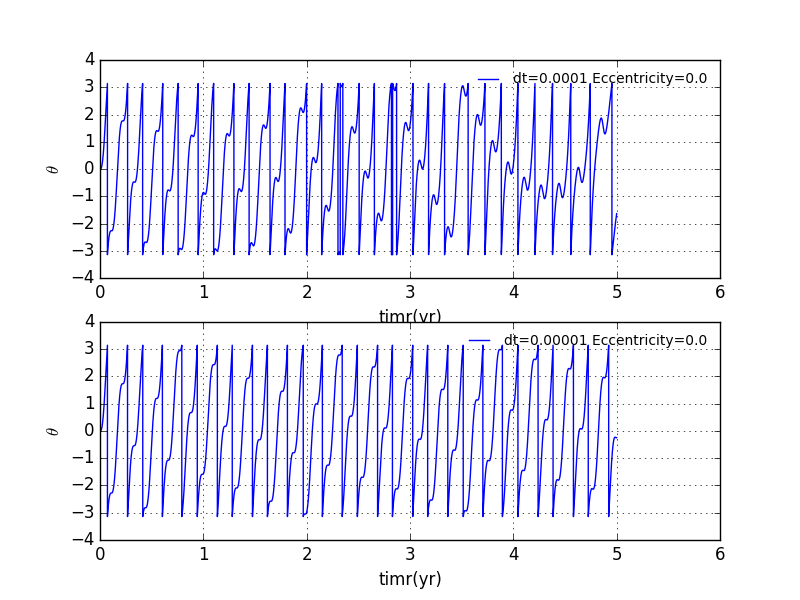
Now let us investigate situations with different $dt$,here we set $dt$ to seperately be 0.001,0.0005,0.0001,0.00001.It is evident that the disorder disappear with the increment of precision.With $dt$=0.0001,we barely see any disorder or chaos in the plot!

5.2 Results with single intial condition(circular).

Here it is an amplifying plot of $dt$=0.0001,as the precision is extremely high,the program take much longer time to process.In the later discussion,we shall use less precision with $dt$=0.001 without the interference of general results.

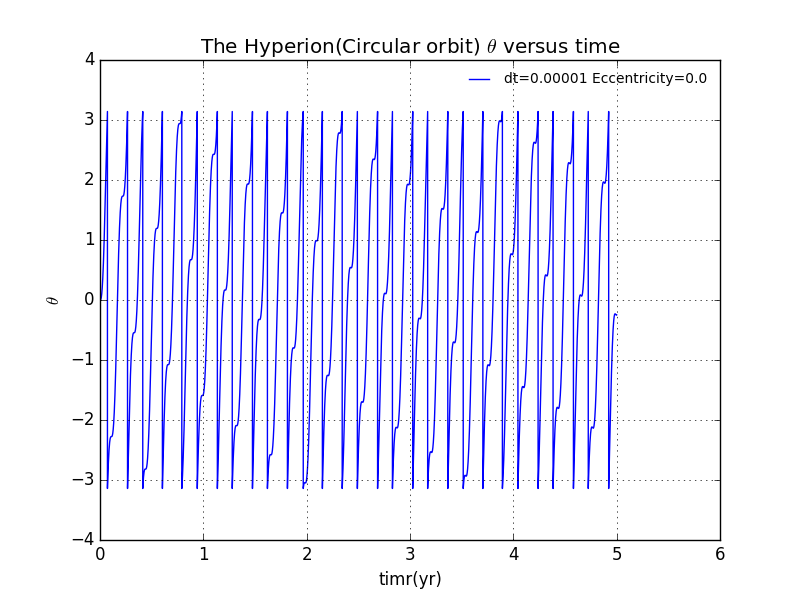
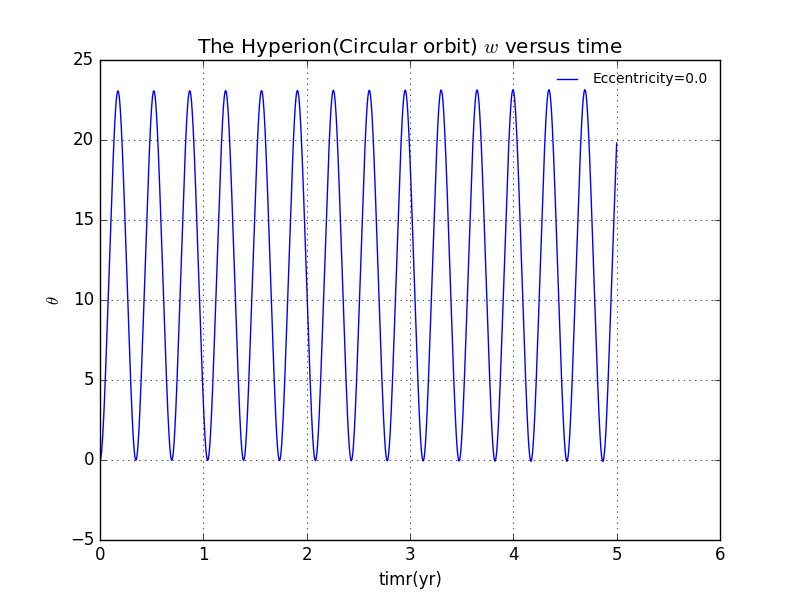
Let us take a better look at the behavior of $w$ versus time!Tumbling of Hyperion calculated assuming a circular orbit.It is eviedtly the $\theta$ as well as $w$ is periodic and not chaotic.The vertical jumps of the plot are due to the resetting of the angle from $+\pi$ to $-\pi$.

while self.sita[-1]>=1*math.pi:
                self.sita[-1]=self.sita[-1]-2*math.pi
while  self.sita[-1]<=-1*math.pi:
                self.sita[-1]=self.sita[-1]+2*math.pi

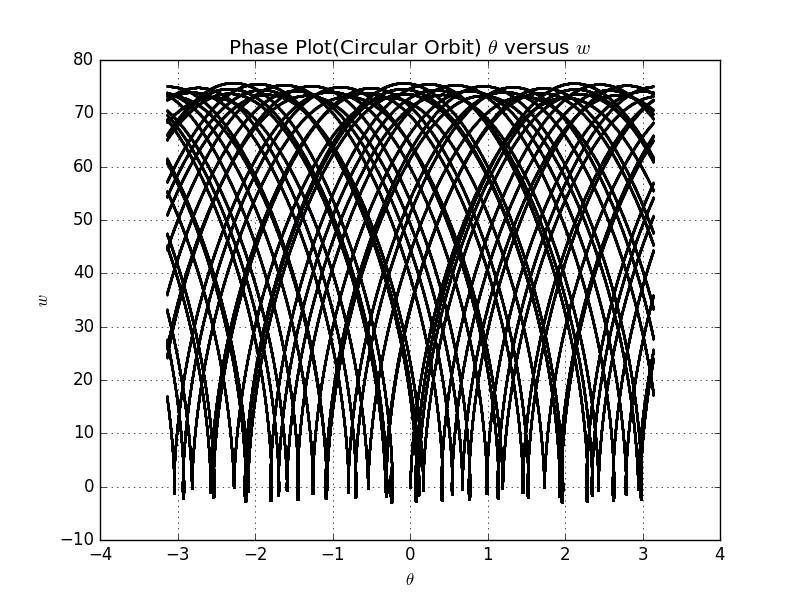
Additionally,we also draw the Phase Plot,which means plot with $w$ versue $\theta$.

5.3 Results with single intial condition(elleptical).

Assuming the orbit to be elleptical orbit.The tumbling of the Hyperion is now chaotic at different places of the plot

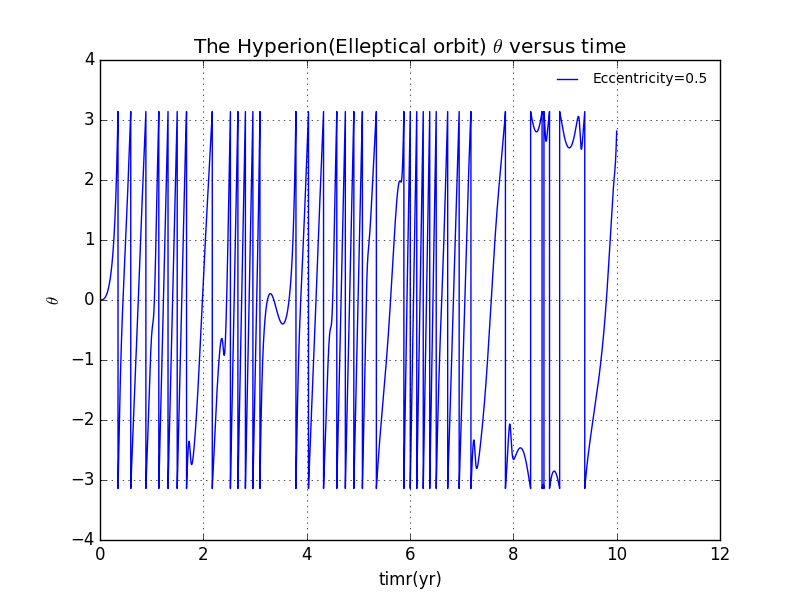
In the area of RED-LINE,there exhibit obviously chaos.

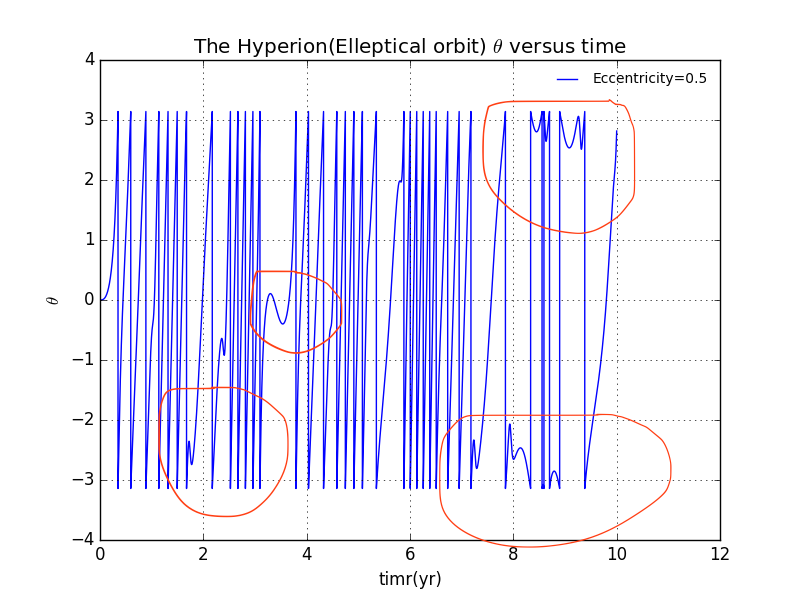
Now let us take a look of the $w$ versus time.It is surely chaotic too.

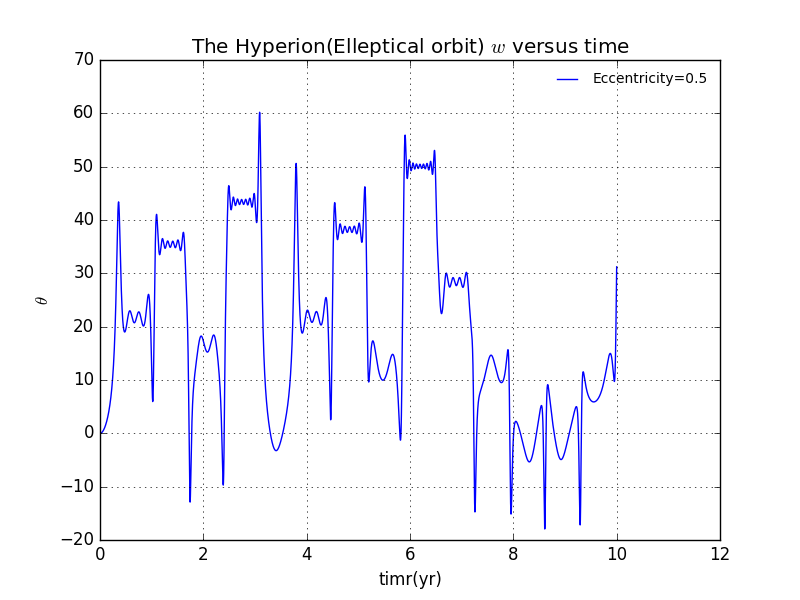
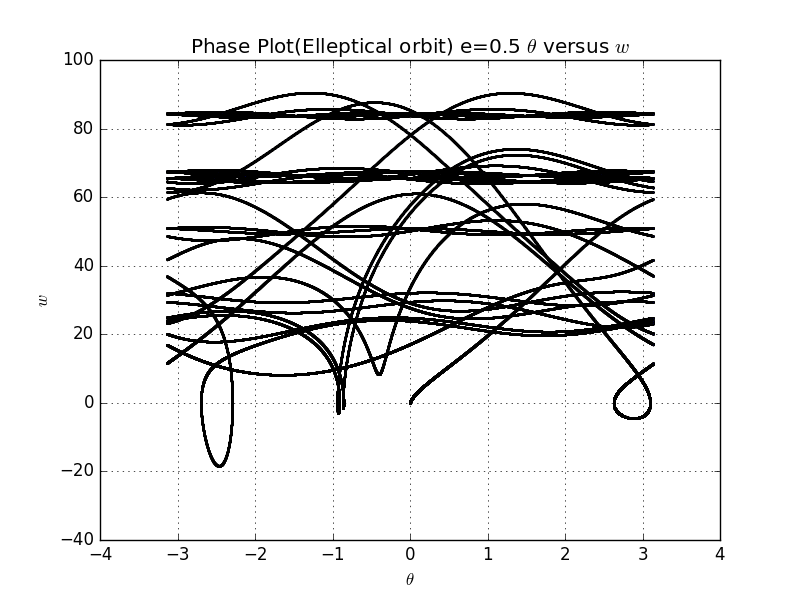
Additionally,we also draw the Phase Plot,which means plot with $w$ versue $\theta$. With expectiation ,the Phase Plot is fairly chaotic with elleptical orbit.

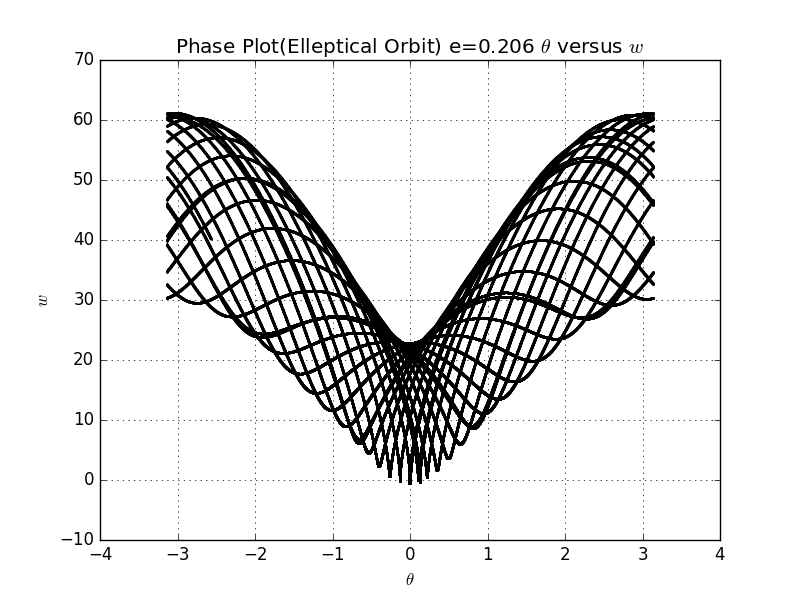
It is strange when the eccetrincity equals to 0.206,the phase plot becomes somehow periodic which is not what we expected before.

Here we observe the chaotic behavior versus different eccentricity.For the convenience of obervation we set $e$ to be 0.3,0.4,0.5,0.6.Progressively,the chaotic behavior is becoming more and more obviously as the increasing of eccerencity.

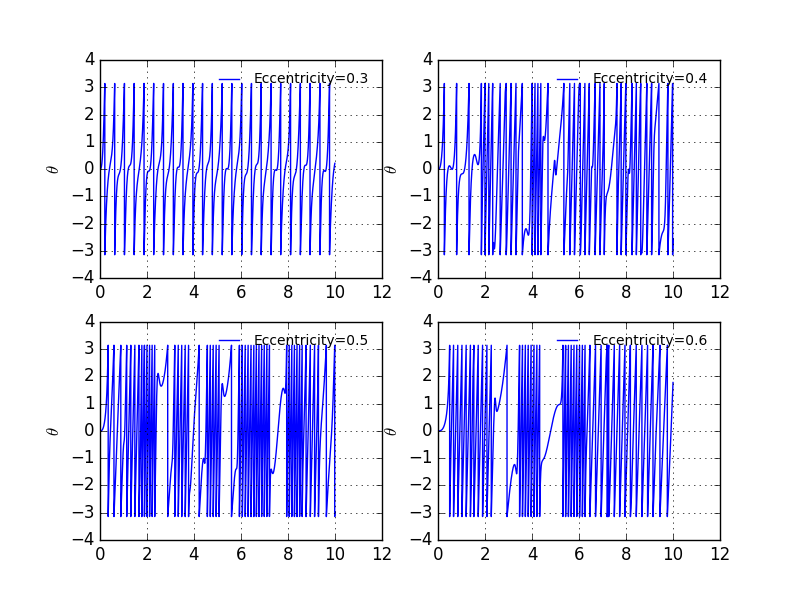
However,things are not as simple as you might have expected.The chaotic behavior is now seem to vanish with fairly large eccentricity.

5.3 Results with slightly varied intial conditions(Circular)

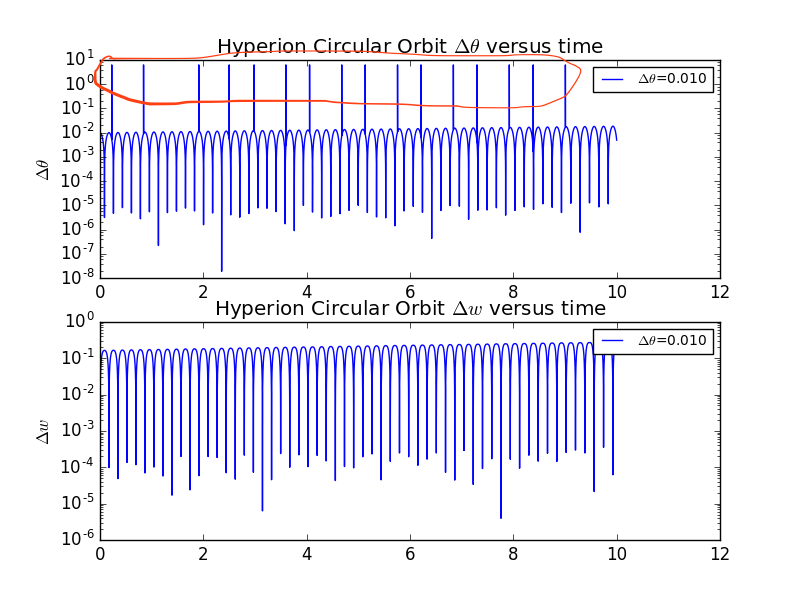
Here we consider the divergence of two nearby trajecotries of the tumbling motion of Hyperion.We plot the differnece between two calculated results fo $\theta$
with $\Delta \theta=0.01$.Noting that it being a circular orbit,we are not able to observe the chaotic in the plot.However,we found some strange points that interfered with periodic.

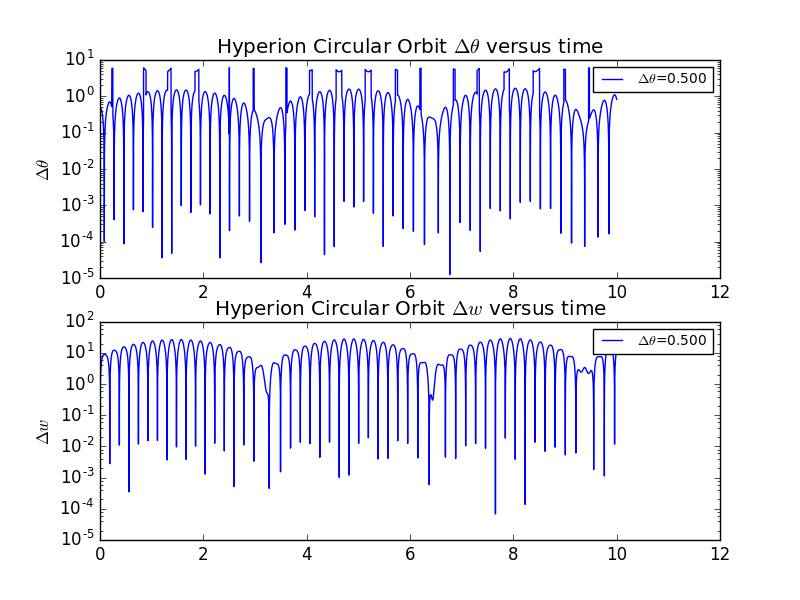
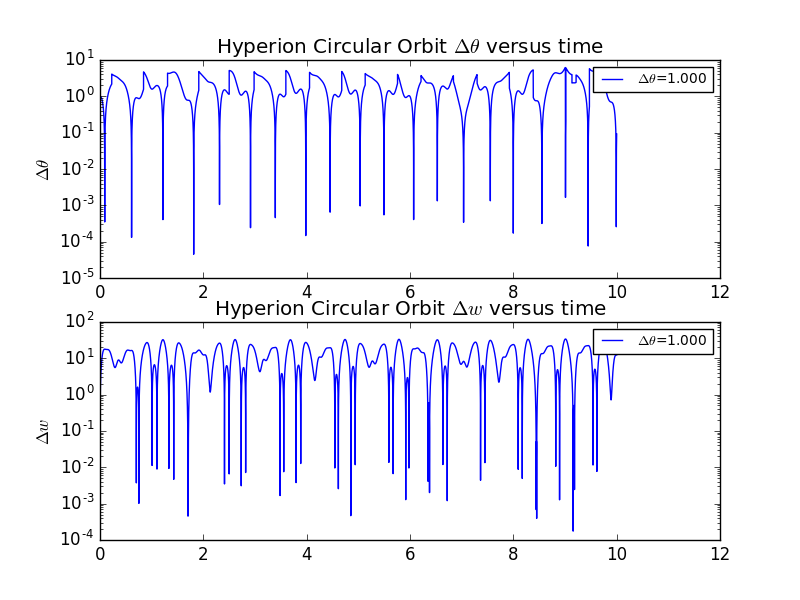
Now we also displays different situations with slightly different $\Delta \theta$=0.5 and 1.0.There is no obious chaos in both of them.

5.4 Results with slightly varied intial conditions(Elleptical)

Now let us investigat the chaotic situation.What is known to all is that the chaotic system is extrememly sensitive to the intial conditions.So we take a look what will happen with slight variation of $\theta$.We now set $\Delta \theta$=0.01.It is obvious that the divergence could becomes so large with time passing by.

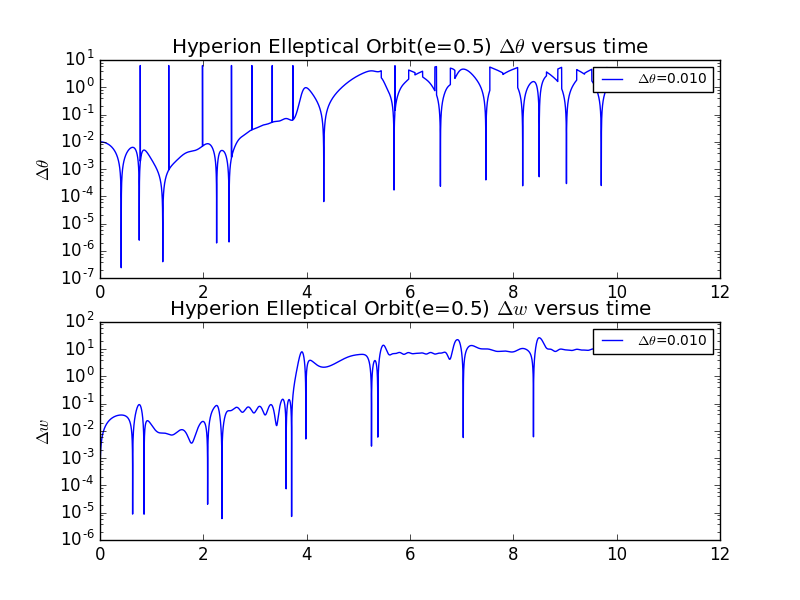
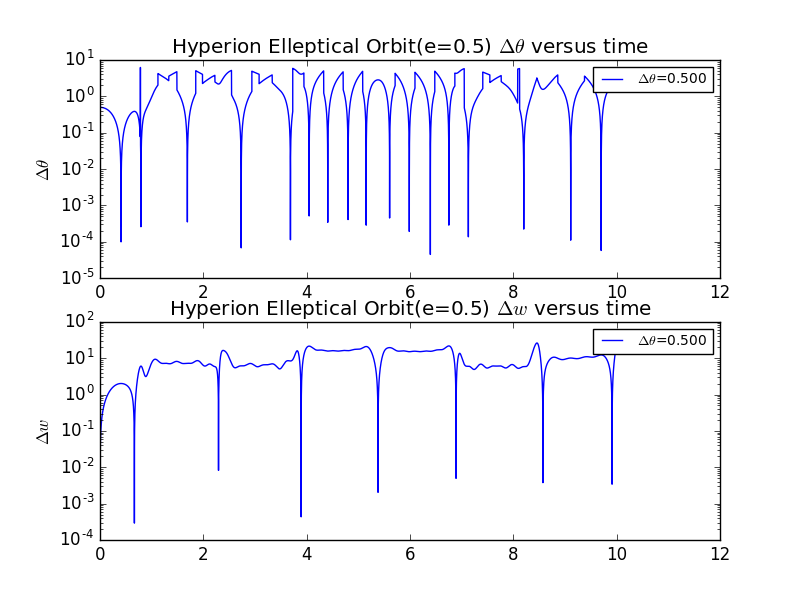
Now we also displays different situations with slightly different $\Delta \theta$=0.5 and 1.0.There is obious chaos in both of them.

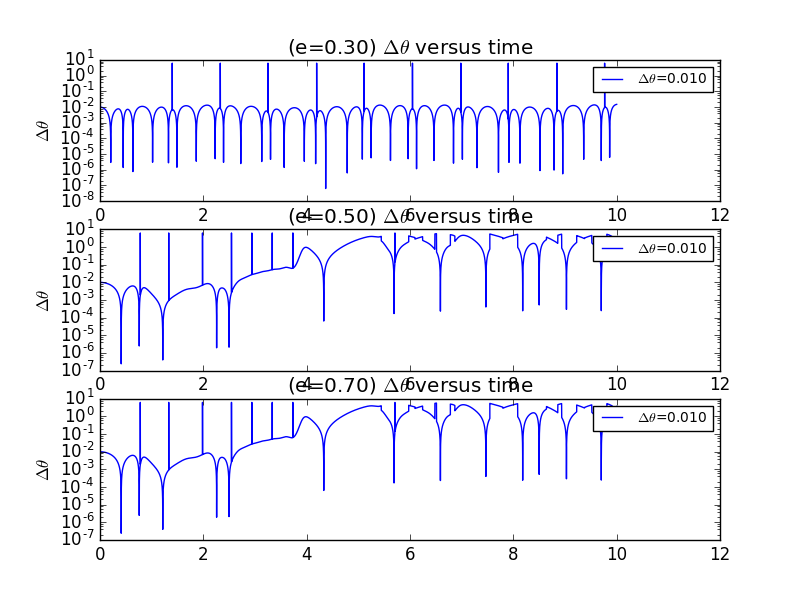
5.5 Results with different Eccentricity versus $\Delta \theta$

In problem 4.19,we are asked to investigate the behavior of the exponent varies as a function of the eccentricity.

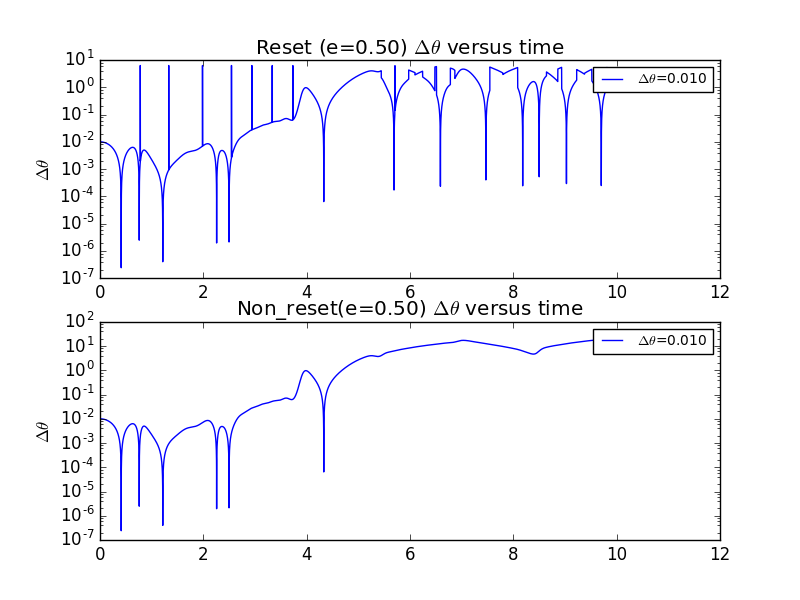
5.6 Results with Reset and Non-Reset.

In problem 4.20,we are asked to investigat the results betweem resetting the non-resetting the $\theta$.With non-resetting program,the vertical lines in the plot vanish.It is reasonable due to the fact that the 'sudden turning points vanish'.And the $\theta$ becomes a continuous vaiable versus time.

6 Acknowledemet

1.Wikipedia--the free encyclopedia.
2.Computational Physics,Nicholas J.Giordano,Hisao Nakanishi,the second edition,2006.